Ганопольский Родион Михайлович, к.ф.-м.н., зав. каф. МФПиС ФТИ
04.09.2017
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физико-математические аспекты нефтегазового дела. Прикладная физика презентация
Содержание
- 1. Физико-математические аспекты нефтегазового дела. Прикладная физика
- 2. Прикладная физика Содержание блока • Введение •
- 3. Введение
- 4. Введение • Основные обозначения • Системы измерений • Понятие «гидравлика» • Терминология
- 5. Система обозначений d— диаметр; Le— число
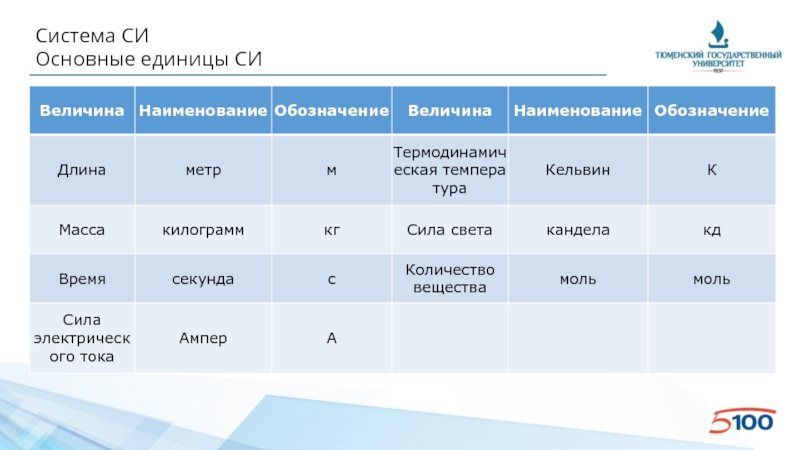
- 6. Система СИ Основные единицы СИ
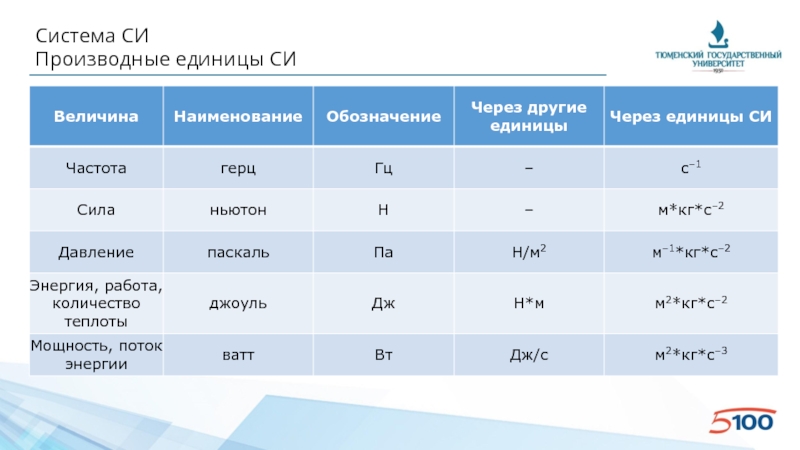
- 7. Система СИ Производные единицы СИ
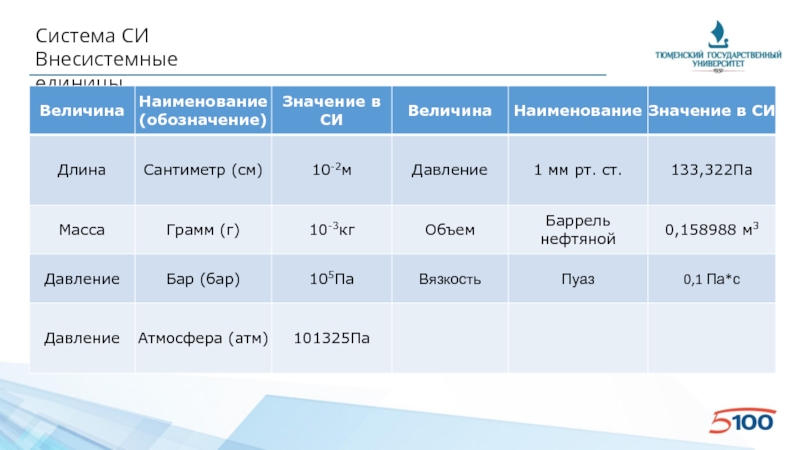
- 8. Система СИ Внесистемные единицы
- 9. Система СИ Английская система мер • Британская
- 10. Введение • Гидравлика - прикладная наука
- 11. Терминология Термодинамика • Термодинамическая фаза – гомогенная часть
- 12. Терминология Термодинамика • Гомогенная система содержит только одну
- 13. Терминология Гидравлика • Твердое тело – физическое тело
- 14. Свойства жидкостей и газов
- 15. Свойства жидкостей и газов • Механические
- 16. Механические свойства жидкостей • Плотность –
- 17. Термодинамические свойства жидкостей и газов Температура •
- 18. Термодинамические свойства жидкостей и газов Давление • Давление
- 19. Термодинамические свойства жидкостей и газов Удельная теплоемкость
- 20. Физические свойства жидкостей и газов Сжимаемость • Сжимаемость
- 21. Физические свойства жидкостей и газов Упругость • Упругость
- 22. Физические свойства жидкостей и газов Вязкость • Вязкость
- 23. Физические свойства жидкостей и газов Вязкость • Закон
- 24. Физические свойства жидкостей и газов Вязкость • Динамический
- 25. Физические свойства жидкостей и газов Вязкость • Распределение скоростей при течении вязкой жидкости вдоль стенки
- 26. Физические свойства жидкостей и газов Вязкость • Распределение скоростей при течении вязкой жидкости вдоль трубы
- 27. Физические свойства жидкостей и газов Вязкость • Распределение
- 28. Физические свойства жидкостей и газов Поверхностное натяжение
- 29. Физические свойства жидкостей и газов Поверхностное натяжение
- 30. Физические свойства жидкостей и газов Поверхностное натяжение.
- 31. Физические свойства жидкостей и газов Смачивание. Угол
- 32. Физические свойства жидкостей и газов Смачивание. Угол
- 33. Физические свойства жидкостей и газов Смачивание. Угол смачивания
- 34. Физические свойства жидкостей и газов Смачивание. Капиллярное явление
- 35. Физические свойства жидкостей и газов Растворимость газов
- 36. Физические свойства жидкостей и газов Растворимость газов в жидкостях
- 37. Физические свойства жидкостей и газов Испаряемость • Испаряемость
- 38. Физические свойства жидкостей и газов Кавитация • Кавитация
- 39. Физические свойства жидкостей и газов Кавитация
- 40. Идеальная и реальные жидкости • Идеальная жидкость
- 41. Измерение физических величин
- 42. Измерение физических величин Методы • Непосредственно прибором • Расчетные
- 43. Приборы для измерения физических величин Приборы • Термометр
- 44. Приборы для измерения физических величин Термометры • жидкостные • механические • электронные • оптические • инфракрасные • газовые
- 45. Приборы для измерения физических величин Термометры • жидкостные:
- 46. Приборы для измерения физических величин Термометры • оптические:
- 47. Приборы для измерения физических величин Барометры • Барометр —
- 48. Приборы для измерения физических величин Манометры • Манометр —
- 49. Приборы для измерения физических величин Весы и
- 50. Приборы для измерения физических величин Вискозиметры • Капиллярные • Ротационные • С падающим шариком • Пузырькового типа • Ультразвуковые
- 51. Приборы для измерения физических величин Вискозиметры • Капиллярные:
- 52. Приборы для измерения физических величин Вискозиметры • С
- 53. Приборы для измерения физических величин Ареометр • Основан
- 54. Приборы для измерения физических величин Расходомер • Расходомер —
- 55. Приборы для измерения физических величин Расходомеры, использующие
- 56. Приборы для измерения физических величин Расходомеры, использующие
- 57. Приборы для измерения физических величин Расходомеры, использующие
- 58. Приборы для измерения физических величин Расходомеры с
- 59. Приборы для измерения физических величин Расходомеры, основанные
- 60. Приборы для измерения физических величин Расходомеры, основанные
- 61. Расчётные методы измерения физических величин Пример 1
- 62. Расчётные методы измерения физических величин Пример 1.
- 63. Расчётные методы измерения физических величин Пример 2
- 64. Расчётные методы измерения физических величин Пример 2.
- 65. Гидростатика
- 66. Гидростатика • Гидростатическое давление • Основное уравнение гидростатики
- 67. Гидростатика • На жидкость, находящуюся в состоянии
- 68. Гидростатика Гидростатическое давление • Основное понятие гидростатики –
- 69. Гидростатика Гидростатическое давление • Гидростатическое давление направлено всегда
- 70. Гидростатика Основное уравнение гидростатики • X, Y, Z
- 71. Гидростатика Поверхность уровня • Поверхность уровня – поверхность
- 72. Гидростатика Давление при абсолютном покое • В состоянии
- 73. Гидростатика Анализ основного уравнения гидростатики • Гидростатическое давление
- 74. Гидростатика Условия равновесия • Открытый сосуд h =
- 75. Гидростатика Сообщающиеся сосуды с 2 жидкостями • В
- 76. Гидростатика Пример 1 • Определить абсолютное и
- 77. Гидростатика Пример 1 • Согласно основному уравнению
- 78. Гидростатика Пример 2 • Определить давление p0
- 79. Гидростатика Пример 2 • Условие равновесия для
- 80. Гидростатика Задача 1 • Определить избыточное давление
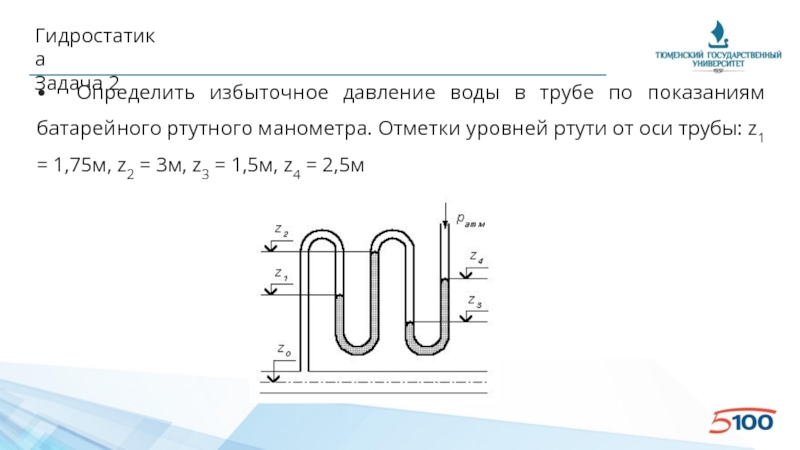
- 81. Гидростатика Задача 2 • Определить избыточное давление
- 82. Гидростатика Закон Паскаля • Давление, производимое на
- 83. Гидростатика Давление на стенки сосуда • Объединяем закон
- 84. Гидростатика Закон Архимеда • На тело, погружённое
- 85. Гидростатика Условия плавания тел • FA <
- 86. Гидростатика Равновесие плавающего тела • Для однородного
- 87. Гидростатика Примеры расчётов • Определить, будет ли
- 88. Гидростатика Примеры расчётов • Полый железный шар
- 89. Гидростатика Примеры расчётов • 1600 кг/м3 • 2,1*10-5 м3
- 90. Течение жидкости в трубопроводе
- 91. Течение жидкости в трубопроводе • Режимы течения
- 92. Течение жидкости в трубопроводе Режимы течения жидкости
- 93. Течение жидкости в трубопроводе Число Рейнольдса • В
- 94. Течение жидкости в трубопроводе Число Рейнольдса
- 95. Течение жидкости в трубопроводе Примеры • По трубопроводу
- 96. Течение жидкости в трубопроводе Пример
- 97. Течение жидкости в трубопроводе Примеры • Для
- 98. Течение жидкости в трубопроводе Уравнение непрерывности ∇ — дивергенция,
- 99. Течение жидкости в трубопроводе Уравнение сохранения • Если q — сохраняющаяся
- 100. Течение жидкости в трубопроводе Примеры • На
- 101. Течение жидкости в трубопроводе Примеры • Азот
- 102. Течение жидкости в трубопроводе Кинематика жидкости •
- 103. Течение жидкости в трубопроводе Характер движения жидкости
- 104. Течение жидкости в трубопроводе Трубка тока •
- 105. Течение жидкости в трубопроводе Расход. Уравнение расхода
- 106. Течение жидкости в трубопроводе Потоки жидкости • Потоком
- 107. Течение жидкости в трубопроводе Гидравлические элементы потока
- 108. Течение жидкости в трубопроводе Динамика жидкости • Уравнение Бернулли • Измерение расходов и скоростей жидкости • Примеры расчётов
- 109. Течение жидкости в трубопроводе Уравнение Бернулли • Уравнение
- 110. Течение жидкости в трубопроводе Энергетическая интерпретация уравнения
- 111. Течение жидкости в трубопроводе Уравнение Бернулли для
- 112. Течение жидкости в трубопроводе Уравнение Бернулли для
- 113. Течение жидкости в трубопроводе Уравнение Бернулли. Напорная
- 114. Течение жидкости в трубопроводе Измерение расходов и
- 115. Течение жидкости в трубопроводе Измерение расходов и
- 116. Течение жидкости в трубопроводе Уравнение Бернулли. Пример
- 117. Течение жидкости в трубопроводе Уравнение Бернулли. Пример.
- 118. Течение жидкости в трубопроводе Уравнение Бернулли. Пример
- 119. Течение жидкости в трубопроводе Уравнение Бернулли. Пример. Решение
- 120. Течение жидкости в трубопроводе Методы Эйлера и
- 121. Течение жидкости в трубопроводе Уравнения Эйлера для
- 122. Течение жидкости в трубопроводе Уравнения Эйлера для
- 123. Течение жидкости в трубопроводе Метод Лагранжа • Рассматривается
- 124. Течение жидкости в трубопроводе Уравнения Навье-Стокса • В
- 125. Течение жидкости в трубопроводе Уравнения Навье-Стокса •
- 126. Течение жидкости в трубопроводе Уравнения Навье-Стокса. Основные
- 127. Неньютоновские и высоковязкие жидкости
- 128. Неньютоновские жидкости • Неньютоновская жидкость - жидкость, при
- 129. Высоковязкие жидкости • Особый вид транспортировки, специальные устройства для смешивания.
- 130. Высоковязкие жидкости • Особый вид транспортировки, специальные устройства для смешивания.
- 131. Структура многофазного потока
- 132. Структура многофазного потока • Многофазные потоки возникают
- 133. Структура многофазного потока Режимы многофазного потока • Пузырьковое
- 134. Структура многофазного потока Режимы многофазного потока • Снарядный
- 135. Структура многофазного потока Режимы многофазного потока •
- 136. Структура многофазного потока Режимы многофазного потока •
- 137. Структура многофазного потока Карта Тайтеля-Даклера • Карта Тайтеля-Даклера
Слайд 1Программа «Концептуальный инжиниринг месторождений нефти и газа»
Курс «Физико-математические аспекты нефтегазового дела»
Блок
Слайд 2Прикладная физика
Содержание блока
• Введение
• Свойства жидкостей и газов
• Измерение физических величин
•
• Течение жидкости в трубопроводе
• Высоковязкие жидкости
• Структура многофазного потока
Слайд 5Система обозначений
d— диаметр;
Le— число Льюиса;
М— число Маха;
m —масса жидкости;
Nu— число Нуссельта;
п — показатель
Pr— число Прандтля;
р — давление;
q— скоростной напор;
Re— число Рейнольдса;
Т — температура;
t— время;
и — составляющая вектора скорости в направлении течения;
η — коэффициент динамической вязкости;
V — объем жидкости;
ν — коэффициент кинематической вязкости;
ρ — плотность жидкости или газа;
γ — удельный вес
Слайд 9Система СИ
Английская система мер
• Британская имперская система
1 баррель для сырой нефти
1 тонна большая (длинная) (long ton) = 2240 фунтов = 1016,05 кг
1 морская миля (nautical mile) = 10 кабельтовым = 1,853256 км
1 акр (acre) = 4 рудам = 4046,86 м²
• Американская система мер
1 баррель для сырой нефти = 42,2 галлонов = 158,97 л (дм³)
1 морская миля = 1,852 км
Слайд 10Введение
• Гидравлика - прикладная наука о законах движения, равновесии жидкостей и
физические свойства жидкостей и газов
гидростатика
гидродинамика
кинематическая гидравлика
примеры практического применения
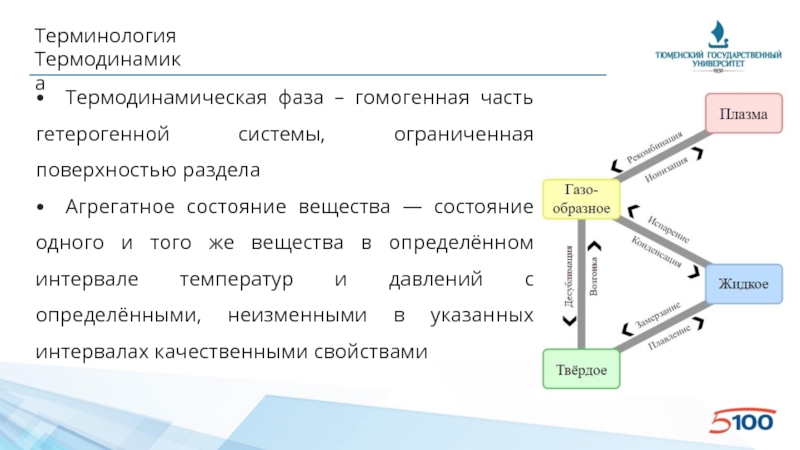
Слайд 11Терминология
Термодинамика
• Термодинамическая фаза – гомогенная часть гетерогенной системы, ограниченная поверхностью раздела
• Агрегатное состояние
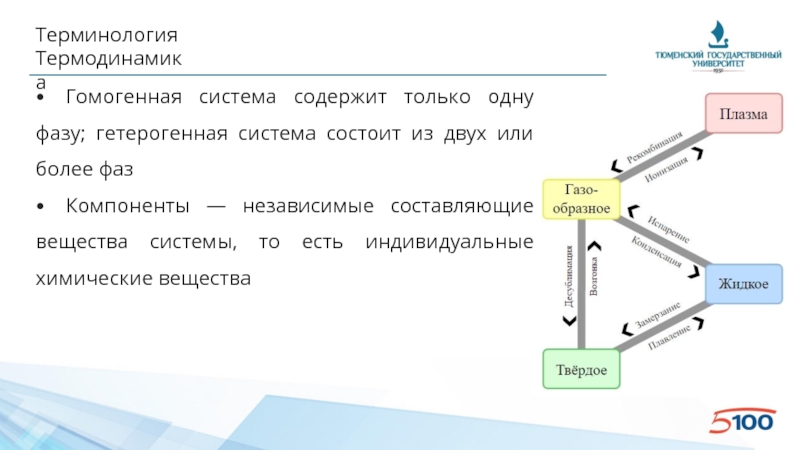
Слайд 12Терминология
Термодинамика
• Гомогенная система содержит только одну фазу; гетерогенная система состоит из двух
• Компоненты — независимые составляющие вещества системы, то есть индивидуальные химические вещества
Слайд 13Терминология
Гидравлика
• Твердое тело – физическое тело со стабильной формой и атомами, совершающими
• Жидкость – физическое тело, не обладающее способностью сохранять свою форму из-за слабой связи между отдельными его частицами. Жидкость принимает форму того сосуда, в котором находится
• Газ – занимает весь предоставленный объем
• К гидромеханике относят жидкие тела и газообразные тела
Слайд 15Свойства жидкостей и газов
• Механические свойства жидкостей и газов
- плотность и
• Термодинамические свойства
- теплоемкость, температура, давление
• Физические свойства
- упругость, сжимаемость, вязкость, поверхностное натяжение, смачивание, растворимость
Слайд 16Механические свойства жидкостей
• Плотность – отношение массы тела к занимаемому этим
• Удельный вес – вес жидкости, приходящийся на единицу объема (Н/м3)
Слайд 17Термодинамические свойства жидкостей и газов
Температура
• Температура – физическая величина, характеризующая термодинамическую
• Обозначение – T (К)
Тс = Т – 273.15К
• 0°С – 273,15К
Слайд 18Термодинамические свойства жидкостей и газов
Давление
• Давление — физическая величина, численно равная силе,
p = ∆F/ ∆S
• Давление газа
Слайд 19Термодинамические свойства жидкостей и газов
Удельная теплоемкость
• Количество теплоты, которое поглощается или
• c – удельная теплоемкость материала
Слайд 20Физические свойства жидкостей и газов
Сжимаемость
• Сжимаемость – свойство жидкостей и газов изменять
Слайд 21Физические свойства жидкостей и газов
Упругость
• Упругость – это способность газа принимать свой
E = 1/β
Слайд 22Физические свойства жидкостей и газов
Вязкость
• Вязкость - свойство жидкости сопротивляться сдвигу или
Слайд 23Физические свойства жидкостей и газов
Вязкость
• Закон Ньютона-Петрова:
τ – сила внутреннего трения слоев
η – динамический коэффициент вязкости
S – площадь соприкасающихся слоев
∆U – разность скоростей двух соседних слоев жидкости, расположенных на расстоянии ∆n друг от друга по нормали
Слайд 24Физические свойства жидкостей и газов
Вязкость
• Динамический коэффициент вязкости
• Кинематическая вязкость - в размерность
ν=η/ρ
• Ньютоновские жидкости - жидкости, для которых справедлив закон Ньютона
• Неньютоновские жидкости - кефир, сметана, сгущенное молоко, томатные пасты
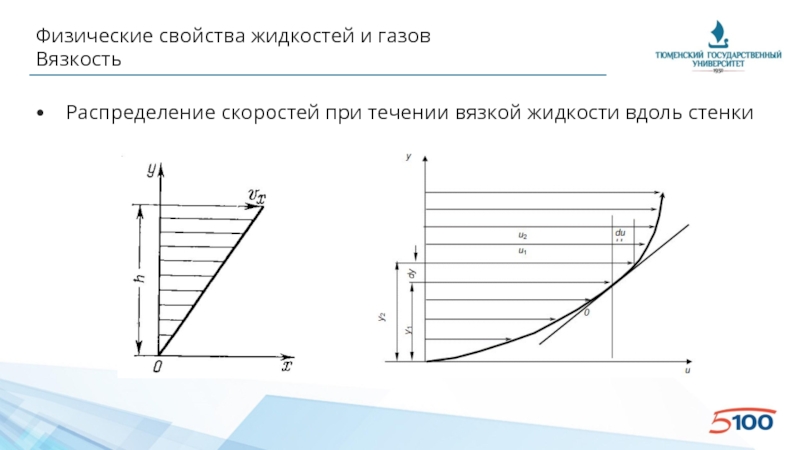
Слайд 25Физические свойства жидкостей и газов
Вязкость
• Распределение скоростей при течении вязкой жидкости вдоль
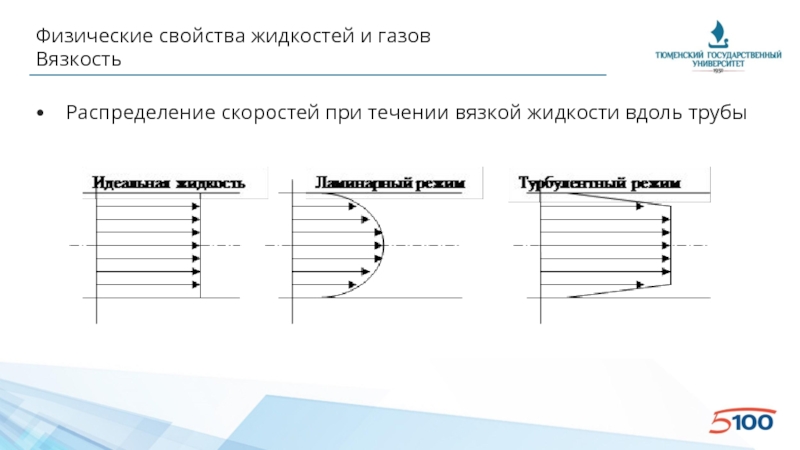
Слайд 26Физические свойства жидкостей и газов
Вязкость
• Распределение скоростей при течении вязкой жидкости вдоль
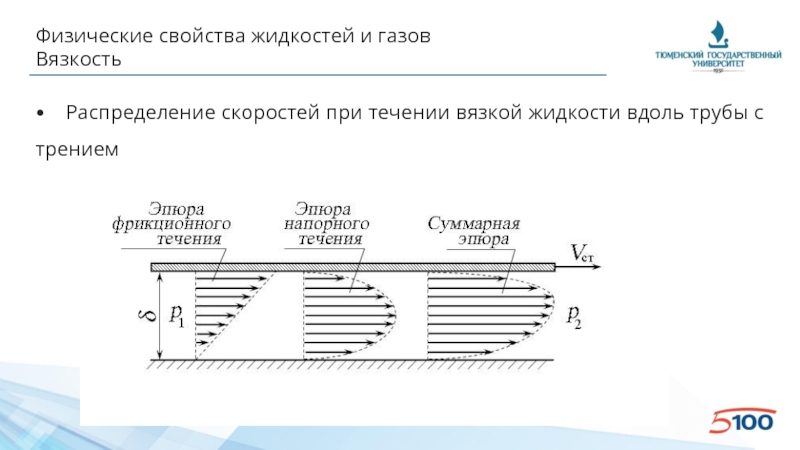
Слайд 27Физические свойства жидкостей и газов
Вязкость
• Распределение скоростей при течении вязкой жидкости вдоль
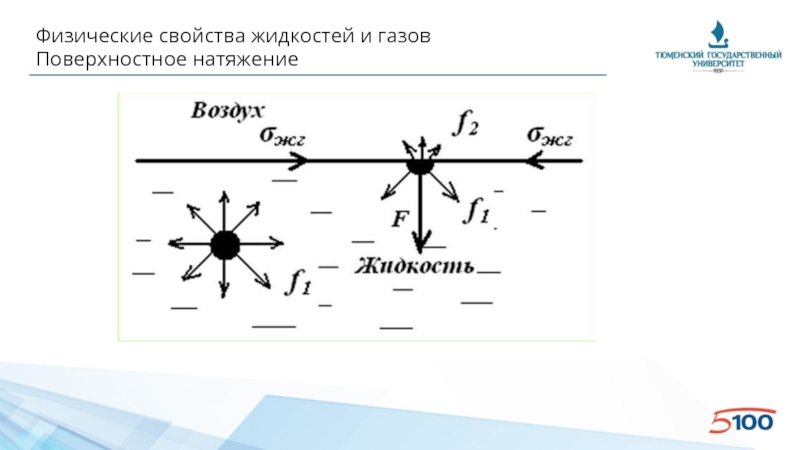
Слайд 29Физические свойства жидкостей и газов
Поверхностное натяжение
• Система, находящаяся в равновесии, занимает положение,
• Силы поверхностного натяжения – силы, направленные по касательной
σ = -R/L
L - длина линии, ограничивающая поверхность раздела.
• Коэффициент поверхностного натяжения
• Дополнительное давление (формула Лапласа)
ρ=σ/(1/R1+1/R2)
Слайд 30Физические свойства жидкостей и газов
Поверхностное натяжение. Проявления
• В невесомости капля принимает сферическую
• Струя воды «сливается» в цилиндр, который затем разбивается на шаровидные капли
• Маленькие объекты с плотностью, большей плотности жидкости, способны «плавать» на поверхности жидкости
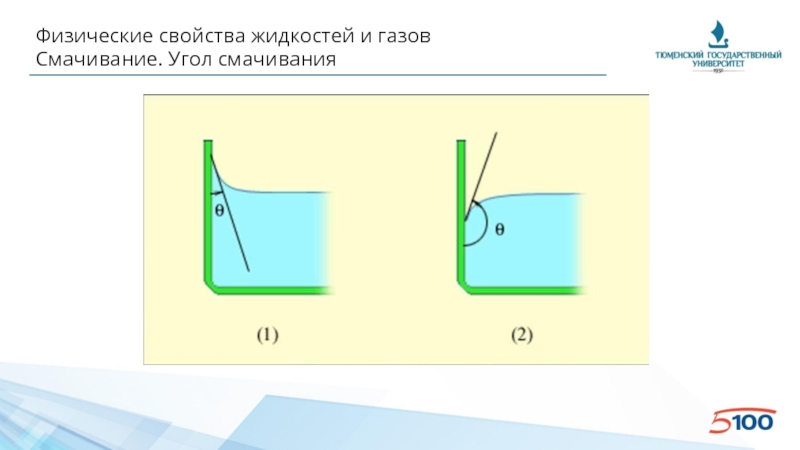
Слайд 31Физические свойства жидкостей и газов
Смачивание. Угол смачивания
• Смачивание — физическое взаимодействие жидкости с поверхностью твёрдого тела или
• Полное несмачивание
• Частичное несмачивание
• Частичное смачивание
• Полное смачивание
Слайд 32Физические свойства жидкостей и газов
Смачивание. Угол смачивания
• Смачивание зависит от соотношения между
• Молекулы жидкости притягиваются друг к другу сильнее, чем к молекулам твёрдого тела – несмачивание
• Молекулы жидкости притягиваются друг к другу слабее, чем к молекулам твёрдого тела – смачивание
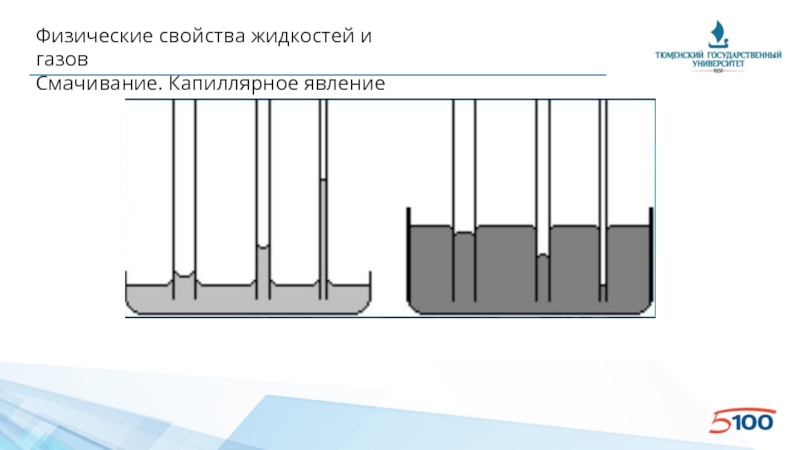
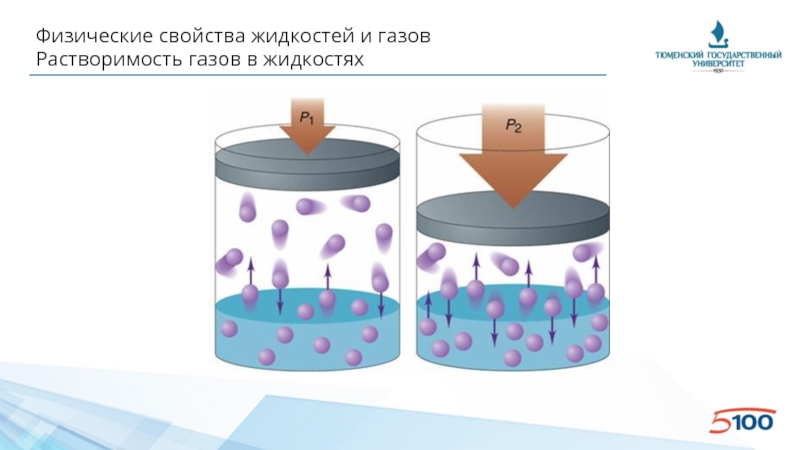
Слайд 35Физические свойства жидкостей и газов
Растворимость газов в жидкостях
• Растворимость газа в жидкости
• Закон Генри: растворимость газа пропорциональна его давлению
• При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Выделиться газ может в считанные секунды или даже доли секунды
Слайд 37Физические свойства жидкостей и газов
Испаряемость
• Испаряемость – свойство капельных жидкостей превращаться в
• Интенсивное парообразование по всему объему — кипение жидкости
• Свойство имеет как положительные, так и отрицательные стороны
Положительное - это возможность из нефти получать различные фракции и множество нефтепродуктов и сырья для химической промышленности; способность полного сгорания нефтепродуктов в ДВС, турбинах, котельных установок
Отрицательное - теряется большое количество нефти (до 10—12% в год от объема добычи)
Слайд 38Физические свойства жидкостей и газов
Кавитация
• Кавитация – местное нарушение сплошности течения жидкости
• Процесс парообразования и последующего схлопывания пузырьков пара с одновременным конденсированием пара в потоке жидкости
Слайд 40Идеальная и реальные жидкости
• Идеальная жидкость – это абсолютно несжимаемая, абсолютно невязкая
• Реальные жидкости обладают сжимаемостью, вязкостью и теплопроводностью, однако решение ряда теоретических вопросов в гидравлике значительно облегчается при использовании идеальной жидкости
Слайд 42Измерение физических величин
Методы
• Непосредственно прибором
• Расчетные – с помощью формул на основании измеренных
Слайд 43Приборы для измерения физических величин
Приборы
• Термометр - температура
• Барометр и манометр – давление
• Весы
• Динамометр – сила
• Психрометр – относительная влажность воздуха
• Вискозиметр – вязкость
• Ареометр – плотность жидкостей
• Расходомер – расход вещества
Слайд 44Приборы для измерения физических величин
Термометры
• жидкостные
• механические
• электронные
• оптические
• инфракрасные
• газовые
Слайд 45Приборы для измерения физических величин
Термометры
• жидкостные: основаны на принципе изменения объёма жидкости,
• механические: действуют по тому же принципу, что и жидкостные, но в качестве датчика обычно используется металлическая спираль или лента из биметалла
• электронные: принцип основан на изменении сопротивления проводника при изменении температуры окружающей среды
Слайд 46Приборы для измерения физических величин
Термометры
• оптические: позволяют регистрировать температуру благодаря изменению уровня светимости, спектра и
• газовые: основаны на законе Шарля (p~T при V=const)
Слайд 47Приборы для измерения физических величин
Барометры
• Барометр — прибор для измерения атмосферного давления
• Барометры делятся на
в жидкостных барометрах давление измеряется высотой столба жидкости
крышка коробочки, к которой прикреплена пружина с передающим механизмом, деформируется, из-за чего стрелка на шкале показывает соответствующие данные
Слайд 48Приборы для измерения физических величин
Манометры
• Манометр — прибор, измеряющий давление жидкости или газа
• Манометр делятся
• Механическое измерение давления основывается на эластичном измерительном элементе, способном под воздействием сжимающей нагрузки деформироваться строго определенным образом и испытанную деформацию воспроизводить
Слайд 49Приборы для измерения физических величин
Весы и динамометр
• Механические динамометры (рычажные и пружинные),
• Два вида механических динамометров: пружинный и рычажный
• Действие гидравлического динамометра основано на вымещении измеряемой силой жидкости из цилиндра
• Электрический динамометр состоит из датчика, который преобразует деформацию от воздействия силы в электрический сигнал
Слайд 50Приборы для измерения физических величин
Вискозиметры
• Капиллярные
• Ротационные
• С падающим шариком
• Пузырькового типа
• Ультразвуковые
Слайд 51Приборы для измерения физических величин
Вискозиметры
• Капиллярные: основаны на подсчёте времени протекания заданного
• Ротационные: два тела вращения, одинаковых или разных, совмещаются по осям так, что одно из них прикасается изнутри к другому. Пространство между телами заполняют исследуемым веществом, и к одному из тел подаётся крутящий момент
Слайд 52Приборы для измерения физических величин
Вискозиметры
• С падающим шариком: определяется по времени прохождения
• Пузырькового типа: основан на определении параметров движения пузырька газа, свободно всплывающего в вязкой среде
• Ультразвуковые: изменение резонансной частоты колебаний в жидкости различной вязкости
Слайд 53Приборы для измерения физических величин
Ареометр
• Основан на законе Архимеда
• Плотность жидкостей сильно зависит
• Для практического применения ареометр градуируют в концентрации растворенного вещества, например, спиртомер
Слайд 54Приборы для измерения физических величин
Расходомер
• Расходомер — прибор, измеряющий количество вещества (объем, масса),
• Делятся на:
использующие гидродинамические методы
с непрерывно движущимся телом
основанные на различных физических явлениях
основанные на особых методах
Слайд 55Приборы для измерения физических величин
Расходомеры, использующие гидродинамические методы
• Парциальные расходомеры
• Расходомеры переменного давления
• Расходомер
• Расходомеры обтекания
• Вихревые расходомеры
Слайд 56Приборы для измерения физических величин
Расходомеры, использующие гидродинамические методы
• Расходомеры переменного давления: измеряют
• Расходомер переменного уровня: в основе работы лежит зависимость между расходом жидкости и высотой ее уровня в сосуде, при этом жидкость должна постоянно поступать в сосуд и вытекать через небольшое отверстие
• Расходомеры обтекания: чувствительный элемент воспринимает динамическое давление потока и перемещается под его воздействием
Слайд 57Приборы для измерения физических величин
Расходомеры, использующие гидродинамические методы
• Вихревые расходомеры: расход зависит
• Парциальные расходомеры: расход вещества определяется через некоторую долю основного потока в небольшой трубе, подключенной параллельно к основному трубопроводу
Слайд 58Приборы для измерения физических величин
Расходомеры с непрерывно движущимся телом
• Камерные счетчики и
• Силовые расходомеры: основанные на зависимости от массового расхода эффекта силового воздействия, сообщающего потоку ускорение того или другого рода (какая сила или мощность требуются)
• Тахометрические-расходомеры: имеют подвижный, обычно вращающийся элемент, скорость движения которого пропорциональна объемному расходу
Слайд 59Приборы для измерения физических величин
Расходомеры, основанные на различных физических явлениях
• Акустические расходомеры
• Ионизационные
• Оптические расходомеры
• Тепловые расходомеры
• Электромагнитные расходомеры
• Ядерно-магнитные расходомеры
Слайд 60Приборы для измерения физических величин
Расходомеры, основанные на особых методах
• Концентрационные расходомеры
• Корреляционные расходомеры
• Меточные
• Расходомеры с автоколеблющимся телом
• Расходомеры с подвижным участком трубопровода
• Струйные расходомеры
Слайд 61Расчётные методы измерения физических величин
Пример 1
• Сосуд заполнен водой, занимающей объем V1=2м³. При
Слайд 62Расчётные методы измерения физических величин
Пример 1. Решение
• Изменение объема
∆V = V2
• Увеличение давления ∆p=200 бар=2*107 Па
• Коэффициент объемного сжатия
β = ∆V/V/∆p = 4,74*10-10 1/Па
• Модуль объемной упругости
E = 1/β = 2,11*109 Па
Слайд 63Расчётные методы измерения физических величин
Пример 2
• Определить коэффициент динамической и кинематической вязкости
Слайд 64Расчётные методы измерения физических величин
Пример 2. Решение
• Сила сопротивления определяется по формуле
F = 3*π*μ*u*d
• Вес шарика
G = ρ*g*π*d3/6
• Скорость постоянна, значит, F = G
3*π*μ*u*d = ρ*g*π*d3/6
μ = ρ*g*d2/18/u = 0,008 Па*с
• Коэффициент кинематической вязкости
ν=μ/ρ=8*10-6м2/с
Слайд 66Гидростатика
• Гидростатическое давление
• Основное уравнение гидростатики
• Давление на стенки сосуда
• Законы Паскаля и Архимеда
• Примеры расчётов
Слайд 67Гидростатика
• На жидкость, находящуюся в состоянии покоя, действуют силы, которые можно разделить
• Поверхностные силы приложены к частицам жидкости, находящимся на поверхности раздела данной жидкости и другой среды
• Массовые силы воздействуют на все частицы данного объема жидкости и пропорциональны массе каждой частицы
• Основное понятие гидростатики – гидростатическое давление
Слайд 68Гидростатика
Гидростатическое давление
• Основное понятие гидростатики – гидростатическое давление
Слайд 69Гидростатика
Гидростатическое давление
• Гидростатическое давление направлено всегда по внутренней нормали к площадке, на
• Величина гидростатического давления в любой точке жидкости по всем направлениям одинакова
• Различают давление абсолютное (полное) и избыточное
Слайд 70Гидростатика
Основное уравнение гидростатики
• X, Y, Z – проекции единичных массовых сил на
Слайд 71Гидростатика
Поверхность уровня
• Поверхность уровня – поверхность равного давления
• Две поверхности уровня не пересекаются
• Массовые силы направлены нормально к поверхности уровня
• Поверхность уровня на границе жидкой и газообразной среды называется свободной поверхностью
Слайд 72Гидростатика
Давление при абсолютном покое
• В состоянии абсолютного покоя под действием сил тяжести
X = 0; Y = 0; Z = -g
dp = -ρ*g*dz
p = p0 + ρ*g*h
• Основное уравнение гидростатики
• Поверхность уровня (и свободная поверхность) при абсолютном покое – горизонтальная плоскость
z = const
Слайд 73Гидростатика
Анализ основного уравнения гидростатики
• Гидростатическое давление p есть сумма внешнего давления p0,
• Внешнее давление передается во все точки покоящейся жидкости без изменения, поэтому жидкость используется как среда для передачи давления (гидравлические машины) – закон Паскаля
• Поверхность уровня (и свободная поверхность) при абсолютном покое – горизонтальная плоскость
z = const
Слайд 74Гидростатика
Условия равновесия
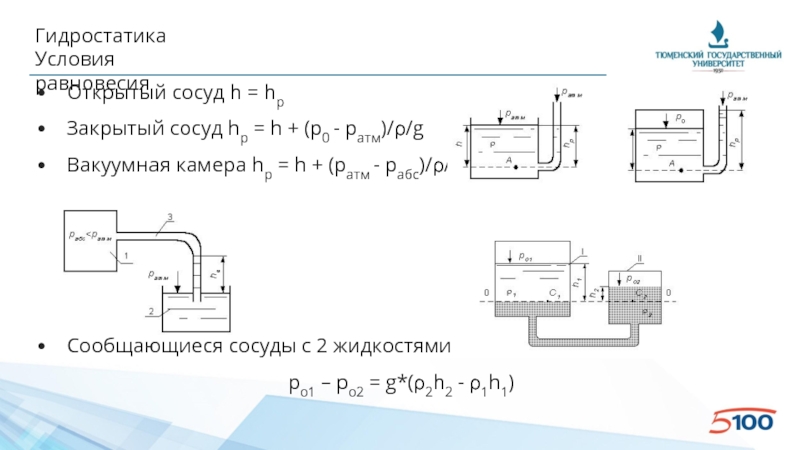
• Открытый сосуд h = hp
• Закрытый сосуд hp = h +
• Вакуумная камера hp = h + (pатм - pабс)/ρ/g
• Сообщающиеся сосуды с 2 жидкостями
po1 – po2 = g*(ρ2h2 - ρ1h1)
Слайд 75Гидростатика
Сообщающиеся сосуды с 2 жидкостями
• В сосудах налита одинаковая жидкость, но давления
po1 – po2 = g*ρ*(h2 - h1)
• В сосудах налита одинаковая жидкость и давления одинаковы (принцип сообщающихся сосудов)
h1 = h2
• Жидкость одинакова, но один сосуд открыт, а другой закрыт
hp = h + (pатм - pабс)/ρ/g
• Жидкости разнородные, несмешивающиеся, а давления сопадают
ρ2h2 = ρ1h1
Слайд 76Гидростатика
Пример 1
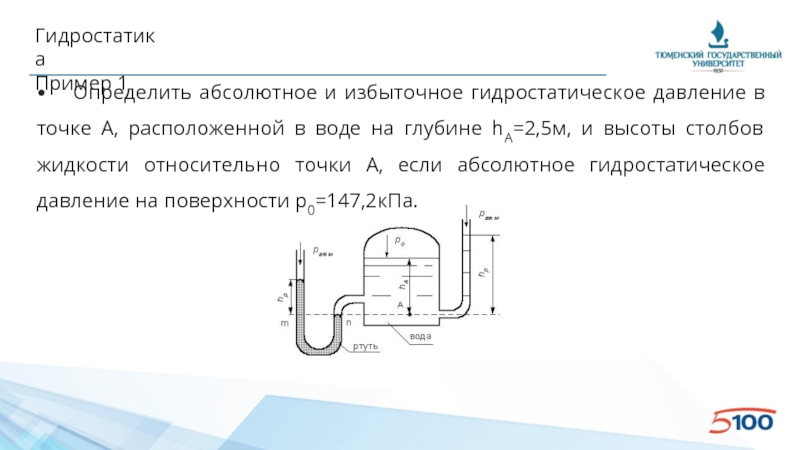
• Определить абсолютное и избыточное гидростатическое давление в точке А,
Слайд 77Гидростатика
Пример 1
• Согласно основному уравнению гидростатики:
pабс = p0 + ρ*g*h =
• Избыточное давление:
pизб = pабс - pатм = 70,375кПа
• Высота столба жидкости равна (ρрт = 13,6*103кг/м3):
hp = pизб/ρ/g
Слайд 78Гидростатика
Пример 2
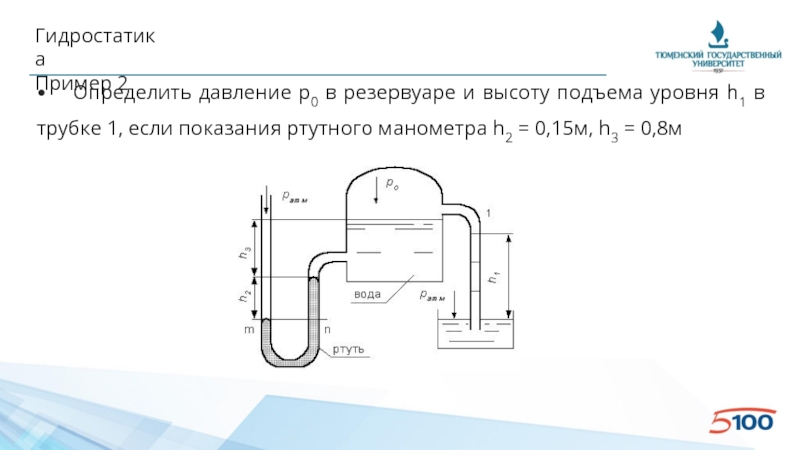
• Определить давление p0 в резервуаре и высоту подъема уровня
Слайд 79Гидростатика
Пример 2
• Условие равновесия для ртутного манометра для плоскости:
pатм = p0
p0 = pатм - ρв*g*h3 - ρрт*g*h2
• Условие равновесия трубки 1:
p0 + ρв*g*h1 = pатм
Слайд 80Гидростатика
Задача 1
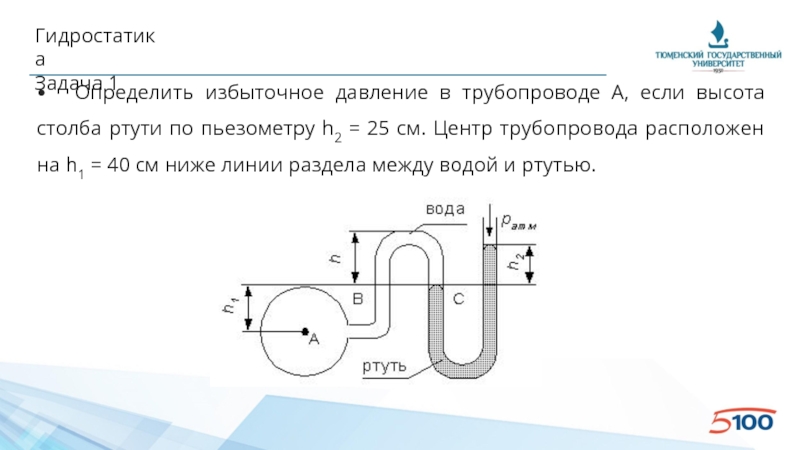
• Определить избыточное давление в трубопроводе А, если высота столба
Слайд 81Гидростатика
Задача 2
• Определить избыточное давление воды в трубе по показаниям батарейного
Слайд 82Гидростатика
Закон Паскаля
• Давление, производимое на жидкость или газ, передается в любую
Слайд 83Гидростатика
Давление на стенки сосуда
• Объединяем закон Паскаля и основное уравнение гидростатики:
p =
Слайд 84Гидростатика
Закон Архимеда
• На тело, погружённое в жидкость (или газ), действует выталкивающая
FA = ρ*g*V
• Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела
pB – pA = ρ*g*h
FB – FA = ρ*g*h*S
Слайд 85Гидростатика
Условия плавания тел
• FA < FT — тело тонет
• FA =
• FA > FT — тело всплывает до тех пор, пока не начнёт плавать
• ρA < ρT — тело тонет
• ρA = ρT — тело плавает в жидкости или газе
• ρA > ρT — тело всплывает до тех пор, пока не начнёт плавать
Слайд 86Гидростатика
Равновесие плавающего тела
• Для однородного тела плавающего на поверхности справедливо соотношение
Vпогр/V
Слайд 87Гидростатика
Примеры расчётов
• Определить, будет ли плавать на поверхности воды прямоугольная баржа,
• Вес тела в воде в 2,7 раза меньше, чем в воздухе. Какая плотность вещества, из которого изготовлено тело?
Слайд 88Гидростатика
Примеры расчётов
• Полый железный шар взвешивают в воздухе и керосине. Показания
• Лёд плавает в сосуде. Лёд растаял. Как изменится уровень воды?
• Пластиковая коробка с железками плавает в сосуде. Железки выпали за борт. Тот же вопрос.
• Лёд с замороженными железками (с полостью) внутри плавает в сосуде. Лед растаял. Тот же вопрос.
Слайд 91Течение жидкости в трубопроводе
• Режимы течения жидкости в трубопроводе
• Законы сохранения энергия, массы
• Кинематика жидкости
• Динамика жидкости
• Уравнение Эйлера
• Уравнение Бернулли
• Уравнение Навье-Стокса
• Уравнение Эйлера
Слайд 92Течение жидкости в трубопроводе
Режимы течения жидкости в трубопроводе
• Режимы течения жидкости и
ламинарные (струйные) - при невысокой скорости течения слои (потоки частиц) почти не перемешиваются и движутся по параллельным траекториям
турбулентные - после преодоления некоего критического значения (для различных условий оно разное), названного числом Рейнольдса, режимы течения жидкости меняются: струйный поток становится хаотичным, вихревым. Важное свойство турбулентности: оно всегда трехмерно.
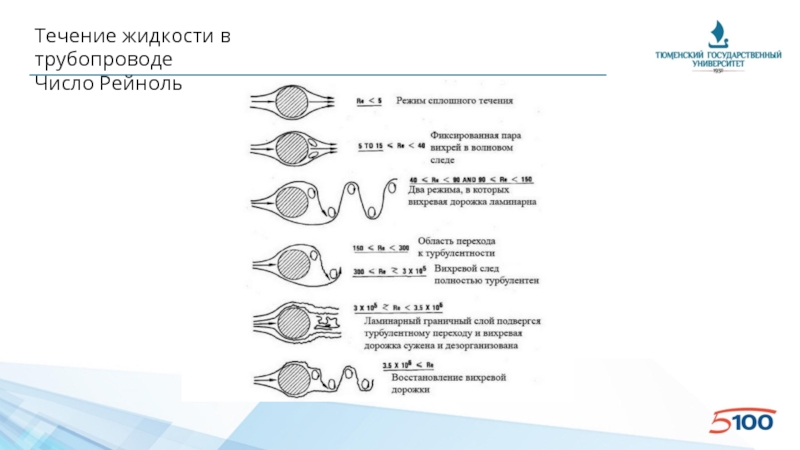
Слайд 93Течение жидкости в трубопроводе
Число Рейнольдса
• В трубах, имеющих круглое сечение (такие используют
Recr = (ρudэ/µ)cr
ρ – плотность потока, u – характерная скорость потока; L – характерный размер потока (эквивалентный диаметр), µ – коэффициент динамической вязкости, cr – течение по трубе с круглым сечением, П – смоченный периметр
Слайд 95Течение жидкости в трубопроводе
Примеры
• По трубопроводу диаметром 270×10 мм перекачивается вода с
• Бензол с расходом 200 т/час и средней температуре 40ºС поступает в трубный пучок одноходового кожухотрубчатого теплообменника, состоящего из 717 труб диаметром d×δ = 20×2 мм. Определить скорость бензола в трубах трубного пучка и режим его движения в них.
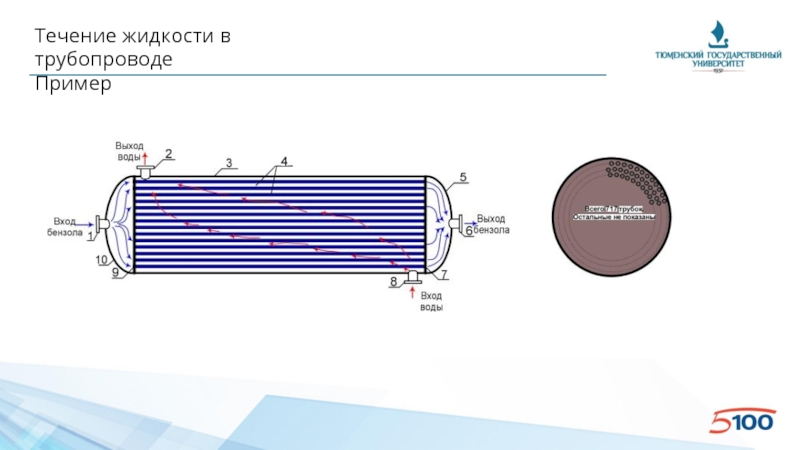
Слайд 97Течение жидкости в трубопроводе
Примеры
• Для охлаждения бензола в межтрубное пространство кожухотрубчатого
Слайд 98Течение жидкости в трубопроводе
Уравнение непрерывности
∇ — дивергенция,
ρ — количество величины q на единицу объёма (плотность
t — время,
j — плотность потока величины q,
σ — добавление q на единицу объёма в единицу времени. Члены, которые добавляют (σ > 0) или удаляют (σ < 0) q, называются «источниками» и «стоками» соответственно.
Слайд 99Течение жидкости в трубопроводе
Уравнение сохранения
• Если q — сохраняющаяся величина
• Уравнение сохранения массы
j = ρv –
Слайд 100Течение жидкости в трубопроводе
Примеры
• На трубопроводе имеется переход с диаметра 50
объёмный и массовый расходы воды;
скорость воды в широком сечении;
режимы течения в узком и широком сечениях.
Слайд 101Течение жидкости в трубопроводе
Примеры
• Азот с расходом 6400 м3/час (при н.у.)
скорость азота на входе в трубный пучок и на выходе из него;
режим движения азота на входе и на выходе.
Слайд 102Течение жидкости в трубопроводе
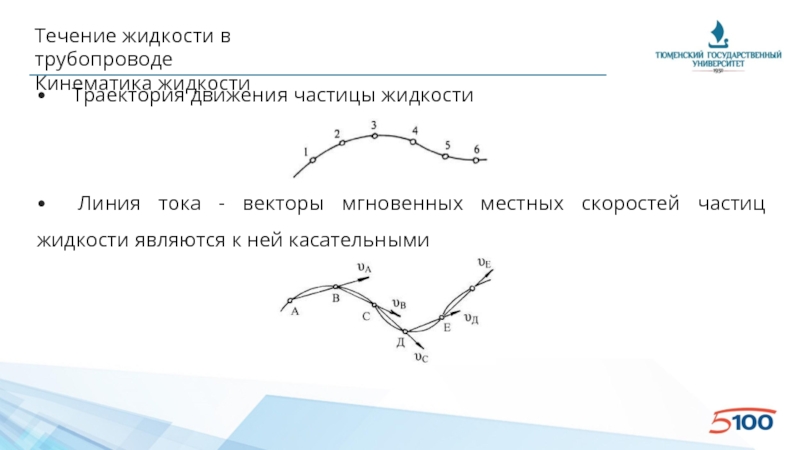
Кинематика жидкости
• Траектория движения частицы жидкости
• Линия тока
Слайд 103Течение жидкости в трубопроводе
Характер движения жидкости
• Установившееся (стационарное) движение – это
• Неустановившемся движением называют течение жидкости, когда в точках области, где движется жидкость, местные скорости изменяются с течением времени и его описывают уравнением u = ƒ(х, у, z, t). При неустановившемся движении линии тока и траектории частиц не совпадают.
Слайд 104Течение жидкости в трубопроводе
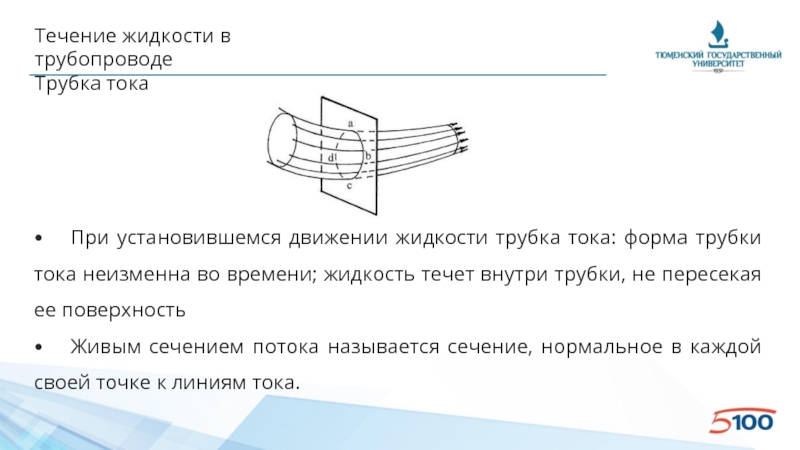
Трубка тока
• При установившемся движении жидкости трубка тока:
• Живым сечением потока называется сечение, нормальное в каждой своей точке к линиям тока.
Слайд 105Течение жидкости в трубопроводе
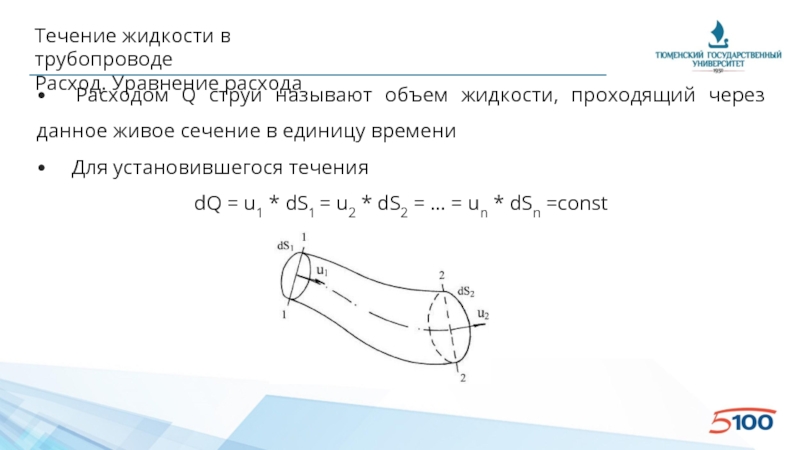
Расход. Уравнение расхода
• Расходом Q струи называют объем
• Для установившегося течения
dQ = u1 * dS1 = u2 * dS2 = … = un * dSn =const
Слайд 106Течение жидкости в трубопроводе
Потоки жидкости
• Потоком жидкости называют движущуюся массу жидкости, ограниченную
безнапорные потоки ограничены частично твердой, частично свободной поверхностью
напорные потоки ограничены твердыми поверхностями по всему сечению, и гидродинамическое давление в любой точке потока отлично от атмосферного
гидравлические струи ограничены только жидкостью или газовой средой.
Слайд 107Течение жидкости в трубопроводе
Гидравлические элементы потока
• Смоченный периметр χ представляет собой длину
• Гидравлический радиус R - отношение площади живого сечения потока к смоченному периметру в этом сечении
R = S/χ
Слайд 108Течение жидкости в трубопроводе
Динамика жидкости
• Уравнение Бернулли
• Измерение расходов и скоростей жидкости
• Примеры расчётов
Слайд 109Течение жидкости в трубопроводе
Уравнение Бернулли
• Уравнение Бернулли для элементарной струйки идеальной несжимаемой
z1 + p1/ρ/g + (u1)2/2/g = z2 + p2/ρ/g + (u2)2/2/g
• Полный напор в данном сечении струйки = геометрический + пъезометрический напор + скоростной напор = const
Слайд 110Течение жидкости в трубопроводе
Энергетическая интерпретация уравнения Бернулли
z1 + p1/ρ/g + (u1)2/2/g
• Полная удельная энергия = удельная потенциальная энергия + удельная энергия давления (сжатия) + удельная кинетическая энергия = const
• Удельная потенциальная энергия + удельная энергия давления (сжатия) = удельная потенциальная энергия
Слайд 111Течение жидкости в трубопроводе
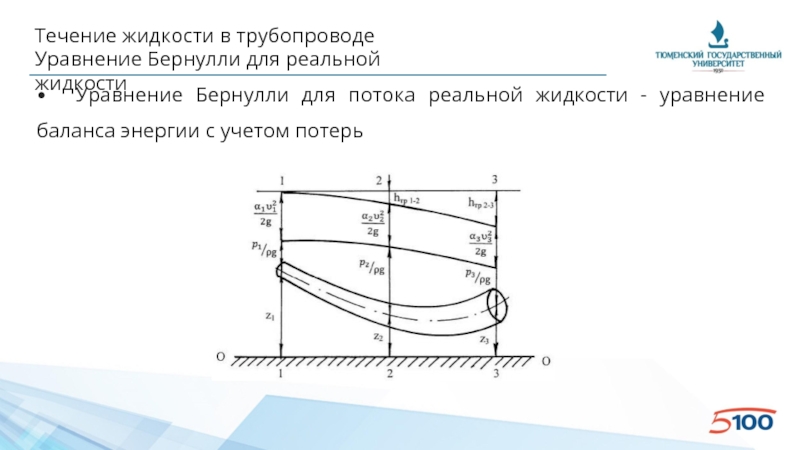
Уравнение Бернулли для реальной жидкости
• Уравнение Бернулли для элементарной
z1 + p1/ρ/g + α1(u1)2/2/g = z2 + p2/ρ/g + α2(u2)2/2/g + hтр
• α1 и α1 – коэффициенты Кариолиса в двух сечениях, hтр – потери удельной энергии (напора) на участке между сечениями
Слайд 112Течение жидкости в трубопроводе
Уравнение Бернулли для реальной жидкости
• Уравнение Бернулли для
Слайд 113Течение жидкости в трубопроводе
Уравнение Бернулли. Напорная линия
• Гидравлический уклон J - отношение
J = hтр/ℓ
• Коэффициент α - коэффициент кинетической энергии или коэффициент Кариолиса. Коэффициент учитывает неравномерность распределения скоростей частиц жидкости в сечении реального потока (в пределах от 1 до 2)
Eк = α1(u1)2/2/g
Слайд 114Течение жидкости в трубопроводе
Измерение расходов и скоростей жидкости
• Объемный способ измерения
Q = V*t
• Весовой способ измерения - находят вес всей жидкости, поступившей в сосуд за время t, и зная плотность жидкости, определяют весовой расход как
Q = G/(ρgt)
Слайд 115Течение жидкости в трубопроводе
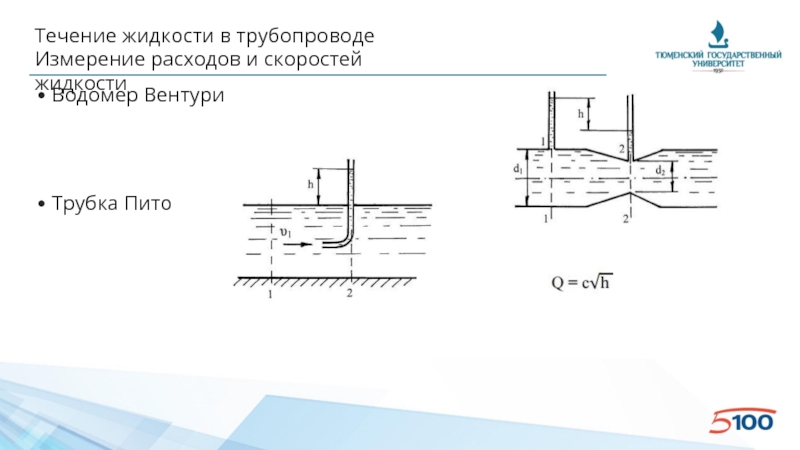
Измерение расходов и скоростей жидкости
• Водомер Вентури
• Трубка
Слайд 116Течение жидкости в трубопроводе
Уравнение Бернулли. Пример
• Из напорного бака вода течет
Слайд 117Течение жидкости в трубопроводе
Уравнение Бернулли. Пример. Решение
Ввиду значительных размеров сосуда по
Слайд 118Течение жидкости в трубопроводе
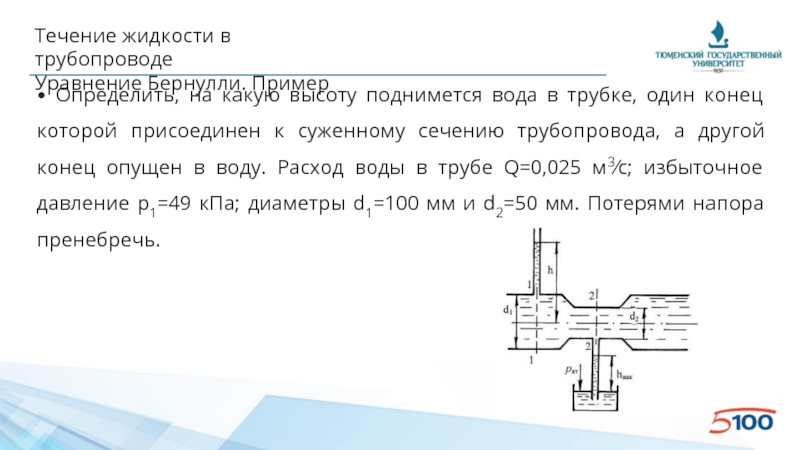
Уравнение Бернулли. Пример
• Определить, на какую высоту поднимется
Слайд 120Течение жидкости в трубопроводе
Методы Эйлера и Лагранжа
• Метод Эйлера основывается на анализе течения жидкости в
• Метод Лагранжа основывается на анализе течения каждой частицы жидкости, то есть траектории их течения.
Слайд 121Течение жидкости в трубопроводе
Уравнения Эйлера для движущейся идеальной жидкости
• X, Y, Z
Слайд 122Течение жидкости в трубопроводе
Уравнения Эйлера для движущейся идеальной жидкости
• Уравнения не учитывают
• Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается системой уравнений Эйлера.
Слайд 123Течение жидкости в трубопроводе
Метод Лагранжа
• Рассматривается движение каждой частицы жидкости
• В начальный момент
При движении частицы ее координаты зависят от времени
x = x(x0, y0, z0, t); y = y(x0, y0, z0, t); z = z(x0, y0, z0, t)
Здесь x0, y0, z0, t – параметры Лагранжа.
Слайд 124Течение жидкости в трубопроводе
Уравнения Навье-Стокса
• В векторном виде для несжимаемой жидкости
• При учёте
ν — коэффициент кинематической вязкости, f — векторное поле массовых сил, η — коэффициент динамической вязкости (сдвиговая вязкость), ζ — «вторая вязкость», или объёмная вязкость.
Слайд 125Течение жидкости в трубопроводе
Уравнения Навье-Стокса
• Система дифференциальных уравнений в частных производных, описывающая
Слайд 126Течение жидкости в трубопроводе
Уравнения Навье-Стокса. Основные свойства
• При превышении числа Рейнольдса некоторой критической величины
• Исключительная чувствительность к изменению коэффициентов уравнения при турбулентном режиме: при изменении числа Re на 0,05 % решения совершенно отличаются друг от друга.
Слайд 128Неньютоновские жидкости
• Неньютоновская жидкость - жидкость, при течении которой её вязкость зависит от градиента скорости.
• Для неньютоновских жидкостей невозможно использовать уравнения Навье-Стокса
• 1 – ньютоновская, 2 – псевдопластичная, 3 – дилатантная,
4 – вязкопластичная (τ - касательное напряжение)
Слайд 132Структура многофазного потока
• Многофазные потоки возникают при протекании газа через жидкость (пробулькивание,
• Режимы многофазного потока: пузырьковая, пробковый (совокупность больших и малых, плоских пузырей различной формы, разделенных жидкостными перемычками), снарядно-пробковая, пробково-кольцевая, кольцевая, дисперсно-кольцевая, дисперсная
Слайд 133Структура многофазного потока
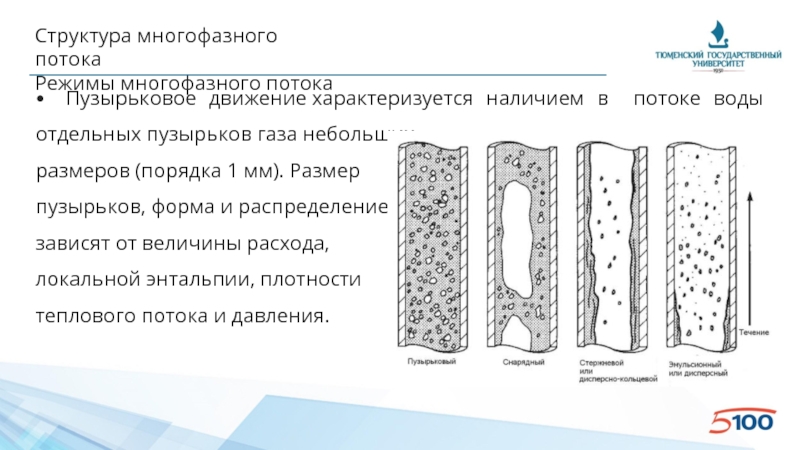
Режимы многофазного потока
• Пузырьковое движение характеризуется наличием в потоке воды отдельных
размеров (порядка 1 мм). Размер
пузырьков, форма и распределение
зависят от величины расхода,
локальной энтальпии, плотности
теплового потока и давления.
Слайд 134Структура многофазного потока
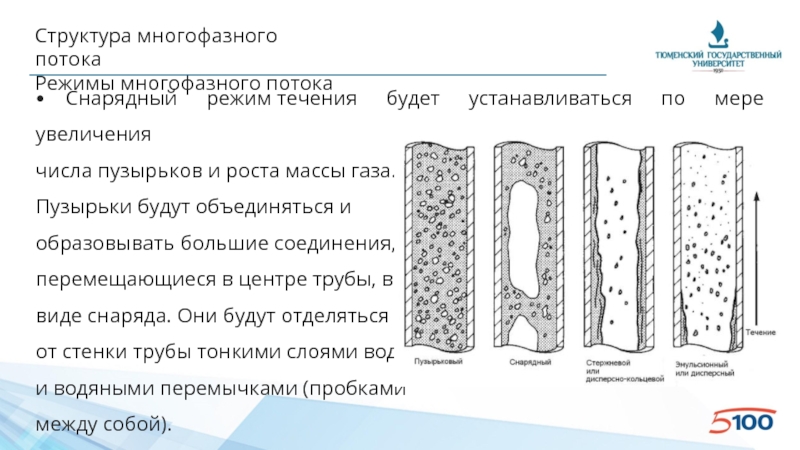
Режимы многофазного потока
• Снарядный режим течения будет устанавливаться по мере увеличения
числа
Пузырьки будут объединяться и
образовывать большие соединения,
перемещающиеся в центре трубы, в
виде снаряда. Они будут отделяться
от стенки трубы тонкими слоями воды
и водяными перемычками (пробками
между собой).
Слайд 135Структура многофазного потока
Режимы многофазного потока
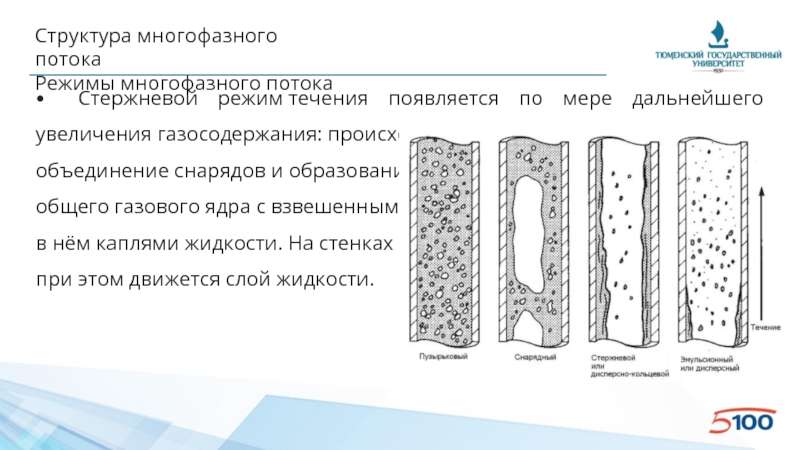
• Стержневой режим течения появляется по мере дальнейшего
объединение снарядов и образование
общего газового ядра с взвешенными
в нём каплями жидкости. На стенках
при этом движется слой жидкости.
Слайд 136Структура многофазного потока
Режимы многофазного потока
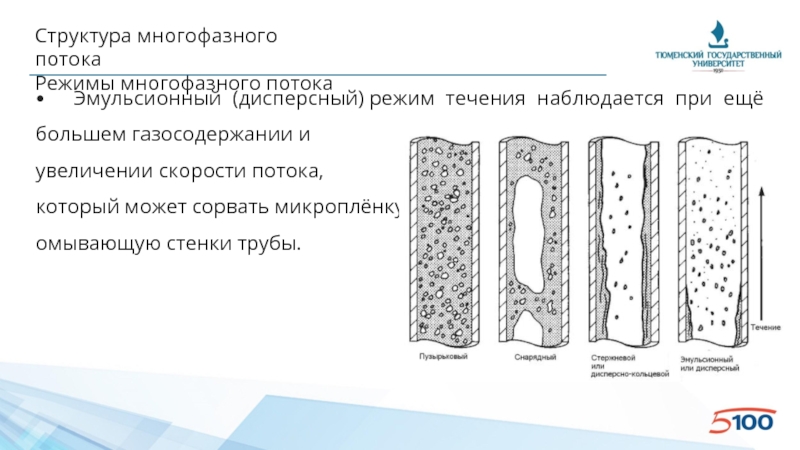
• Эмульсионный (дисперсный) режим течения наблюдается при ещё
увеличении скорости потока,
который может сорвать микроплёнку,
омывающую стенки трубы.
Слайд 137Структура многофазного потока
Карта Тайтеля-Даклера
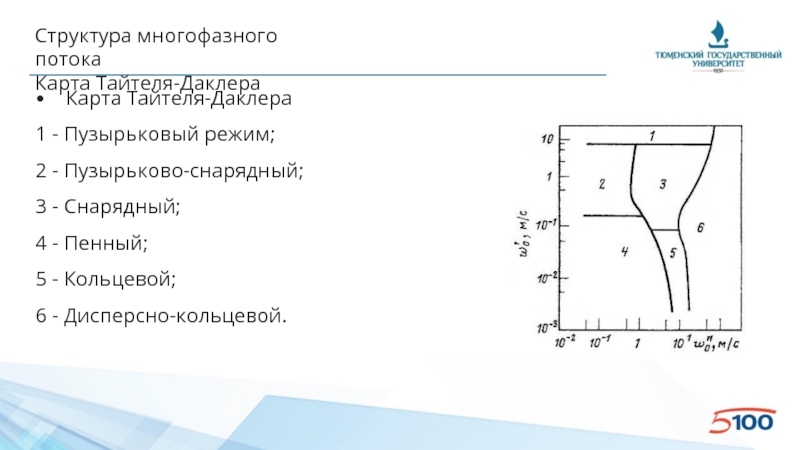
• Карта Тайтеля-Даклера
1 - Пузырьковый режим;
2 - Пузырьково-снарядный;
3 -
4 - Пенный;
5 - Кольцевой;
6 - Дисперсно-кольцевой.