- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Физика колебаний и волн презентация
Содержание
- 1. Физика колебаний и волн
- 2. Общие представления о колебательных и волновых процессах.
- 3. Общие представления о колебательных и волновых процессах.
- 4. Общие представления о колебательных и волновых процессах.
- 5. Гармонические колебания и их характеристики Наиболее простой
- 6. Гармонические колебания и их характеристики или
- 7. Гармонические колебания и их характеристики Связь между
- 8. Гармонические колебания
- 9. Гармонические колебания В итоге получим:
- 10. Гармонические колебания
- 11. Гармонические колебания Произведем преобразования по аналогии с
- 12. Гармонические колебания Колебания кинетической энергии
- 13. Гармонический осциллятор Любую колебательную систему называют
- 14. Общая физика. Физика колебаний и волн Гармонический осциллятор Математический маятник.
- 15. Общая физика. Физика колебаний и волн Гармонический
- 16. Общая физика. Физика колебаний и волн Гармонический
- 17. Общая физика. Физика колебаний и волн Гармонический осциллятор Математический маятник.
- 18. Общая физика. Физика колебаний и волн Гармонический
- 19. Общая физика. Физика колебаний и волн Гармонический
- 20. Общая физика. Физика колебаний и волн
- 21. Общая физика. Физика колебаний и волн Гармонический
- 22. Общая физика. Физика колебаний и волн Гармонический осциллятор Пружинный маятник.
- 23. Общая физика. Физика колебаний и волн Гармонический
Слайд 1
ЛЕКЦИЯ 7
ПЛАН ЛЕКЦИИ
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Общие представления о колебательных и волновых
Гармонические колебания и их характеристики.
Гармонический осциллятор.
Примеры гармонических осцилляторов. Математический маятник
Слайд 2Общие представления о колебательных и волновых процессах.
Колебания - это процессы, повторяющиеся
Колебательные процессы наблюдаются в системах различной физической природы. Примеры: колебания груза на пружине, колебания маятника, колебания тока в электрическом контуре и т. д.
В системах с бесконечным числом степеней свободы (сплошная среда) колебательный процесс распространяется в пространстве. В пространстве распространяется волна. Волна характеризуется периодичностью как во времени, так и в пространстве. Примеры: звуковые волны, электромагнитные волны и т.д.
Слайд 3Общие представления о колебательных и волновых процессах.
Использование колебательных процессов:
- часы
радиоприемники и телевизоры (колебательные контуры);
связь (электромагнитные волны);
другое.
Типы колебаний: свободные и вынужденные, автоколебания и параметрические колебания.
Свободные (собственные) - колебания, которые развиваются в системе, представленной самой себе после того, как она была выведена из состояния равновесия. Совершаются за счет первоначально сообщенной энергии. Пример: колебания груза на пружине в поле сил тяготения.
Слайд 4Общие представления о колебательных и волновых процессах.
Вынужденные - колебания, в процессе
Автоколебания поддерживаются за счет внешнего источника энергии. Но: автоколебательная система сама управляет внешними воздействиями, обеспечивая поступление энергии в такт с колебаниями. Пример – механические часы. Храповой механизм часов подталкивает маятник в такт с его колебаниями. Внешний источник энергии - сжатая пружина либо опускающийся груз.
Параметрические колебания. Внешнее воздействие периодически изменяет какой либо параметр системы, определяющий ее свойства. Пример: в процессе колебаний маятника может периодически изменяться длина нити, на которой подвешен маятник.
Слайд 5Гармонические колебания и их характеристики
Наиболее простой вид колебаний. Изучение гармонических колебаний
Гармонические колебания - колеблющаяся величина изменяется со временем по закону косинуса (синуса).
а) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
б) различные периодические процессы можно представить как наложение периодических колебаний.
Колебания различной природы подчиняются одинаковым законам. Пример: колебания груза, подвешенного на пружине, и изменение заряда конденсатора в колебательном контуре происходят по одному и тому же закону.
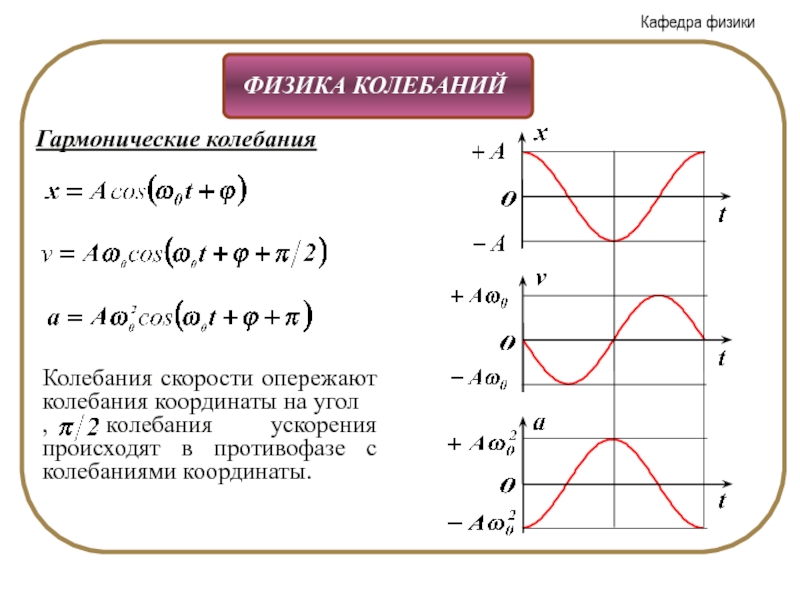
Слайд 7Гармонические колебания и их характеристики
Связь между параметрами гармонических колебаний:
Скорость и
Скорость и ускорение колеблющейся точки изменяются со временем по гармоническому закону.
Слайд 11Гармонические колебания
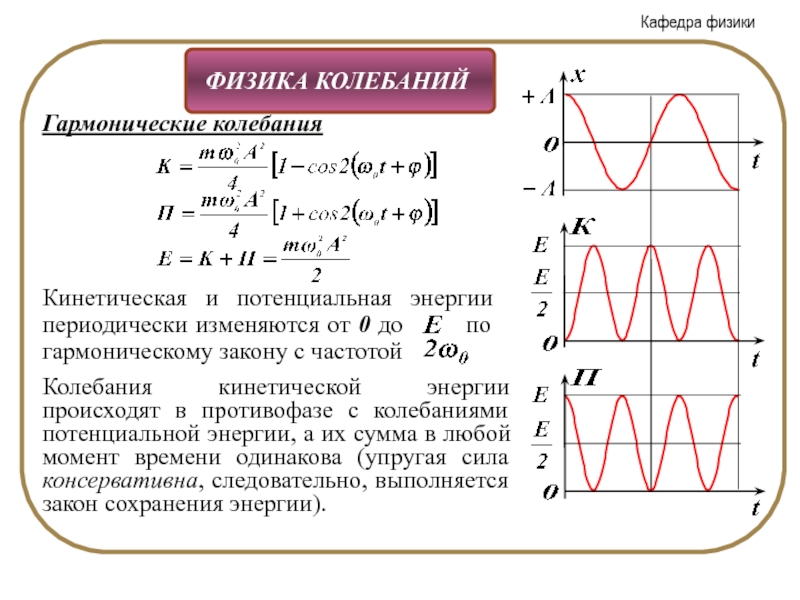
Произведем преобразования по аналогии с выводом формулы для К. Воспользуемся
В итоге получим:
Полная энергия:
Слайд 12Гармонические колебания
Колебания кинетической энергии происходят в противофазе с колебаниями потенциальной энергии,
Слайд 13Гармонический осциллятор
Любую колебательную систему называют осциллятором. Если поведение осциллятора подчиняется
Определим вид уравнения гармонического осциллятора. Для этого используем вторую производную от уравнения движения колеблющейся материальной точки:
Это дифференциальное уравнение гармонических колебаний.
Решение этого уравнения:
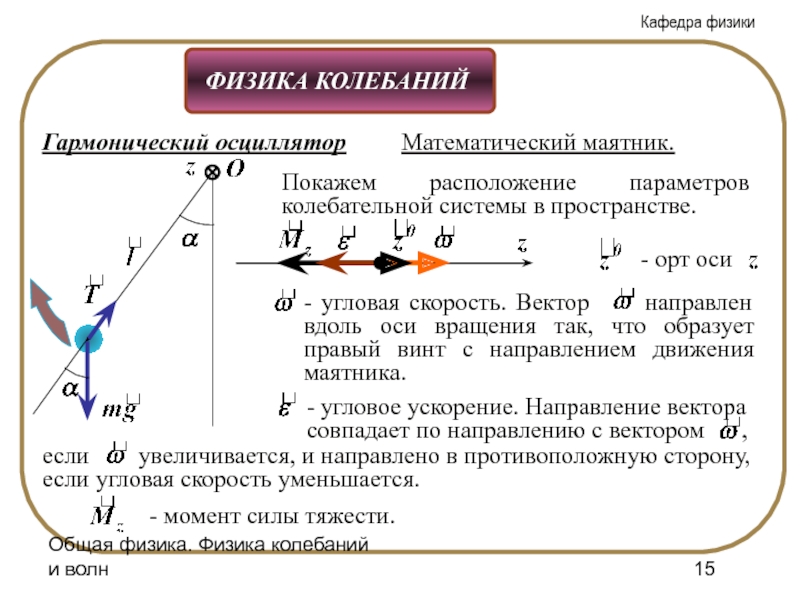
Слайд 15Общая физика. Физика колебаний и волн
Гармонический осциллятор
Математический маятник.
Покажем расположение параметров
Слайд 16Общая физика. Физика колебаний и волн
Гармонический осциллятор
Математический маятник.
Пренебрежем силами трения
Слайд 18Общая физика. Физика колебаний и волн
Гармонический осциллятор
Математический маятник.
Знак «минус» означает,
Окончательно получим:
Это нелинейное дифференциальное уравнение, описывающее движение математического маятника при любой величине угла отклонения от вертикали.
Слайд 19Общая физика. Физика колебаний и волн
Гармонический осциллятор
Математический маятник.
Период этих колебаний
Решение полученного уравнения:
Слайд 20Общая физика. Физика колебаний и волн
Гармонический осциллятор
Физический маятник.
Физический маятник –
Вывод уравнения движения физического маятника идентичен выводу уравнения движения математического маятника.
Слайд 21Общая физика. Физика колебаний и волн
Гармонический осциллятор
Физический маятник.
Отличие - в
Получим такие же уравнения, как и для математического маятника:
Пусть собственная частота колебаний физического маятника выражается как
решение:
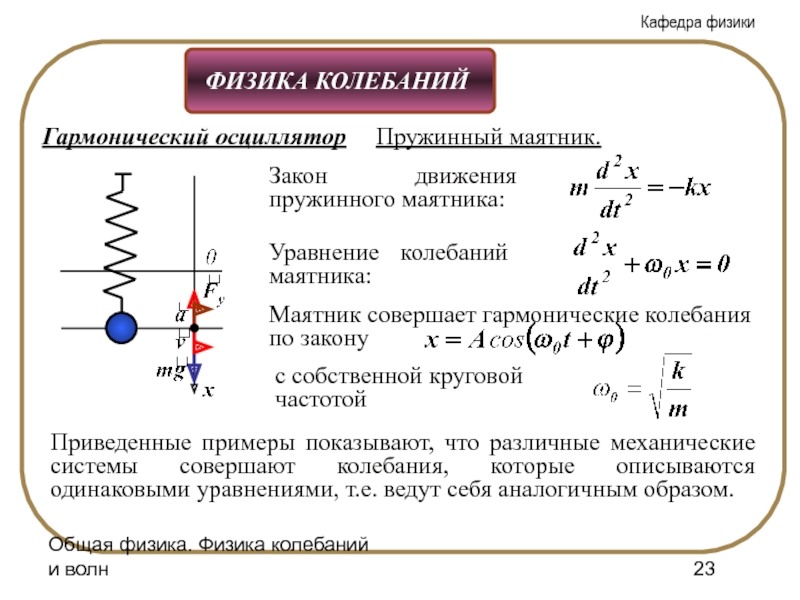
Слайд 23Общая физика. Физика колебаний и волн
Гармонический осциллятор
Пружинный маятник.
Закон движения пружинного
Уравнение колебаний маятника:
с собственной круговой частотой
Приведенные примеры показывают, что различные механические системы совершают колебания, которые описываются одинаковыми уравнениями, т.е. ведут себя аналогичным образом.