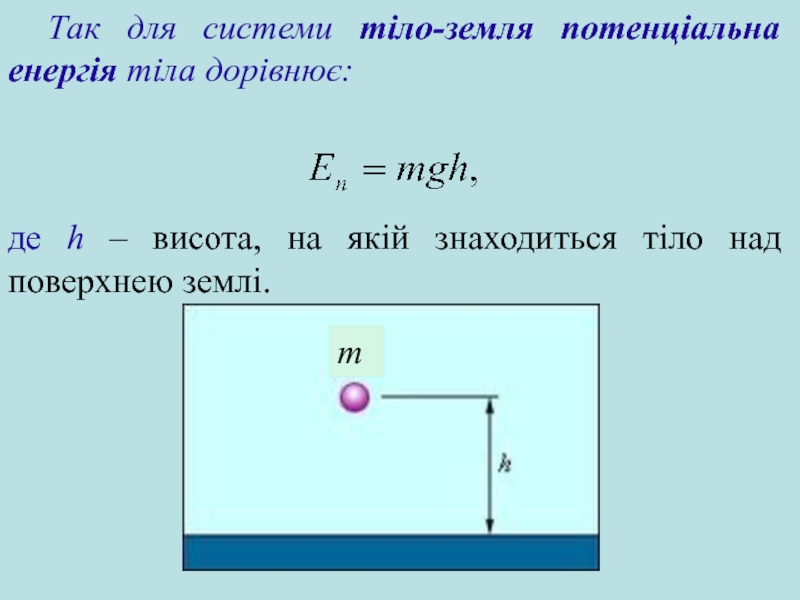
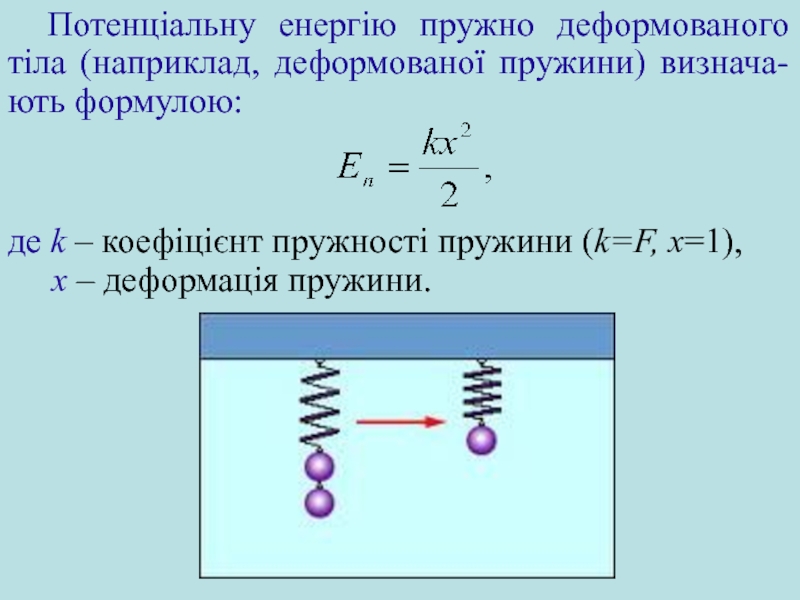
Потенціальна енергія. Енергія пружно деформованого тіла
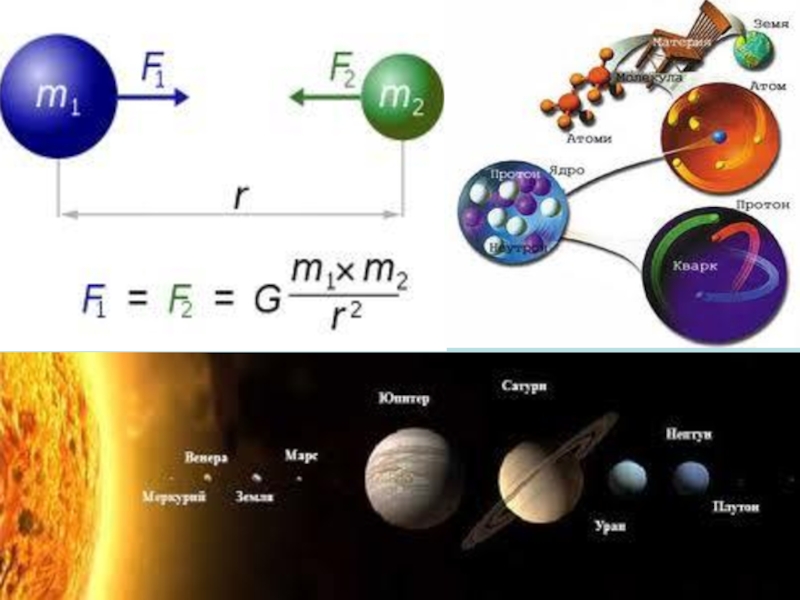
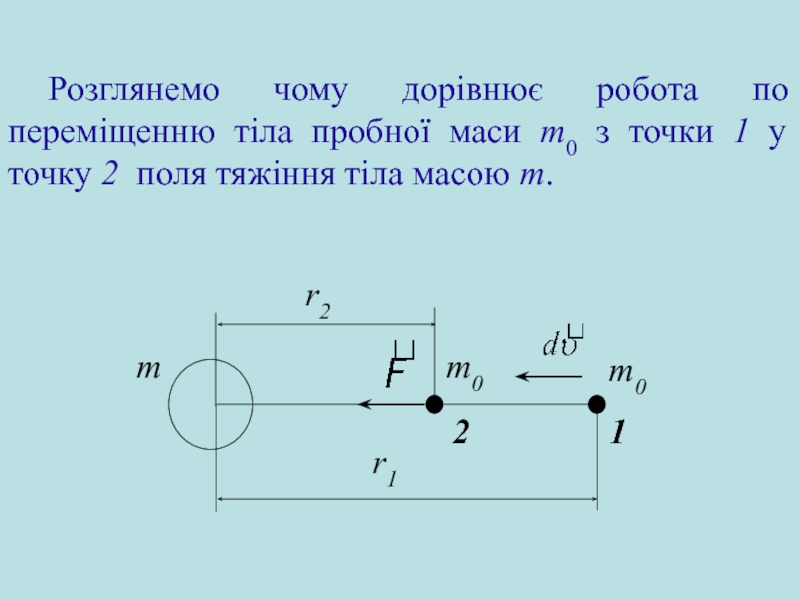
Гравітаційне поле та його характеристики. Потенціальна енергія матеріальної точки у гравітаційному полі
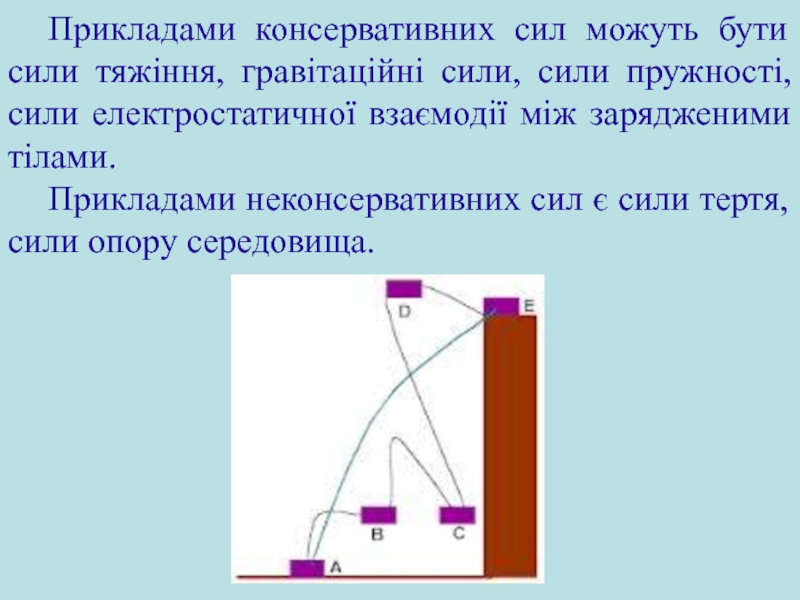
Потенціальні сили та консервативні системи
Закон збереження енергії у механіці
Лекція № 5.
Енергія, робота та потужність
Закон збереження енергії