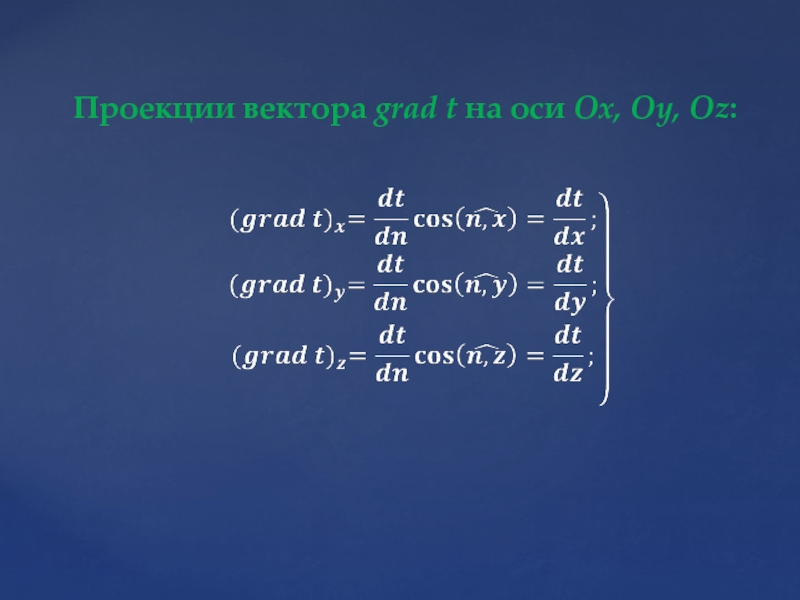- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные положения учения о теплопроводности презентация
Содержание
- 1. Основные положения учения о теплопроводности
- 2. Теплопередача или теплообмен — учение о самопроизвольных необратимых процессах распространения теплоты в пространстве.
- 3. Методы изучения физических явлений феноменологический статистический Плюсы
- 4. Температурное поле Теплопроводность обусловлена движением микрочастиц вещества. Математическое выражение температурного поля:
- 5. Уравнение для одномерного поля: Простой вид уравнения одномерного стационарного температурного поля:
- 6. Температурный градиент Изотермической поверхностью называется геометрическое место
- 7. Проекции вектора grad t на оси Ox, Oy, Oz:
- 8. Тепловой поток. Закон Фурье. Для передачи
- 9. Изотермы и линии теплового тока dF-элемент изотермической поверхности.
- 10. Проекции на плоскости:
- 11. Коэффициент теплопроводности Порядок значений коэффициентов теплопроводности различных веществ Коэффициент теплопроводности, Вт/(м*К):
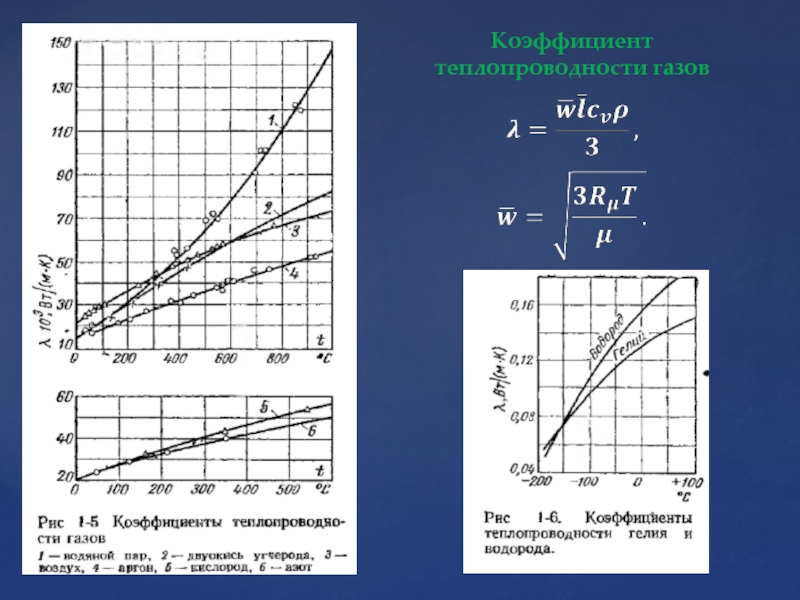
- 12. Коэффициент теплопроводности газов
- 13. Коэффициент теплопроводности жидкости Коэффициент теплопроводности капельных
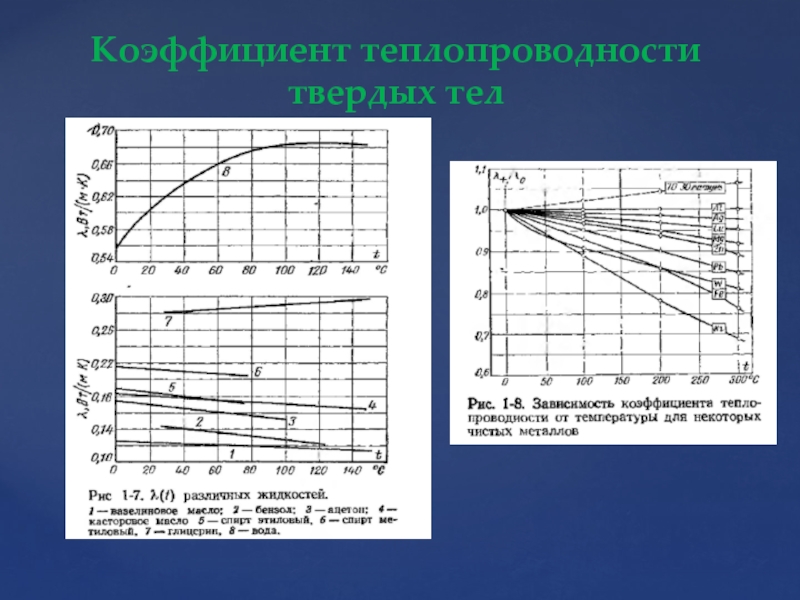
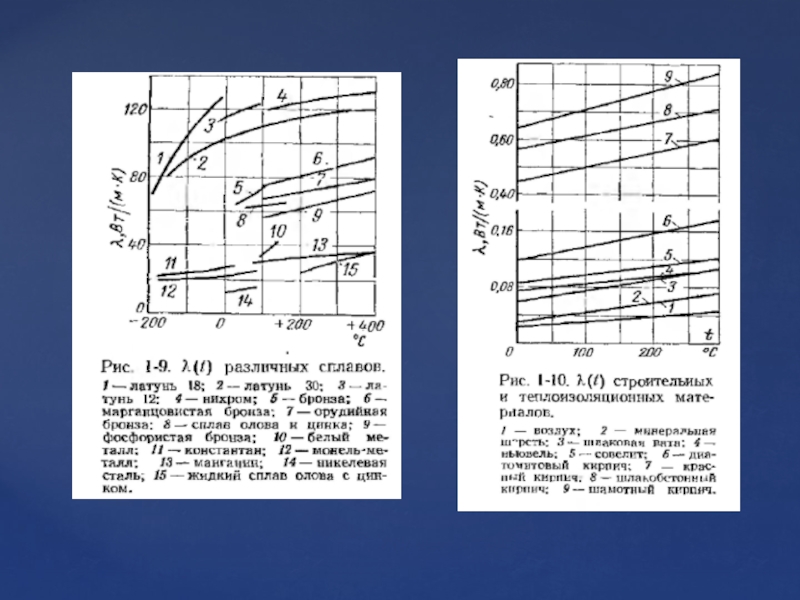
- 14. Коэффициент теплопроводности твердых тел
- 16. Дифференциальное уравнение теплопроводности
- 17. Если ограничиться двумя первыми членами ряда, то:
- 18. Если система тел не содержит внутренних источников
- 19. Лекция №2 «Теплопроводность при стационарном режиме»
- 20. Передача теплоты через плоскую стенку ( qv=0 ) или если qv=0, то:
- 21. Граничные условия первого рода. Если ось
- 22. После второго интегрирования: Постоянные С1 и С2 определяются из:
- 23. Закон распределения температуры: - текущий температурный напор
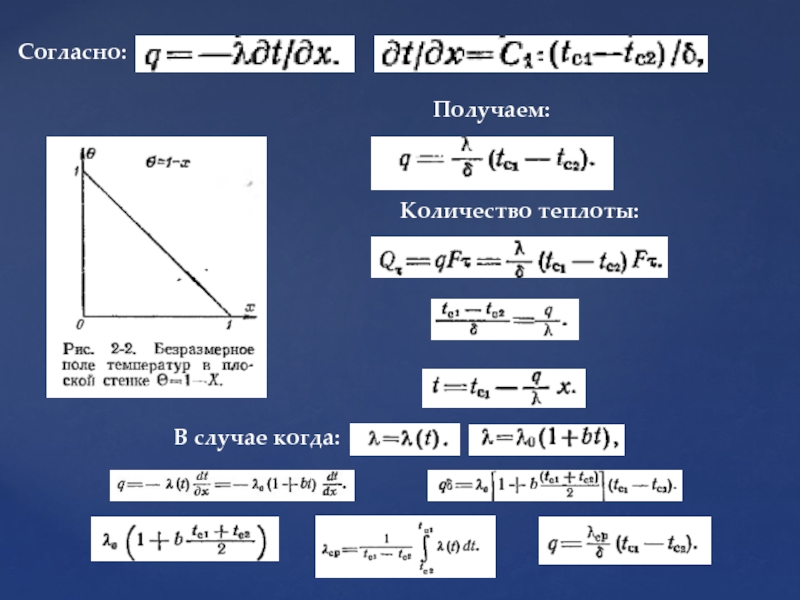
- 24. Согласно: Получаем: Количество теплоты: В случае когда:
- 27. Граничные условия третьего рода (теплопередача). Плотность
- 28. Сложив равенства получим: Отсюда плотность теплового потока: Обозначим: Тогда: Полное термическое сопротивление однослойной стенки :
- 29. Если стенка состоит из слоев, то полное
- 30. Температура при граничных условиях третьего рода:
- 31. Графический метод определения температур на поверхностях слоев
- 32. Граничные условия второго и третьего рода В
- 33. Передача теплоты через цилиндрическую стенку 1)
- 34. Введем новую переменную: Тогда: Интегрируем и получаем: Граничные условия:
- 35. Решение уравнения: или Согласно закону Фурье: Т. к. то
- 36. Тепловой поток, отнесенный к единице длины трубы,
- 37. 2) Граничные условия третьего рода (теплопередача) Температурный напор: Тогда:
- 38. Величина ki называется линейным коэффициентом теплопередачи, он
- 39. На практике часто встречаются цилиндры, толщина стенок
- 40. В случае теплопередачи через многослойную цилиндрическую стенку
- 41. В случае задания граничных условий первого рода
- 42. Пути интенсификации теплопередачи а) Интенсификация теплопередачи путем
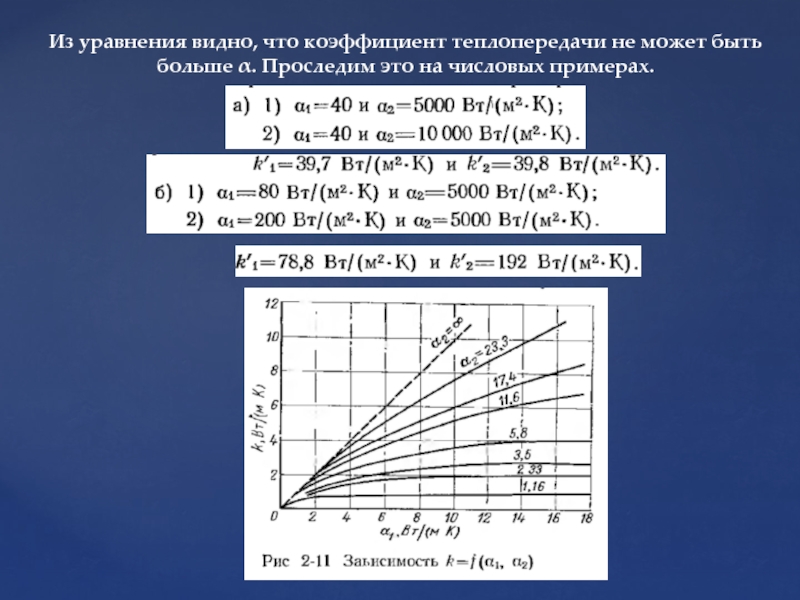
- 43. Из уравнения видно, что коэффициент теплопередачи не
- 44. б) Интенсификация теплопередачи за счет оребрения стенок
- 45. Теплопроводность круглого ребра постоянной толщины Рассмотрим расчет
- 46. Если температурой с торца круглого ребра пренебречь:
- 47. Лекция № 3 Основные положения учения о конвективном теплообмене.
- 48. Основные понятия и определения. Конвекция
- 49. Физические свойства жидкости. Процесс
- 50. Реальные жидкости обладают вязкостью; между частицами или
- 51. отношение вязкости μ к плотности р, называемое
- 52. На теплоотдачу оказывает влияние сжимаемость жидкостей.
- 53. Помимо изотермической сжимаемости для конвективного теплообмена большое
- 54. Дифференциальные уравнения конвективного теплообмена. Из уравнения:
- 55. Для реальной жидкости i=i(T, р), и согласно
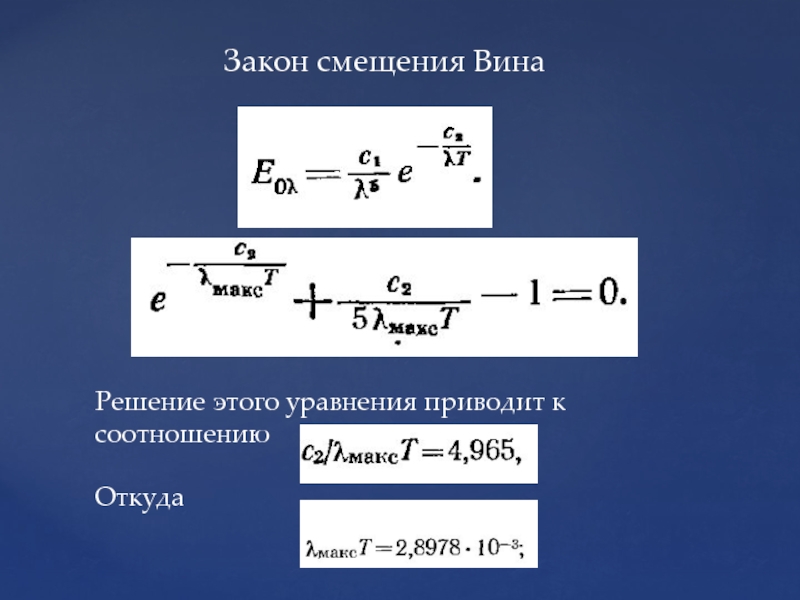
- 56. в предположении о несжимаемости жидкости. (р=const) с
- 57. Вывод уравнения энергии Где
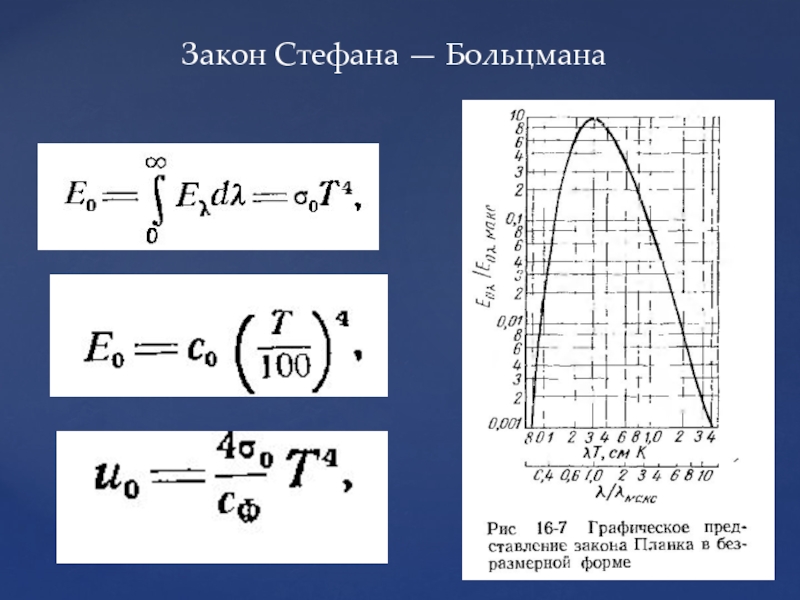
- 58. Подставляя значений qx, qy и qz в
- 59. Тогда
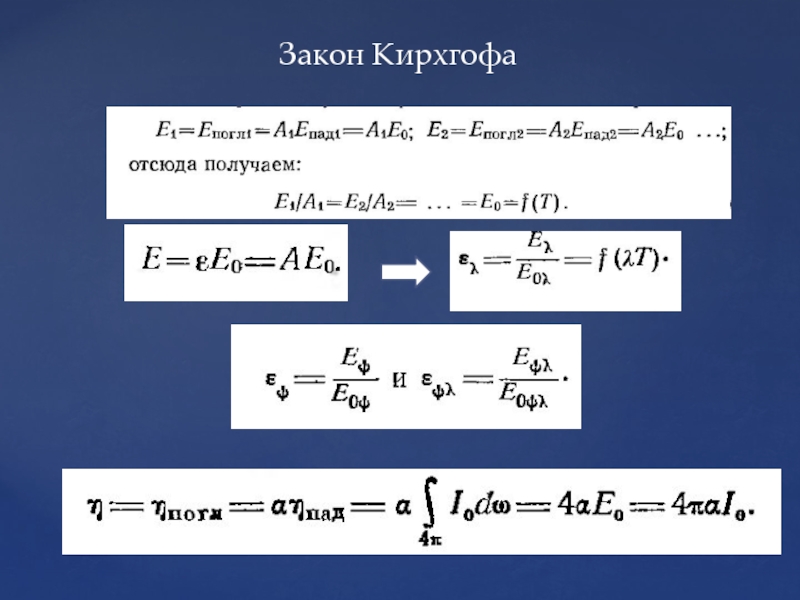
- 60. Здесь dt/dx характеризует изменение температуры во времени
- 61. При стационарных процессах конвективного теплообмена dt/dт=0.
- 62. Силы, действующие на рассматриваемый элемент жидкости, можно
- 63. Равнодействующая этих сил равна алгебраической сумме: Подставляя
- 64. Приравнивая правые части уравнений (а) и (б)
- 65. ДЛЯ оси ОY Для
- 66. Лекция № 4 Теплоотдача при вынужденном поперечном омывании труб и пучков труб.
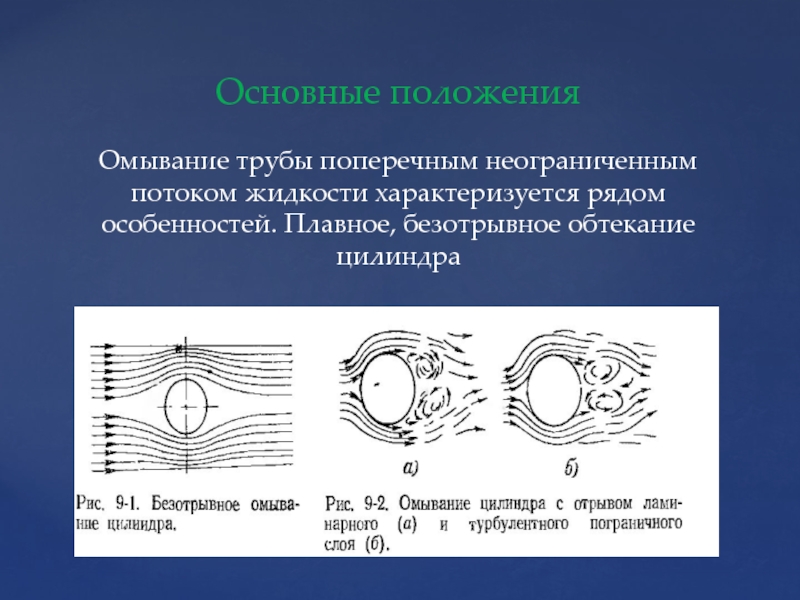
- 67. Основные положения Омывание трубы поперечным неограниченным
- 68. Теплоотдача при поперечном омывании пучков труб
- 69. Если учитывается только сила тяжести, то Свободное
- 70. Теплоотдача при свободном движении жидкости в большом
- 71. Будем полагать, что температура в движущемся слое жидкости изменяется по уравнению:
- 72. Для стационарного течения я с учетом ранее
- 73. Подставляя значение υ в уравнение и
- 74. Примем следующие граничные условия для скорости: wx=0
- 75. Среднеинтегральная скорость равна:
- 76. Подставляя значение
- 77. Можно считать, что в среднем жидкость нагревается
- 78. Постоянную интегрирования с найдем из условия, что
- 79. Приведем уравнение к безразмерному виду, для чего
- 80. Для расчета местных коэффициентов при свободном ламинарном
- 81. Теплоотдача при свободном турбулентном движении вдоль вертикальной
- 82. Теплоотдача при переходном режиме свободного движения вдоль
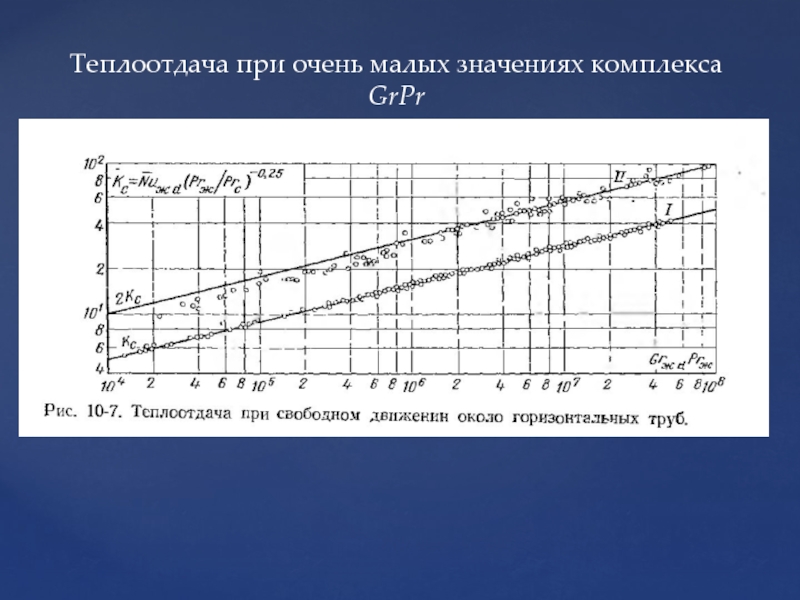
- 83. Теплоотдача при свободном движении около горизонтальной трубы
- 84. Теплоотдача при очень малых значениях комплекса GrPr
- 85. Лекция № 5 Основные законы излучения.
- 86. Описание процесса. виды лучистых потоков, вектор излучения.
- 87. Виды лучистых потока: вектор излучения. Поверхностное (полусферическое)
- 88. Отношение плотности лучистого потока, испускаемого в бесконечном
- 89. Из этих соотношений следует, что Интенсивностью излучения
- 90. Потоки интегрального и монохроматического излучения связаны следующими
- 91. Часть падающей энергии излучения, проходящая сквозь тело,
- 92. В первом способе (Нуссельта) поток результирующего излучения
- 93. если выразить Е эф из способа Власова,
- 94. Объемное излучение Для среды, которая заполняет некоторый
- 95. Лучистые потоки, отнесенные ко всему объему, выразятся
- 96. плотностью эффективного объемного излучения называется суммарная величина
- 97. Вектор излучения. Вектор излучения определяет направление наиболее
- 98. Учитывая, что
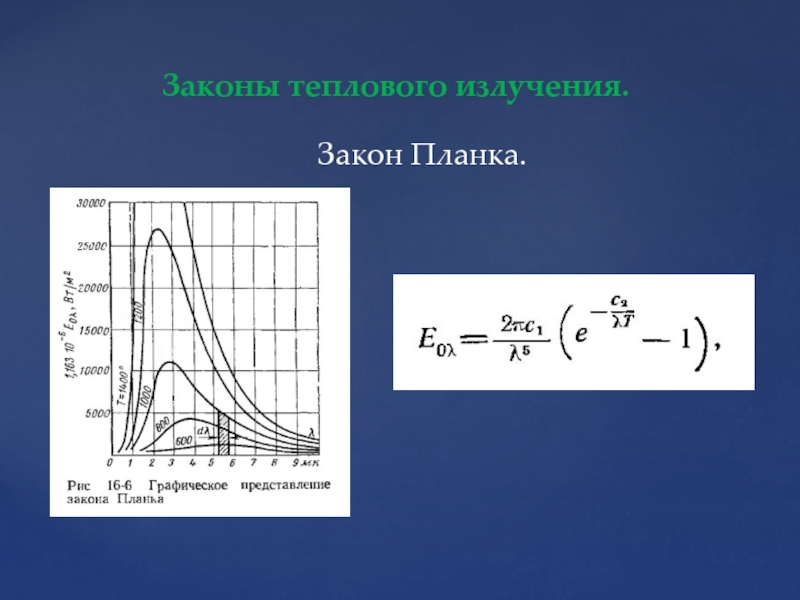
- 99. Законы теплового излучения. Закон Планка.
- 100. Закон Релея-Джинса Переходит в соотношение, выражающее закон Релея-Джинса
- 101. Закон смещения Вина Решение этого уравнения приводит к соотношению Откуда
- 102. Закон Планка в безразмерной форме. Закон
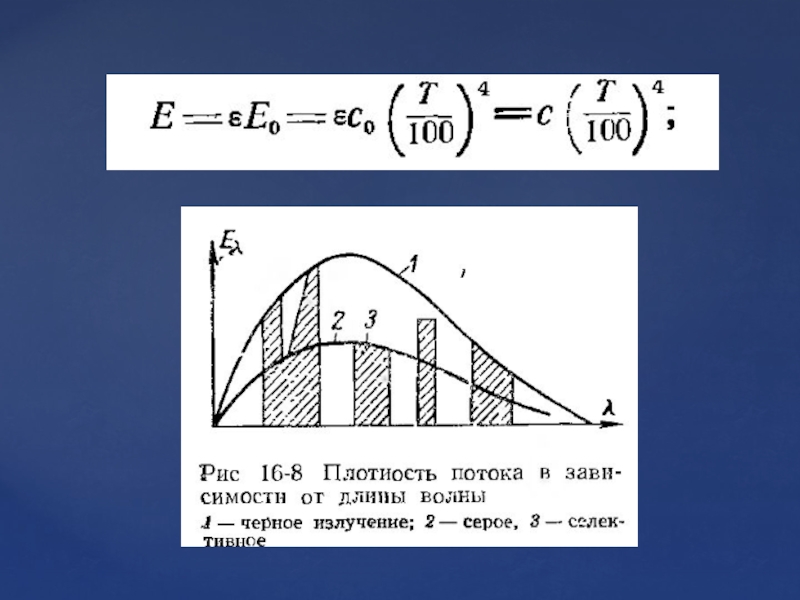
- 103. Закон Стефана — Больцмана
- 105. Закон Кирхгофа
- 106. Закон косинусов Ламберта
- 108. Черные температуры.
Слайд 2Теплопередача или теплообмен — учение о самопроизвольных необратимых процессах распространения теплоты
Слайд 3Методы изучения физических явлений
феноменологический
статистический
Плюсы метода:
-позволяет сразу установить общие связи между параметрами,
-использовать экспериментальные данные, точность которых предопределяет и точность самого метода.
Минусы:
-сложный;
-дорогостоящий.
Плюсы метода:
-позволяет получить феноменологические соотношения на основании заданных свойств микроскопической структуры среды без дополнительного эксперимента.
Минусы:
-сложность;
-требуются знания ряда параметров, для которых требуются знания специальных разделов физики.
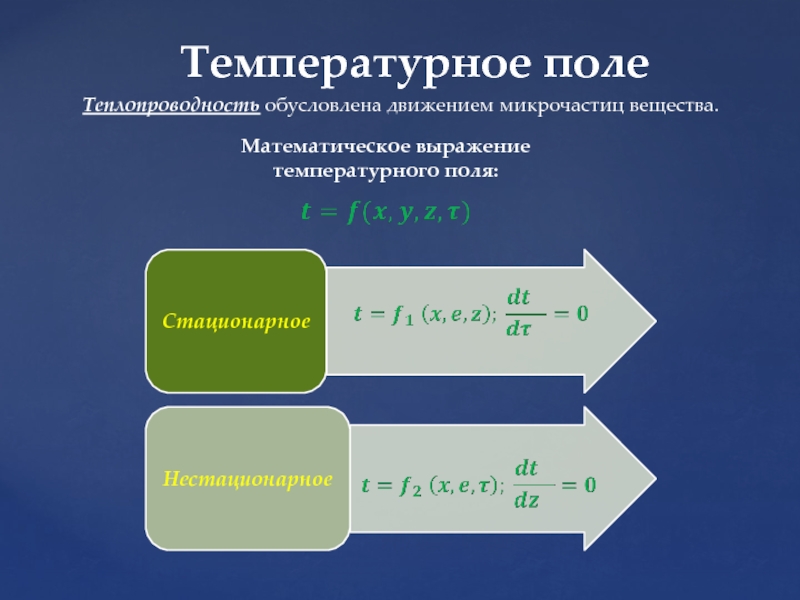
Слайд 4Температурное поле
Теплопроводность обусловлена движением микрочастиц вещества.
Математическое выражение температурного поля:
Слайд 5Уравнение для одномерного поля:
Простой вид уравнения одномерного стационарного температурного поля:
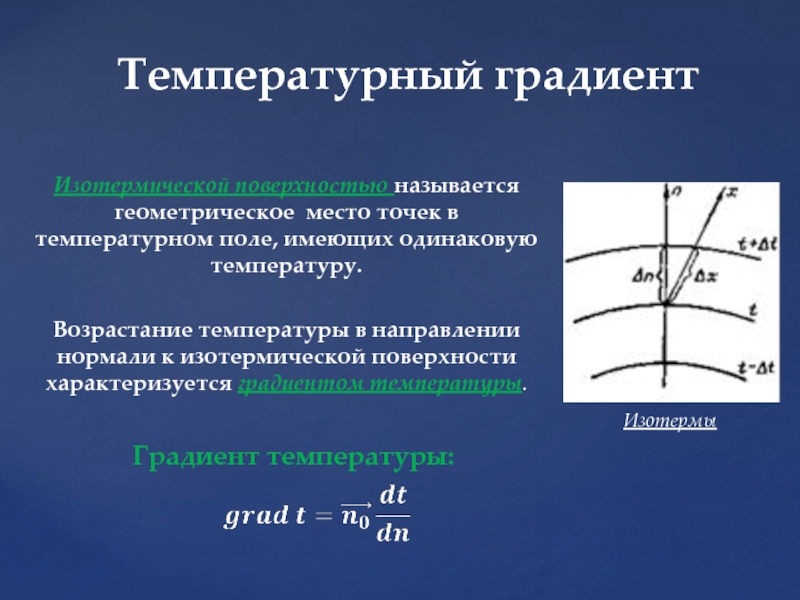
Слайд 6Температурный градиент
Изотермической поверхностью называется геометрическое место точек в температурном поле, имеющих
Изотермы
Возрастание температуры в направлении нормали к изотермической поверхности характеризуется градиентом температуры.
Градиент температуры:
Слайд 8Тепловой поток.
Закон Фурье.
Для передачи теплоты теплопроводностью необходимо неравенство нулю температурного
Гипотеза Фурье:
Плотностью теплового потока:
Слайд 11Коэффициент теплопроводности
Порядок значений коэффициентов теплопроводности различных веществ
Коэффициент теплопроводности,
Вт/(м*К):
Слайд 13Коэффициент теплопроводности жидкости
Коэффициент теплопроводности капельных жидкостей лежит примерно в пределах от
При повышении давления коэффициенты теплопроводности жидкостей возрастают.
Слайд 17Если ограничиться двумя первыми членами ряда, то:
Количество теплоты, отведенное через
Разница количеств теплоты:
или
Количество теплоты dQ:
Т. о.
Функция является непрерывной в рассматриваемом интервале dx и может быть разложена в ряд Тейлора:
Слайд 18Если система тел не содержит внутренних источников тепла (q=0), тогда выражение
Дифференциальное уравнение теплопроводности превращается в уравнение- Пуассона:
Для стационарной теплопроводности и отсутствия внутренних источников теплоты выражение принимает вид уравнения Лапласа:
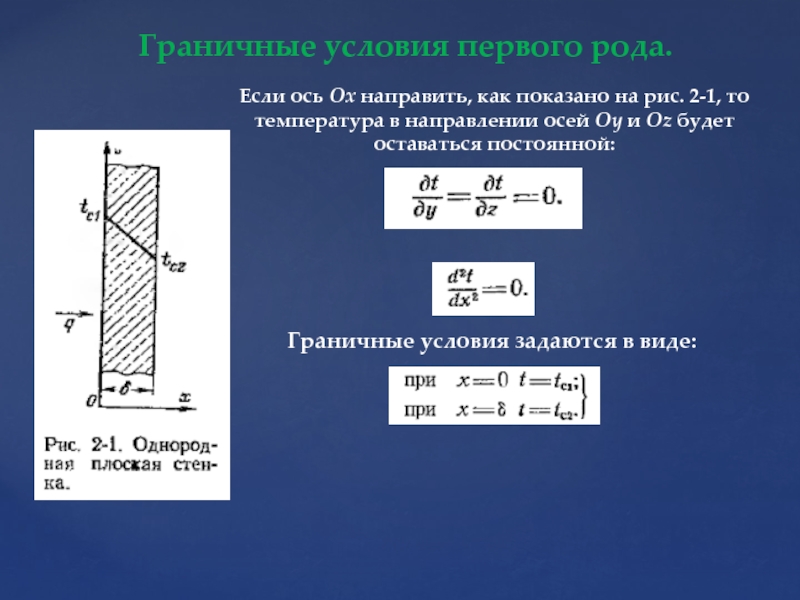
Слайд 21Граничные условия первого рода.
Если ось Ох направить, как показано на
Граничные условия задаются в виде:
Слайд 23Закон распределения температуры:
- текущий температурный напор
- полный температурный напор
- безразмерный температурный
- безразмерная координата
Получим:
Слайд 27Граничные условия третьего рода (теплопередача).
Плотность теплового потока от горячей жидкости
При стационарном тепловом режиме тот же тепловой поток пройдет путем теплопроводности через твердую стенку:
Тот же тепловой поток передается от второй поверхности стенки к холодной жидкости за счет теплоотдачи:
Таким образом получим:
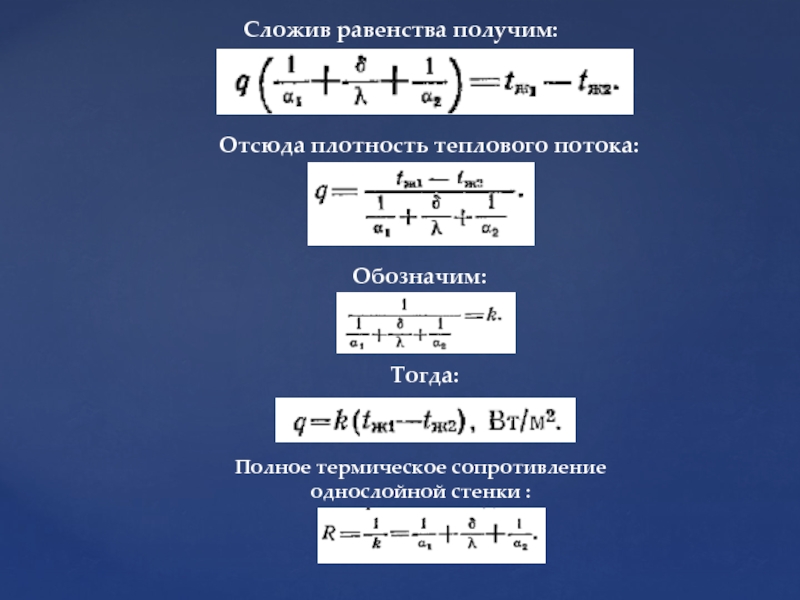
Слайд 28Сложив равенства получим:
Отсюда плотность теплового потока:
Обозначим:
Тогда:
Полное термическое сопротивление однослойной стенки :
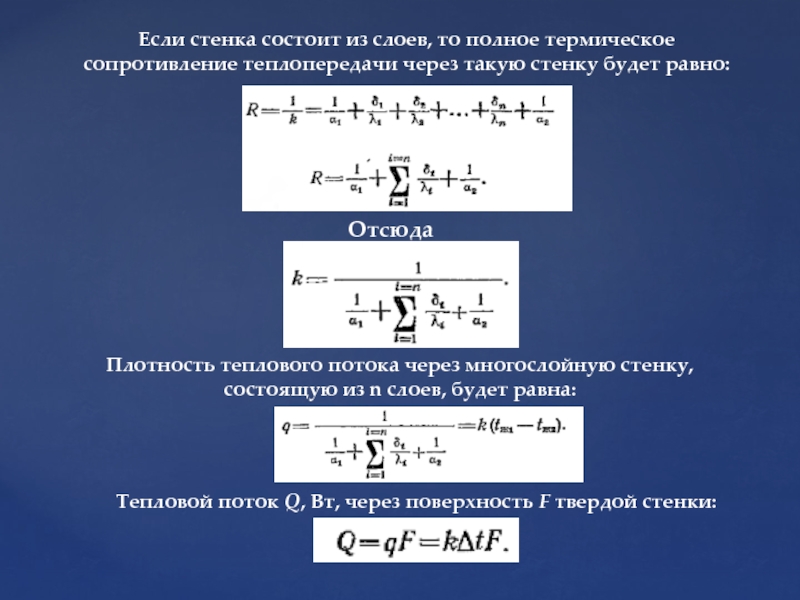
Слайд 29Если стенка состоит из слоев, то полное термическое сопротивление теплопередачи через
Отсюда
Плотность теплового потока через многослойную стенку, состоящую из n слоев, будет равна:
Тепловой поток Q, Вт, через поверхность F твердой стенки:
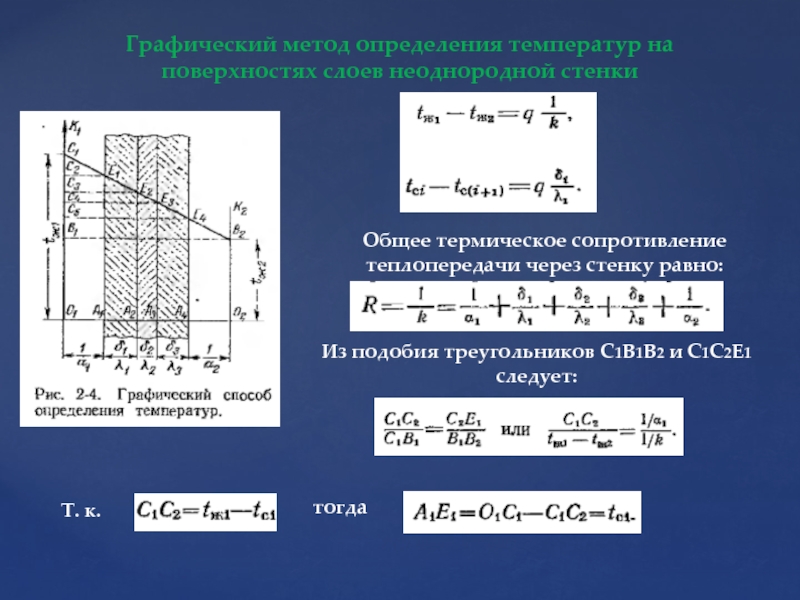
Слайд 31Графический метод определения температур на поверхностях слоев неоднородной стенки
Общее термическое сопротивление
Из подобия треугольников C1B1B2 и C1C2E1 следует:
Т. к.
тогда
Слайд 32Граничные условия второго и третьего рода
В силу стационарности теплового режима можно
на внешней правой поверхности
на внешней левой поверхности
на поверхности между слоями m — 1 и m
Слайд 33Передача теплоты через цилиндрическую стенку
1) Граничные условия первого рода
Цилиндрическая система
Т. к. поле одномерное, то:
Изотермические поверхности являются цилиндрическим, сл-но:
Граничные условия:
Слайд 36Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и
Среднеинтегральное значение:
Уравнение закона Фурье:
Слайд 38Величина ki называется линейным коэффициентом теплопередачи, он измеряется в Вт/ (м
Линейное термическое сопротивление теплопередачи:
Плотность теплового потока:
где
Слайд 39На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению
Если
то
Если стенка тонкая:
Для многих технических расчетов ошибка, не превышающая 4%, вполне допустима Обычно в инженерных расчетах при d2/d1≤1,8 используются формулой.
Ошибку можно уменьшить, если в качестве расчетной поверхности брать поверхность, со стороны которой α меньше:
Слайд 40В случае теплопередачи через многослойную цилиндрическую стенку система равенств должна быть
Слайд 41В случае задания граничных условий первого рода можно рассматривать как предельный
Температура между граничными слоями:
Слайд 42Пути интенсификации теплопередачи
а) Интенсификация теплопередачи путем увеличения коэффициентов теплоотдачи
Из уравнения теплопередачи
Для
Слайд 43Из уравнения видно, что коэффициент теплопередачи не может быть больше α.
Слайд 44б) Интенсификация теплопередачи за счет оребрения стенок
При передаче теплоты через цилиндрическую
Строгое аналитическое решение задачи о распространении тепла в ребре связано со значительными трудностями. В основу решения поэтому кладут некоторые допущения, которые позволяют сравнительно простым путем получить нужный результат. Ниже рассмотрим метод решения задач о теплопроводности в ребрах простейших геометрических форм.
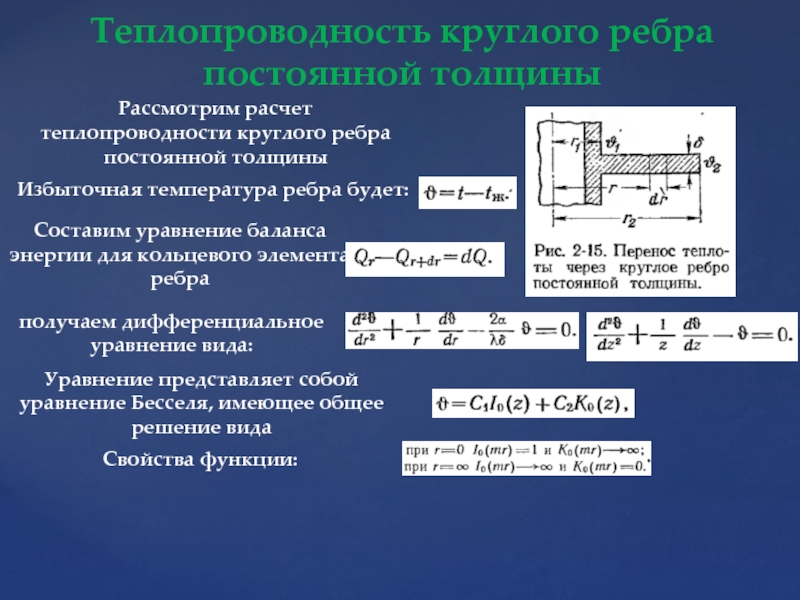
Слайд 45Теплопроводность круглого ребра постоянной толщины
Рассмотрим расчет теплопроводности круглого ребра постоянной толщины
Избыточная температура ребра будет:
Составим уравнение баланса энергии для кольцевого элемента ребра
получаем дифференциальное уравнение вида:
Уравнение представляет собой уравнение Бесселя, имеющее общее решение вида
Свойства функции:
Слайд 46Если температурой с торца круглого ребра пренебречь:
для температуры на конце ребра
для
Количество теплоты, которое будет отдаваться поверхностью круглого ребра постоянной толщины
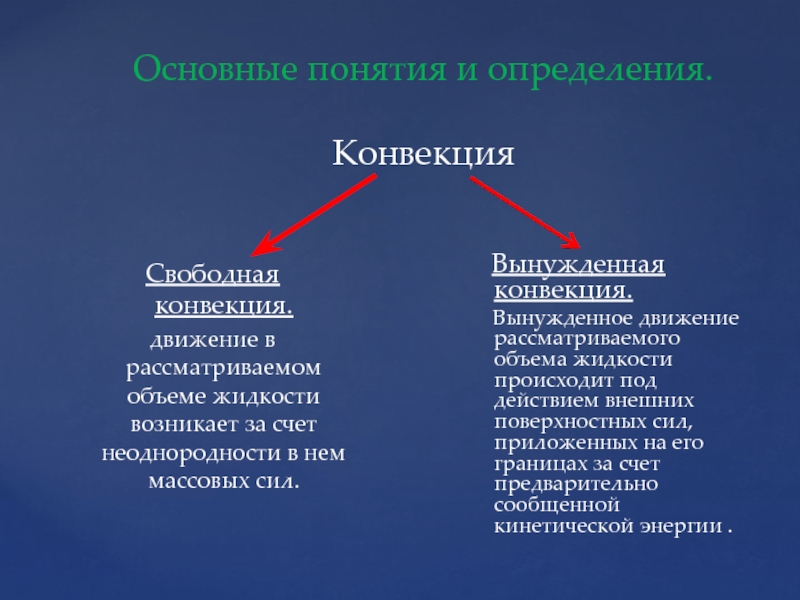
Слайд 48Основные понятия и определения.
Конвекция
Свободная конвекция.
движение в рассматриваемом объеме жидкости возникает за
Вынужденная конвекция.
Вынужденное движение рассматриваемого объема жидкости происходит под действием внешних поверхностных сил, приложенных на его границах за счет предварительно сообщенной кинетической энергии .
Слайд 49Физические свойства жидкости.
Процесс теплообмена зависит от физических свойств жидкостей:
коэффициент теплопроводности Л,
удельная теплоемкость ср,
плотность р,
коэффициент температуропроводности а
коэффициент вязкости μ .
Слайд 50Реальные жидкости обладают вязкостью; между частицами или слоями, движущимися с различными
Согласно закону Ньютона эта касательная сила s, Па
Коэффициент μ называется динамическим коэффициентом вязкости или просто коэффициентом вязкости; его единица измерения Н-с/м2. При
Численно
Слайд 51отношение вязкости μ к плотности р, называемое кинематическим коэффициентом вязкости и
У капельных жидкостей вязкость почти не зависит от давления, но значительно уменьшается при повышении температуры.
Слайд 52
На теплоотдачу оказывает влияние сжимаемость жидкостей. Изотермической сжимаемостью или коэффициентом сжатия
t=const называют величину
Для капельных жидкостей изотермическая сжимаемость чрезвычайно мала. Для воды
Слайд 53Помимо изотермической сжимаемости для конвективного теплообмена большое значение имеет тепловое расширение
Для некоторых жидкостей, например для воды при t<4°С, коэффициент р может иметь отрицательное значение.
Для идеального газа температурный коэффициент объемного расширения есть величина, обратная абсолютной температуре газа,
Слайд 54Дифференциальные уравнения конвективного теплообмена.
Из уравнения:
следует, что плотность теплового потока в
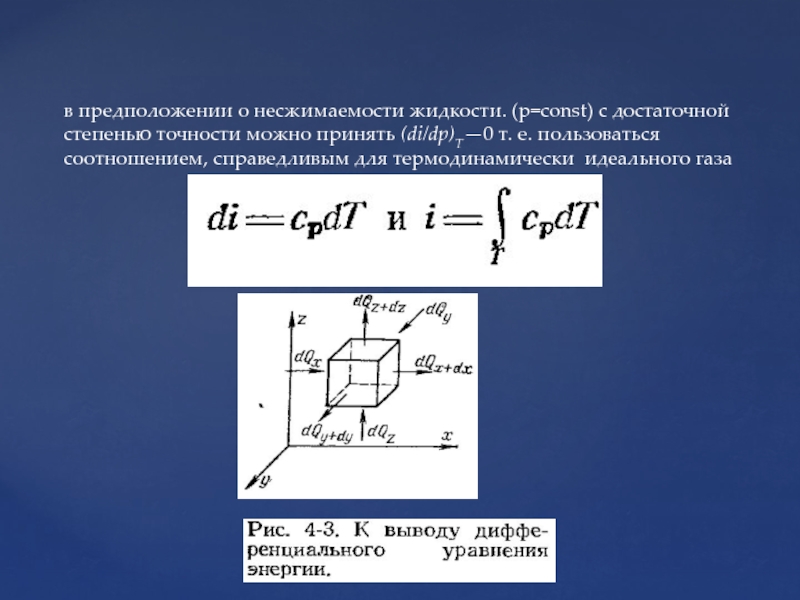
Слайд 56в предположении о несжимаемости жидкости. (р=const) с достаточной степенью точности можно
Слайд 57Вывод уравнения энергии
Где
Согласно уравнению проекции плотности теплового потока q на
Слайд 58Подставляя значений qx, qy и qz в уравнение (1-25), можно получить:
Для
Слайд 60Здесь dt/dx характеризует изменение температуры во времени в какой-либо точке жидкости,
Применяя обозначение
Уравнение энергии можно записать
если
Уравнение энергии переходит в уравнение теплопроводности
Слайд 61При стационарных процессах конвективного теплообмена dt/dт=0.
упрощенный вывод этого уравнения для
Выделим в потоке вязкой жидкости элементарный объем с размерами ребер dx, dy и dz
Вывод уравнения движения основан на втором закона Ньютона: сила равна массе, умноженной на ускорение
Слайд 62Силы, действующие на рассматриваемый элемент жидкости, можно разделить на массовые (или
проекция на ось Ох равна произведению проекции ускорения свободного падения gx на массу элемента:
Если на верхней грани элемента давление жидкости равно р, то на площадку dydz действует сила р dy dz.
На нижней грани давление с точностью до второго члена разложения в ряд Тейлора равно
и на эту грань действует сила
Слайд 63Равнодействующая этих сил равна алгебраической сумме:
Подставляя
получаем
Согласно второму закону механики эта равнодействующая
Суммируя dfi, df2 и dfs, получаем проекцию на ось Ох равнодействующей всех сил, приложенных к объему (а):
Слайд 64Приравнивая правые части уравнений (а) и (б) и производя сокращения, окончательно
трехмерного движения несжимаемой жидкости с постоянными физическими параметрами скоростное поле описывается тремя уравнениями движения, каждое соответственно в проекциях сил на оси Ох, Оу и Oz: для оси Ох
Слайд 65ДЛЯ оси ОY
Для оси OZ
На основании понятия о полной производной имеем:
Аналогично
Слайд 67Основные положения Омывание трубы поперечным неограниченным потоком жидкости характеризуется рядом особенностей. Плавное,
Слайд 69Если учитывается только сила тяжести, то
Свободное движение возникает за счет неоднородного
Такими силами являются:
Сила тяжести;
Центробежная сила;
Сила за счет наведения в жидкости электромагнитного поля высокой напряженности.
Слайд 70Теплоотдача при свободном движении жидкости в большом объеме. Теплоотдача при свободном
Вертикальная пластина с неизменной температурой поверхности равной tc , находится в жидкости или газе. Температура жидкости вдали от пластины постоянна и равна t0.
tc > t0
Слайд 72Для стационарного течения я с учетом ранее принятых допущений уравнение движения
При линейной зависимости плотности от температуры, где
Отсюда
Слайд 73Подставляя значение υ в уравнение и учитывая последнее соотношение для плотности,
Интегрирование уравнения движения дает:
Слайд 74Примем следующие граничные условия для скорости: wx=0 как при у=0, так
Подставив значение C1 и C2 в уравнение и преобразовав получим уравнение распределения скоростей в движущемся слое жидкости:
Максимум скорости соответствует значению:
Слайд 75Среднеинтегральная скорость равна: среднюю температуру жидкости в слое определим приближенно как среднеинтегральную
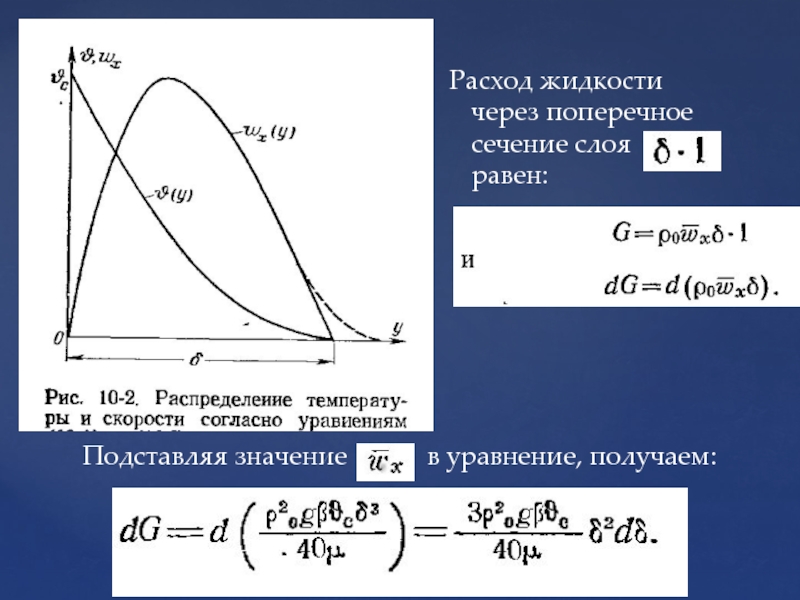
Слайд 76Подставляя значение в уравнение, получаем:
Расход жидкости
Слайд 77Можно считать, что в среднем жидкость нагревается до температуры
Из уравнения (е) следует, что
Приравнивая правые части уравнений , получаем дифференциальное уравнение, описывающее изменение δ по высоте стенки:
Слайд 78Постоянную интегрирования с найдем из условия, что при х=0 δ =0.
Из уравнения следует, что
Согласно уравнению α=2λ/δ
Подставляя сюда значение δ, получаем:
Слайд 79Приведем уравнение к безразмерному виду, для чего левую и правую части
После некоторых преобразований получим:
Из уравнения следует, что .При этом
Слайд 80Для расчета местных коэффициентов при свободном ламинарном течении вдоль вертикальных стенок
Тогда расчетная формула для средних коэффициентов теплоотдачи будет:
Слайд 81Теплоотдача при свободном турбулентном движении вдоль вертикальной пластины
развитое турбулентное течение
.
Для местных коэффициентов теплоотдачи при развитом турбулентном течении в предложена формула:
Линейный размер входит в числа Nu и Gr :
Слайд 82Теплоотдача при переходном режиме свободного движения вдоль вертикальной пластины
переходный режим имеет
Переходный режим отличается неустойчивостью процесса течения и теплоотдачи и, как следствие, большим разбросом опытных точек.
Слайд 86Описание процесса. виды лучистых потоков, вектор излучения.
Тепловое излучение представляет собой
Слайд 87Виды лучистых потока: вектор излучения.
Поверхностное (полусферическое) излучения.
Тело излучает энергию в виде
Или прерывистого спектра по длинам волн.
Интегральный поток, испускаемый с единицы поверхности, носит название поверхностной плотности потока интегрального излучения
Лучистый поток со всей поверхности выразится интегралом:
Слайд 88Отношение плотности лучистого потока, испускаемого в бесконечном малом интервале длин волн,
Количество энергии, испускаемое в определенном направлении /, определяемым углом -ψ с нормалью к поверхности п единицей элементарной площадки в единицу времени в пределах элементарного телесного угла dω, называется угловой плотностью излучения.
Слайд 89Из этих соотношений следует, что
Интенсивностью излучения называется количество лучистой энергии, испускаемое
Слайд 90Потоки интегрального и монохроматического излучения связаны следующими зависимостями:
Плотность потока поглощающей лучистой
Часть падающей энергии, которую поверхность данного тела отражает обратно окружающим его телам, носит название потока отраженного излучения. Плотность потока отраженного излучения E отр, Вт/м2, равна:
Слайд 91Часть падающей энергии излучения, проходящая сквозь тело, называется плотностью потока пропускаемого
Суммарная величина плотностей потоков собственного и отраженного излучения, испускаемого поверхностью данного тела, называется плотностью эффективного излучения:
Слайд 92В первом способе (Нуссельта) поток результирующего излучения определяется из теплового баланса
Второй способ (О. Е. Власова) состоит в определении фрез из баланса относительно воображаемой поверхности б— б, находящейся вне тела, но вблизи его поверхности
В общем случае плотность потока результирующего излучения определяется разностью .встречных потоков излучения, падающих на условную поверхность в — в (Ю. А. Суринов)
Слайд 93если выразить Е эф из способа Власова, а Е пад из
и подставить в способ Суринова, то получим:
Слайд 94Объемное излучение
Для среды, которая заполняет некоторый объем системы и может быть
Интегральной и монохроматической объемными плотностями потоков собственного излучения называются лучистые потоки, испускаемые единицей объема среды в единицу времени по всем различным направлениям в пределах пространственного угла ω=4π:
Слайд 95Лучистые потоки, отнесенные ко всему объему, выразятся зависимостями
Потоки монохроматического и интегрального
Плотность поглощенного объемного излучения
и плотность рассеянного объемного излучения
Слайд 96плотностью эффективного объемного излучения называется суммарная величина плотностей потоков собственного и
плотность потока результирующего объемного излучения выражается зависимостью
Последние две зависимости могут быть использованы для получения уравнений, связывающих плотности потоков результирующего и эффективного объемных излучений, аналогичных
Слайд 97Вектор излучения.
Вектор излучения определяет направление наиболее интенсивного переноса лучистой энергии в
Слайд 98Учитывая, что
Составляющие плотности потока результирующего излучения в направлении осей координат OX OY OZ являются компонентами вектора излучения