общей физики
Трофимова Т.И. Курс физики
Сивухин Д.В. Общий курс физики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы векторной алгебры. Декартовая система координат презентация
Содержание
- 2. Элементы векторной алгебры
- 3. Элементы векторной алгебры
- 4. Элементы векторной алгебры
- 5. Элементы векторной алгебры
- 6. Кинематика Кинематика материальной точки
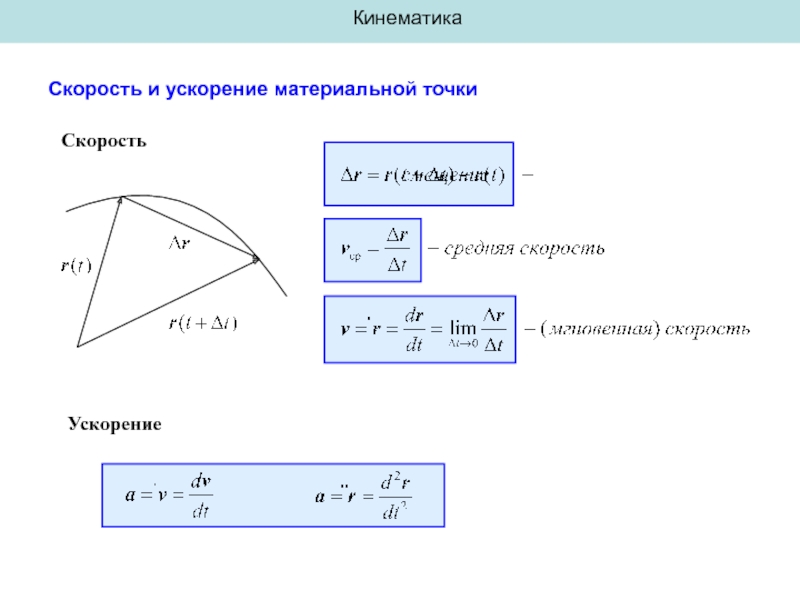
- 7. Кинематика Скорость и
- 8. Кинематика Прямолинейное движение
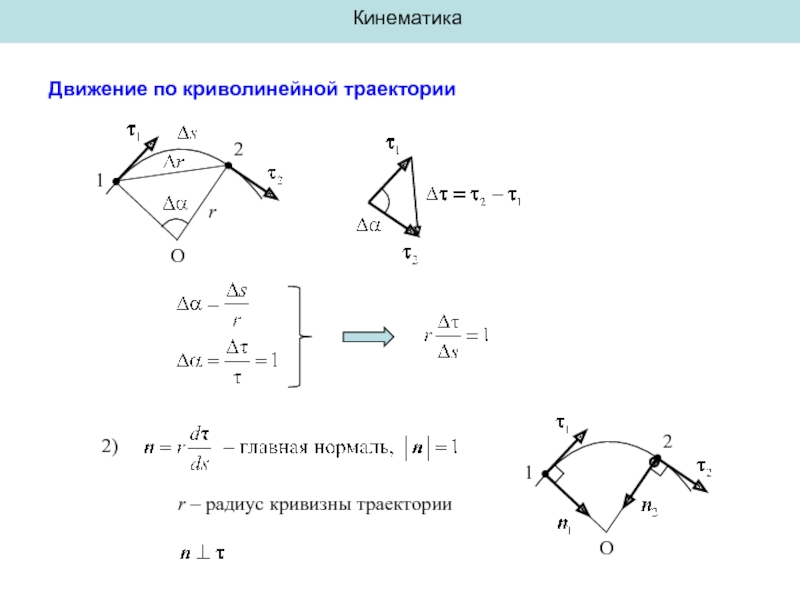
- 9. Кинематика Движение по криволинейной траектории
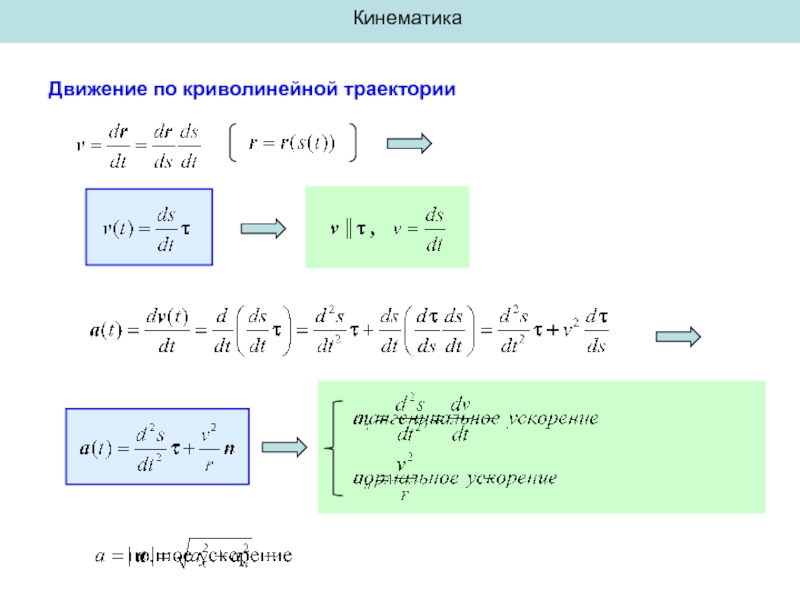
- 10. Кинематика Движение по криволинейной траектории
- 11. Кинематика Движение по
- 12. Кинематика Движение по окружности
- 13. Кинематика Движение по окружности
- 14. Кинематика Движение по окружности
Элементы векторной алгебры Декартовая система координат x, y, z – координаты (⋅)A r – радиус-вектор r = x⋅i + y⋅j + z⋅k
Слайд 1
ФИЗИКА
ЛИТЕРАТУРА:
Иродов И.Е. Общая физика
Матвеев А.Н. Курс физики
Джанколи Д. Физика
Савельев И.А. Курс
Слайд 2Элементы векторной алгебры
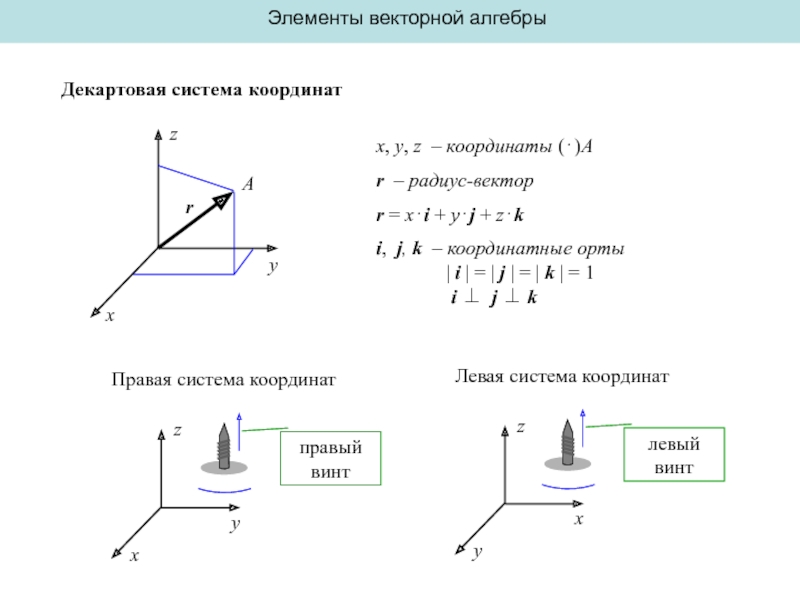
Декартовая система координат
x, y, z – координаты (⋅)A
r
– радиус-вектор
r = x⋅i + y⋅j + z⋅k
i, j, k – координатные орты | i | = | j | = | k | = 1 i ⊥ j ⊥ k
r = x⋅i + y⋅j + z⋅k
i, j, k – координатные орты | i | = | j | = | k | = 1 i ⊥ j ⊥ k
x
y
z
Правая система координат
правый
винт
x
z
Левая система координат
левый
винт
y
Слайд 3
Элементы векторной алгебры
Обозначение вектора:
A, B, C
Определение вектора: вектор – упорядоченный набор
чисел.
A ≡ (Ax, Ay, Az), Ai (i = x, y, z) – составляющие (компоненты) вектора
A ≡ (Ax, Ay, Az), Ai (i = x, y, z) – составляющие (компоненты) вектора
Сложение векторов и умножение вектора на число
Сложение по правилу
параллелограмма
B
A
A+B
Сложение по правилу
треугольника
B
A
A+B
Слайд 4
Элементы векторной алгебры
Сложение нескольких векторов
С
A
A+B+С
B
Скалярное произведение
A
B
BA
В декартовой системе координат
α
Слайд 5
Элементы векторной алгебры
Векторное произведение
B
С = [A, B]
В декартовой системе координат
α
A
правый
винт
A
B
1)
2)
Слайд 6
Кинематика
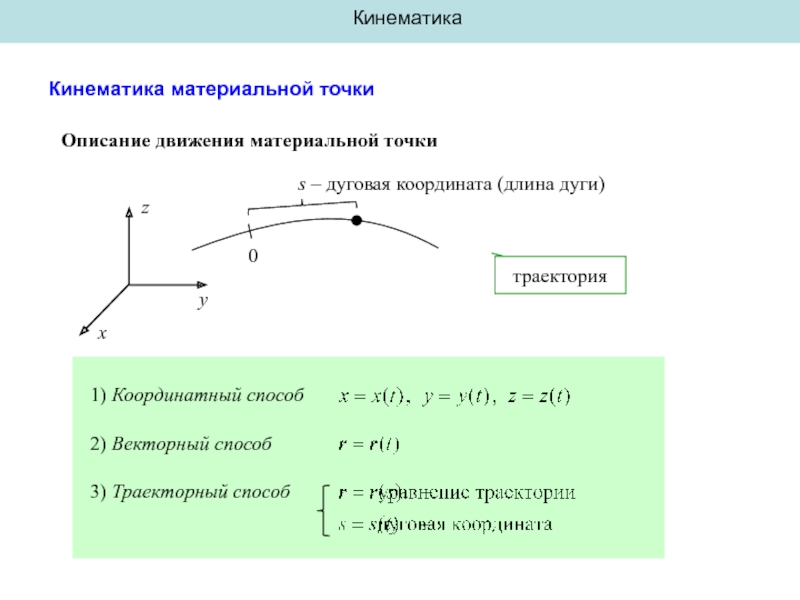
Кинематика материальной точки
1) Координатный способ
2) Векторный способ
3) Траекторный
способ
x
y
z
траектория
0
s – дуговая координата (длина дуги)
Описание движения материальной точки
Слайд 8
Кинематика
Прямолинейное движение
0
x(t)
x
1) Равномерное движение,
2) Равноускоренное движение,
x0 – начальные координата
v0 – начальная
скорость
Слайд 13
Кинематика
Движение по окружности
ϕ
2) Равноускоренное вращение,
x
Связь линейный и угловых величин
r
Слайд 14
Кинематика
Движение по окружности
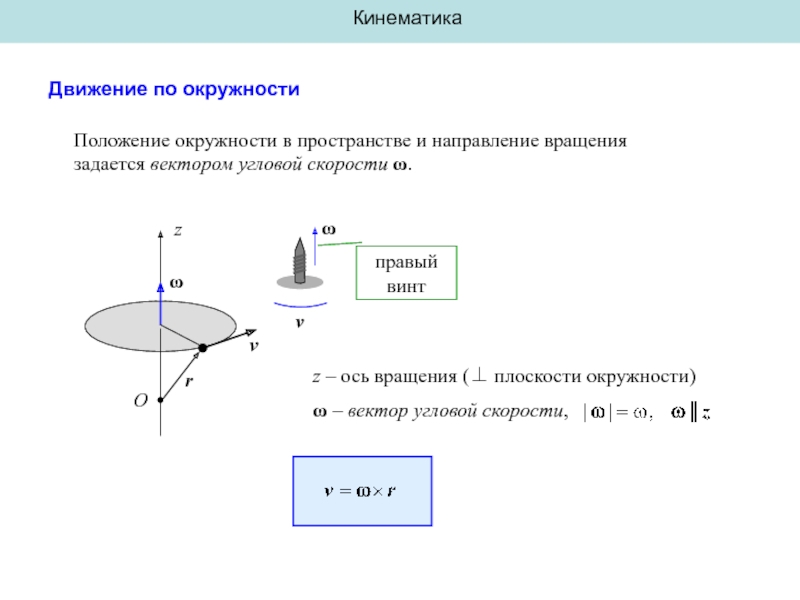
Положение окружности в пространстве и направление вращения задается вектором
угловой скорости ω.
z
r
O
ω
v
правый
винт
ω
v
z – ось вращения (⊥ плоскости окружности)
ω – вектор угловой скорости,
