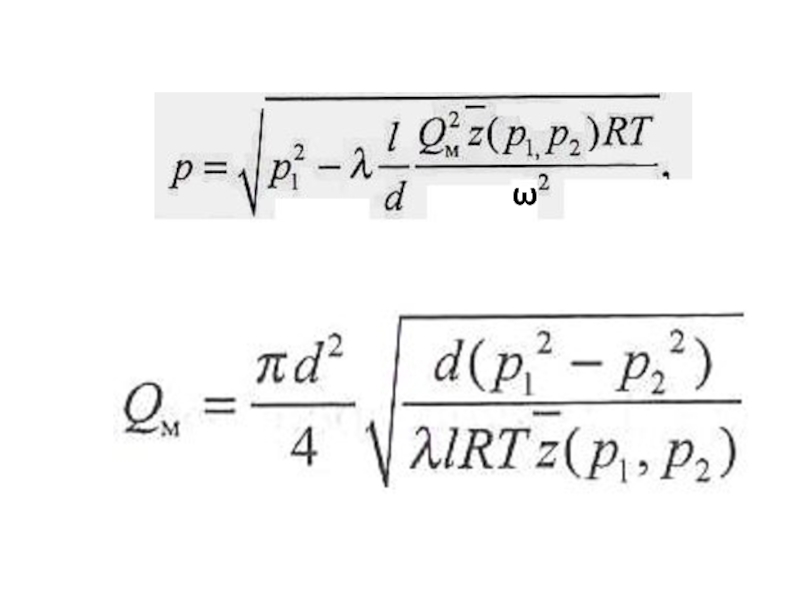- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы механики газа презентация
Содержание
- 1. Элементы механики газа
- 2. Влияние на плотность газа температуры и давления
- 3. р - абсолютное давление; R - удельная
- 4. В технических расчетах плотность газа обычно при-водят
- 5. Для адиабатического процесса Влияние на плотность
- 6. Важной характеристикой, определяющей зависимость изменения плотности при
- 7. Так как объем
- 8. Если жидкость или газ движется, то
- 9. При большой высоте столба воздуха плотность его
- 10. Равновесие газа Рассматривая дифференциальное уравнение дав- ления
- 11. Для отдельных слоев атмосферы с достаточной точностью
- 12. Равновесие газа Значения коэффициента α на разных
- 13. Равновесие газа Подставляя в дифференциальное уравнение
- 14. В результате этих действий получается барометри-ческая формула
- 15. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ Закон сохранения
- 16. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ Для магистральных газопроводов поэтому для массового расхода можно записать формулу
- 17. УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ При n
- 18. При движении реальных углеводородных газов для изотермического
Слайд 2Влияние на плотность газа температуры и давления
Газы, в отличие от капельных
Наиболее простыми свойствами обладает газ, разре-женный настолько, что взаимодействие между его молекулами может не учитываться. Это идеальный (совершенный) газ, для которого справедливо уравнение Менделеева-Клапейрона:
Слайд 3р - абсолютное давление;
R - удельная газовая постоянная, различная для разных
Т - абсолютная температура.
Поведение реальных газов в условиях, далеких от сжижения, лишь незначительно отличается от пове-дения совершенных газов, и для них в широких пре-делах можно пользоваться уравнениями состояния совершенных газов.
Влияние на плотность газа температуры и давления
Слайд 4В технических расчетах плотность газа обычно при-водят к нормальным физическим условиям:
Плотность воздуха при других условиях определя-
ется по формуле:
Влияние на плотность газа температуры и давления
Слайд 5Для адиабатического процесса
Влияние на плотность газа температуры и давления
По данной
k=ср /сv адиабатическая постоянная газа;
ср - теплоемкость, газа при постоянном давлении;
сv - то же, при постоянном объеме.
Адиабатический процесс – это процесс, про-
текающий без внешнего теплообмена.
Слайд 6Важной характеристикой, определяющей зависимость изменения плотности при изменении давления в движущемся
нения звука определяется из выражения:
Влияние на плотность газа температуры и давления
Для воздуха а= 330 м/с; для углекислого газа 261м/с.
Слайд 7 Так как объем газа в большой мере
3начительные разности давлений, вызывающие существенное изменение плотности газов, могут возникнуть при их движении с большими скоростя-
ми. Соотношение между скоростью движения и скоростью звука в ней позволяет судить о необхо-димости учета сжимаемости в каждом конкретном случае.
Влияние на плотность газа температуры и давления
Слайд 8
Если жидкость или газ движется, то для оценки сжи-маемости пользуются не
Если число Маха значительно меньше единицы, то капельную жидкость или газ можно считать практически несжимаемым
М = ν/а
Влияние на плотность газа температуры и давления
Слайд 9При большой высоте столба воздуха плотность его в различных точках уже
нение гидростатики в этом случае не применяется.
Равновесие газа
При малой высоте столба газа его плотность можно считать одинаковой по высоте столба: тогда давле-
ние, создаваемое этим столбом, определяют по основному уравнению гидростатики.
Слайд 10Равновесие газа
Рассматривая дифференциальное уравнение дав-
ления для случая абсолютного покоя и подставляя
Для того, чтобы проинтегрировать это уравнение, необходимо знать закон изменения температуры воздуха по высоте столба воздуха.
Выразить изменение температуры простой функцией высоты или давления нe представляется возможным, поэтому решение уравнения может быть только приближенным.
Слайд 11Для отдельных слоев атмосферы с достаточной точностью можно принять, что изменение
Т = Т0 +αz,
Равновесие газа
где Т и Т0- абсолютная температура воздуха соответ-ственно на высоте (глубине) z и на поверхности земли, α- температурный градиент, характеризующий изменение температуры воздуха при увеличении высоты(-α) или глубины (+α) на 1 м, К/м.
Слайд 12Равновесие газа
Значения коэффициента α на разных участках по вы-соте в атмосфере
При определении температуры в пределах тропо-сферы (т. е. до 11000 м) обычно принимают
α = 0,0065 K/м, для глубоких шахт среднее значение α принимают, равным 0,004÷0,006 K/м для сухих стволов, для мокрых - 0,01.
Слайд 13Равновесие газа
Подставляя в дифференциальное уравнение давле-ния формулу изменения температуры,
и интегрируя
Уравнение решается относительно Н, заменяя нату-ральные логарифмы десятичными, α - его значением из уравнения через температуру, R - значением для воздуха, равным 287Дж/ (кг·К); и подставляем
g = 9,81 м/с2.
Слайд 14В результате этих действий получается барометри-ческая формула
Равновесие газа
Н = 29,3(Т-Т0)(lg
а также формула для определения давления
где n определяется по формуле
Слайд 15УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ
Закон сохранения энергии в механической форме для
Здесь потери удельной энергии на трение взяты по формуле Дарси-Вейсбаха
Для политропического процесса с постоянным пока-зателем политропы n = const и в предположении, что λ= const после интегрирования получается закон распределения давления вдоль газопровода
Слайд 16УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ
Для магистральных газопроводов
поэтому для массового расхода можно
Слайд 17УСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ГАЗОВ В ТРУБАХ
При n = 1 формулы справедливы для
гося изотермического течения газа.
Коэффициент гидравлического сопротивления λ для газа в зависимости от числа Рейнольдса можно вычислить по формулам, используемым при течении жидкости.
Слайд 18При движении реальных углеводородных газов для изотермического процесса используется уравнение состояния
где
дородных газов определяется по эксперименталь-
ным кривым или аналитически - по приближенным уравнениям состояния.