- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электротехника и электроника. Однофазные электрические цепи синусоидального тока. (Лекция 2) презентация
Содержание
- 1. Электротехника и электроника. Однофазные электрические цепи синусоидального тока. (Лекция 2)
- 2. Параметры синусоидальных электрических величин Синусоидальная функция является
- 3. Аналитические выражения синусоидальных величин Мгновенное значение ЭДС
- 4. Начальные фазы синусоидальных величин Знак «+» или
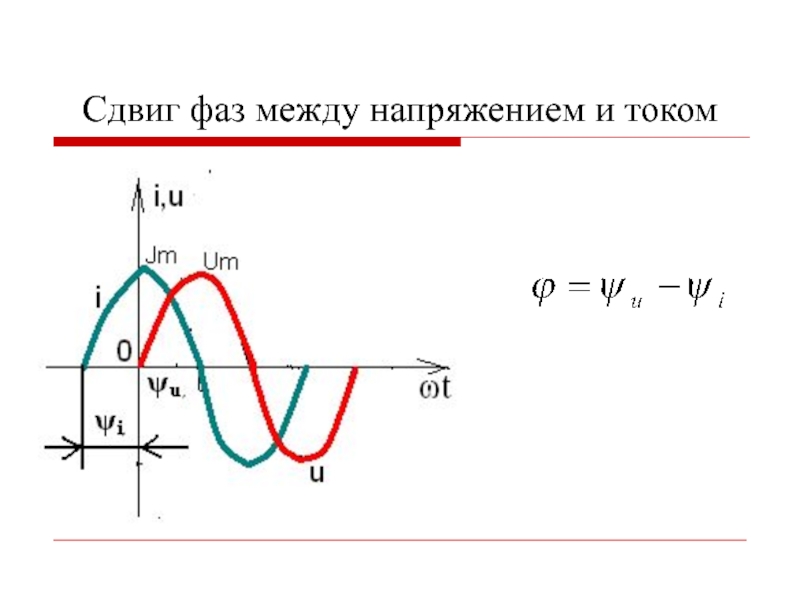
- 5. Сдвиг фаз между напряжением и током
- 6. Действующие и средние значения Расчет действующих значений Расчет среднего значения
- 7. Применение комплексных чисел для расчета электрических цепей
- 8. Применение комплексных чисел для расчета электрических цепей Амплитудные значения Действующие значения
- 9. Правила перехода из одной формы в другую
- 10. Правила перехода из одной формы в другую
- 11. Простейшие математические операции с комплексными числами Сложение и вычитание: Умножение и деление:
- 12. Простейшие математические операции с комплексными числами Единичные
- 13. Комплексное сопротивление Комплексное сопротивление: Модуль комплексного сопротивления:
- 14. Треугольник сопротивлений В алгебраической форме Z=R+jX,
- 15. Мощности в цепях переменного тока Полная мощность: Комплексное действующее значение напряжения: Сопряженный комплекс тока:
- 16. Мощности в цепях переменного тока в алгебраической
- 17. Электрическая цепь с R,L,C-элементами Для каждого
- 18. R-элемент Начальная фаза Угол сдвига фаз
- 19. Полное комплексное сопротивление R-элемента Комплексное сопротивление резистивного
- 20. Мощность на R-элементе На резистивном элементе полная
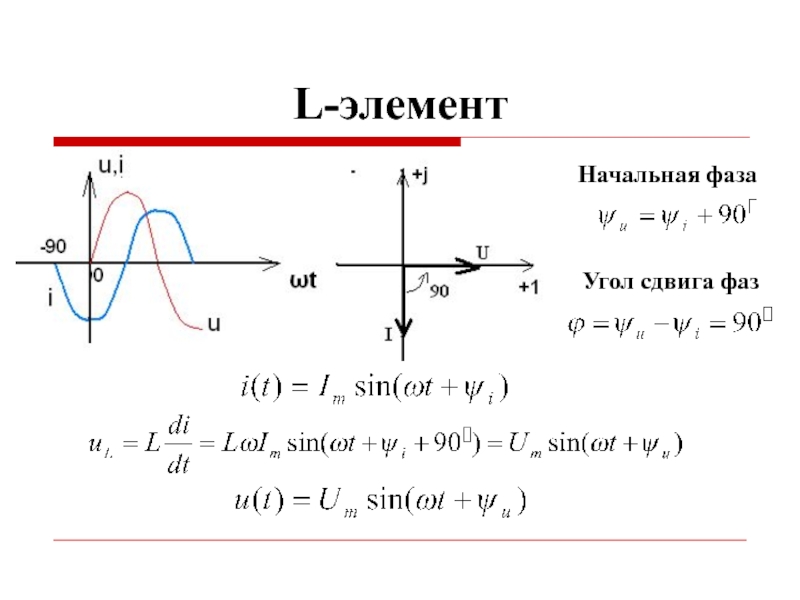
- 21. L-элемент Начальная фаза Угол сдвига фаз
- 22. Полное комплексное сопротивление L-элемента Комплексное сопротивление L-элемента
- 23. Мощность на L-элементе На L–элементе происходит обмен
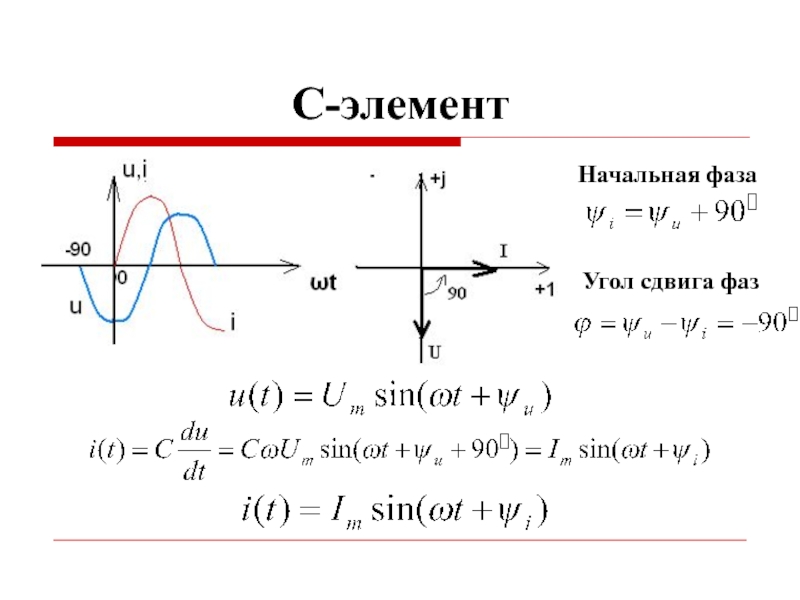
- 24. C-элемент Начальная фаза Угол сдвига фаз
- 25. Полное комплексное сопротивление C-элемента Комплексное
- 26. Мощность на C-элементе На C–элементе происходит обмен
- 27. Анализ цепей синусоидального тока Анализ цепей синусоидального
- 28. Правила построения векторных диаграмм Если электрическая цепь
- 29. Правила построения векторных диаграмм φR=0 φL=90 φC=-90
- 30. Правила построения векторных диаграмм Если электрическая цепь содержит активно-индуктивную нагрузку, то угол 0
- 31. Правила построения векторных диаграмм Если электрическая цепь
- 32. Последовательное соединение элементов в цепи синусоидального тока. Закон Ома:
- 33. Треугольник сопротивлений
- 34. Треугольники напряжений Если XL>XC то отсюда следует
- 35. Треугольники напряжений Если XL
- 36. Резонанс напряжений Режим работы RLC цепи,
- 37. Признаки резонанса напряжений Напряжение на входе совпадает
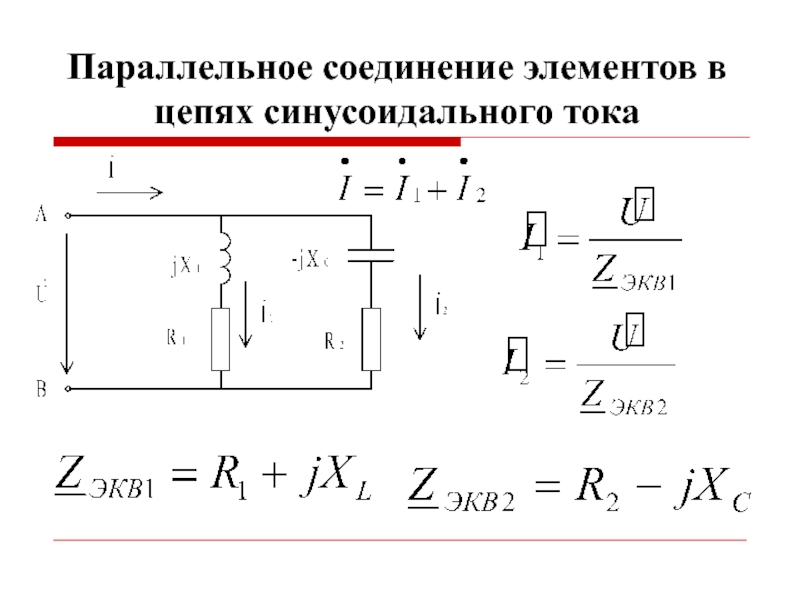
- 38. Параллельное соединение элементов в цепях синусоидального тока
- 39. Треугольники проводимостей
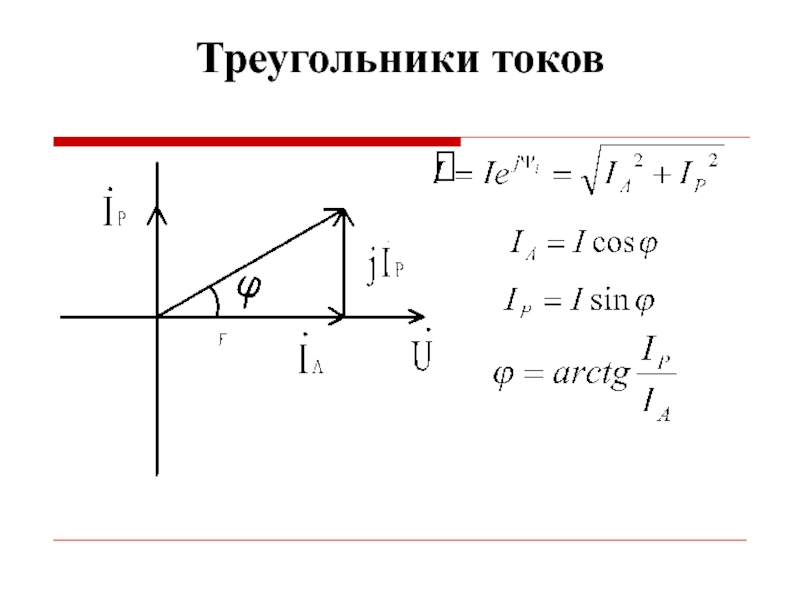
- 40. Треугольники токов
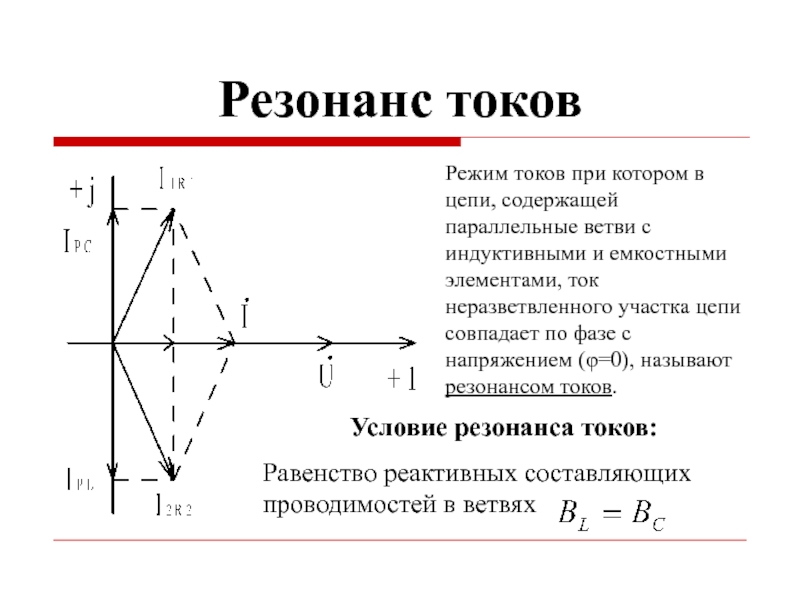
- 41. Резонанс токов
- 42. Признаки резонанса токов Токи ветвей равны
- 43. Частотные характеристики цепей синусоидального тока R –
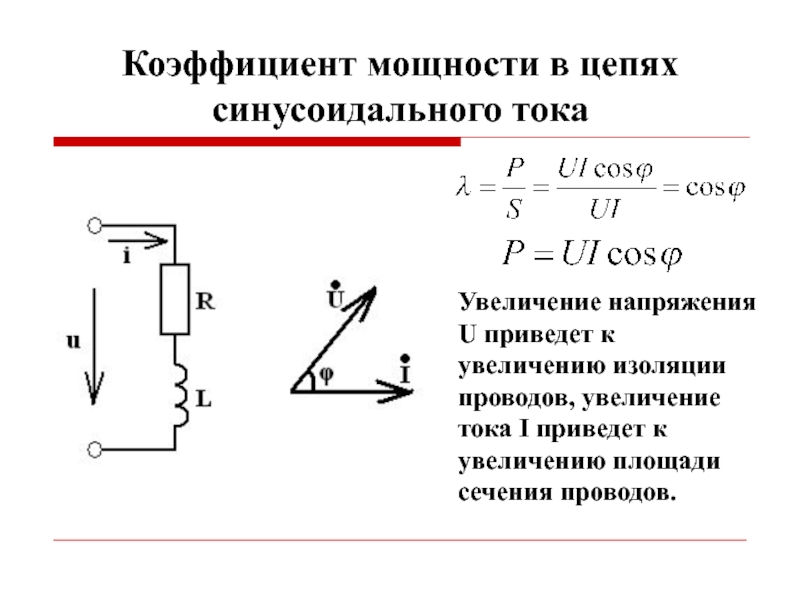
- 44. Коэффициент мощности в цепях синусоидального тока
- 45. Повышение коэффициента мощности в цепях синусоидального тока
Параметры синусоидальных электрических величин Синусоидальная функция является периодической функцией времени, т.е. через равный промежуток времени, называемый периодом T, цикл колебаний повторяется Периоду Т соответствует фазовый угол 2π или 360° Величина
Слайд 2Параметры синусоидальных электрических величин
Синусоидальная функция является периодической функцией времени, т.е. через
равный промежуток времени, называемый периодом T, цикл колебаний повторяется
Периоду Т соответствует фазовый угол 2π или 360°
Величина обратная периоду Т называют частотой и измеряется в Гц
Угловая частота показывает насколько фазовый угол синусоиды изменился за период
Периоду Т соответствует фазовый угол 2π или 360°
Величина обратная периоду Т называют частотой и измеряется в Гц
Угловая частота показывает насколько фазовый угол синусоиды изменился за период
Слайд 3Аналитические выражения синусоидальных величин
Мгновенное значение ЭДС
Мгновенное значение напряжения
Мгновенное значение тока
Im, Um,
Em - амплитудные значения тока, напряжения и ЭДС
(ωt+ψ)- аргумент синуса, который определяют фазовый угол синусоидальной функции в данный момент времени t (фаза)
Ψ – начальная фаза
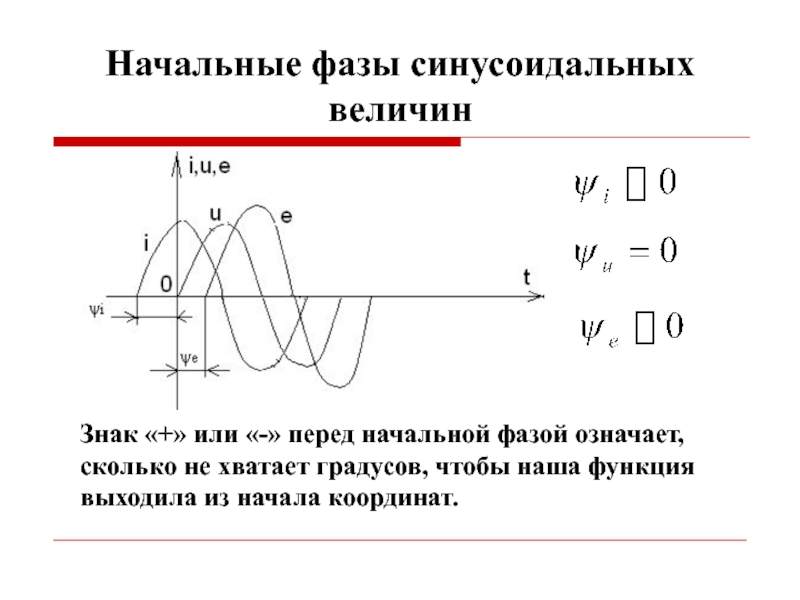
Слайд 4Начальные фазы синусоидальных величин
Знак «+» или «-» перед начальной фазой означает,
сколько не хватает градусов, чтобы наша функция выходила из начала координат.
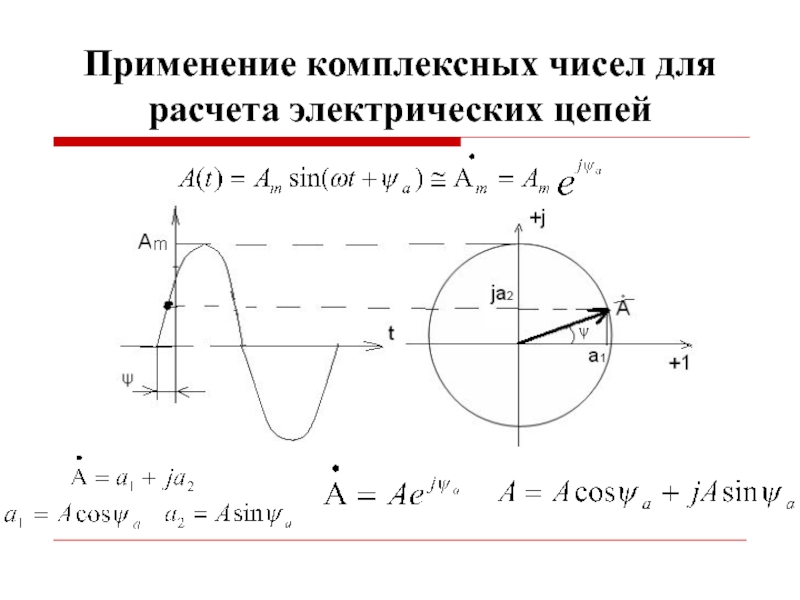
Слайд 8Применение комплексных чисел для расчета электрических цепей
Амплитудные значения
Действующие значения
Слайд 9Правила перехода из одной формы в другую
Из показательной в алгебраическую
Формула Эйлера:
Результат:
Слайд 10Правила перехода из одной формы в другую
Из алгебраической в показательную
Длина вектора
А:
Угол между вектором и осью:
Слайд 11Простейшие математические операции с комплексными числами
Сложение и вычитание:
Умножение и деление:
Слайд 13Комплексное сопротивление
Комплексное сопротивление:
Модуль комплексного
сопротивления:
Комплексное сопротивление
через действующие значения:
Закон Ома для амплитудных значений:
Закон
Ома для действующих значений:
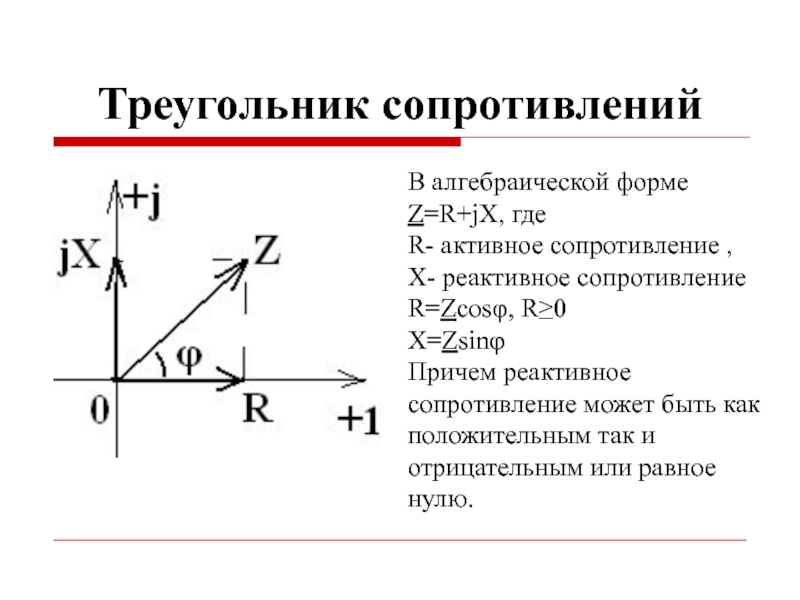
Слайд 14Треугольник сопротивлений
В алгебраической форме Z=R+jX, где
R- активное сопротивление ,
X- реактивное
сопротивление
R=Zcosφ, R≥0
X=Zsinφ
Причем реактивное сопротивление может быть как положительным так и отрицательным или равное нулю.
R=Zcosφ, R≥0
X=Zsinφ
Причем реактивное сопротивление может быть как положительным так и отрицательным или равное нулю.
Слайд 15Мощности в цепях переменного тока
Полная мощность:
Комплексное действующее значение напряжения:
Сопряженный комплекс тока:
Слайд 16Мощности в цепях переменного тока в алгебраической форме
Активная мощность:
Реактивная мощность:
(ВА –вольт-ампер)
(Вт
– ватт)
(ВАр – вольт-ампер реактивный)
Слайд 17Электрическая цепь с
R,L,C-элементами
Для каждого элемента необходимо определить:
Угол сдвига фаз между
напряжением и током (угол φ), построить векторную диаграмму
Полное комплексное сопротивление (Z)
Энергетическую характеристику цепи (P, Q, S)
Полное комплексное сопротивление (Z)
Энергетическую характеристику цепи (P, Q, S)
Слайд 19Полное комплексное сопротивление R-элемента
Комплексное сопротивление резистивного элемента всегда является действительным положительным
числом, которое равно значению активного сопротивления R.
Закон Ома:
Слайд 20Мощность на R-элементе
На резистивном элементе полная мощность равна активной мощности. Это
означает, что на резисторе совершается работа по преобразованию электрической энергии в другие виды энергии.
Слайд 22Полное комплексное сопротивление L-элемента
Комплексное сопротивление L-элемента всегда является мнимым положительным числом,
модуль которого равен ХL.
Реальная катушка имеет активное сопротивление, определяемое сопротивлением проводов, поэтому полное комплексное сопротивление равно:
Реальная катушка имеет активное сопротивление, определяемое сопротивлением проводов, поэтому полное комплексное сопротивление равно:
Закон Ома:
Слайд 23Мощность на L-элементе
На L–элементе происходит обмен энергией между источником электрической энергии
и магнитным полем катушки, что определяет реактивную мощность Q.
Слайд 25Полное комплексное сопротивление C-элемента
Комплексное сопротивление C-элемента всегда является мнимым отрицательным числом,
модуль которого равен ХС.
Следовательно сопротивление конденсатора чисто реактивное и равно:
Следовательно сопротивление конденсатора чисто реактивное и равно:
Закон Ома:
Слайд 26Мощность на C-элементе
На C–элементе происходит обмен энергией между источником электрической энергии
и электрическим полем конденсатора, что определяет реактивную мощность Q. С-элемент работы не совершает, поэтому активная мощность равна 0.
Слайд 27Анализ цепей синусоидального тока
Анализ цепей синусоидального тока происходит при условии, что
все элементы цепи идеальны, т.е. R, L, C идеальны.
Электрическое состояние цепей синусоидального тока описывается теми же законами, что и в цепях постоянного тока.
Электрическое состояние цепей синусоидального тока описывается теми же законами, что и в цепях постоянного тока.
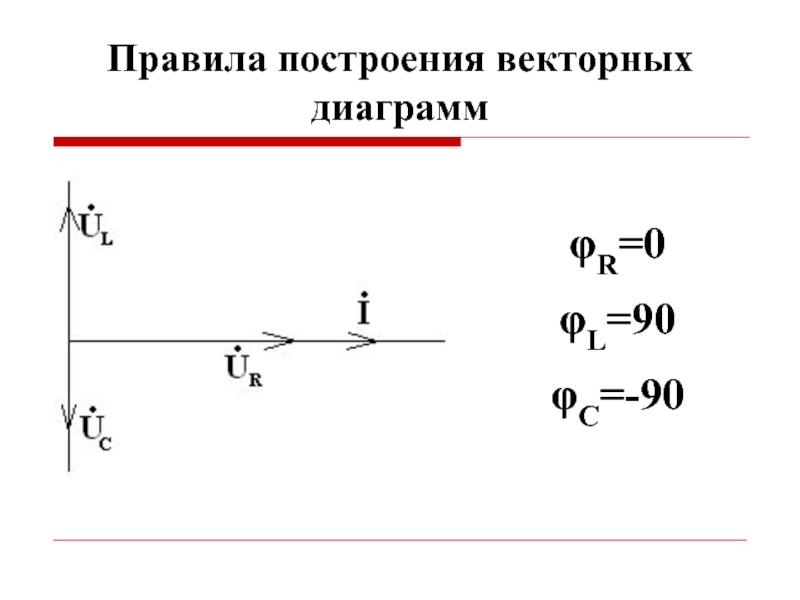
Слайд 28Правила построения векторных диаграмм
Если электрическая цепь содержит идеализированный R элемент, то
угол φ=0 и векторная диаграмма имеет вид
Если электрическая цепь содержит идеализированный L элемент, то угол φ=90 и векторная диаграмма имеет вид
Если электрическая цепь содержит идеализированный C элемент, то угол φ=-90 и векторная диаграмма имеет вид
Слайд 30Правила построения векторных диаграмм
Если электрическая цепь содержит активно-индуктивную нагрузку, то угол
0<φ<90 и векторная диаграмма имеет вид:
Если электрическая цепь содержит активно-емкостную нагрузку, то угол -90<φ<0 и векторная диаграмма имеет вид:
Слайд 31Правила построения векторных диаграмм
Если электрическая цепь содержит последовательное соединение элементов, то
за основу векторной диаграммы принимается вектор тока, относительно которого строятся вектора напряжений.
Если электрическая цепь содержит параллельное соединение элементов, то за основу векторной диаграммы принимается вектор напряжения, относительно которого строятся вектора токов.
Если электрическая цепь содержит параллельное соединение элементов, то за основу векторной диаграммы принимается вектор напряжения, относительно которого строятся вектора токов.
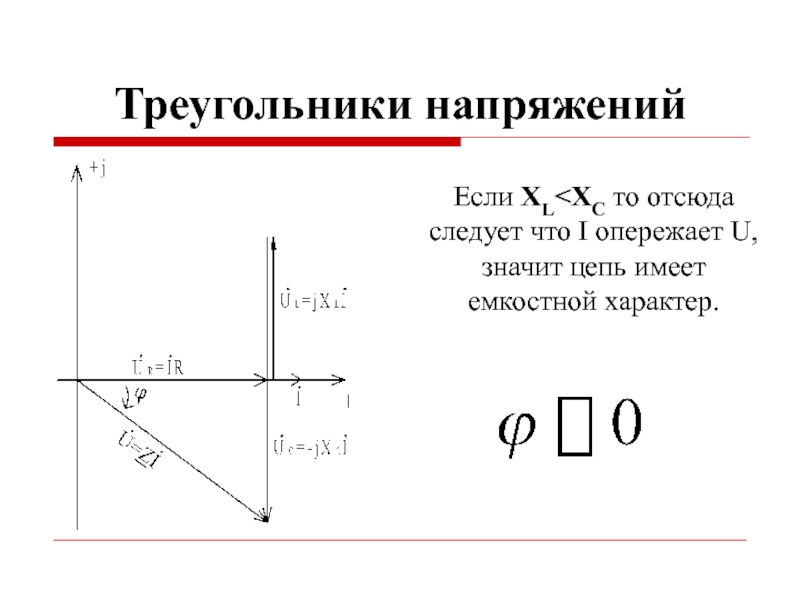
Слайд 34Треугольники напряжений
Если XL>XC то отсюда следует что U опережает I, значит
цепь имеет индуктивный характер.
Слайд 36Резонанс напряжений
Режим работы RLC цепи, при условии равенства реактивных сопротивлений XC=XL,
когда общее напряжение цепи совпадает по фазе с её током φ=0 - называется резонансом напряжений.
Цепь имеет активный характер:
Цепь имеет активный характер:
Слайд 37Признаки резонанса напряжений
Напряжение на входе совпадает по фазе с током, т.е.
сдвиг фаз между I и U φ=0, cos(φ)=1
Ток в цепи будет наибольшим и как следствие Pmax=I2maxR тоже максимальна, а реактивная мощность равна нулю.
Напряжения на элементах цепи могут в несколько раз превышать напряжение на входе
.
Ток в цепи будет наибольшим и как следствие Pmax=I2maxR тоже максимальна, а реактивная мощность равна нулю.
Напряжения на элементах цепи могут в несколько раз превышать напряжение на входе
.
Слайд 39Треугольники проводимостей
G – действительная часть, активная составляющая
B – мнимая часть, реактивная
составляющая
Слайд 41Резонанс токов
Режим токов при котором в цепи, содержащей параллельные ветви с
индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Условие резонанса токов:
Равенство реактивных составляющих проводимостей в ветвях
Слайд 42Признаки резонанса токов
Токи ветвей равны IPC=IPL и находятся в противофазе.
Токи ветвей
превышают полный ток цепи, который имеет минимальное значение.
и совпадают по фазе, φ= 0
и совпадают по фазе, φ= 0
Слайд 43Частотные характеристики цепей синусоидального тока
R – активное сопротивление не зависит от
частоты
XL,XC – реактивные сопротивления зависят от частоты
XL,XC – реактивные сопротивления зависят от частоты
На графиках показаны зависимости тока, полного комплексного сопротивления и угла сдвига фаз от частоты
Слайд 44Коэффициент мощности в цепях синусоидального тока
Увеличение напряжения U приведет к увеличению
изоляции проводов, увеличение тока I приведет к увеличению площади сечения проводов.
Слайд 45Повышение коэффициента мощности в цепях синусоидального тока
IR совпадает с U следовательно
φ=0, cosφ=1 и Р=Рмах
Имеется возможность:
использовать для неразветвленного участка провода меньшей площади сечения
использовать источник меньшей мощности
подключать к источнику дополнительную нагрузку
Имеется возможность:
использовать для неразветвленного участка провода меньшей площади сечения
использовать источник меньшей мощности
подключать к источнику дополнительную нагрузку
