- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электронные лекции по разделам оптики, квантовой механики, атомной и ядерной физики презентация
Содержание
- 1. Электронные лекции по разделам оптики, квантовой механики, атомной и ядерной физики
- 2. Лекция 2. Волновая оптика. Дифракция и дисперсия
- 3. 2.1. Дифракция света. Принцип Гюйгенса. Принцип
- 4. Принцип Гюйгенса: каждая точка фронта волны является
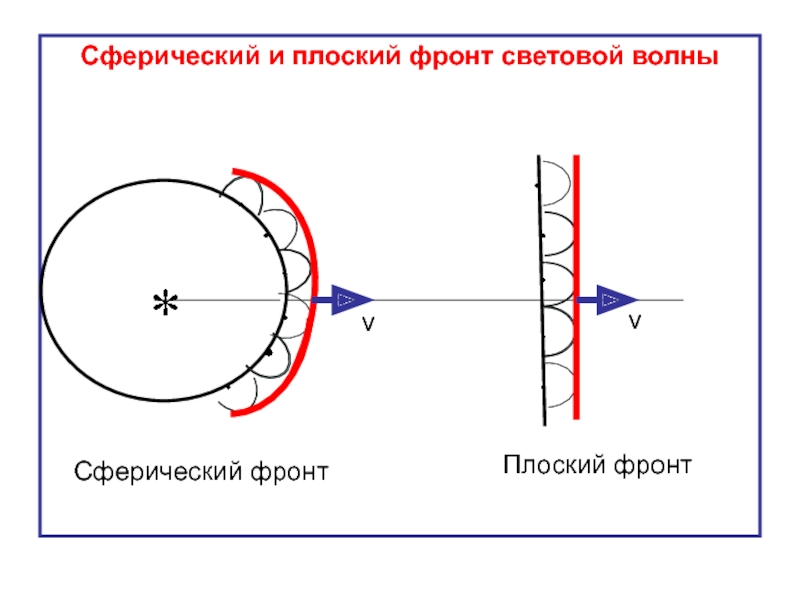
- 5. Сферический и плоский фронт световой волны
- 6. Дифракция вторичных когерентных волн может проявиться на
- 7. Принцип Гюйгенса не позволял рассчитать интенсивность света
- 8. Принцип Гюйгенса – Френеля
- 9. 4. Колебание от элемента dS пройдёт расстояние
- 10. Множители
- 11. 2.2. Метод зон Френеля Полностью открытый фронт
- 12. Сферический фронт волны (красная линия)
- 13. Введём расстояния: а – от источника света
- 14. Площадь всех зон одинакова; не зависит от
- 15. Амплитуды волн, приходящих в точку экрана Р
- 16. Результирующая амплитуда в точке Р определяется следующей
- 17. В итоге суммирования: При достаточно
- 18. При полностью открытом фронте световой волны (
- 19. Рассмотрим два случая. Непрозрачный экран закрывает
- 20. Условия наблюдения максимумов и минимумов света
- 21. 2.3. Дифракция Френеля на круглом отверстии и
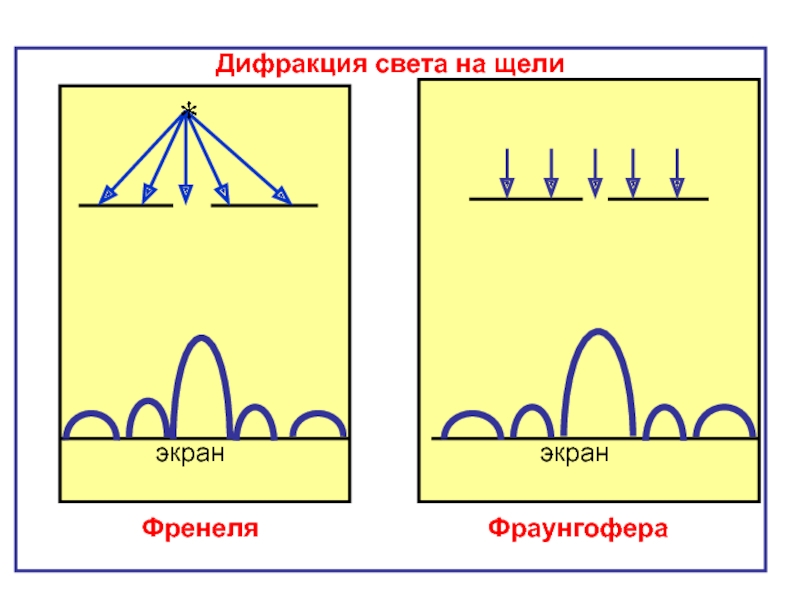
- 22. Дифракция света на щели
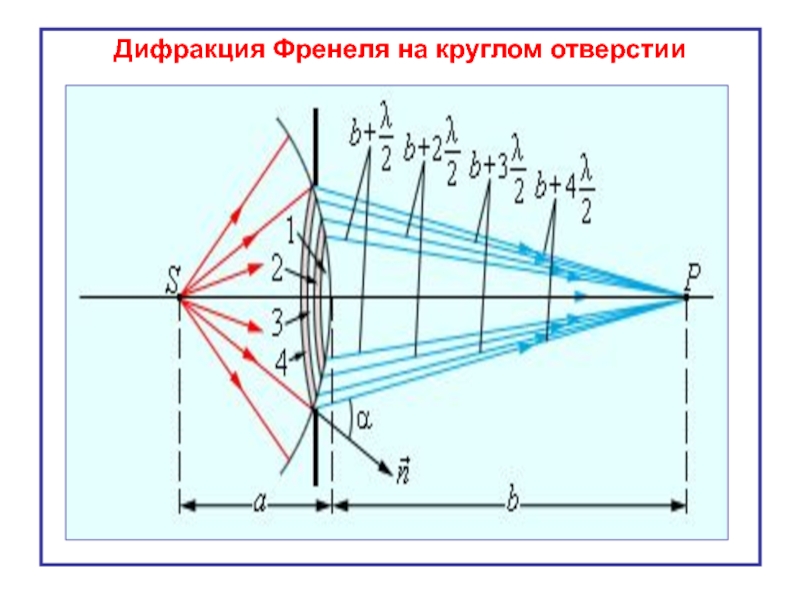
- 23. Дифракция Френеля на круглом отверстии
- 24. Пусть на непрозрачный экран с круглым отверстием
- 25. Результирующая амплитуда в точке Р экрана наблюдения,
- 26. Если число зон чётное, то в центре
- 27. Анализ дифракционной картины 1. При переходе
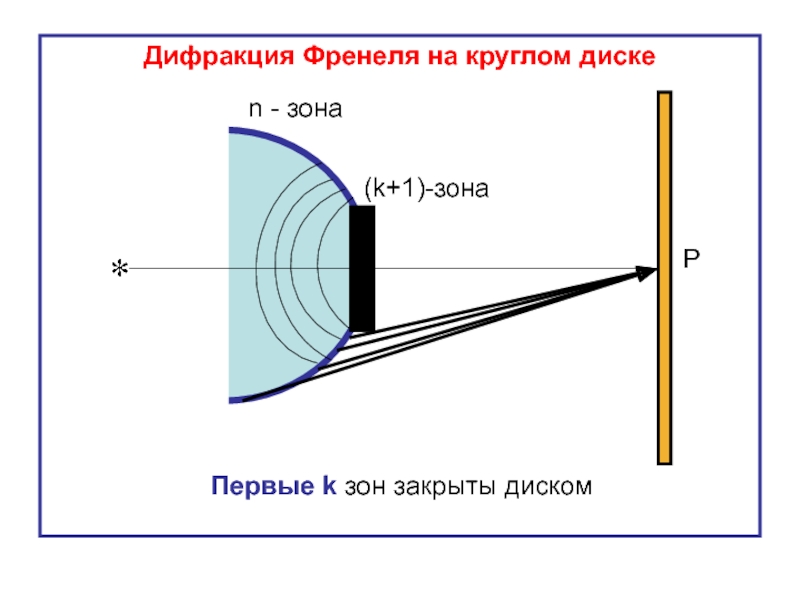
- 28. Дифракция Френеля на круглом диске
- 29. При небольших размерах диска (
- 30. Вывод: результирующая амплитуда равна половине амплитуды волны,
- 31. 2.4. Дифракция Фраунгофера на щели Рассмотрим падение
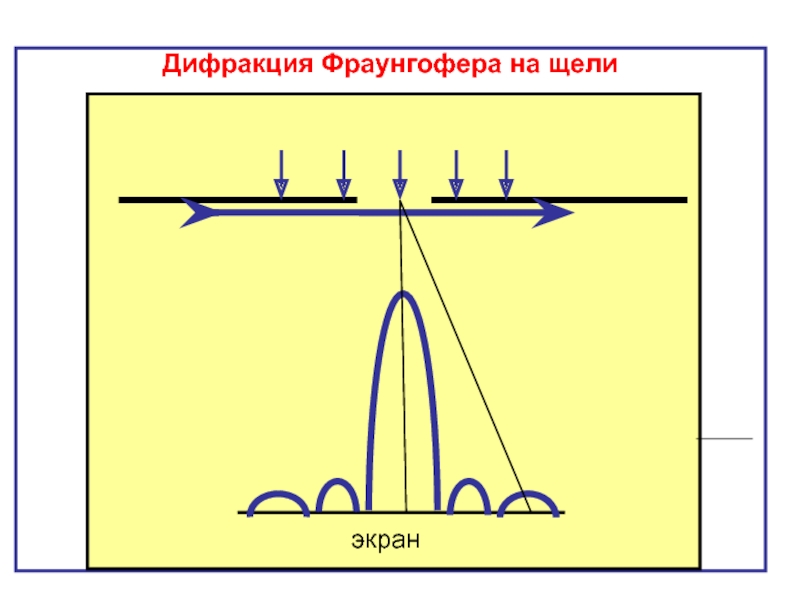
- 32. Дифракция Фраунгофера на щели
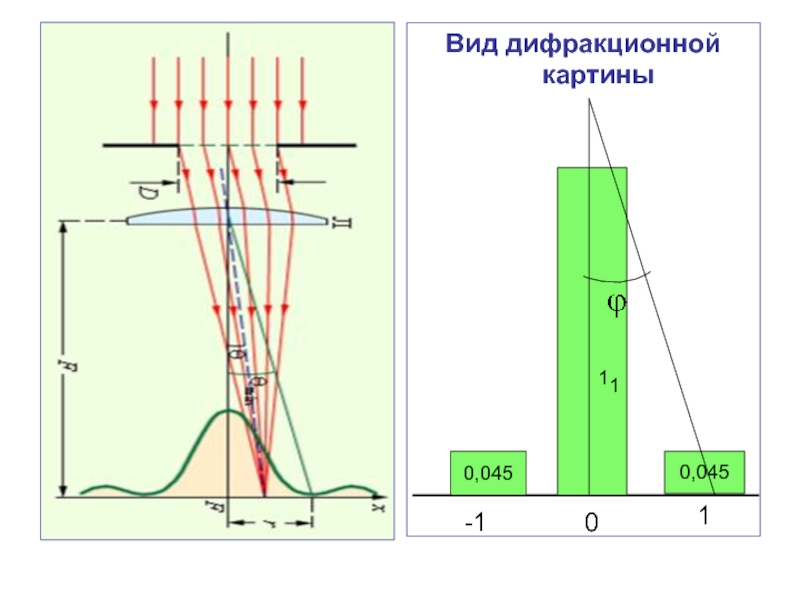
- 33. Вид дифракционной картины 0,045 0,045 0 1 -1 1 1
- 34. Все лучи, идущие под углом
- 36. Количество зон Френеля, уложившихся на ширине щели:
- 37. Условие наблюдения максимумов света:
- 38. Количество максимумов в дифракционной картине определяется как
- 39. Чёткая дифракционная картина от щели наблюдается, если
- 40. 2.5. Дифракция Фраунгофера на дифракционной решётке Дифракционную
- 41. Дифракционная решетка прибор для наблюдения дифракционного спектра
- 42. Решётка имеет N щелей на длине L.
- 43. Схема наблюдения дифракционной картины -1 -2 0 1 2
- 44. Дифракционная картина представляет собой чередование очень интенсивных
- 45. Максимальный наблюдаемый порядок главного максимума определяется условием
- 46. Условие наблюдения любых минимумов: k
- 47. Распределение интенсивности при дифракции света на решетках
- 48. При увеличении числа щелей N в дифракционной
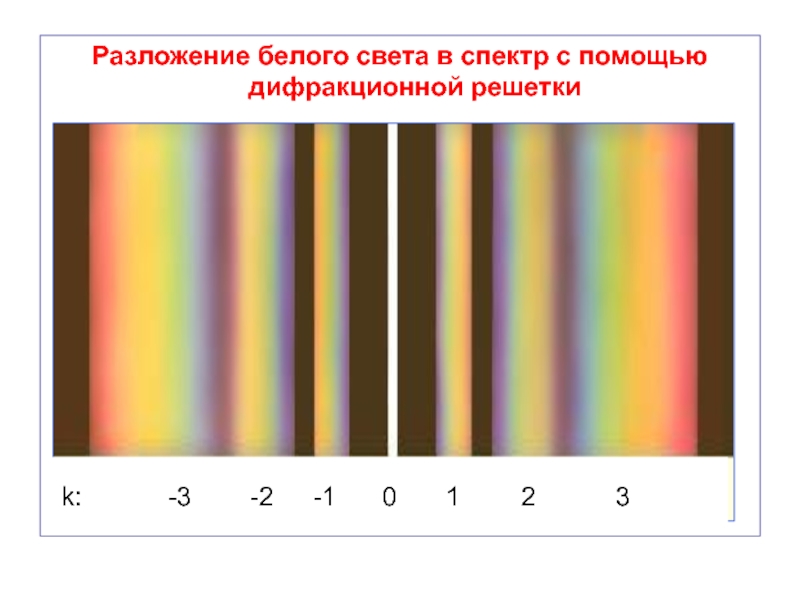
- 49. Разложение белого света в спектр с помощью
- 50. Дифракционный спектр 1. В каждом порядке
- 51. 4. В каждом порядке ближе к нулевому
- 52. Разрешающая сила оптических приборов - важная
- 53. Изображение любой светящейся точки, наблюдение которой ведётся
- 54. Точечный источник отображается в виде центрального светлого
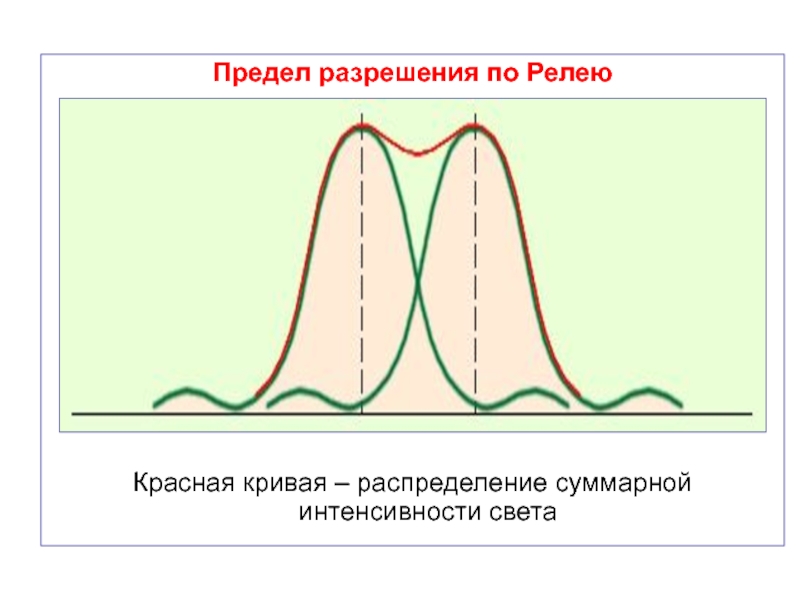
- 55. Предел разрешения по Релею
- 56. 2.6. Дифракция рентгеновских лучей Кристаллы для рентгеновских
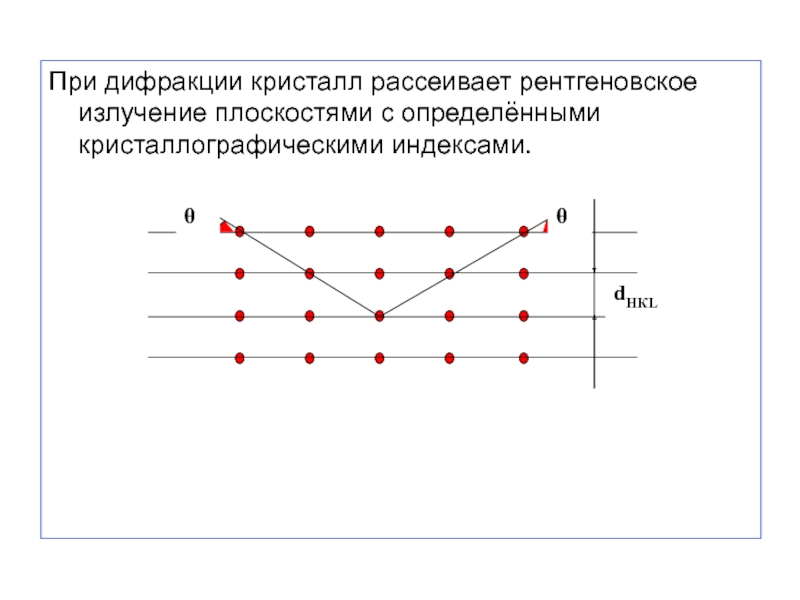
- 57. При дифракции кристалл рассеивает рентгеновское излучение плоскостями с определёнными кристаллографическими индексами.
- 58. В направлении угла дифракции θ будет
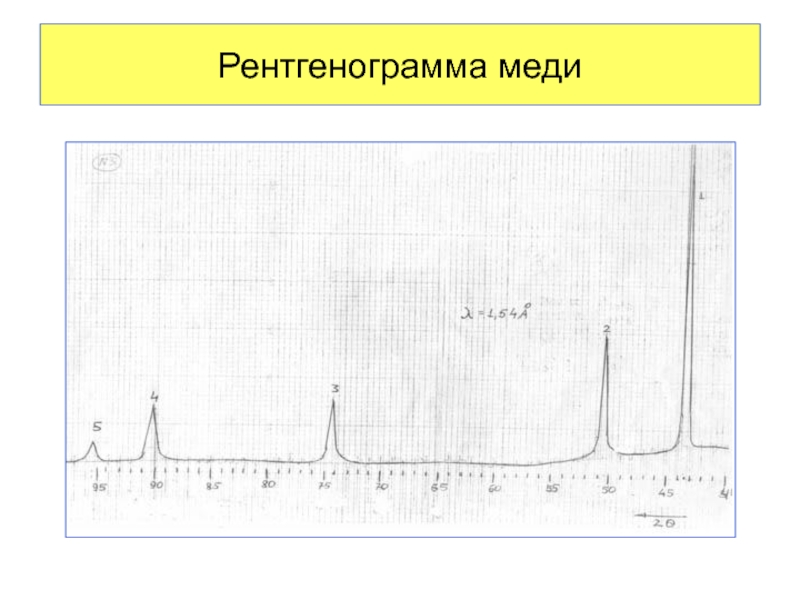
- 59. Рентгенограмма меди
- 60. 2.7. Дисперсия света. Спектры поглощения Дисперсия волн
- 61. Призматический спектр: 1. Является сплошным (переход цветов
- 62. Нормальная дисперсия - явление, при котором показатель
- 63. В области нормальной дисперсии D < 0.
- 64. Аномальная дисперсия: показатель преломления увеличивается при увеличении
- 65. Дисперсией обладают все среды, кроме вакуума.
- 66. Когда ω >> ω0 или ω
- 67. Абсолютный показатель преломления среды n зависит от
- 68. Зависимость показателя преломления от частоты света описывается
- 69. График зависимости показателя преломления от частоты света
- 70. Поглощением света называется явление уменьшения энергии световой волны,
- 71. Прохождение света через вещество График закона Бугера L IO I I IO L
- 72. Коэффициент поглощения (k): обратно пропорционален той толщине
- 73. Линейчатый спектр поглощения
- 74. Твёрдые тела (прозрачные диэлектрики) дают широкие полосы
- 75. Коэффициент поглощения для металлов имеет большие значения
Слайд 1Омский государственный технический университет
Кафедра физики
Калистратова Л.Ф.
Электронные лекции по разделам оптики,
9 лекций
(18 аудиторных часов)
Слайд 2Лекция 2. Волновая оптика.
Дифракция и дисперсия света
План лекции
2.1. Дифракция света. Принцип
2.2. Метод зон Френеля.
2.3. Дифракция Френеля на круглом отверстии и диске.
2.4. Дифракция Фраунгофера на щели.
2.5. Дифракция Фраунгофера на дифракционной решётке.
2.6. Дифракция рентгеновских лучей.
2.7. Дисперсия света.
2.8. Поглощение света. Спектры поглощения.
Слайд 32.1. Дифракция света.
Принцип Гюйгенса. Принцип Гюйгенса-Френеля
Дифракция света - явление перераспределения
В основу волновой теории света положен принцип Гюйгенса, который позволял представить способ получения большого числа когерентных световых волн.
Слайд 4Принцип Гюйгенса: каждая точка фронта волны является источником вторичных когерентных сферических
Огибающая этих волн дает положение волнового фронта в последующий момент времени.
Если предыдущий фронт волны был сферическим, то и последующий фронт волны будет сферическим.
Если предыдущий фронт волны был плоским, то и последующий фронт волны будет плоским.
Слайд 6Дифракция вторичных когерентных волн может проявиться на резких неоднородностях среды и
к огибанию световыми волнами препятствий;
захождению света в область геометрической тени.
Условия наблюдения дифракции света:
Если эти размеры препятствия соизмеримы с длиной волны света, то дифракция наблюдается в непосредственной близости от препятствия.
2. Если длина волны света много меньше размеров препятствия, то дифракция становится заметной на расстояниях, значительно превышающих размеры самого препятствия.
Слайд 7Принцип Гюйгенса не позволял рассчитать интенсивность света в дифракционной картине.
Принцип Гюйгенса
Действие источника света заменяется действием волновой поверхности (фронта волны).
Каждый элемент dS этой светящейся поверхности является источником вторичных когерентных сферических волн.
2. Элементы поверхности dS гармонически колеблются с амплитудой ЕО и частотой ω согласно уравнению:
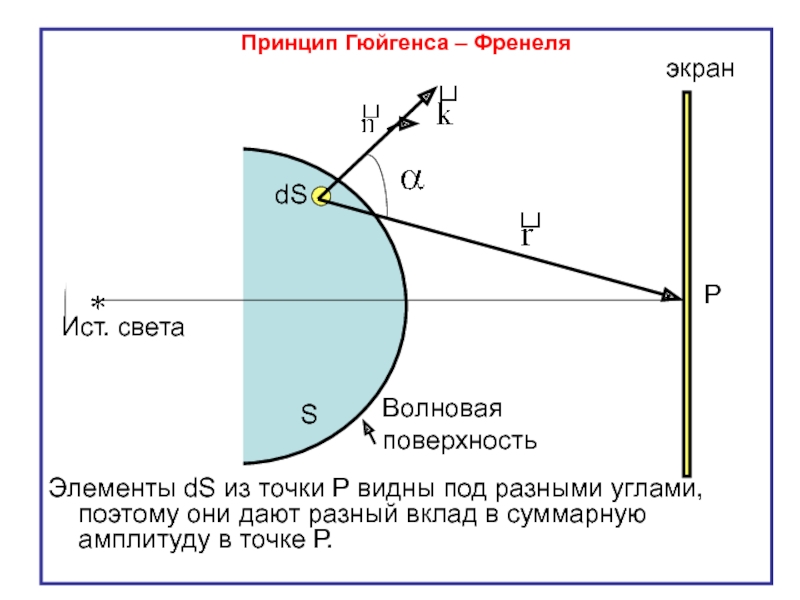
Слайд 8Принцип Гюйгенса – Френеля
Элементы dS из точки Р видны под разными
Р
dS
S
Ист. света
экран
Волновая
поверхность
Слайд 94. Колебание от элемента dS пройдёт расстояние r до точки наблюдения
5. Волны, пришедшие от всех элементов dS волновой поверхности, накладываясь, дают на экране дифракционную картину в виде чередования максимумов и минимумов.
6. Результирующая амплитуда световой волны в точке Р запишется через интегральное суммирование амплитуд волн, пришедших от всех элементов поверхности S.
Слайд 10
Множители зависят от
При В = 1
В = 0
Поскольку вычисление интеграла – сложная задача, Френель предложил геометрический метод сложения амплитуд, названный методом зон Френеля.
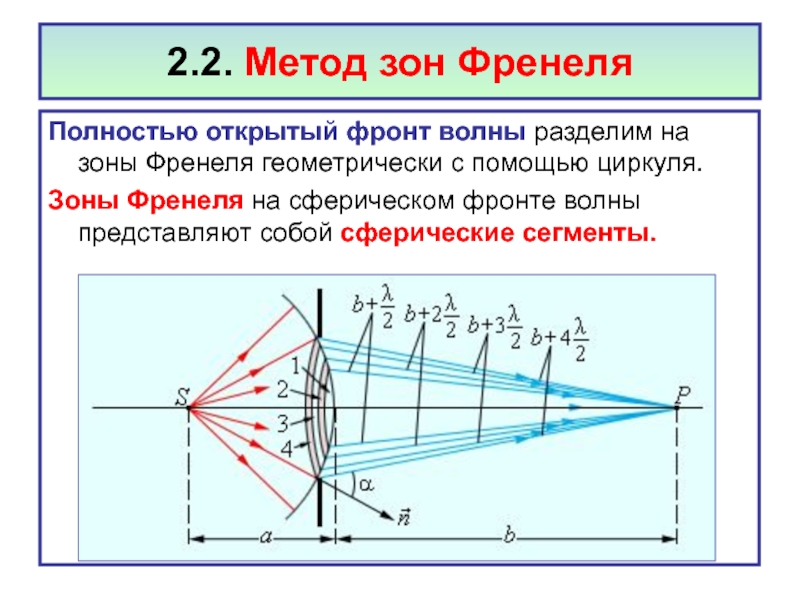
Слайд 112.2. Метод зон Френеля
Полностью открытый фронт волны разделим на зоны Френеля
Зоны Френеля на сферическом фронте волны представляют собой сферические сегменты.
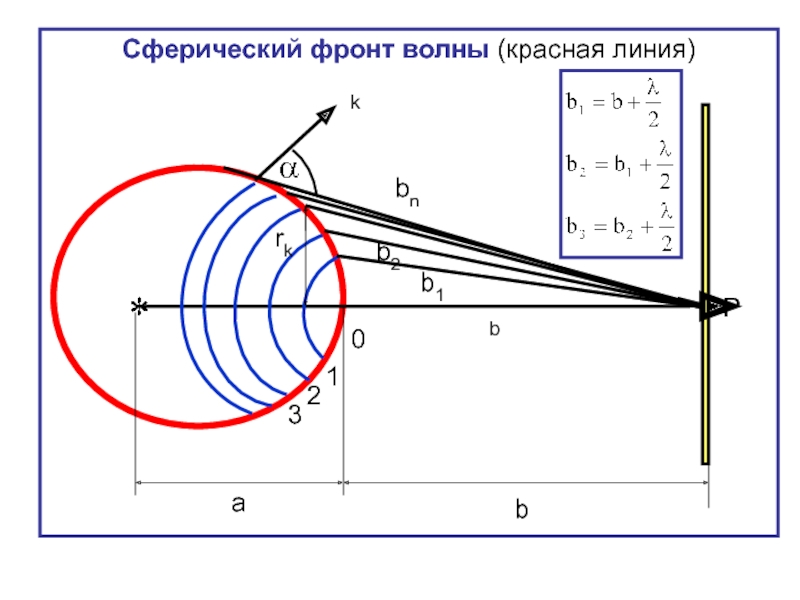
Слайд 13Введём расстояния:
а – от источника света до сферического фронта волны;
b -
На волновой поверхности проведём
ряд окружностей радиусами:
Нумеруем зоны: 0,1, 2, 3,…,k,…n .
Общее число зон (N)– велико,
практически стремится
к бесконечности.
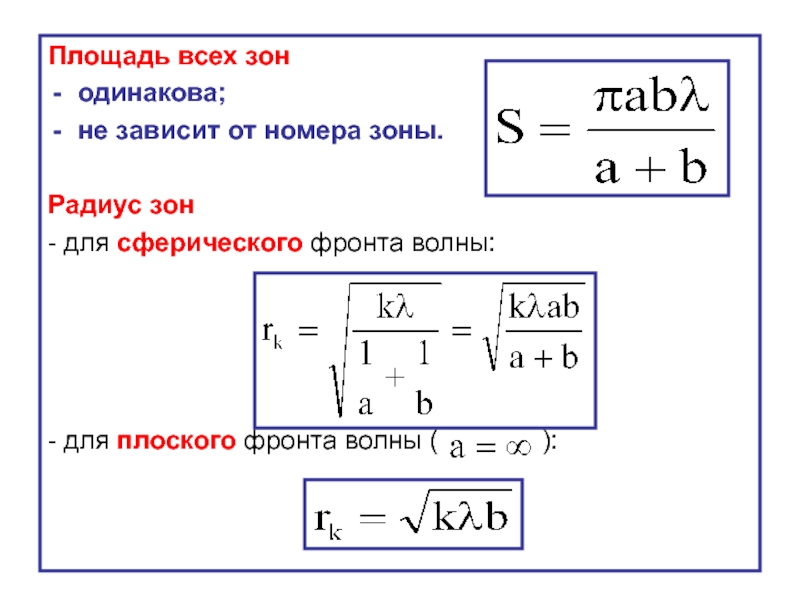
Слайд 14Площадь всех зон
одинакова;
не зависит от номера зоны.
Радиус зон
- для сферического
- для плоского фронта волны ( ):
Слайд 15Амплитуды волн, приходящих в точку экрана Р от каждой последующей зоны,
ЕО, Е1, Е2, Е3, …, Еn
Расстояния, проходимые волнами от краёв соседних зон, отличаются на , поэтому в точку Р волны приходят в противофазах: происходит чередование знака амплитуд.
Каждая последующая амплитуда меньше предыдущей за счёт увеличения проходимого волной расстояния r и увеличения угла наклона зоны
:
Слайд 16Результирующая амплитуда в точке Р определяется следующей суммой:
Выражение представляет собой монотонно
Каждая амплитуда такого ряда определяется как среднее арифметическое двух соседних амплитуд этого ряда:
Представим теперь знакопеременный ряд в виде суммы соответствующих «скобок». Все «скобки» равны нулю.
Слайд 17В итоге суммирования:
При достаточно большом числе зон амплитуда последней зоны Еn=0.
Окончательно
Вывод: результирующая амплитуда от полностью открытого фронта волны равна половине амплитуды волны, пришедшей от центральной зоны Френеля.
Слайд 18При полностью открытом фронте световой волны ( т.е. если нет преград)
-
в однородной среде от точечного источника к точке наблюдения свет распространяется прямолинейно.
Если принять , то число зон N = 107, радиус центральной зоны равен 0,1 мм.
Слайд 19Рассмотрим два случая.
Непрозрачный экран закрывает все зоны, кроме центральной.
Результирующая амплитуда
2. Непрозрачный экран закрывает все нечётные зоны (зонная пластинка).
Получим ещё большее усиление интенсивности света на экране.
Слайд 20Условия наблюдения
максимумов и минимумов света при дифракции
Максимумы света наблюдаются в
Минимумы света наблюдаются, если свет в точку наблюдения приходит от чётного числа зон Френеля:
N – число зон Френеля,
k - целое число:
Слайд 212.3. Дифракция Френеля на круглом отверстии и диске
Различают два вида дифракции:
дифракцию
дифракцию Фраунгофера (дифракцию в параллельных лучах).
Схема получения дифракционной картины для указанных типов дифракции показана на рисунках.
Слайд 24Пусть на непрозрачный экран с круглым отверстием падает расходящийся пучок лучей
Разобьём подошедший к отверстию сферический фронт волны на зоны Френеля.
В отверстии уложатся только несколько первых k зон Френеля.
Остальные зоны от k+1 до n-ой зоны закрыты непроницаемым экраном.
Слайд 25Результирующая амплитуда в точке Р экрана наблюдения, согласно правилу сложения амплитуд,
При небольшом числе k амплитуды соизмеримы между собой:
Освещённость в центре дифракционной картины на экране зависит от числа зон Френеля, которые уместились в круглом отверстии.
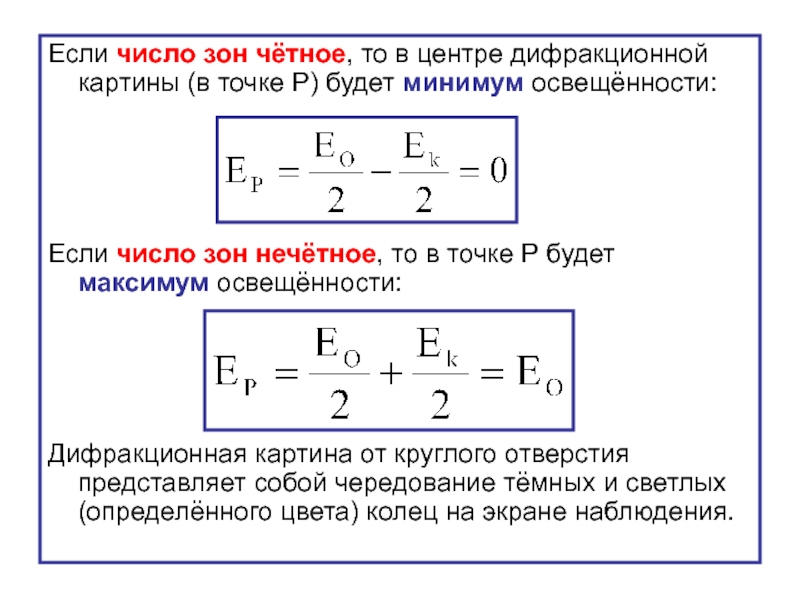
Слайд 26Если число зон чётное, то в центре дифракционной картины (в точке
Если число зон нечётное, то в точке Р будет максимум освещённости:
Дифракционная картина от круглого отверстия представляет собой чередование тёмных и светлых (определённого цвета) колец на экране наблюдения.
Слайд 27Анализ дифракционной картины
1. При переходе от центра дифракционной картины к периферии
2. При изменении расстояния между источником света и экраном будет меняться число зон, укладывающихся в отверстие.
3. Центральное пятно при этом будет менять свою освещённость от максимального до нулевого значения.
4. Дифракционная картина будет наблюдаться только в случае соизмеримости размера отверстия с длиной волны света:
Слайд 29
При небольших размерах диска (
Суммирование амплитуд начнётся с первой открытой (k+1) - ой зоны Френеля до последней n -ой зоны:
Результирующая амплитуда в центральной точке экрана не зависит от того, сколько зон закроет непрозрачный диск.
Слайд 30Вывод: результирующая амплитуда равна половине амплитуды волны, пришедшей от первой открытой
В центре дифракционной картины всегда будет наблюдаться максимум света.
Дифракция света на диске будет слабо выражена при больших размерах диска и когда экран находится слишком близко к диску.
Слайд 312.4. Дифракция Фраунгофера на щели
Рассмотрим падение плоской монохроматической световой волны на
Свет проходит сквозь щель и линзу, помещённую параллельно непрозрачному экрану.
Дифракционную картину наблюдают на экране, расположенном в фокальной плоскости линзы.
Из всей совокупности вторичных когерентных волн плоского фронта волны, расположенного в щели, выделим лучи, идущие под углом к главной оптической оси линзы.
Слайд 34Все лучи, идущие под углом , линзой
Дано:
а – ширина щели;
- угол дифракции;
- длина волны света;
k – порядок максимума.
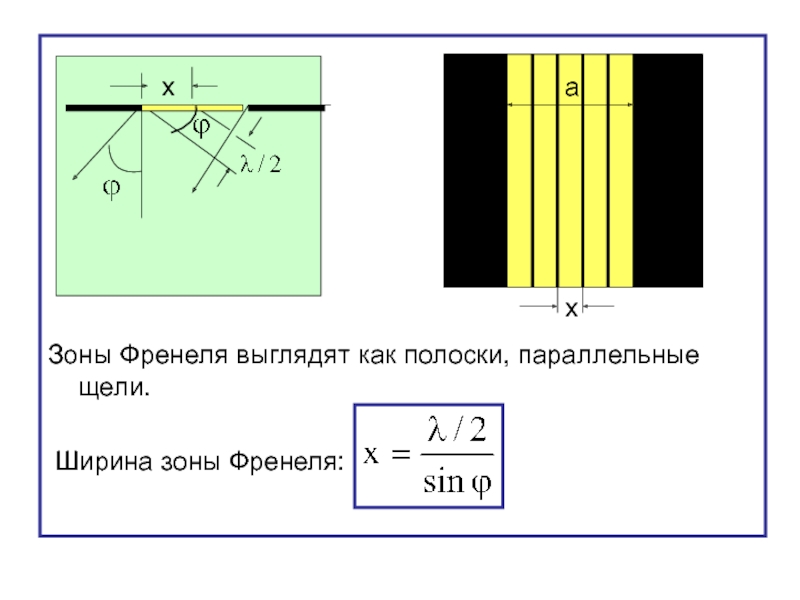
Подошедший к щели плоский фронт волны разбиваем на зоны Френеля.
Количество зон Френеля, укладывающихся на ширине щели, зависит от угла дифракции .
Слайд 36Количество зон Френеля, уложившихся на ширине щели:
В точке Р экрана будут
максимумы, если в эту точку свет приходит от нечётного число зон Френеля:
минимумы – если свет приходит от чётного число зон Френеля:
Слайд 37Условие наблюдения максимумов света:
Условие наблюдения минимумов света:
В дифракционной картине максимумы располагаются
Цвет всех максимумов одинаков.
Максимальный порядок максимума определяется при значении :
Слайд 38Количество максимумов в дифракционной картине определяется как
С увеличением порядка максимума интенсивность снижается, а угловая ширина максимума увеличивается.
IO : I1 : I2 = 1: 0,045 : 0,016
При уменьшении ширины щели число максимумов уменьшается, а их угловая ширина увеличивается.
Слайд 39Чёткая дифракционная картина от щели наблюдается, если ширина щели в несколько
При получается почти равномерная освещённость экрана: слабо освещённый широкий центральный максимум.
При количество максимумов становится настолько большим, что они не будут различаться невооружённым глазом, получится достаточно резкое изображение щели.
Слайд 402.5. Дифракция Фраунгофера на дифракционной решётке
Дифракционную картину на экране можно получить,
Дифракционная решётка – совокупность регулярно расположенных одинаковых дифракционных элементов (препятствий, отверстий, щелей - штрихов).
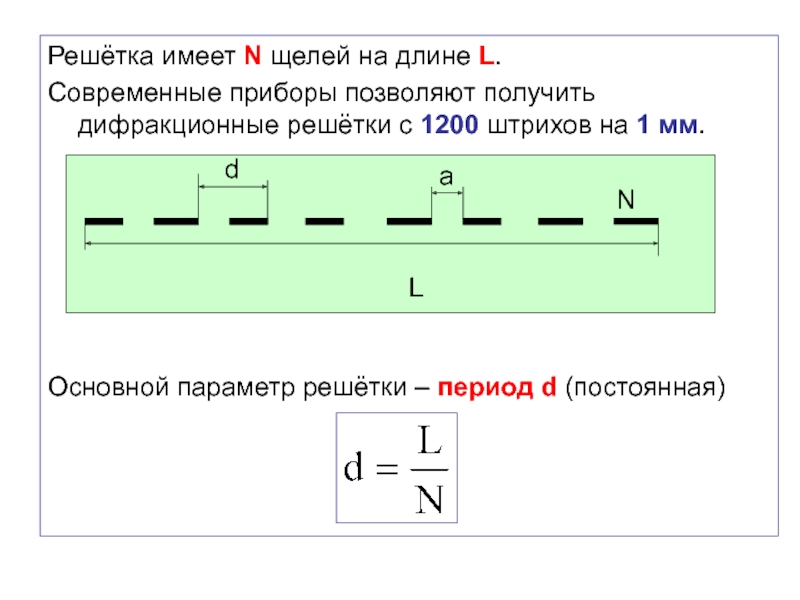
Слайд 42Решётка имеет N щелей на длине L.
Современные приборы позволяют получить дифракционные
Основной параметр решётки – период d (постоянная)
L
N
d
a
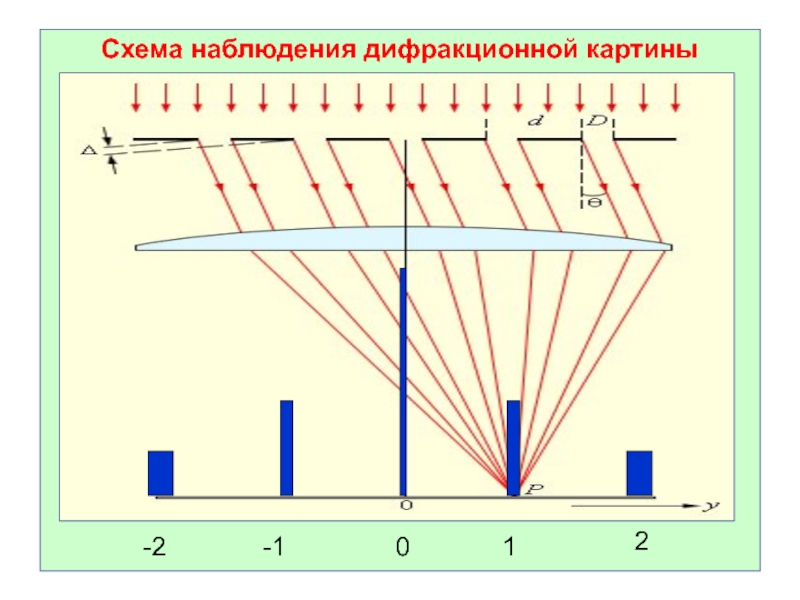
Слайд 44Дифракционная картина представляет собой чередование очень интенсивных и узких дифракционных максимумов
Главные максимумы наблюдаются в направлениях:
- порядок главных максимумов.
Всего наблюдается
главных максимумов:
Слайд 45Максимальный наблюдаемый порядок главного максимума определяется условием
В минимумах интенсивность сосредоточена
Условие наблюдения
дополнительных максимумов:
- принимает все целые числа, кроме 0, N, 2N, 3N,..
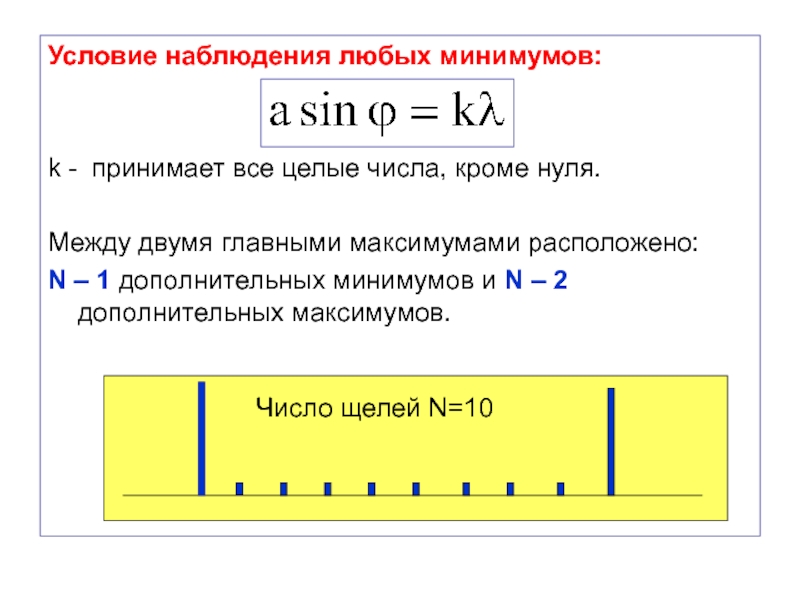
Слайд 46Условие наблюдения любых минимумов:
k - принимает все целые числа, кроме нуля.
Между
N – 1 дополнительных минимумов и N – 2 дополнительных максимумов.
Число щелей N=10
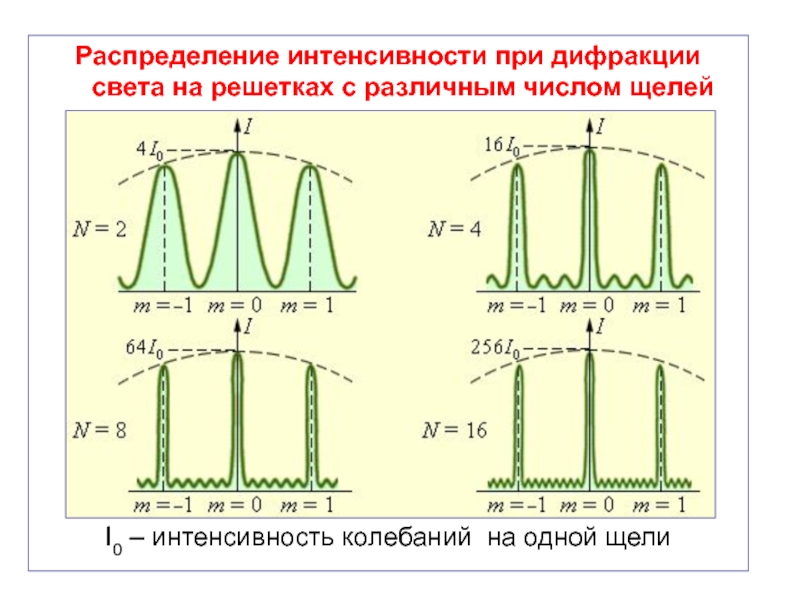
Слайд 47Распределение интенсивности при дифракции света на решетках с различным числом щелей
I0
Слайд 48При увеличении числа щелей N в дифракционной решётке по сравнению с
увеличивается интенсивность главных максимумов;
уменьшается ширина главных максимумов.
Если дифракционная решётка освещается белым светом, то на экране наблюдается дифракционный спектр нескольких порядков.
Слайд 50Дифракционный спектр
1. В каждом порядке наблюдаются:
те же цветные максимумы;
меньшей интенсивности;
занимаемые больший
2. Центральный максимум имеет белый цвет, так как все волны с разными длинами при k = 0 придут в одну точку экрана и, складываясь, снова образуют белый свет.
3. Спектр – линейчатый.
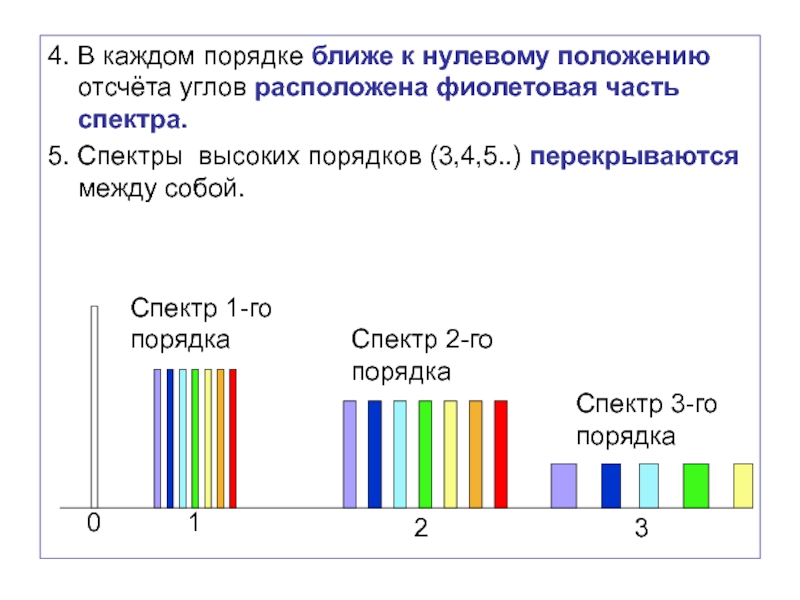
Слайд 514. В каждом порядке ближе к нулевому положению отсчёта углов расположена
5. Спектры высоких порядков (3,4,5..) перекрываются между собой.
0
1
2
3
Спектр 1-го
порядка
Спектр 2-го
порядка
Спектр 3-го
порядка
Слайд 52Разрешающая сила оптических приборов
- важная характеристика дифракционной решётки и других оптических
характеризует способность решётки разделять максимумы двух близких длин волн света и
Разрешающая сила решётки зависит:
от числа щелей N;
порядка спектра k.
Слайд 53Изображение любой светящейся точки, наблюдение которой ведётся оптической системой (например, телескопом)
В центральное пятно попадает приблизительно 85 % энергии света.
Слайд 54Точечный источник отображается в виде центрального светлого пятна, окружённого чередующимися тёмными
Английский физик Дж. Релей в конце XIX в. предложил
изображение двух близких источников света (например, двух звёзд) считать различимыми, если центральный максимум дифракционной картины от одного источника совпадает с первым минимумом дифракционной картины от другого источника.
При выполнении критерия Релея интенсивность провала между максимумами составляет 80 % в максимуме, что является достаточным для разрешения линий и .
Слайд 562.6. Дифракция рентгеновских лучей
Кристаллы для рентгеновских лучей являются естественными пространственными дифракционными
Межатомные расстояния в кристаллах соизмеримы с длиной волны рентгеновского излучения.
Дифракцию рентгеновских лучей на кристаллах можно представить как их рассеяние плоскостями кристаллической решётки.
Слайд 57При дифракции кристалл рассеивает рентгеновское излучение плоскостями с определёнными кристаллографическими индексами.
Слайд 58 В направлении угла дифракции θ будет наблюдаться максимум интенсивности лучей,
d - межплоскостное расстояние,
λ - длина волны характеристического рентгеновского излучения,
k - порядок максимума: k = ±1, ±2…
Слайд 602.7. Дисперсия света. Спектры поглощения
Дисперсия волн - явление зависимости частоты волны
Дисперсия света – явление зависимости показателя преломления вещества от частоты света (или длины волны).
Явление дисперсии света легко наблюдать при пропускании света через призму.
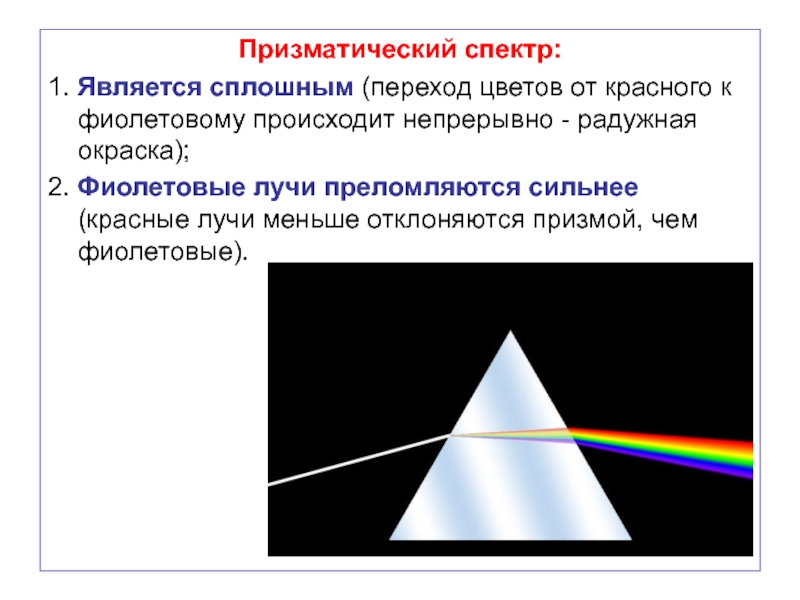
Слайд 61Призматический спектр:
1. Является сплошным (переход цветов от красного к фиолетовому происходит
2. Фиолетовые лучи преломляются сильнее (красные лучи меньше отклоняются призмой, чем фиолетовые).
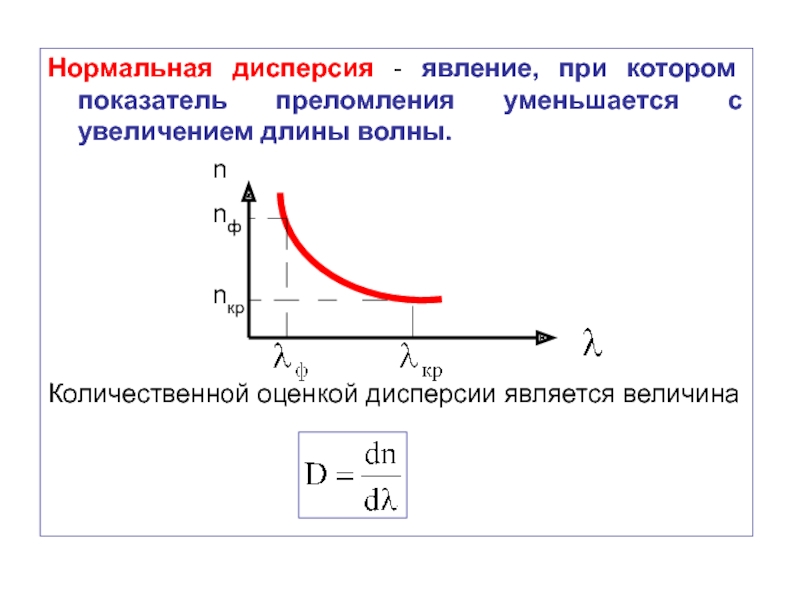
Слайд 62Нормальная дисперсия - явление, при котором показатель преломления уменьшается с увеличением
Количественной оценкой дисперсии является величина
n
nф
nкр
Слайд 63В области нормальной дисперсии D < 0.
Нормальная дисперсия наблюдается для видимых
Первое объяснение дисперсии основано на электромагнитной природе света и описывает область нормальной дисперсии формулой Коши:
,
где А,В,С – константы вещества.
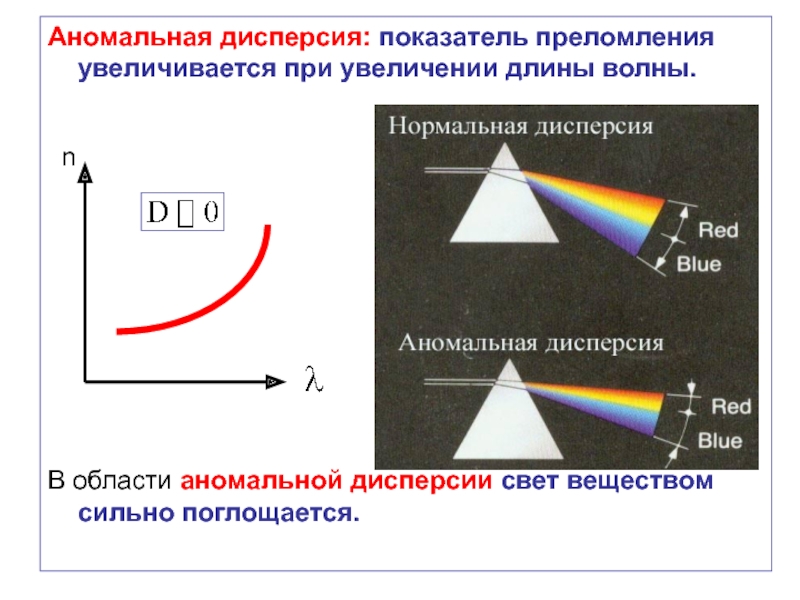
Слайд 64Аномальная дисперсия: показатель преломления увеличивается при увеличении длины волны.
В области аномальной
n
Слайд 65Дисперсией обладают все среды, кроме вакуума.
В вакууме скорость распространения световых
Электронная теория дисперсии
основана на электромагнитной природе света и явлении резонанса.
Падающая на вещество световая волна частоты ω вызывает вынужденные колебания валентных (слабо связанных с ядром) электронов, имеющих собственную частоту колебаний ω0 .
Слайд 66Когда ω >> ω0 или ω
При совпадении частоты (ω = ω0), наступает резонанс.
Амплитуда колебаний электронов резко возрастает (аномальная дисперсия), что сопровождается сильным поглощением света.
Слайд 67Абсолютный показатель преломления среды n зависит от диэлектрических и магнитных свойств
Диэлектрическая восприимчивость зависит от частоты света.
Слайд 68Зависимость показателя преломления от частоты света описывается формулой:
Суммирование ведётся по количеству
N – число атомов в единице объёма вещества.
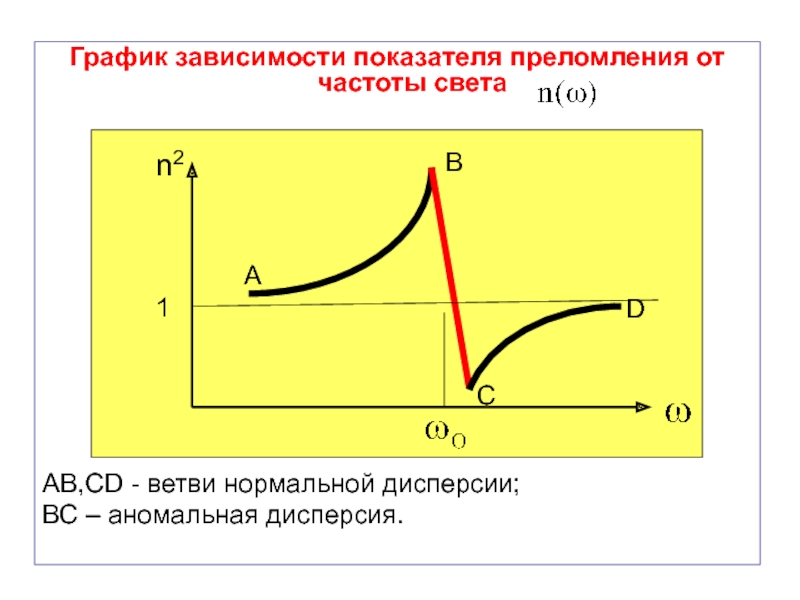
Слайд 69График зависимости показателя преломления от частоты света
AB,CD - ветви нормальной дисперсии;
ВС – аномальная дисперсия.
1
n2
A
B
C
D
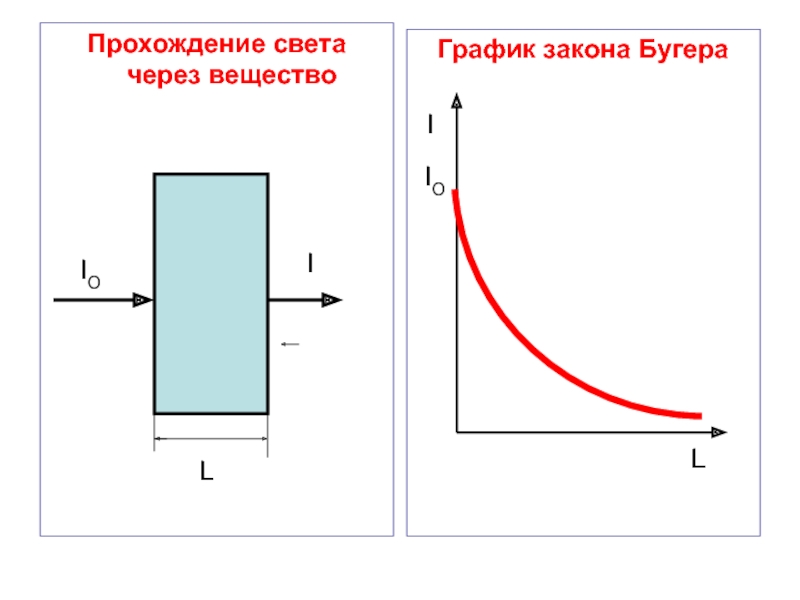
Слайд 70Поглощением света называется явление уменьшения энергии световой волны, проходящей через вещество.
Пусть свет
Закон поглощения света
Закон Бугера:
интенсивность света уменьшается по экспоненциальному закону.
2.8. Поглощение света. Спектры поглощения
Слайд 72Коэффициент поглощения (k):
обратно пропорционален той толщине вещества, которая уменьшает интенсивность света
чем больше k, тем сильнее свет поглощается веществом;
зависит от длины волны света (спектры поглощения).
Спектры поглощения могут быть:
- линейчатыми;
полосатыми;
практически сплошными (в таких спектрах наблюдаются узкие полосы пропускания).
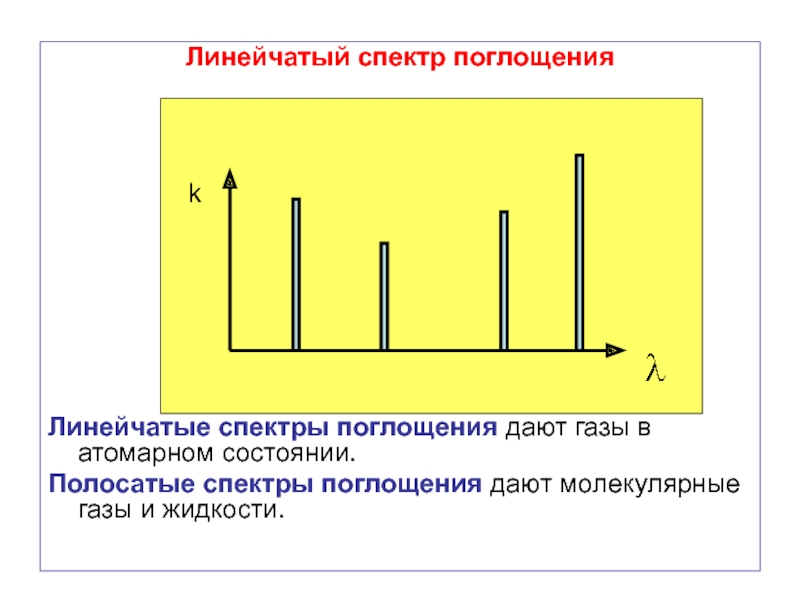
Слайд 73Линейчатый спектр поглощения
Линейчатые спектры поглощения дают газы в атомарном состоянии.
Полосатые спектры
k
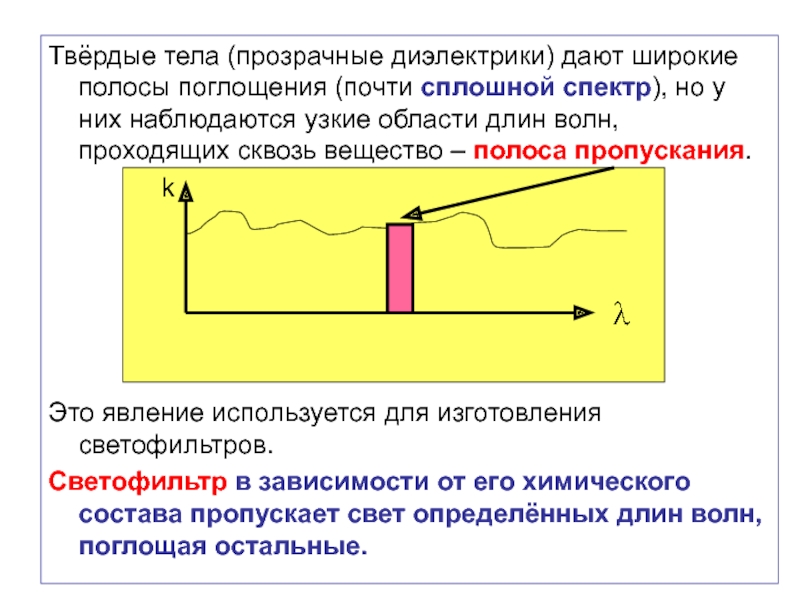
Слайд 74Твёрдые тела (прозрачные диэлектрики) дают широкие полосы поглощения (почти сплошной спектр),
Это явление используется для изготовления светофильтров.
Светофильтр в зависимости от его химического состава пропускает свет определённых длин волн, поглощая остальные.
k
Слайд 75Коэффициент поглощения для металлов имеет большие значения (примерно 103-104 см-1).
Коэффициент поглощения
Одноатомные газы и пары металлов (т.е. вещества, в которых атомы расположены на значительных расстояниях друг от друга и их можно считать изолированными) обладают близким к нулю коэффициентом поглощения.