- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнение состояния реального газа Ван-Дер-Ваальса. (Лекция 11) презентация
Содержание
- 1. Уравнение состояния реального газа Ван-Дер-Ваальса. (Лекция 11)
- 2. На рис. изображены экспериментальные кривые зависимости произведения
- 3. МКТ идеального газа не объясняет этой закономерности.
- 4. Атомы и молекулы вещества – сложные системы
- 5. Поправка на собственный объем молекул (учет сил
- 6. В расчете на одну
- 7. Можно получить, что внутренне давление обратно пропорционально
- 8. Теоретические и экспериментальные изотермы реального газа. Фазовые
- 9. Семейство теоретических изотерм Ван-дер-Ваальса для некоторых значений
- 10. При повышении температуры максимум и минимум на
- 11. ВС – конденсация пара. Как видно
- 12. Если через крайние точки горизонтальных участков изотерм
- 13. Критическое состояние вещества – состояние, при котором
- 14. Внутренняя энергия реального газа
- 15. Работа консервативных сил притяжения
- 16. Таким образом, внутренняя энергия одного моля газа
- 17. При расширении (V)2 > (V)1, следовательно, Т2
Слайд 1УРАВНЕНИЕ СОСТОЯНИЯ РЕАЛЬНОГО ГАЗА ВАН-ДЕР-ВААЛЬСА
Разреженные реальные газы при не слишком низких
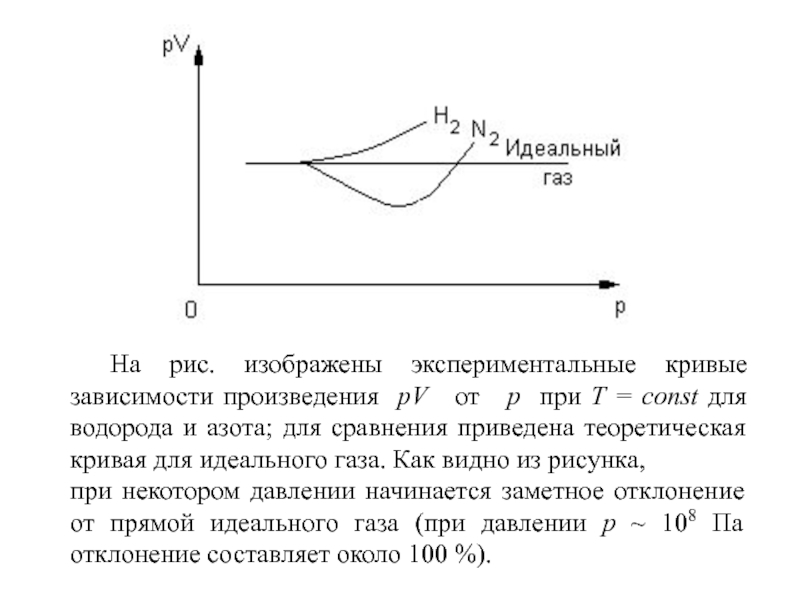
Слайд 2 На рис. изображены экспериментальные кривые зависимости произведения pV от
при некотором давлении начинается заметное отклонение от прямой идеального газа (при давлении р ~ 108 Па отклонение составляет около 100 %).
Слайд 3 МКТ идеального газа не объясняет этой закономерности. Самым простым из них
Слайд 4 Атомы и молекулы вещества – сложные системы движущихся заряженных частиц, между
Рассмотрим поправки на силы отталкивания и притяжения.
Слайд 5 Поправка на собственный объем молекул (учет сил отталкивания). В уравнении состояния
Vμ представляет собой объем сосуда, занятого газом, и в то же врем объем пространства, доступный для движения молекул, т.к. молекулы идеального газа не имеют собственного объема. В реальном газе объем, доступный для движения молекул, меньше объема Vμ на величину недоступного объема b.
Слайд 6
В расчете на одну молекулу, недоступным оказывается объем, равный учетверенному объему
b = 4Vмол NА ,
где NA – число Авогадро.
Слайд 7 Можно получить, что внутренне давление обратно пропорционально квадрату молярного объема:
Таким
Сделав замену
Слайд 8Теоретические и экспериментальные изотермы реального газа.
Фазовые превращения
Рассмотрим теоретические изотермы реального газа,
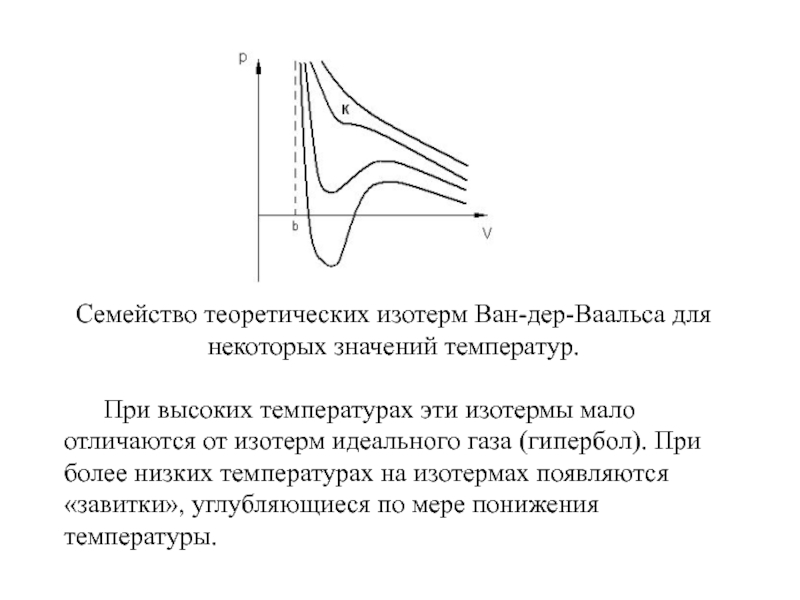
Слайд 9Семейство теоретических изотерм Ван-дер-Ваальса для некоторых значений температур.
При высоких температурах
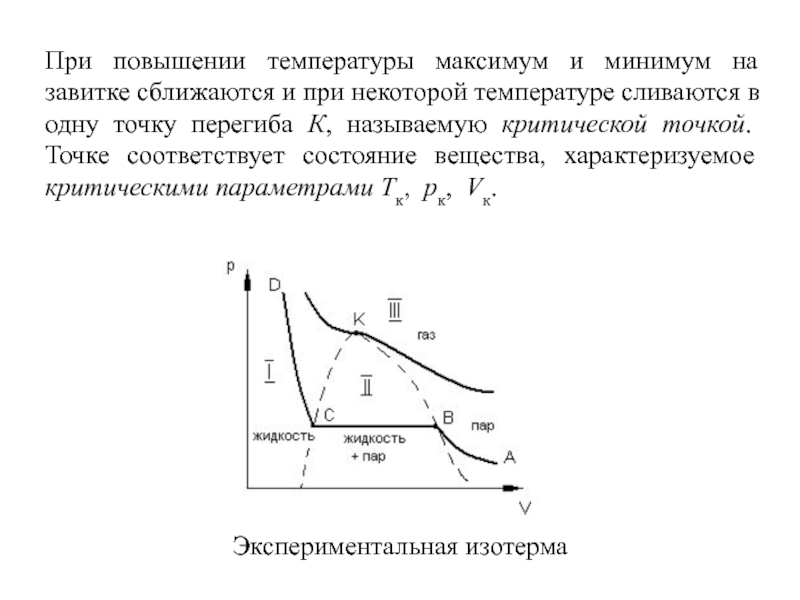
Слайд 10При повышении температуры максимум и минимум на завитке сближаются и при
Экспериментальная изотерма
Слайд 11
ВС – конденсация пара. Как видно из диаграммы, конденсация происходит при
СD – жидкое состояние. Давление при сжатии резко возрастает. Участок СD снова удовлетворительно согласуется с уравнением Ван-дер-Ваальса.
Экспериментальная изотерма состоит из трех участков. АВ – переход пара из ненасыщенного состояния в насыщенное. Этот участок изотермы удовлетворительно согласуется с уравнением Ван-дер-Ваальса.
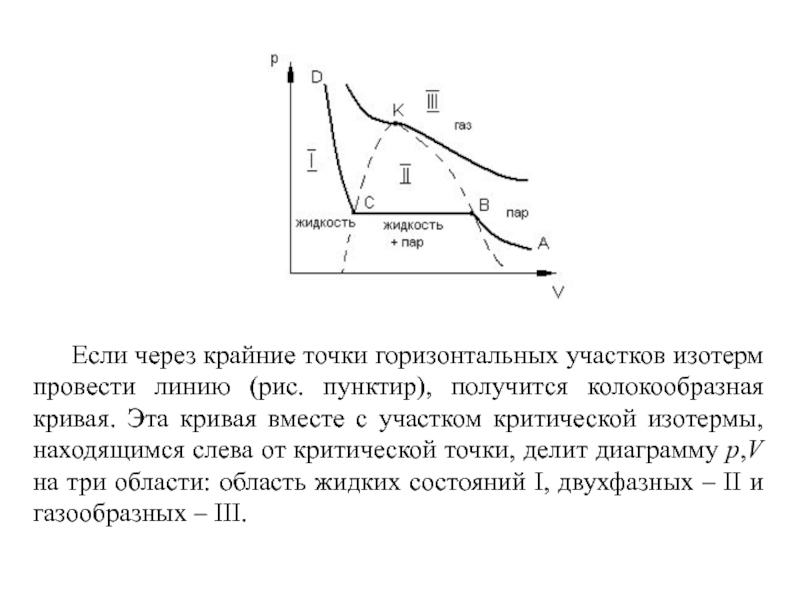
Слайд 12Если через крайние точки горизонтальных участков изотерм провести линию (рис. пунктир),
Слайд 13 Критическое состояние вещества – состояние, при котором исчезает различие между жидкостью
Соблюдая должные предосторожности, можно получить состояния, соответствующие начальным участкам завитка на теоретической изотерме Ван-дер-Ваальса. Эти состояния соответствуют малоустойчивым метастабильным состояниям – пересыщенному пару и перегретой жидкости.
Слайд 14Внутренняя энергия реального газа
Внутренняя энергия реального газа складывается из кинетической энергии
где (Cμ)V – молярная теплоемкость при постоянном объеме
При расширении реального газа силы притяжения совершают отрицательную работу:
где рi – внутреннее давление.
Кинетическая энергия молекул
Слайд 15
Работа консервативных сил притяжения равна убыли потенциальной энергии газа
Проинтегрируем выражение
Константу
Тогда
Слайд 16Таким образом, внутренняя энергия одного моля газа равна
При расширении реального газа
Приравняв правые части этих выражений:
Слайд 17 При расширении (V)2 > (V)1, следовательно, Т2 < Т1 , т.е.
При адиабатическом дросселировании температура газа может и понижаться, и повышаться, и оставаться равной нулю. Дросселирование – стационарный переход газа от одного давления р1 к другому р2 через препятствие, создающее большое трение. Роль такого препятствия может играть пористая перегородка.
Изменение температуры реального газа при его адиабатическом дросселировании называется эффектом Джоуля-Томсона.