- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электрическое поле в вакууме. (Тема 13) презентация
Содержание
- 1. Электрическое поле в вакууме. (Тема 13)
- 2. Тема 13. Электрическое поле в вакууме 1.
- 3. Электростатика – это раздел физики, в котором
- 4. 4. Фундаментальный закон сохранения электричес-кого заряда (выполняется
- 5. 1 учебный вопрос: Закон Кулона. Закон
- 6. Взаимодействия зарядов передаются с помощью особого материального
- 7. Напряженность – есть сила, действующая на единичный точечный заряд.
- 8. Напряженность электрического поля точечного заряда (2)
- 9. Принцип суперпозиции полей Напряженность поля, создаваемая в
- 10. Напряженность поля непрерывно распределенного заряда Характеристики
- 11. Графическое изображение электрических полей. Силовые линии. Силовые
- 12. Примеры электрических полей
- 14. 2 учебный вопрос: Работа по перемещению заряда
- 15. Работа по перемещению заряда не
- 16. При движении заряда по замкнутой траектории
- 17. 3 учебный вопрос: Потенциальная энергия и
- 18. Отношение потенциальной энергии W к заряду q0
- 19. Принцип суперпозиции Если поле
- 20. Разность потенциалов Работа, совершаемая электрическими силами
- 21. Графическое изображение электрических полей. Эквипотенциальные поверхности.
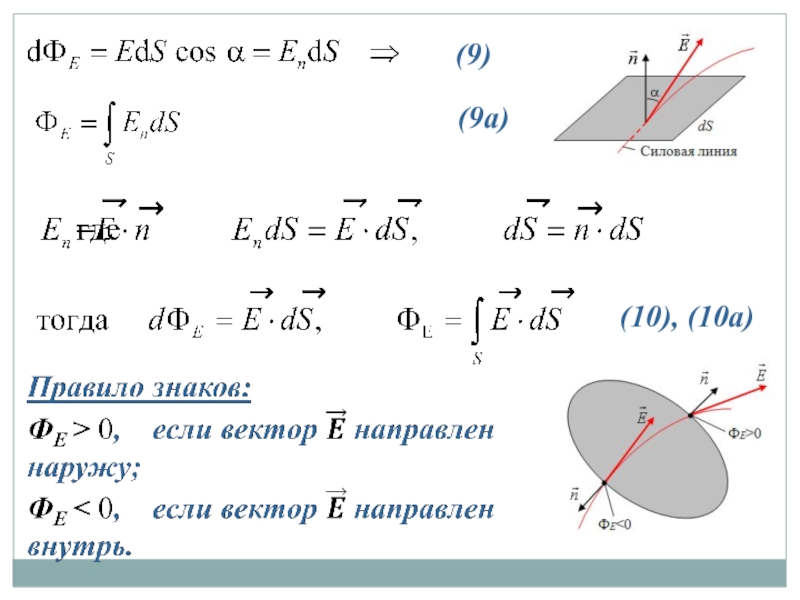
- 22. 4 учебный вопрос: Связь между напряженностью и
- 23. Матанализ: - производная функции по направлению - вектор нормали к поверхности ϕ =const
- 24. Пример Однородное поле плоского конденсатора (Е=const) Единицы измерения (8)
- 25. 5 учебный вопрос: Поток вектора напряженности электростатического поля. Теорема Гаусса.
- 26. (10), (10а) (9) (9а)
- 27. Поток ФЕ, создаваемый единичным положительным зарядом площадь сферы для точечного заряда (11)
- 28. Для произвольного распределения зарядов поток вектора ФЕ
- 29. - теорема Гаусса Поток вектора напряженности
- 30. 6 учебный вопрос: Применение теоремы Гаусса к
- 31. С учетом Вне сферы
- 32. Объёмно заряженный шар Объемная плотность заряда
- 33. Бесконечная однородно заряженная плоскость
Слайд 1Раздел 4: Электростатика и постоянный электрический ток
Тема13. Электрическое поле в вакууме
Тема14.
Тема15. Диэлектрики в электрическом поле
Тема16. Постоянный электрический ток
Слайд 2Тема 13. Электрическое поле в вакууме
1. Закон Кулона. Электростатическое поле.
2. Работа
3. Потенциальная энергия и потенциал.
4. Связь между напряженностью и потенциалом.
5. Поток вектора напряженности электростатического поля. Теорема Гаусса.
6. Применение теоремы Гаусса к расчету электростатических полей.
Слайд 3Электростатика – это раздел физики, в котором изучается взаимодействие и свойства
Электрические заряды
1. Электрический заряд – носитель электромагнит-ного взаимодействия.
2. Электрический заряд может быть двух типов: положительный (при трении кожи о стекло) и отрицательный (при трении меха с эбонитом).
2. Носителями электрического заряда являются заряженные элементарные частицы с элементарным зарядом e=1.6⋅10-19 Кл : протон, электрон.
Слайд 44. Фундаментальный закон сохранения электричес-кого заряда (выполняется в любых процессах рождения
В любой электрически изолированной системе алгебраическая сумма зарядов не изменяется.
5. Электрический заряд является релятивистcки инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.
Слайд 51 учебный вопрос: Закон Кулона.
Закон Кулона – закон о взаимодействии
Сила взаимодействия F двух неподвижных точечных зарядов q1 и q2 в вакууме направлена вдоль линии, соединяющей оба заряда, прямо пропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния между ними:
где k – коэффициент пропорциональности, зависящий от выбора единиц измерения. В системе СИ
электрическая постоянная
(1)
Слайд 6Взаимодействия зарядов передаются с помощью особого материального посредника, называемого электрическим полем.
Действие электрического поля на помещенный в него заряд является основным его свойством.
Электрическое поле, созданное неподвижными зарядами, называется электростатическим (ЭСП).
Характеристики ЭСП в вакууме:
напряженность (векторная) и потенциал (скалярная)
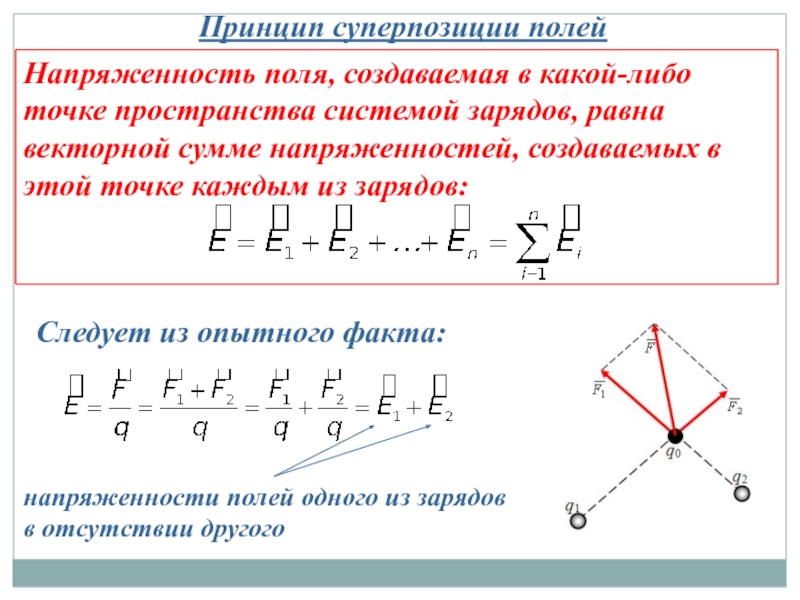
Слайд 9Принцип суперпозиции полей
Напряженность поля, создаваемая в какой-либо точке пространства системой зарядов,
Следует из опытного факта:
напряженности полей одного из зарядов в отсутствии другого
Слайд 10Напряженность поля непрерывно распределенного заряда
Характеристики распределенных зарядов
− линейная плотность зарядов;
− поверхностная
− объемная плотность зарядов.
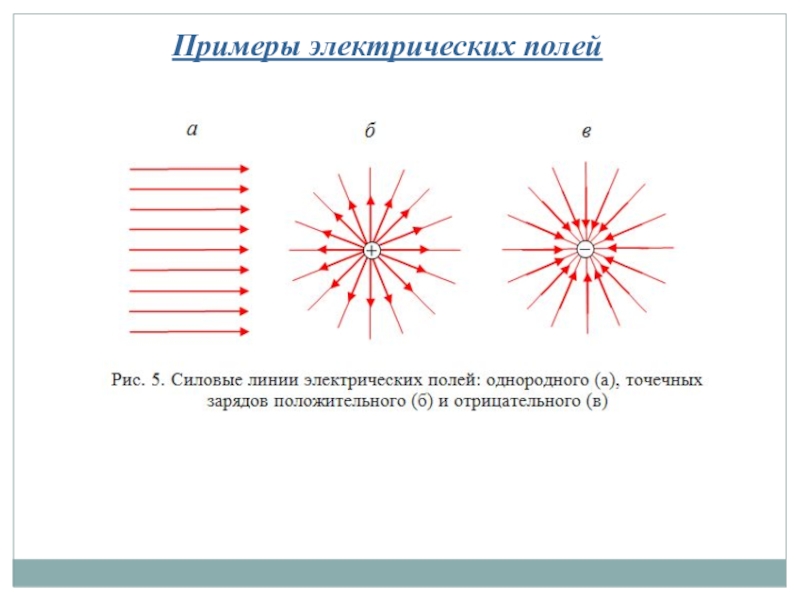
Слайд 11Графическое изображение электрических полей. Силовые линии.
Силовые линии – это непрерывные линии,
Свойства силовых линий:
- всегда начинаются на «+» зарядах и заканчиваются на «-» ;
- густота силовых линий пропорциональна напряженности электрического поля;
- не пересекаются.
Слайд 142 учебный вопрос: Работа по перемещению заряда в электростатическом поле.
Определим
Работа по перемещению заряда q0 из точки 1 в точку 2:
Слайд 15
Работа по перемещению заряда не зависит от формы траектории и пройденного
Такое поле называется потенциальным, а кулоновская сила – консервативной.
(3)
Слайд 16При движении заряда по замкнутой траектории
(r1 = r2) работа равна
Если циркуляция поля равна нулю, то поле является потенциальным.
Слайд 17
3 учебный вопрос: Потенциальная энергия и потенциал.
Потенциальная энергия заряда q0, находящегося
(4)
Слайд 18Отношение потенциальной энергии W к заряду q0 не зависит от заряда
Потенциалом называется скалярная величина, характеризующая энергию, которой обладает заряд, помещенный в данную точку поля, и численно равная потенциальной энергии единичного положительного заряда в этой точке поля:
(5)
(5а)
Потенциал поля точечного заряда:
Слайд 19Принцип суперпозиции
Если поле создается системой зарядов q1, q2, …, qn,
Потенциал поля, создаваемого системой точечных зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности
Слайд 20
Разность потенциалов
Работа, совершаемая электрическими силами при перемещении заряда между двумя точками
Свойства:
(6)
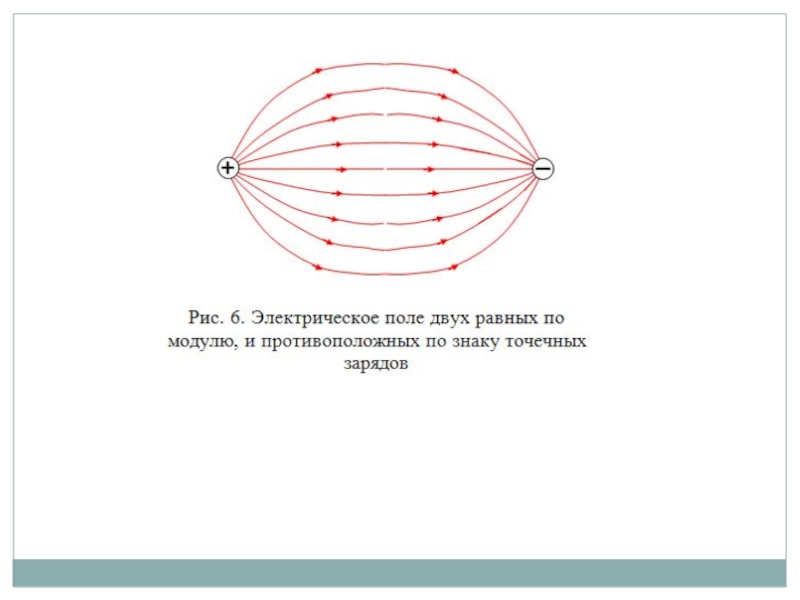
Слайд 21Графическое изображение электрических полей.
Эквипотенциальные поверхности.
Эквипотенциальной поверхностью называется геометрическое место точек
Свойства эквипотенциальных поверхностей
- работа, совершаемая по перемещению заряда вдоль этой поверхности, равна нулю;
- кулоновская сила направлена перпендикулярно этой поверхности;
- эквипотенциальные поверхности не пересекаются;
- густота линий равного потенциала пропорциональна градиенту напряженности электрического поля.
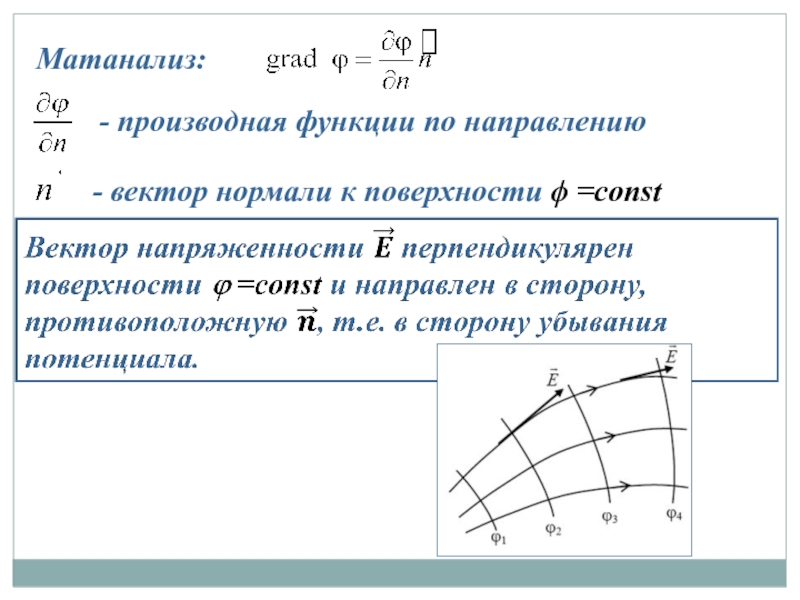
Слайд 224 учебный вопрос: Связь между напряженностью и потенциалом.
Работа на бесконечно малом
(7)
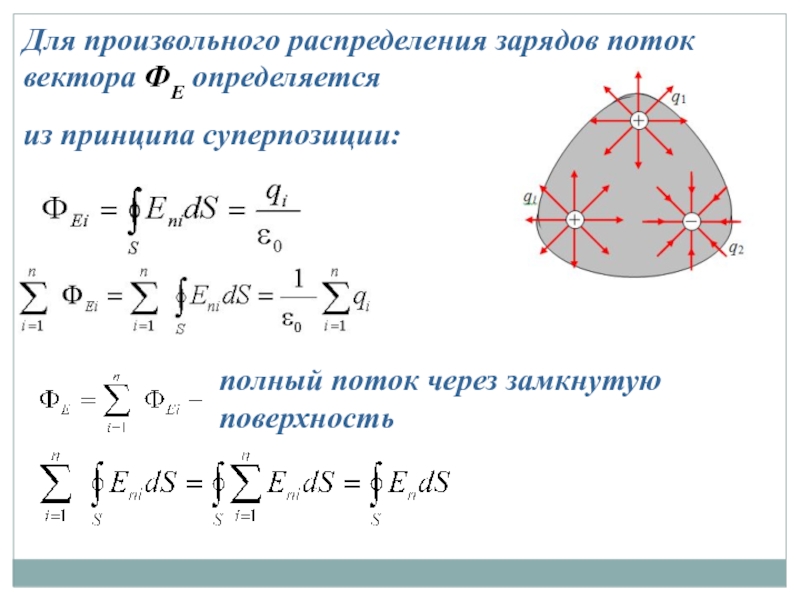
Слайд 28Для произвольного распределения зарядов поток вектора ФЕ определяется
из принципа суперпозиции:
полный поток
Слайд 29- теорема Гаусса
Поток вектора напряженности ЭСП через произвольную замкнутую поверхность
Для непрерывно распределенного заряда с объемной плотностью ρ = dQ/dV , Кл/м3:
(12)
(13)
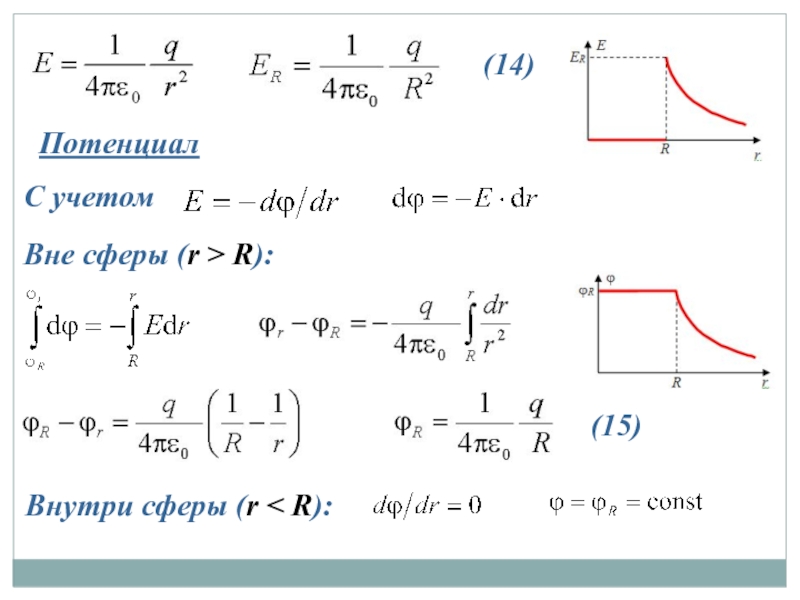
Слайд 306 учебный вопрос: Применение теоремы Гаусса к расчету электростатических полей.
Внутри сферы
Е=0, поле внутри сферы отсутствует
Вне сферы (r > R):
Поверхностно заряженная сфера