- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электрические однофазные цепи синусоидального тока презентация
Содержание
- 1. Электрические однофазные цепи синусоидального тока
- 3. +Eмах -Eмах е ωt T е1
- 4. u = Umахsin(ωt + ψu),,
- 5. Действующим значением синусоидального тока называют такое значение
- 6. За среднее значение синусоидального тока принимают такое
- 7. Синусоидальная величина изображается вращающимся вектором на комплексной
- 8. Переход из одной формы записи в другую
- 9. Закон Oма для участка цепи:
- 12. Мощность цепи с R-элементом: p
- 13. Напряжение u = Umахsinωt еL
- 14. Векторная и временная диаграмма цепи с идеальной индуктивностью
- 15. P = ui = Umахsinωt *
- 16. Комплексное сопротивление цепи с
- 17. . По II ЗК Кирхгофа:
- 18. Векторная и временная диаграмма цепи с конденсатором
- 19. Р = ui = Uмахsinωt * I
- 20. u = UmахRsinωt + UmахLsin(ωt +
- 21. = IR + I jXL −
- 22. Z = U/I R = UR/I X
- 23. Резонанс – это явление в электрической цепи,
- 24. Параллельное соединение R, L, C U
- 25. ,
- 26. I = YU = ϕ =
- 27. Y1 = 1/Z1 =
- 28. Резонанс токов нашел
- 29. В электрической цепи, к которой приложено
- 30. Расчет электрической цепи комплексным методом ведут
- 31. 1. Катушка индуктивности L = 0,032 Гн
Слайд 1Электрические однофазные цепи синусоидального тока
Электрические однофазные цепи синусоидального тока
В
ток синусоидальной формы. Это обусловлено рядом преимуществ:
– генераторы синусоидального тока значительно дешевле в производстве, чем
генераторы постоянного тока;
– переменный ток легко преобразуется в постоянный;
– трансформация и передача электрической энергии переменным током экономичнее
чем постоянным;
– двигатели переменного тока имеют простую конструкцию, высокую надежность и
невысокую стоимость.
В настоящее время переменный ток применяется в промышленном приводе и в
электроосвещении, в сельском хозяйстве и на транспорте, в технике связи и в быту.
Производство электрической энергии также осуществляется на переменном токе.
Огромную роль в деле внедрения переменного тока сыграли русские ученые
П.Н.Яблочков и М.О.Доливо-Добровольский
Слайд 2
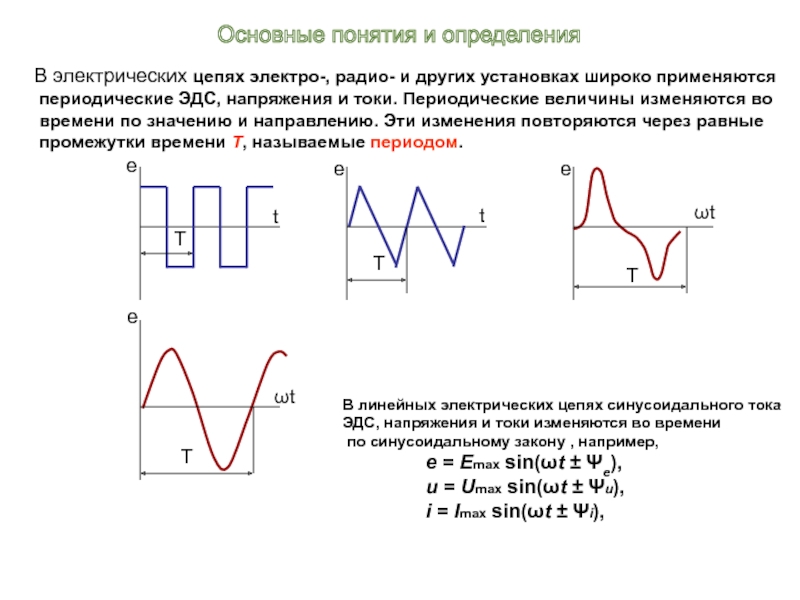
В электрических цепях электро-, радио- и других установках широко применяются
периодические ЭДС, напряжения и токи. Периодические величины изменяются во
времени по значению и направлению. Эти изменения повторяются через равные
промежутки времени Т, называемые периодом.
е
t
T
е
t
T
е
ωt
T
ωt
е
В линейных электрических цепях синусоидального тока
ЭДС, напряжения и токи изменяются во времени
по синусоидальному закону , например,
e = Emах sin(ωt ± Ψe),
u = Umах sin(ωt ± Ψu),
i = Imах sin(ωt ± Ψi),
Основные понятия и определения
T
Слайд 3
+Eмах
-Eмах
е
ωt
T
е1
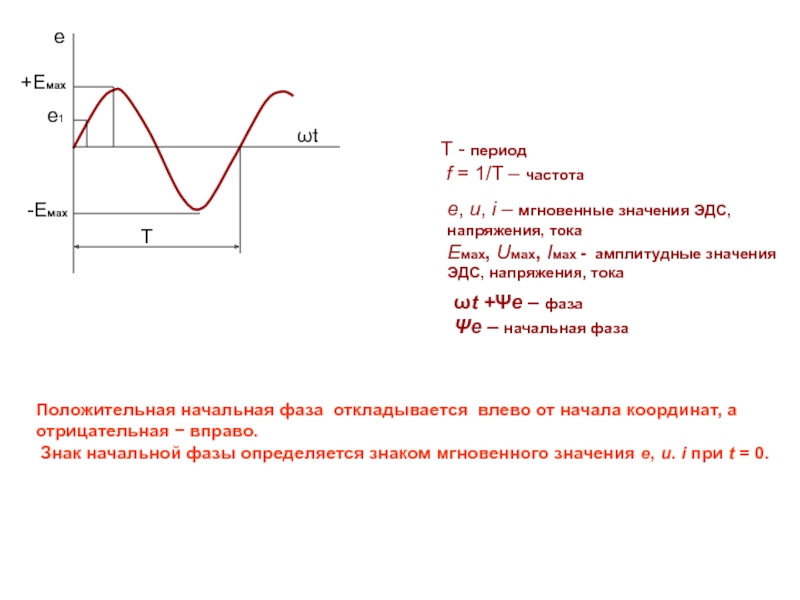
T - период
f = 1/T – частота
e,
Eмах, Uмах, Iмах - амплитудные значения ЭДС, напряжения, тока
ωt +Ψe – фаза
Ψe – начальная фаза
Положительная начальная фаза откладывается влево от начала координат, а
отрицательная − вправо.
Знак начальной фазы определяется знаком мгновенного значения e, u. i при t = 0.
Слайд 4
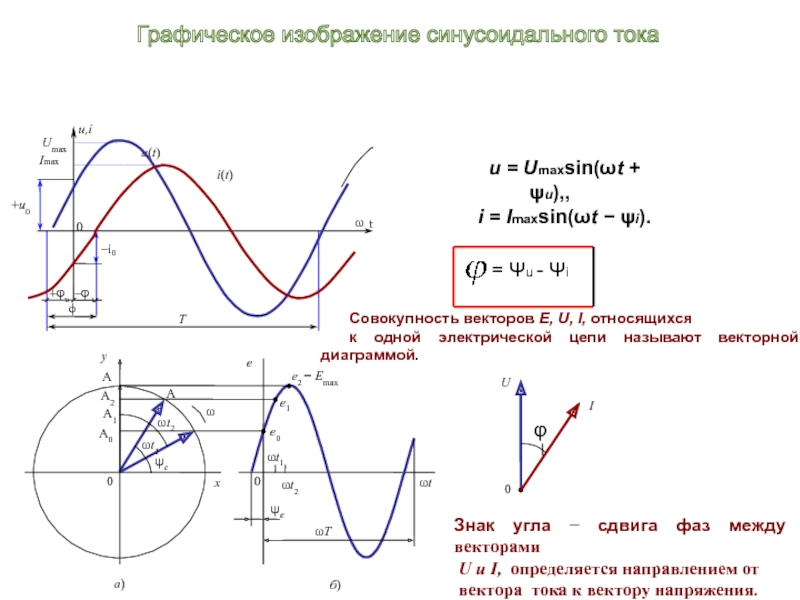
u = Umахsin(ωt + ψu),,
i = Imахsin(ωt − ψi).
=
Совокупность векторов E, U, I, относящихся
к одной электрической цепи называют векторной диаграммой.
Знак угла − сдвига фаз между векторами
U и I, определяется направлением от
вектора тока к вектору напряжения.
φ
Графическое изображение синусоидального тока
Слайд 5Действующим значением синусоидального тока называют такое значение
постоянного тока, при прохождении
сопротивлению R за время одного периода Т выделяется столько же теплоты,
сколько при прохождении синусоидального тока.
Количество теплоты Q, выделяемое в резисторе R за время Т при синусоидальном токе:
, а при постоянном токе:
;
;
Так как Qsin = Qпост, то
Действующие и средние значения синусоидальных ЭДС, напряжений
и токов
;
Слайд 6За среднее значение синусоидального тока принимают такое значение постоянного тока,
при
синусоидальном токе.
Iср = 0,637Imax
Uср = 0,637Umax
Eср = 0,637Emax
Слайд 7Синусоидальная величина изображается вращающимся вектором на комплексной плоскости с
осями ±1
− мнимая единица, символ.
Комплексные значения синусоидальных величин обозначают
несинусоидальных − z, S.
Над комплексными числами можно производить все алгебраические действия
(при сложении и вычитании удобнее использовать алгебраическую форму,
а при умножении, делении, возведении в степень, извлечении корня – показательную).
Алгебраическая форма записи:
.
Тригонометрическая форма записи:
İ = Icosψi + jIsinψi .
Показательная форма записи:
I − модуль действующего значения тока, равный длине вектора;
где
− действительная составляющая тока;
) – аргумент тока, равный начальной фазе, т. е.угол между вектором и действительной полуосью +1 при t = 0.
- мнимая составляющая тока
ψi = arctg (
)
При расчете цепей синусоидального тока (и простых, и сложных) все законы и методы расчета
цепей постоянного тока действительны при условии, что все величины сопротивлений,
напряжений и токов выражены в комплексных числах.
Комплексный метод расчета
Слайд 8Переход из одной формы записи в другую осуществляется по формуле Эйлера
Например:
i = 10cos37˚ + j10sin37º = 10 ·0,8 + j10 0,6 = 8 +j6 =
Умножение комплексного числа на + j приводит к увеличению его аргумента на 90º
и повороту вектора на 90º против часовой стрелки (в положительном направлении);
умножение на −j – к уменьшению аргумента на 90º и повороту вектора на 90º
в отрицательном направлении (по часовой стрелке).
При работе с комплексными числами используют и сопряженные комплексные
величины, имеющие одинаковые модули и одинаковые по величине, но противоположные
по знаку аргументы:
еjarctg6/8 = 10ej37°
Слайд 9
Закон Oма для участка цепи:
напряжения источников питания, расположенных в контуре;
Zk и İk − сопротивления и токи отдельных приемников энергии, расположенных в этом контуре.
Y = 1/Z =
где Y – комплексная полная проводимость,
Первый закон Кирхгофа:
İk = 0,
где İk − токи, сходящиеся в одном узле.
Второй закон Кирхгофа:
Zkİk,
=
Законы Ома и Кирхгофа в комплексной форме
Слайд 10
Для
цепь заменяют схемой замещения, составленной из так называемых
«идеальных» элементов:
резистивный элемент с активным сопротивлением R(Ом),или активной проводимостью G = 1/R(Cм);
индуктивный элемент с индуктивностью L (Гн) и реактивным индуктивным сопротивлением XL = 2πƒL(Ом ) или реактивной индуктивной проводимостью BL = 1/XL (См);
емкостный элемент с емкостью С, и реактивным емкостным сопротивлением XC = 1/2πƒC (Ом) или реактивной емкостной проводимостью BC = 1/XC,( (См).
При расчете цепей синусоидального тока (и простых, и сложных) все
законы и методы расчета цепей постоянного тока действительны при
условии, что все величины сопротивлений, напряжений и токов
выражены в комплексных числах.
Пассивные элементы в цепи синусоидального тока
Слайд 11
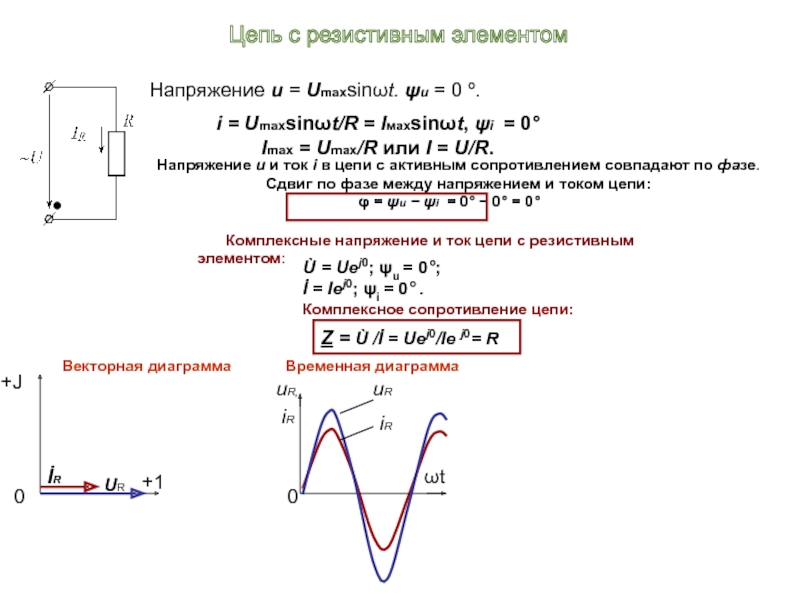
Напряжение u = Umахsinωt. ψu = 0 º.
i =
Imах = Umах/R или I = U/R.
Напряжение u и ток i в цепи с активным сопротивлением совпадают по фазе.
Сдвиг по фазе между напряжением и током цепи:
φ = ψu − ψi = 0° − 0° = 0°
Комплексные напряжение и ток цепи с резистивным элементом:
Ù = Uej0; ψu = 0°;
İ = Iej0; ψi = 0° .
Комплексное сопротивление цепи:
Z = Ù /İ = Uej0/Ie j0= R
+1
+J
0
İR
UR
iR
uR
uR,
iR
0
ωt
Цепь с резистивным элементом
Временная диаграмма
Векторная диаграмма
Слайд 12
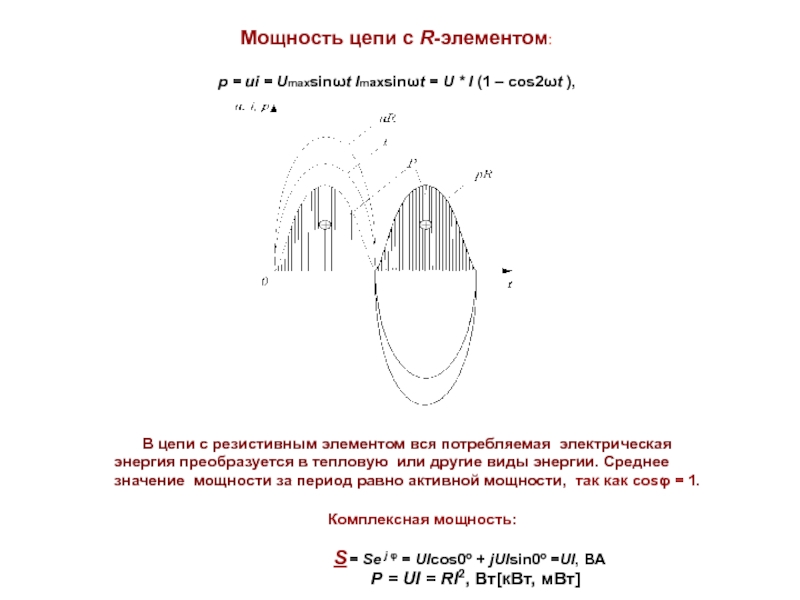
Мощность цепи с R-элементом:
p = ui = Umахsinωt Imахsinωt = U
В цепи с резистивным элементом вся потребляемая электрическая энергия преобразуется в тепловую или другие виды энергии. Среднее значение мощности за период равно активной мощности, так как cosφ = 1.
Комплексная мощность:
= Se j φ = UIcos0º + jUIsin0º =UI, ВА
Р = UI = RI2, Вт[кВт, мВт]
S
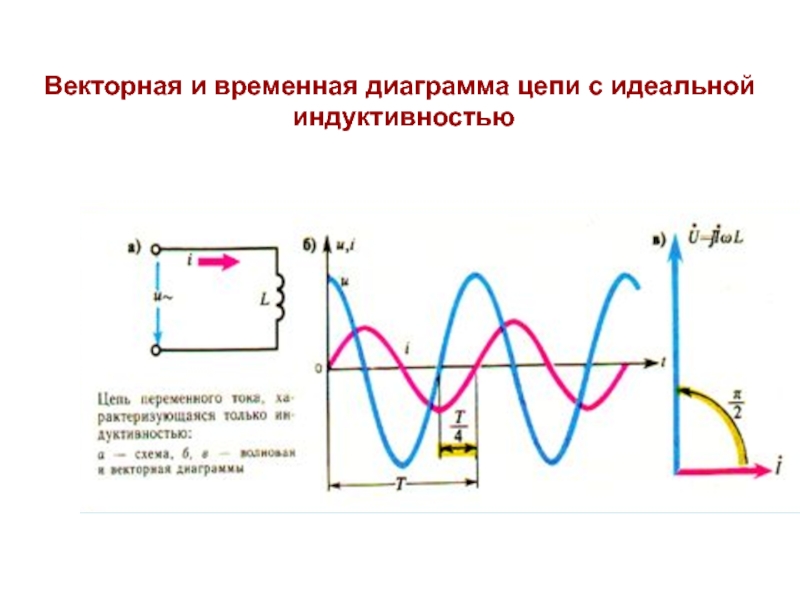
Слайд 13Напряжение u = Umахsinωt
еL = −wdФ/dt = −Ldi/dt,
u − uL
Umах sinωt – Ldi/dt = 0, или di/dt = Umахsinωt/L.
i = − Umахcosωt/ωL = Umахsin(ωt − π/2)/ωL = Imахsin(ωt − π/2).
Величина ωL имеет размерность сопротивления, Гн/с = В·с/А·с = Ом.
Это индуктивное сопротивление:XL = ωL = 2πfL.
Ù = Ue j0, ψu = 0o; İ = Ie −j90, ψi = −90°
φ = 0° – (−90° ) = +90o
Ù /İ = Ue j0/Ie −j90 = XLej90 = jXL;
=
Цепь с индуктивным элементом
Таким образом, синусоида тока в цепи с идеальной индуктивной катушкой
отстает от синусоиды напряжения на угол 90º.
Сдвиг по фазе между напряжением и током цепи:
Слайд 15
P = ui = Umахsinωt * I mахsin(ωt − 90°) =
Энергия обмена энергией между источником и приемником, которая не преобразуется в
другие виды энергии, называется реактивной. Интенсивность обмена энергией
характеризуется реактивной мощностью QL = UI,вар [квар, мвар]
= Sejφ = UIcos90° + jUIsin90° = jUI
QL = UI = XLI2, вар[квар,мвар]
S =
Мощность в цепи с идеальной индуктивной катушкой
Слайд 16
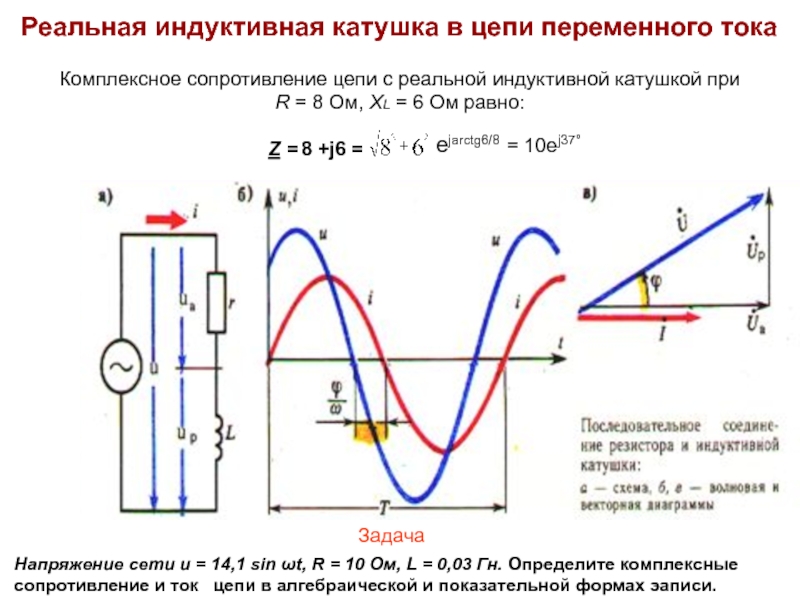
Комплексное сопротивление цепи с реальной индуктивной катушкой при
R = 8 Ом,
Реальная индуктивная катушка в цепи переменного тока
Напряжение сети u = 14,1 sin ωt, R = 10 Ом, L = 0,03 Гн. Определите комплексные сопротивление и ток цепи в алгебраической и показательной формах эаписи.
Задача
8 +j6 =
еjarctg6/8 = 10ej37°
Z =
Слайд 17
.
По II ЗК Кирхгофа: u = uc.
u = Umахsinωt,
Q
i = dQ/dt = ωCUmахcosωt = ωCUmахsin(ωt + π/2) = Imахsin(ωt + π/2),
Imах = ωCUmах = Umах/(1/ωC).
Величина 1/ωC имеет размерность сопротивления,
[с/Ф = сВ/Кл = = сВ/сА = Ом]. Это емкостное сопротивление
Xс = 1/ωC = 1/2πfC.
= Uej0; ψu = 0º;
İ = Ie j90;; ψi = + 90º;
= Ù /İ
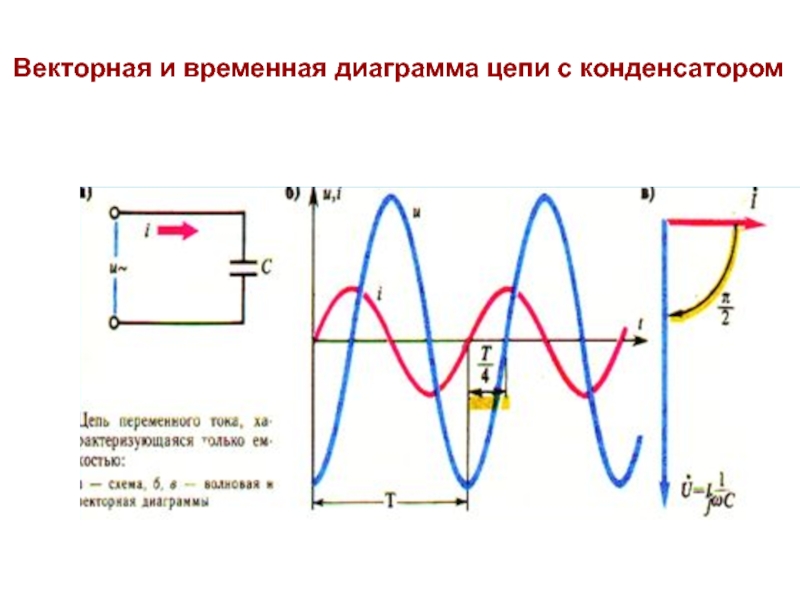
Цепь с конденсатором
Таким образом, синусоида тока в цепи с конденсатором опережает синусоиду напряжения на угол 90º.
φ = ψu − ψi = 0º − 90º = − 90º.
Сдвиг по фазе между напряжением и током цепи:
Слайд 19Р = ui = Uмахsinωt * I mахsin(ωt + 90°) =
Энергия обмена энергией между источником и приемником, которая не преобразуется в
другие виды энергии, называется реактивной. Интенсивность обмена энергией
характеризуется реактивной мощностью Qс = – UI,вар [квар, мвар]
= =Se−jϕ = UIcos90° – jUIsin90°= – jUI
Qc = –UI= –ХсI2, вар
S =
Мощность цепи с конденсатором
Слайд 20
u = UmахRsinωt + UmахLsin(ωt + π/2) +
+UmахC sin(ωt −
i = Iмахsinωt
u = uR + uL + uC
Полное напряжение цепи состоит из двух синусоидальных слагаемых одинаковой
частоты, а, следовательно, являются так же синусоидальными с некоторой
амплитудой Umах и фазовым углом φ (при условии, что начальная фаза тока равна 0).
u = Umахsin(ωt+φ).
XL>XC и
I
+1
+j
U L
UR
U
UP = UL - UC
UC
φ
Ψi= 0
UC
UR
Последовательное соединение R, L, C
Векторная диаграмма для цепи с последовательным соединением R, L, C при
Слайд 21 = IR + I jXL − I jXC = I[(R
Z =
сопротивление цепи
φ = arctg(XL – XC) / R
XL − XC – реактивное сопротивление цепи
I = U/z – ток цепи
Модуль комплексного
сопротивления - полное
Аргумент комплексного сопротивления цепи – сдвиг по фазе синусоид напряжения и тока
Комплексное напряжение цепи
j
φ
Слайд 22Z = U/I
R = UR/I
X = (UL – UC)/I
φ
φ
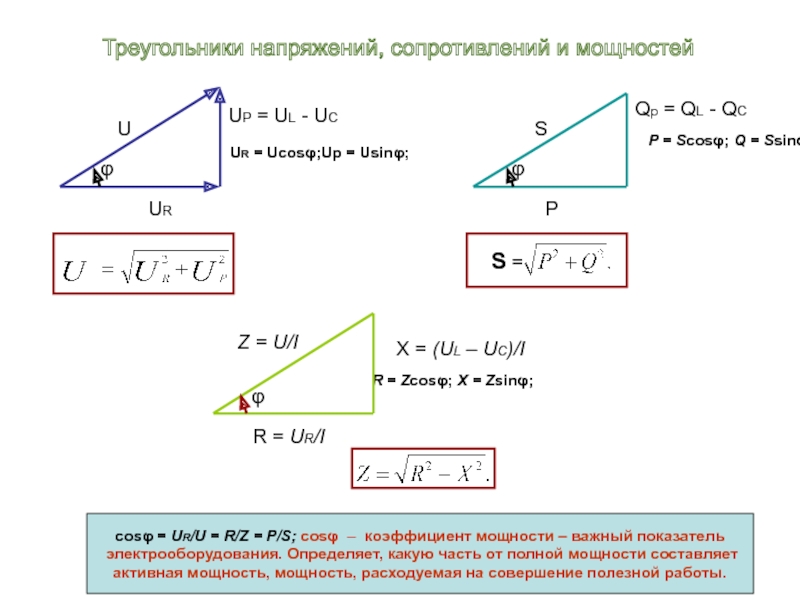
R = Zcosφ;
P = Scosφ; Q = Ssinφ;
cosφ = UR/U = R/Z = P/S; cosφ – коэффициент мощности – важный показатель
электрооборудования. Определяет, какую часть от полной мощности составляет
активная мощность, мощность, расходуемая на совершение полезной работы.
φ
U
UR
UP = UL - UC
UR = Ucosφ;Up = Usinφ;
S
P
Qр = QL - QC
Треугольники напряжений, сопротивлений и мощностей
S =
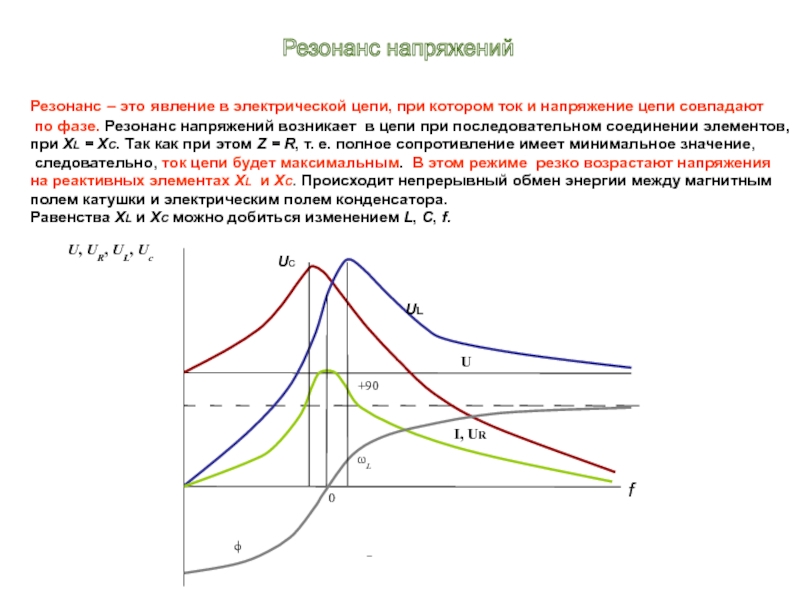
Слайд 23Резонанс – это явление в электрической цепи, при котором ток и
по фазе. Резонанс напряжений возникает в цепи при последовательном соединении элементов,
при XL = XC. Так как при этом Z = R, т. е. полное сопротивление имеет минимальное значение,
следовательно, ток цепи будет максимальным. В этом режиме резко возрастают напряжения
на реактивных элементах XL и XC. Происходит непрерывный обмен энергии между магнитным
полем катушки и электрическим полем конденсатора.
Равенства ХL и XC можно добиться изменением L, C, f.
f
Резонанс напряжений
Слайд 24Параллельное соединение R, L, C
U = Umaxsinωt
i L = ImахLsin(ωt − π/2);
i C = ImахCsinωt(ωt + π/2).
IR =U/R=GU; IL=U/XL = BLU; IC = U/XC = BCU.
где G = 1/R; BL = 1/XL; BC = 1/XC, Y = 1/Z
– активная, индуктивная, емкостная и
полная проводимости цепи.
I = U/Z =YU, А
Слайд 25
,
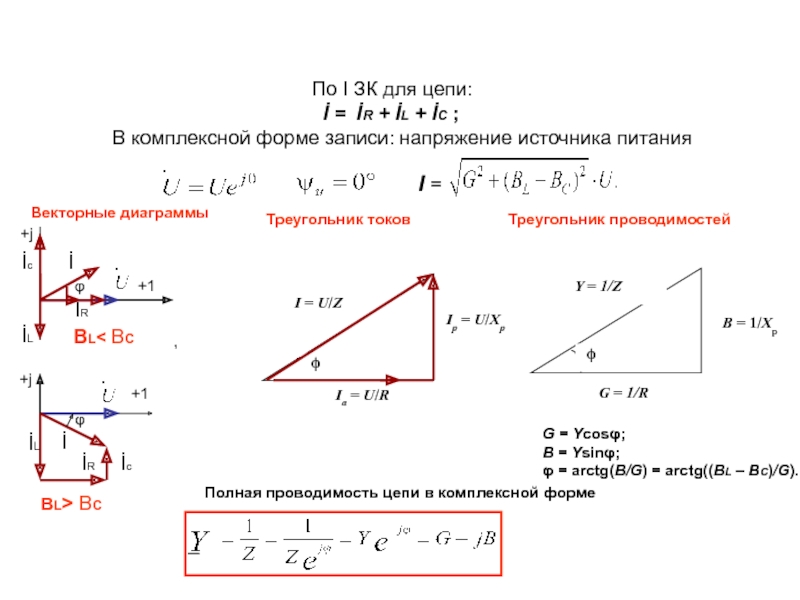
İ = İR + İL + İС ;
В комплексной форме записи: напряжение источника питания
+j
+1
İR
İL
İc
İ
φ
Треугольник токов
Треугольник проводимостей
G = Ycosφ;
B = Ysinφ;
φ = arctg(B/G) = arctg((BL – BC)/G).
I =
_
+1
+j
İR
İL
İc
Векторные диаграммы
Полная проводимость цепи в комплексной форме
ВL> ВC
ВL< ВC
İ
φ
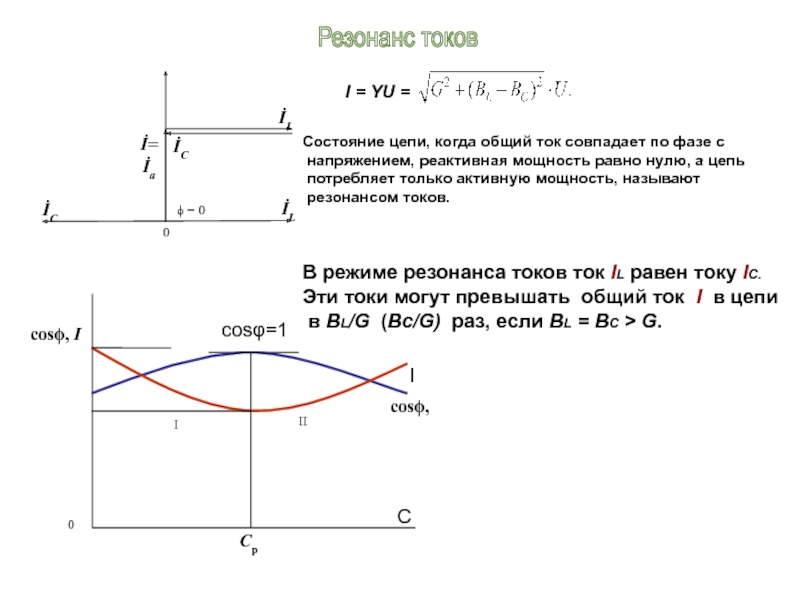
Слайд 26I = YU =
ϕ = 0
Состояние цепи, когда общий ток
напряжением, реактивная мощность равно нулю, а цепь
потребляет только активную мощность, называют
резонансом токов.
В режиме резонанса токов ток IL равен току IC.
Эти токи могут превышать общий ток I в цепи
в BL/G (Bc/G) раз, если BL = BC > G.
I
cosφ=1
Резонанс токов
С
Слайд 27
Y1 = 1/Z1 = 1/(R1+jX1)= (R1 − jXL)/(R1 + jXL)
Активная проводимость.
Индуктивная проводимость:
Полная проводимость ветви с R и C
Y2 = 1/Z2 = 1/( R2 – jXC) = (R2+JXC)/[(R2− jXC)(R2 + jXC)] =
Емкостная проводимость
Комплексный ток цепи:
Полная проводимость ветви с R и L
Полная проводимость всей цепи при BL > BC:
=
Активная проводимость
Параллельное соединение ветвей с разным характером нагрузки
2
−jφ
Y= Y1 + Y2 = (G1 + G2)+ j(BC – BL) = Y е
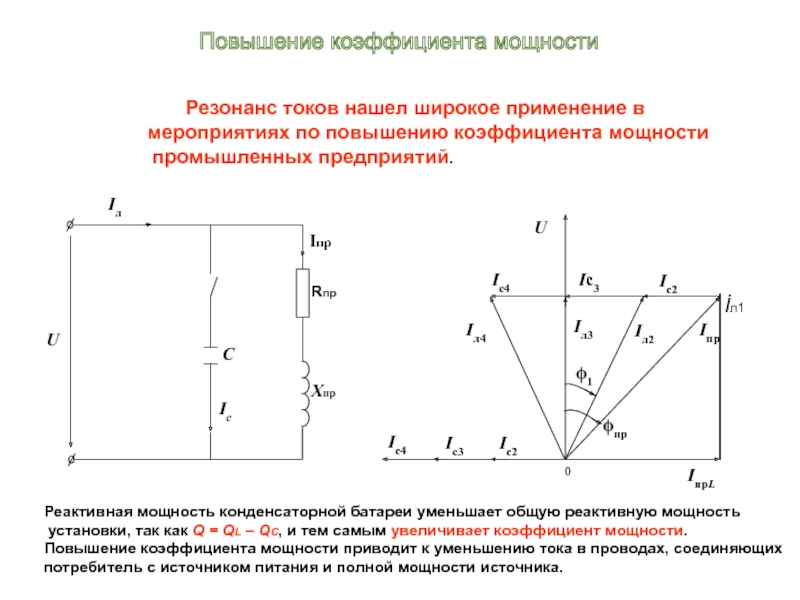
Слайд 28 Резонанс токов нашел широкое применение в
мероприятиях
промышленных предприятий.
Реактивная мощность конденсаторной батареи уменьшает общую реактивную мощность
установки, так как Q = QL – QC, и тем самым увеличивает коэффициент мощности.
Повышение коэффициента мощности приводит к уменьшению тока в проводах, соединяющих
потребитель с источником питания и полной мощности источника.
İл1
Повышение коэффициента мощности
Слайд 29
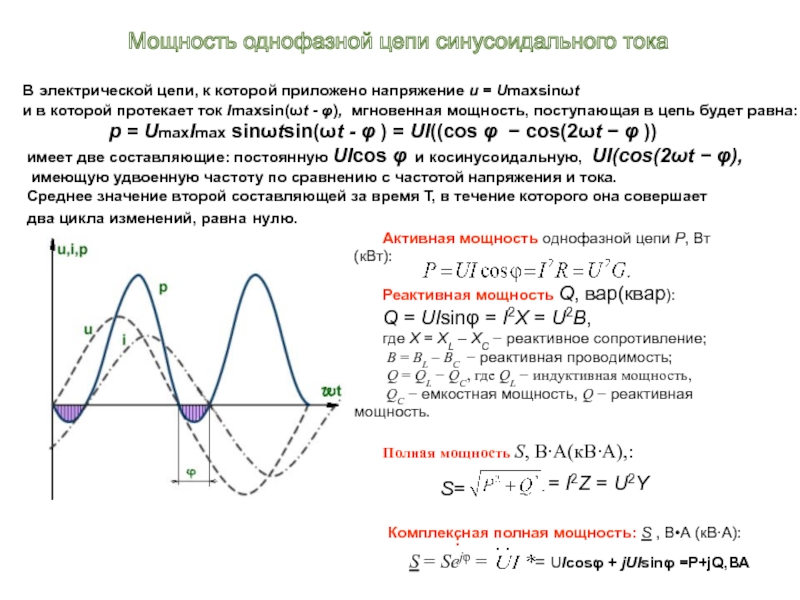
В электрической цепи, к которой приложено напряжение u = Umaxsinωt
и
р = UmaxImax sinωtsin(ωt - φ ) = UI((cos φ − cos(2ωt − φ ))
имеет две составляющие: постоянную UIcos φ и косинусоидальную, UI(cos(2ωt − φ),
имеющую удвоенную частоту по сравнению с частотой напряжения и тока.
Среднее значение второй составляющей за время Т, в течение которого она совершает
два цикла изменений, равна нулю.
Активная мощность однофазной цепи P, Вт (кВт):
Реактивная мощность Q, вар(квар):
Q = UIsinφ = I2X = U2B,
где X = XL – XC − реактивное сопротивление;
B = BL – BC − реактивная проводимость;
Q = QL − QC, где QL − индуктивная мощность,
QC − емкостная мощность, Q − реактивная мощность.
Полная мощность S, В∙А(кВ∙А),:
:
S = Sejφ =
= UIcosφ + jUIsinφ =P+jQ,ВА
Комплексная полная мощность: S , В•А (кВ∙А):
Мощность однофазной цепи синусоидального тока
S=
= I2Z = U2Y
Слайд 30
Расчет электрической цепи комплексным методом ведут в следующей
последовательности:
1) определяют комплексные
2) в зависимости от типа электрической цепи выбирают метод расчета цепи
(если цепь простая – метод свертывания; сложная – какой-либо из методов
расчета сложных цепей);
3) определяют токи и напряжения ветвей;
4) правильность расчета проверяют составлением баланса активных и реактивных
мощностей:
Рист = Σ Рпр , Qист = Σ Qпр, Sист =
I* = Pист ± jQист ,
Методика расчета однофазных цепей синусоидального тока
Слайд 311. Катушка индуктивности L = 0,032 Гн подключена к источнику питания
f = 50 Гц. Вычертить электрическую схему цепи, определить ток, мощность и
построить векторную диаграмму, если начальная фаза напряжения ψU = 30°.
2. Конденсатор С = 600 мкФ подключен к источнику питания U = = 40В, f = 50 Гц.
Вычертить электрическую схему цепи, определить ток, мощность и построить
векторную диаграмму, если начальная фаза тока ψi = – 30°.
3. В цепь синусоидального тока частотой f = 50 Гц последовательно включены
R1 = 50 м, R2 = 40 м, L = 0,096 Гц, С = 630 мкФ. Напряжение на конденсаторе
Uc = 30 В. Определить ток, активную, реактивную и полную мощность цепи.
Вычертить электрическую схему цепи и построить векторную диаграмму, если
начальная фаза тока ψi = – 45º.
4. В цепь синусоидального тока f = 50 Гц параллельно включены две ветви
с параметрами R1 = 8 Ом; L1 = 0,016 Гн; R2 = 4 Ом; С2 = 680 мкФ.
Напряжение на R2 = 40 В. Вычертить электрическую схему, определить токи в
ветвях. Построить векторную диаграмму, если начальная фаза напряжения
источника питания ψu = 0.
Задачи












![= IR + I jXL − I jXC = I[(R + j(XL − XC)]](/img/tmb/5/413702/4b2fe119d536cc9c5921aee57432de98-800x.jpg)