- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Возможности восстановления смазанных космических изображений презентация
Содержание
- 1. Возможности восстановления смазанных космических изображений
- 2. Источники «смаза» космических изображений Задача движение
- 3. -
- 4. Особенность задачи Слепые: решить задачу при неизвестной
- 5. Инверсная фильтрация - исходное уравнение в
- 6. Винеровская фильтрация
- 7. Фильтрация Тихонова где
- 8. Тестовое изображение Элемент: 1 пиксел Элемент: 2 пиксела Элемент: 8 пиксела Элемент: 4 пиксела
- 9. Смазанное изображение (ширина ФРТ 2σ = 1,5
- 10. Смазанное изображение (ширина ФРТ 2σ = 2
- 11. Смазанное изображение (ширина ФРТ 2σ = 2,5
- 12. Смазанное изображение (ширина ФРТ 2σ = 3
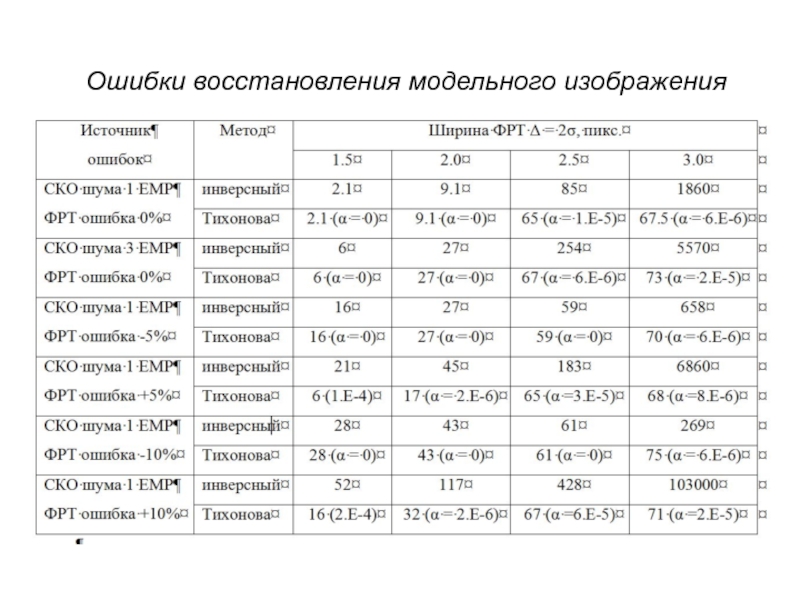
- 13. Ошибки восстановления модельного изображения
- 14. Изображение Луны, полученное УТК-ТСНН (2σx = 1.96, 2σy = 1.70)
- 15. Изображение Луны после фильтрации Тихонова (α = 1.Е-4)
- 16. до фильтрации после фильтрации Фрагмент изображения Луны
- 17. до фильтрации после фильтрации Фрагмент изображения Луны
- 18. Заключение Результаты анализа тестового изображения показывают, что
Слайд 1Возможности восстановления смазанных космических изображений
Б.С. Жуков
Институт космических исследований РАН
Слайд 2Источники «смаза» космических изображений
Задача
движение носителя,
дефокусировка,
разрешение объектива хуже разрешения
суб-пиксельное подсканирование (супер-разрешение)
Устранить смаз
Слайд 3
- поле яркости,
- непрерывная функция рассеяния точки (ФРТ) съемочной системы,
- цифровое изображение,
- координаты центра пиксела (i,j)
где:
- дискретная аппроксимация ФРТ
Дискретная аппроксимация:
- идеальное изображение (усреднение поля яркости по площади пиксела)
Решить уравнение (1) относительно идеального изображения
Модель формирования цифрового изображения:
где:
Математическая формулировка задачи
Задача:
(1)
- шум,
Слайд 4Особенность задачи
Слепые: решить задачу при неизвестной ФРТ
Классические: решить задачу при заданной
Инверсная и винеровская фильтрация, фильтрация Тихонова, метод Ричардсона-Люси и др.
относится к классу некорректных задач, решение которых неустойчиво: при наличии даже небольшого шума возможны большие отклонения восстановленного изображения от идеального
Методы решения
задача решения уравнения
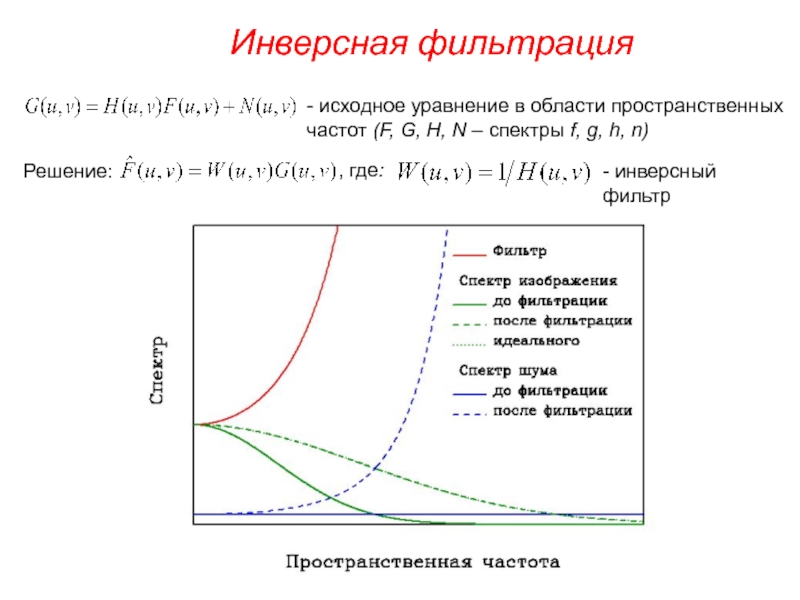
Слайд 5Инверсная фильтрация
- исходное уравнение в области пространственных частот (F, G, H,
Решение:
, где:
- инверсный фильтр
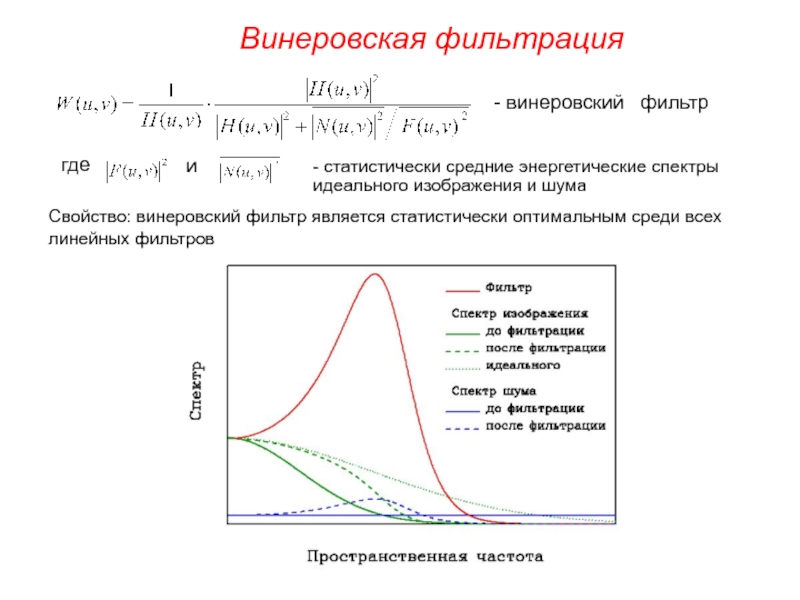
Слайд 6Винеровская фильтрация
идеального изображения и шума
и
- статистически средние
Свойство: винеровский фильтр является статистически оптимальным среди всех линейных фильтров
где
- винеровский фильтр
Слайд 7Фильтрация Тихонова
где
При α = 0 фильтрация Тихонова сводится к инверсной
α – подбираемый параметр.
- фильтр Тихонова
Слайд 9Смазанное изображение (ширина ФРТ 2σ = 1,5 пиксела,
После инверсной фильтрации
Слайд 10Смазанное изображение (ширина ФРТ 2σ = 2 пиксела,
После инверсной фильтрации
Слайд 11Смазанное изображение (ширина ФРТ 2σ = 2,5 пиксела,
После инверсной фильтрации
После фильтрации Тихонова (α = 1.Е-5)
Слайд 12Смазанное изображение (ширина ФРТ 2σ = 3 пиксела,
После инверсной фильтрации
После фильтрации Тихонова (α = 6.Е-6)
Слайд 18Заключение
Результаты анализа тестового изображения показывают, что при низком уровне шума (1:250
Метод Тихонова требует подбора параметра α в зависимости от уровня шума и точности знания ФРТ съемочной системы и поэтому хорошо подходит для интерактивного режима обработки изображений.
Возможность использования метода в автоматическом режиме (например, при потоковой обработки изображений КМСС) требует дополнительных исследований.