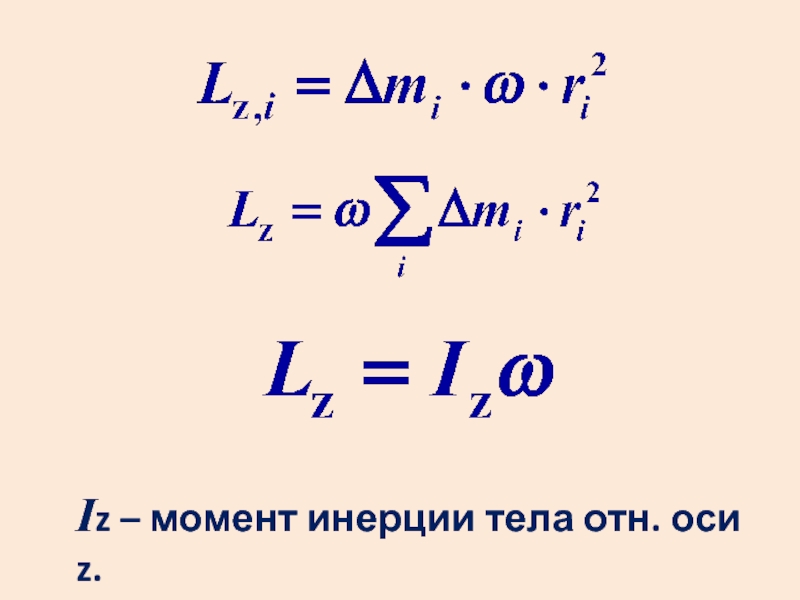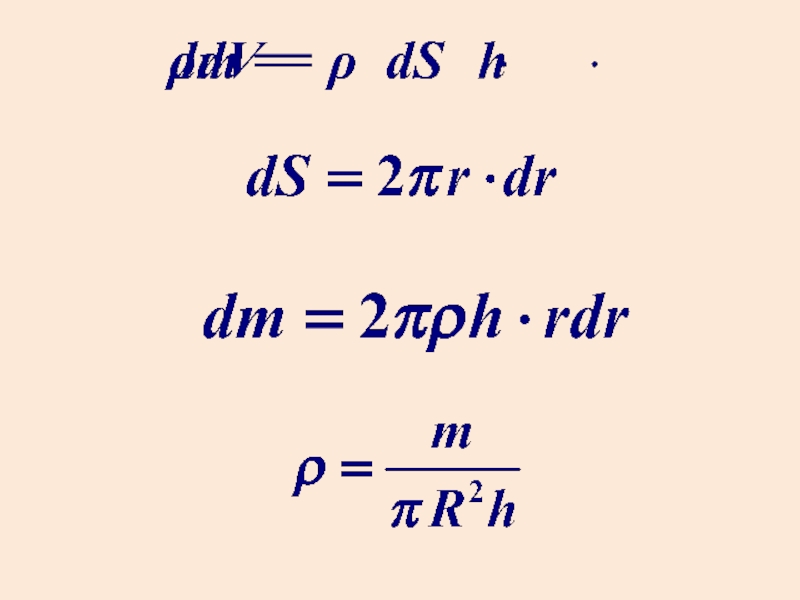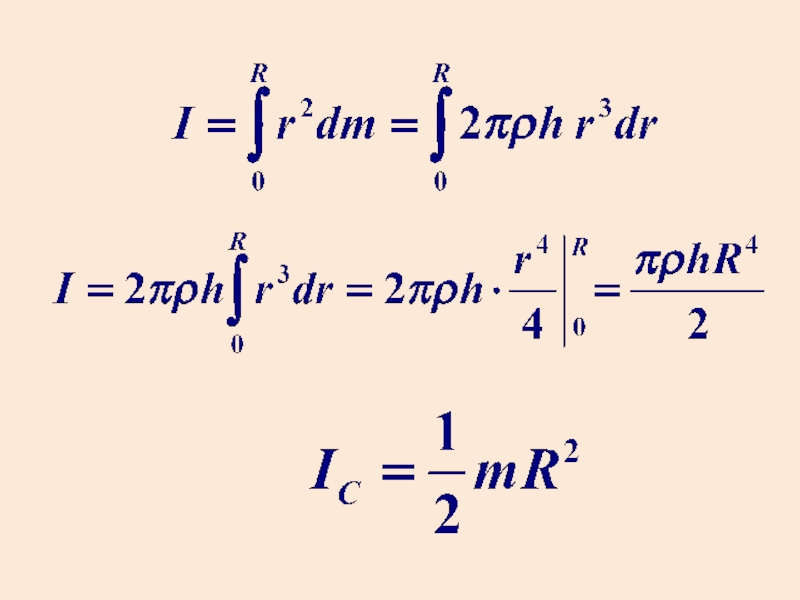- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика вращательного движения. Момент силы презентация
Содержание
- 1. Динамика вращательного движения. Момент силы
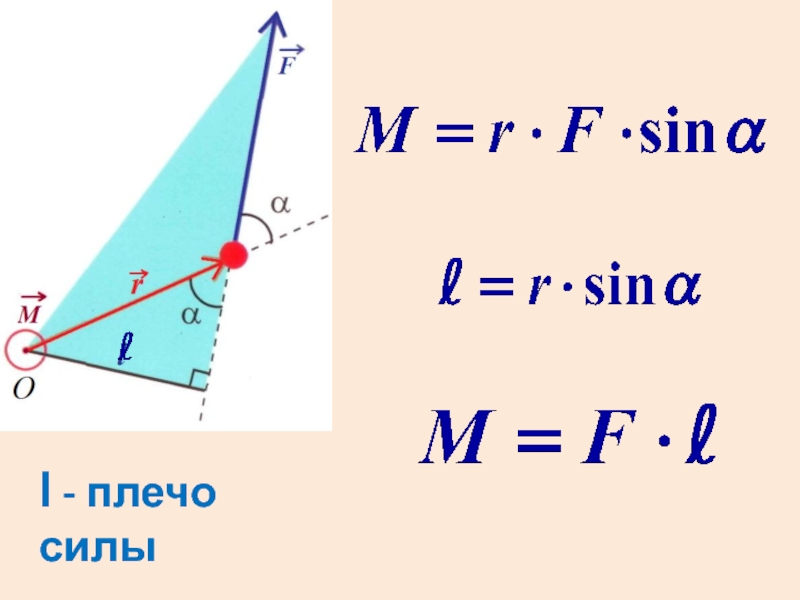
- 2. Момент силы, взятый относительно точки О, находится
- 3. l - плечо силы
- 4. Направление вектора момента силы находим по правилу
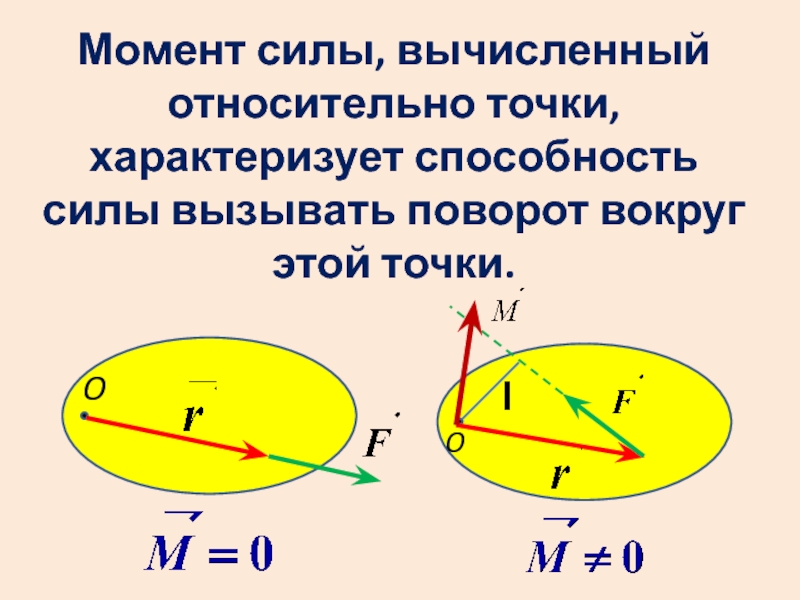
- 5. Момент силы, вычисленный относительно точки, характеризует способность
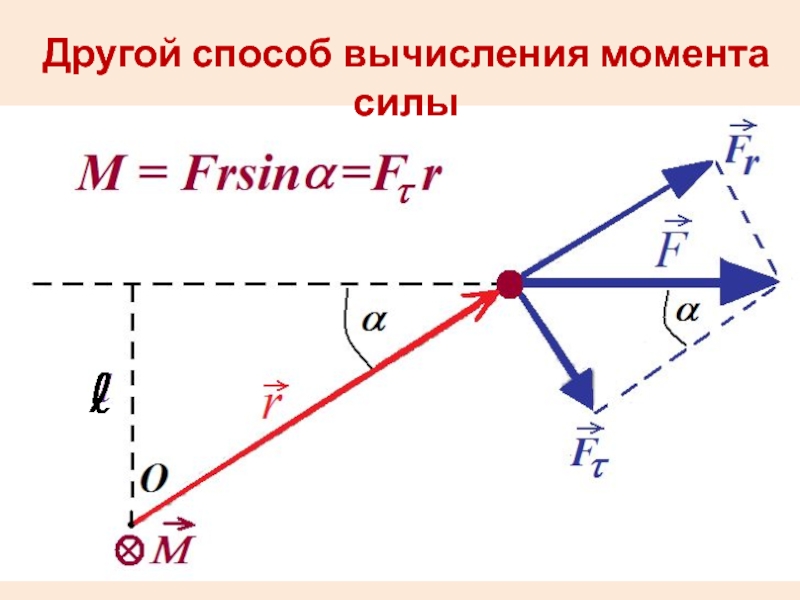
- 6. Другой способ вычисления момента силы
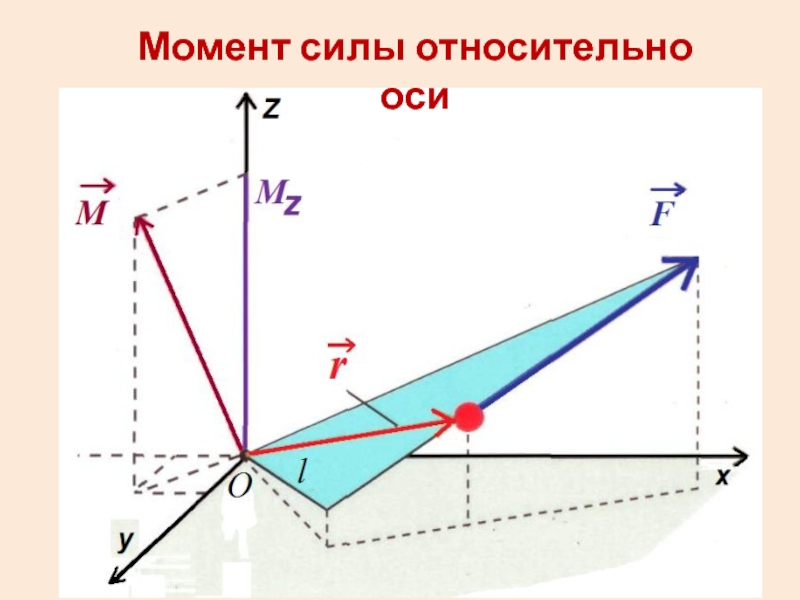
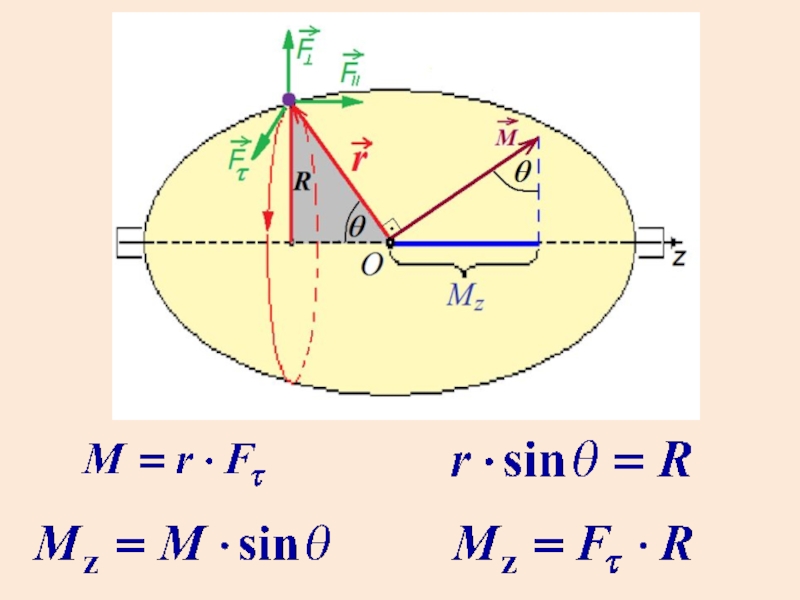
- 7. Момент силы относительно оси
- 8. Момент силы относительно оси z – это
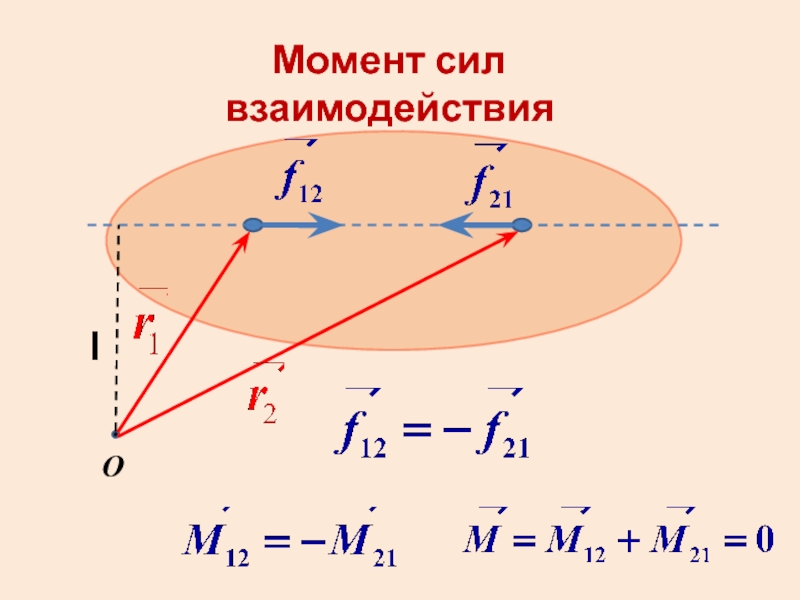
- 10. Момент сил взаимодействия l O
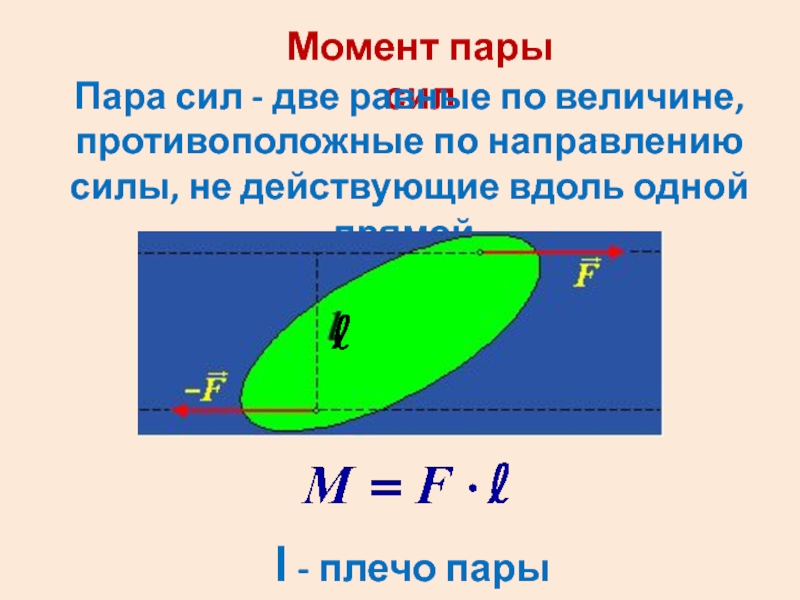
- 11. Момент пары сил Пара сил -
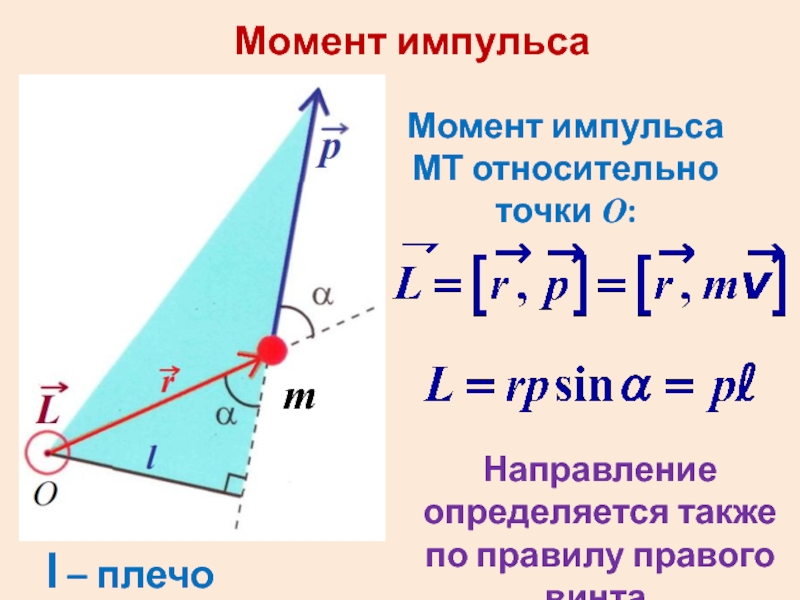
- 12. Момент импульса l – плечо импульса
- 13. Момент импульса относительно оси вращения
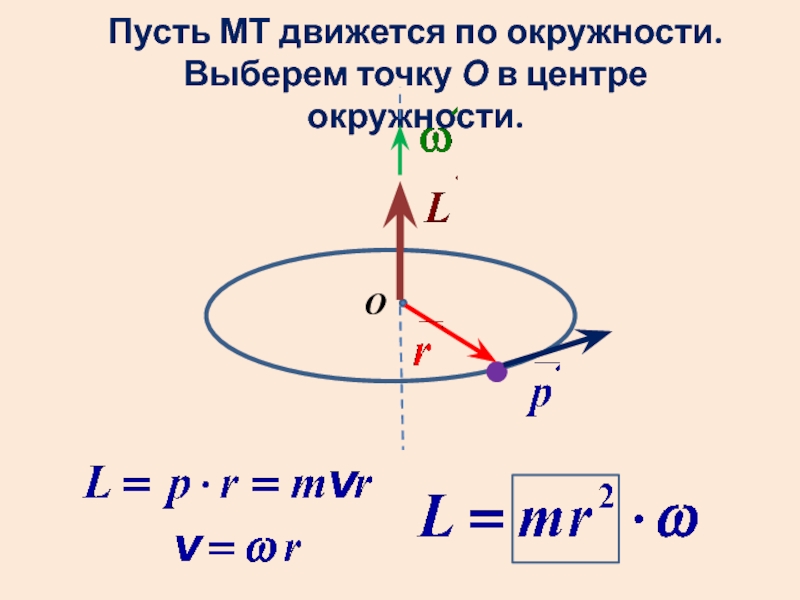
- 14. Пусть МТ движется по окружности. Выберем точку
- 15. Моментом инерции МТ называют произведение ее массы на квадрат расстояния до оси вращения.
- 16. [ I ] = кг ·
- 17. Момент инерции твердого тела Момент инерции тела
- 18. Момент импульса твердого тела Разобьем тело на
- 19. Iz – момент инерции тела отн. оси z.
- 20. Для однородного симметричного тела, вращающегося вокруг оси
- 21. Момент инерции тела определяется его размерами, формой,
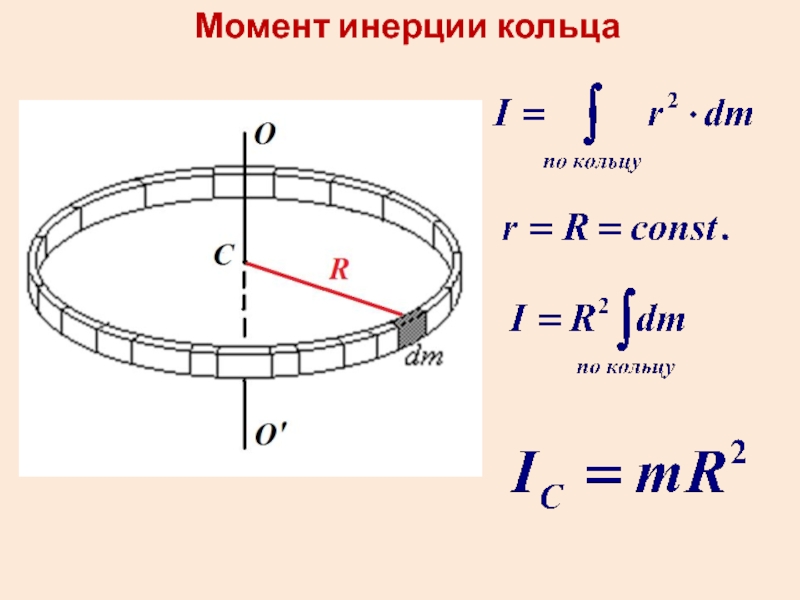
- 22. Момент инерции кольца
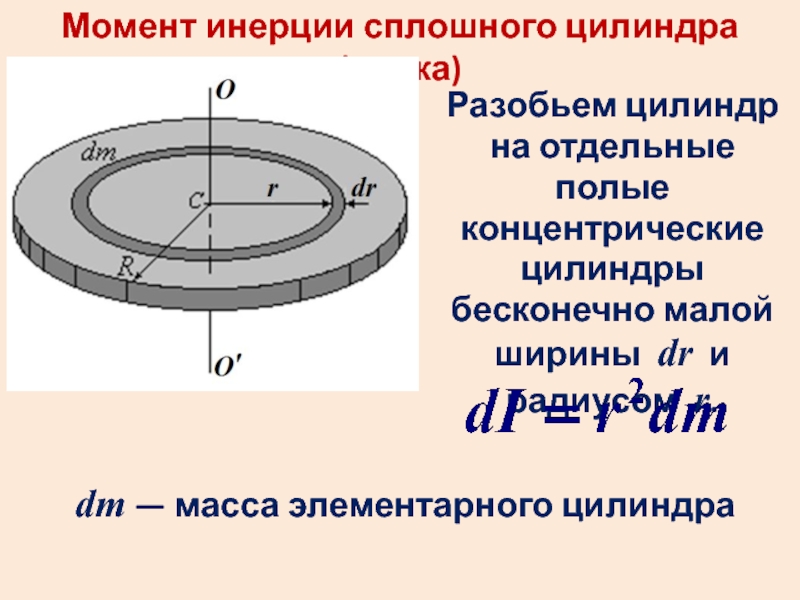
- 23. Момент инерции сплошного цилиндра (диска) Разобьем
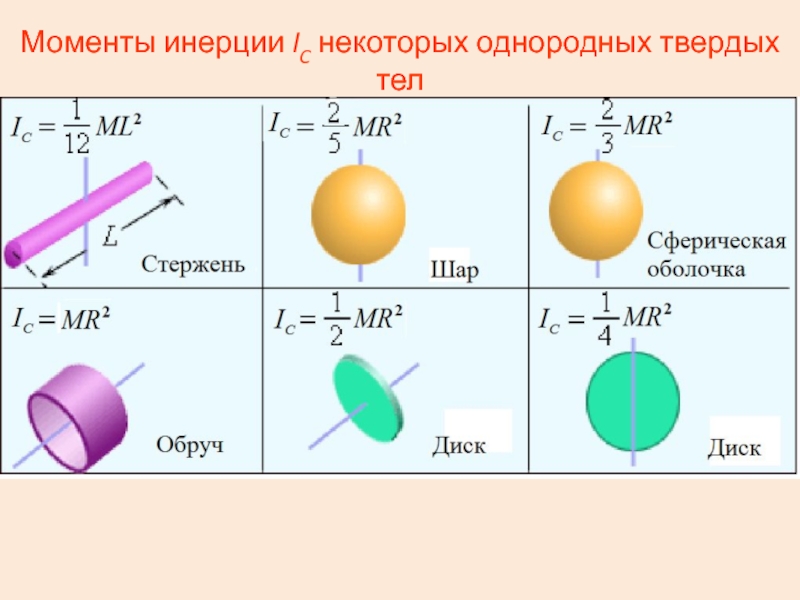
- 26. Моменты инерции IC некоторых однородных твердых тел
- 27. Теорема Штейнера Момент инерции относительно произвольной
- 28. Применение теоремы Штейнера Для стержня Найдем момент инерции стержня относительно оси, проходящей через его конец:
Момент силы, взятый относительно точки О, находится как векторное произведение радиус-вектора, проведенного из точки О в точку приложения силы, на эту силу.
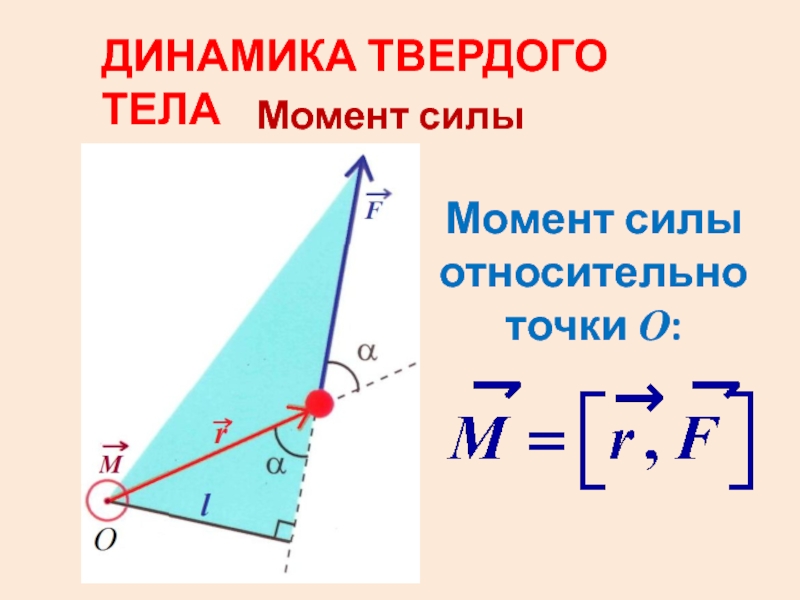
Слайд 2Момент силы, взятый относительно точки О, находится как векторное произведение радиус-вектора,
проведенного из точки О в точку приложения силы, на эту силу.
Слайд 4Направление вектора момента силы находим по правилу правого винта.
Этот вектор перпендикулярен
и силе, и радиус-вектору.
Слайд 5Момент силы, вычисленный относительно точки, характеризует способность силы вызывать поворот вокруг
этой точки.
O
O
l
Слайд 8Момент силы относительно оси z – это скалярная величина, равная проекции
на ось z вектора , найденного относительно произвольной точки этой оси.
Слайд 11Момент пары сил
Пара сил - две равные по величине, противоположные
по направлению силы, не действующие вдоль одной прямой.
l - плечо пары
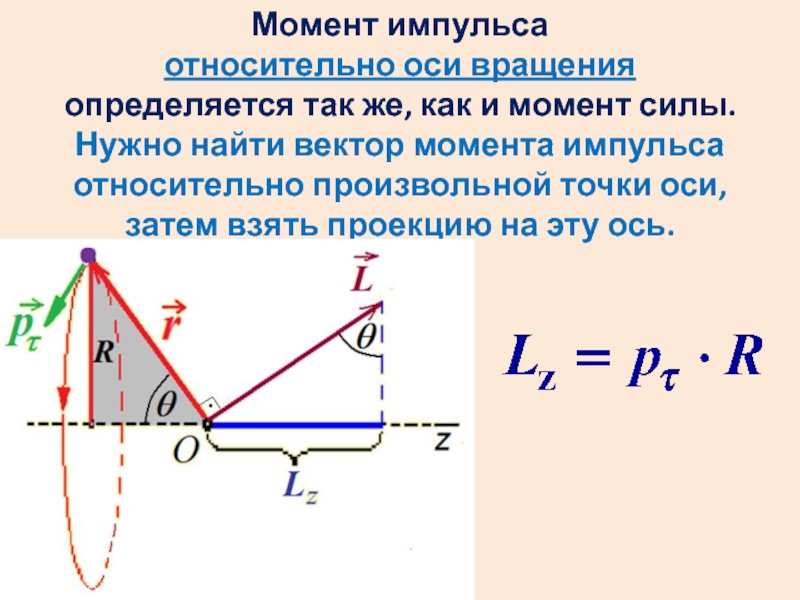
Слайд 12Момент импульса
l – плечо импульса
Момент импульса МТ относительно точки О:
Направление определяется
также по правилу правого винта.
m
Слайд 13Момент импульса
относительно оси вращения
определяется так же, как и момент
силы.
Нужно найти вектор момента импульса относительно произвольной точки оси, затем взять проекцию на эту ось.
Нужно найти вектор момента импульса относительно произвольной точки оси, затем взять проекцию на эту ось.
Слайд 17Момент инерции твердого тела
Момент инерции тела относительно данной оси – это
величина, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси.
или
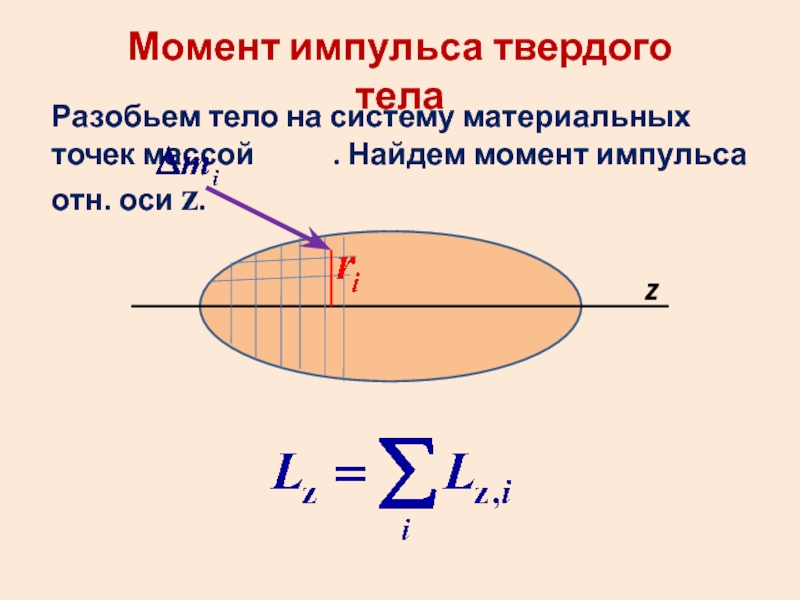
Слайд 18Момент импульса твердого тела
Разобьем тело на систему материальных точек массой
. Найдем момент импульса отн. оси z.
z
Слайд 20Для однородного симметричного тела, вращающегося вокруг оси симметрии, справедливо векторное равенство:
I
– момент инерции тела относительно оси симметрии
Слайд 21Момент инерции тела определяется его размерами, формой, распределением и величиной массы,
а также положением оси вращения.
Слайд 23Момент инерции сплошного цилиндра (диска)
Разобьем цилиндр на отдельные полые концентрические
цилиндры бесконечно малой ширины dr и радиусом r.
dm — масса элементарного цилиндра
Слайд 27Теорема Штейнера
Момент инерции относительно произвольной оси вращения равен сумме момента
инерции тела относительно параллельной оси вращения, проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями.
Слайд 28Применение теоремы Штейнера
Для стержня
Найдем момент инерции стержня относительно оси, проходящей через
его конец:
