- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Динамика колебаний. (Раздел 2. Тема 8) презентация
Содержание
- 1. Динамика колебаний. (Раздел 2. Тема 8)
- 2. Тема 8. Динамика колебаний 1. Дифференциальное уравнение
- 3. 1 учебный вопрос: Уравнение гармонического осциллятора. (1)
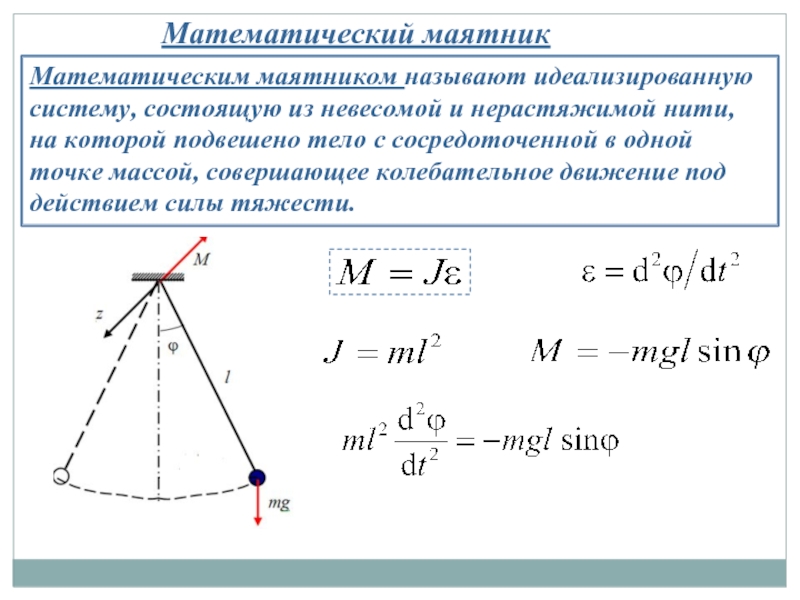
- 4. Математический маятник Математическим маятником называют идеализированную систему,
- 5. сравниваем с
- 6. Физическим маятником называется любое твердое тело, способное
- 7. Решение дифференциального уравнения колебаний физического маятника (5)
- 8. Приведенной длиной физического маятника называется длина такого
- 9. 2 учебный вопрос: Свободные затухающие колебания
- 10. β - коэф.затухания; ω0 - частота собственных
- 11. Характеристики затухания системы 2. Коэффициент затухания β
- 12. 5. Добротность колебательной системы - число полных
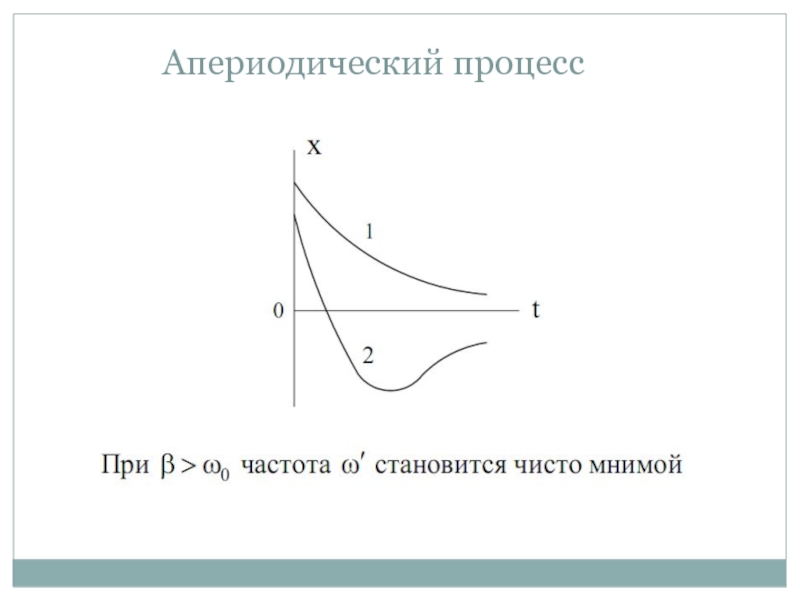
- 13. Апериодический процесс
- 14. 3 учебный вопрос: Вынужденные колебания. Резонанс. Пусть
- 15. Решение: (11)
- 16. - резонанс резонансная кривая
Слайд 2Тема 8. Динамика колебаний
1. Дифференциальное уравнение колебаний. Математический и физический маятники.
2.
3. Вынужденные колебания. Резонанс.
Слайд 4Математический маятник
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой
Слайд 5
сравниваем с
Решение:
Период колебаний математического маятника зависит только от ускорения свободного
(2)
(3)
(4)
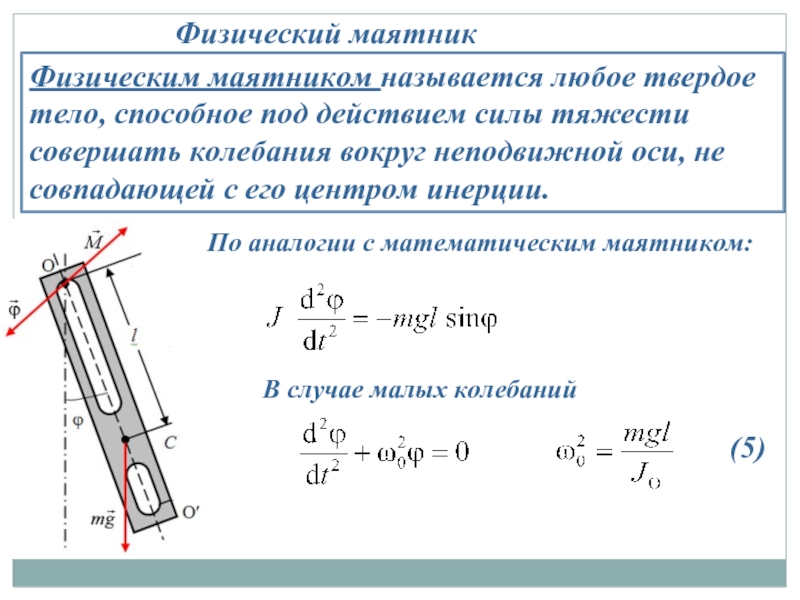
Слайд 6Физическим маятником называется любое твердое тело, способное под действием силы тяжести
Физический маятник
По аналогии с математическим маятником:
В случае малых колебаний
(5)
Слайд 7Решение дифференциального уравнения колебаний физического маятника (5) имеет вид
(6)
Сравним физический маятник
маятником
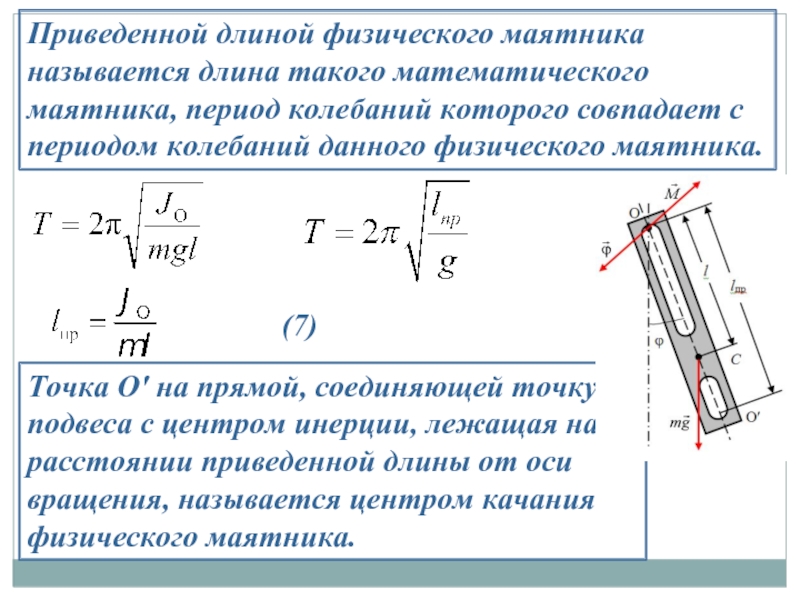
Слайд 8Приведенной длиной физического маятника называется длина такого математического маятника, период колебаний
Точка О′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника.
(7)
Слайд 92 учебный вопрос: Свободные затухающие колебания
r − коэффициент сопротивления среды
Уравнение
⇒
⇒
⇒
ДУ затухающих колебаний
(8)
Слайд 10β - коэф.затухания; ω0 - частота собственных колебаний без трения.
-
Решение:
(9)
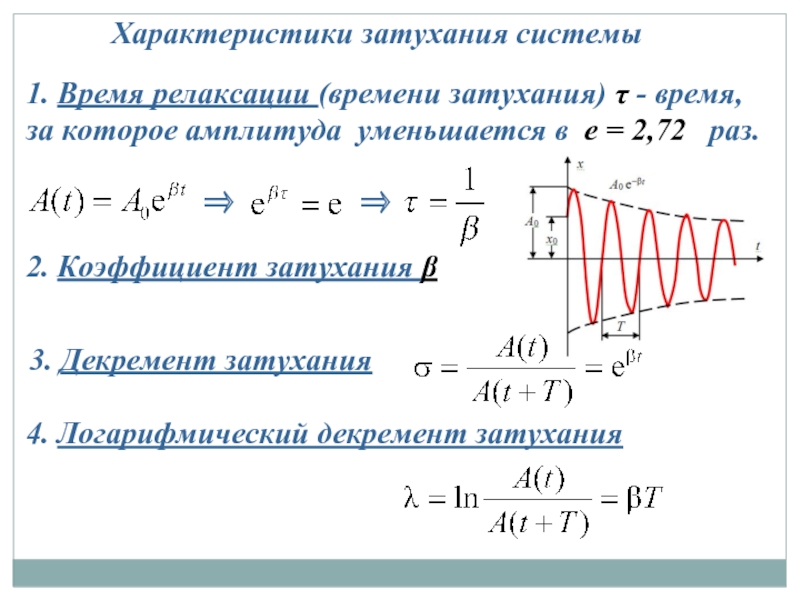
Слайд 11Характеристики затухания системы
2. Коэффициент затухания β
1. Время релаксации (времени затухания) τ
⇒
3. Декремент затухания
4. Логарифмический декремент затухания
⇒
Слайд 125. Добротность колебательной системы - число полных колебаний, совершаемых системой за
Энергетический смысл добротности:
Добротность характеризует относительную убыль энергии колебательной системы из-за наличия трения на интервале времени, равном одному периоду колебаний.
Слайд 143 учебный вопрос: Вынужденные колебания. Резонанс.
Пусть колебательная система подвергается действию внешней
Второй закон Ньютона:
(10)