- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Дифракция. (Тема 31) презентация
Содержание
- 1. Дифракция. (Тема 31)
- 2. 1. ОПРЕДЕЛЕНИЕ ДИФРАКЦИИ Дифракцией называется круг явлений,
- 3. 2. ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ Между и интерференцией
- 4. 3. ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ Проникновение световых волн
- 5. 4. ИНТЕГРАЛ ФРЕНЕЛЯ Согласно принципу Гюйгенса-Френеля каждый
- 6. 5. ЗОНЫ ФРЕНЕЛЯ Вычисление интеграла Френеля является
- 7. 6. ВКЛАД ОТ СОСЕДНИХ ЗОН Рассмотрим вклад
- 8. 7. ПЛОЩАДИ ЗОН ФРЕНЕЛЯ (I) Внешняя
- 9. 7. ПЛОЩАДИ ЗОН ФРЕНЕЛЯ (II) Воспользуемся
- 10. 7. ПЛОЩАДИ ЗОН ФРЕНЕЛЯ (III) Площадь сферического
- 11. 8. РАДИУСЫ ЗОН ФРЕНЕЛЯ По теореме
- 12. 9. АМПЛИТУДА КОЛЕБАНИЙ ДЛЯ ЗОН ФРЕНЕЛЯ
- 13. 10. ПОЛНОСТЬЮ ОТКРЫТАЯ ВОЛНОВАЯ ПОВЕРХНОСТЬ Фазы
- 14. 11. МЕТОД ГРАФИЧЕСКОГО СЛОЖЕНИЯ АМПЛИТУД Разобьем волновую
- 15. 12. ХАРАКТЕРНЫЕ СЛУЧАИ
- 16. 13. ЗОННАЯ ПЛАСТИНКА Колебания от четных и
- 17. 14. ДИФРАКЦИЯ ФРЕНЕЛЯ И ДИФРАКЦИЯ ФРАУНГОФЕРА Различают
- 18. 15. ДИФРАКЦИЯ ФРЕНЕЛЯ ОТ КРУГЛОГО ОТВЕРСТИЯ Поставим
- 19. 16. МАКСИМУМЫ/МИНИМУМЫ ДЛЯ КРУГЛОГО ОТВЕРСТИЯ Суммарная амплитуда
- 20. 17. ДИАФРАГМА
- 21. 18. ДИФРАКЦИЯ ОТ КРУГЛОГО ДИСКА Поместим между
- 22. 19. ПЯТНО ПУАССОНА
- 23. 20. КРАЙ ПОЛУПЛОСКОСТИ Поместим на пути плосской
- 24. 21. ЗОНЫ ШУСТЕРА Разобьем открытую часть
- 25. 22. ВЕКТОРНАЯ ДИАГРАММА ДЛЯ ПОЛУПЛОСКОСТИ Из соотношений
- 26. 23. СПИРАЛЬ КОРНЮ (I) Если ширину зон
- 27. 23. СПИРАЛЬ КОРНЮ (II) Найдем производную кривой,
- 28. 23. СПИРАЛЬ КОРНЮ (III) Установим связь
- 29. 24. РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ
- 30. 25. ДИФРАКЦИЯ ФРЕНЕЛЯ ОТ ЩЕЛИ Бесконечно длинную
- 31. 26. ЩЕЛЬ ПЕРЕМЕННОЙ ШИРИНЫ Если изменять ширину
- 32. 27. ШИРОКАЯ ЩЕЛЬ При большой ширине щели
- 33. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (I)
- 34. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (II)
- 35. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (III)
- 36. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ
- 37. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (V)
- 38. 28. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (VI) Результат
- 39. 29. ДИФРАКЦИЯ ОТ ЩЕЛИ. МАКСИМУМЫ И МИНИМУМЫ
- 40. 30. МАКСИМУМЫ И МИНИМУМЫ. ЗОННЫЙ ПОДХОД Условие
- 41. 31. РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ (I) Интенсивность света
- 42. 31. РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ (II) Краям центрального
- 43. 32. ДИФРАКЦИОННАЯ РЕШЕТКА (I) Дифракционной решеткой
- 44. 32. ДИФРАКЦИОННАЯ РЕШЕТКА (II) Каждая из
- 45. 32. ДИФРАКЦИОННАЯ РЕШЕТКА (III) Пусть радиус
- 46. 33. ДИФРАКЦИОННАЯ РЕШЕТКА. МАКСИМУМЫ И МИНИМУМЫ (I)
- 47. 33. ДИФРАКЦИОННАЯ РЕШЕТКА. МАКСИМУМЫ И МИНИМУМЫ (II)
- 48. 34. ДИФРАКЦИОННАЯ РЕШЕТКА КАК СПЕКТРАЛЬНЫЙ ПРИБОР Положение
Слайд 21. ОПРЕДЕЛЕНИЕ ДИФРАКЦИИ
Дифракцией называется круг
явлений, наблюдаемых при
распространении света в среде
с резкими
связанных с отклонением от
законов геометрической
оптики.
Дифракция приводит к огибанию волнами
препятствий и проникновению света в
область геометрической тени.
Для наблюдения дифракции световых волн
необходимо создание специальных условий.
Это обусловлено малостью длины световой
волны.
Слайд 32. ДИФРАКЦИЯ И
ИНТЕРФЕРЕНЦИЯ
Между и интерференцией и дифракцией нет существенного физического
различия.
светового
Перераспределение интенсивности, возникающее в результате
наложения волн, возбуждаемых конечным числом источников,
принято называть интерференцией.
В случае суперпозиции волн от источников, расположенных непрерывно,
принято говорить о дифракции света.
Оба явления заключаются в перераспределении
Слайд 43. ПРИНЦИП
ГЮЙГЕНСА-ФРЕНЕЛЯ
Проникновение световых волн в область
геометрической тени может быть объяснено
с
до которой доходит волновой фронт,
cлужит источником вторичных сферических волн;
огибающая этих волн дает положение
фронта волны в следующие моменты времени.
Однако, этот принцип не дает сведений
об амплитуде и об интенсивности
вторичных волн,
в различных направлениях.
Учет амплитуд и фаз вторичных волн
позволяет найти амплитуду суммарной
волны в любой точке пространства.
Развитый таким способом
принцип Гюйгенса получил название
принципа Гюйгенса-Френеля.
каждая точка,
распространяющихся
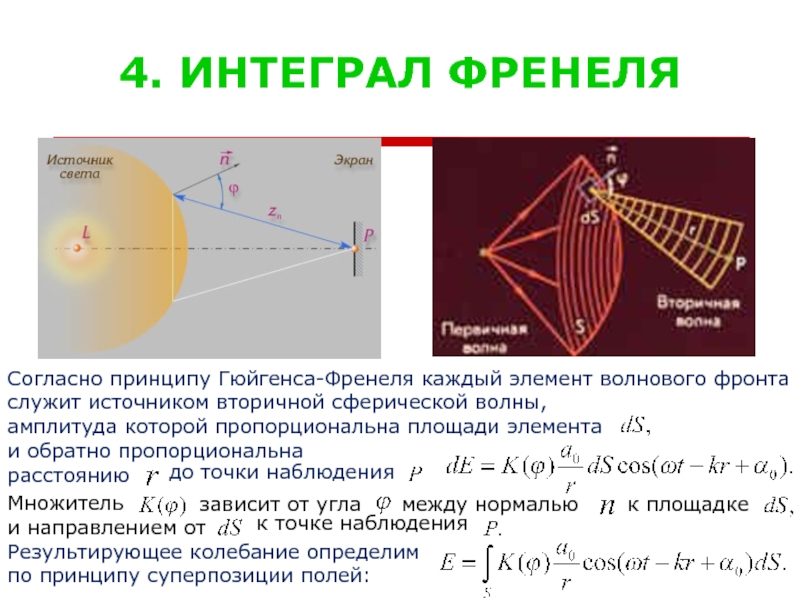
Слайд 54. ИНТЕГРАЛ ФРЕНЕЛЯ
Согласно принципу Гюйгенса-Френеля каждый элемент волнового фронта
служит источником вторичной
амплитуда которой пропорциональна площади элемента
и обратно пропорциональна
расстоянию
Множитель
и направлением от
Результирующее колебание определим
по принципу суперпозиции полей:
до точки наблюдения
к площадке
между нормалью
зависит от угла
к точке наблюдения
Слайд 65. ЗОНЫ ФРЕНЕЛЯ
Вычисление интеграла Френеля
является весьма трудоемкой задачей.
Однако, если источники расположены
достаточной симметрией, амплитуда
результирующего поля может быть
найдена простым алгебраическим или
геометрическим суммированием.
Для нахождения амплитуды колебаний
в точке наблюдения
кольцевые зоны волновую поверхность
так,
зоны до точки наблюдения отличаются
на
Френеля.
симметричны относительно линии LP.
разобьем на
что расстояния от краев каждой
Эти зоны называются зонами
Очевидно, что зоны Френеля
Слайд 76. ВКЛАД ОТ
СОСЕДНИХ ЗОН
Рассмотрим вклад в
результирующее волновое
поле от аналогичных
точек двух
то есть лежащих симметрично
относительно границ зон -
в их серединах или у внешних,
или у внутренних краев.
Поскольку расстояния от
краев каждой зоны до точки
наблюдения отличаются на
то волны, приходящие
от аналогичных точек будут
колебаться в противофазе.
Это означает, что и результирующие колебания, создаваемые каждой из
зон в целом, будут для соседних зон различаться на
колебания в точке наблюдения от соседних зон ослабляют друг друга.
Следовательно,
Слайд 87. ПЛОЩАДИ
ЗОН ФРЕНЕЛЯ (I)
Внешняя граница k-ой зоны
выделяет на волновой поверхности
сферический
Обозначим площадь этого
сегмента через
площадь k-ой зоны Френеля
можно представить в виде
где
выделяемого внешней
границей (k-1)-зоны.
Из рисунка видно, что
Здесь:
k-ой зоны.
Тогда
– площадь сегмента,
– радиус внешней границы
– радиус волновой поверхности;
Возведя скобки в квадрат, получим
Слайд 97. ПЛОЩАДИ
ЗОН ФРЕНЕЛЯ (II)
Воспользуемся этим «двойным уравнением» для нахождения
Ограничившись
малости
содержащим
можно ввиду
пренебречь слагаемым,
В этом приближении
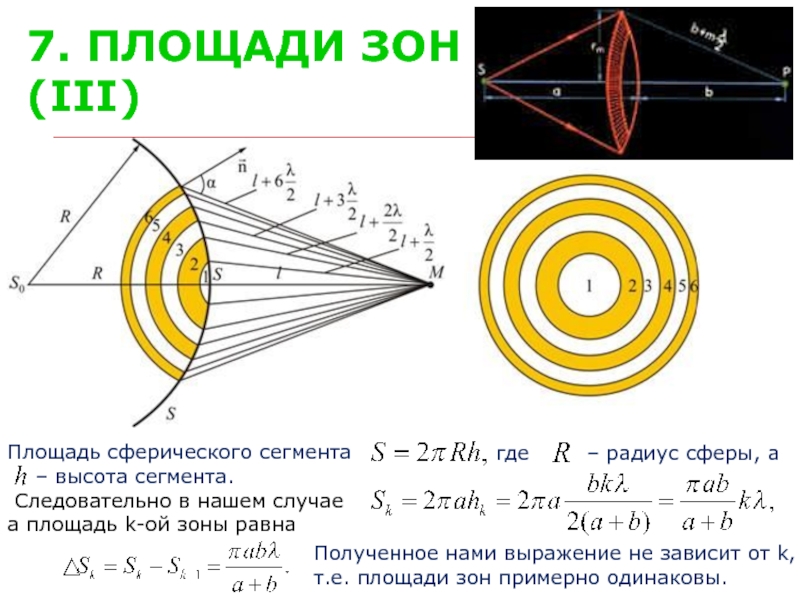
Слайд 107. ПЛОЩАДИ ЗОН ФРЕНЕЛЯ (III)
Площадь сферического сегмента
– высота сегмента.
Следовательно в нашем случае
а площадь k-ой зоны равна
Полученное нами выражение не зависит от k,
т.е. площади зон примерно одинаковы.
– радиус сферы, а
где
Слайд 118. РАДИУСЫ
ЗОН ФРЕНЕЛЯ
По теореме Пифагора
При не слишком больших k высота
сегмента
поэтому можно считать, что
Если предположить, что
то для радиуса первой (центральной)
зоны получается значение
Радиусы последующих зон пропорциональна
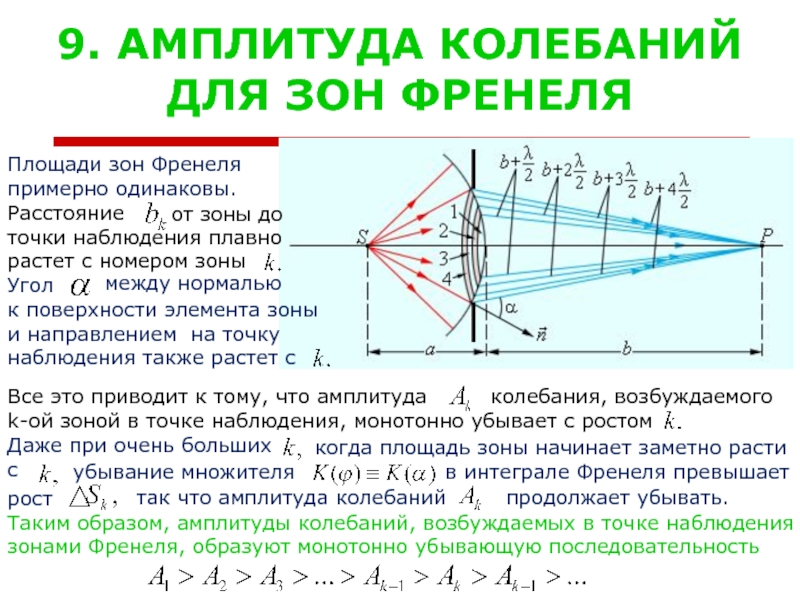
Слайд 129. АМПЛИТУДА КОЛЕБАНИЙ
ДЛЯ ЗОН ФРЕНЕЛЯ
Площади зон Френеля
примерно одинаковы.
Расстояние
точки наблюдения
растет с номером зоны
Угол
к поверхности элемента зоны
и направлением на точку
наблюдения также растет с
Все это приводит к тому, что амплитуда
k-ой зоной в точке наблюдения, монотонно убывает с ростом
Даже при очень больших
с
рост
Таким образом, амплитуды колебаний, возбуждаемых в точке наблюдения
зонами Френеля, образуют монотонно убывающую последовательность
от зоны до
между нормалью
колебания, возбуждаемого
когда площадь зоны начинает заметно расти
в интеграле Френеля превышает
убывание множителя
продолжает убывать.
так что амплитуда колебаний
Слайд 1310. ПОЛНОСТЬЮ ОТКРЫТАЯ
ВОЛНОВАЯ ПОВЕРХНОСТЬ
Фазы колебаний, от соседних
зон Френеля отличаются на
Поэтому
результирующего колебания
будет справедливо выражение
Четные и нечетные амплитуды
противоположны по знаку.
Представим выражение для результирующей амплитуды в виде
Вследствие монотонности убывания амплитуды с ростом номера зоны
можно приближенно считать, что
Полученный результат означает,
что амплитуда, создаваемая в точке наблюдения всей сферической
волновой поверхностью, равна половине амплитуды, создаваемой лишь
одной центральной зоной Френеля.
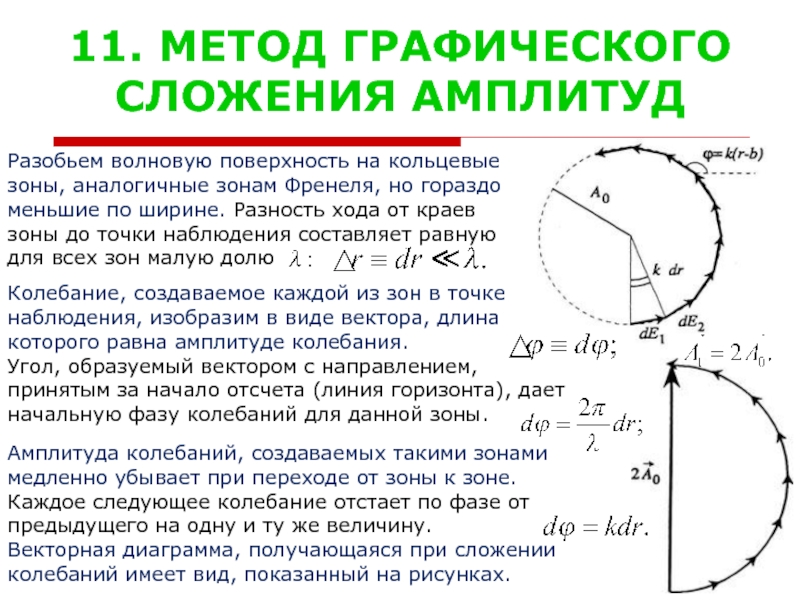
Слайд 1411. МЕТОД ГРАФИЧЕСКОГО
СЛОЖЕНИЯ АМПЛИТУД
Разобьем волновую поверхность на кольцевые
зоны, аналогичные зонам Френеля,
меньшие по ширине. Разность хода от краев
зоны до точки наблюдения составляет равную
для всех зон малую долю
Колебание, создаваемое каждой из зон в точке
наблюдения, изобразим в виде вектора, длина
которого равна амплитуде колебания.
Угол, образуемый вектором с направлением,
принятым за начало отсчета (линия горизонта), дает
начальную фазу колебаний для данной зоны.
Амплитуда колебаний, создаваемых такими зонами
медленно убывает при переходе от зоны к зоне.
Каждое следующее колебание отстает по фазе от
предыдущего на одну и ту же величину.
Векторная диаграмма, получающаяся при сложении
колебаний имеет вид, показанный на рисунках.
Слайд 1613. ЗОННАЯ
ПЛАСТИНКА
Колебания от четных и нечетных зон
Френеля находятся в противофазе и,
следовательно,
друга.
Если поставить на пути световой волны
пластинку, которая перекрывала бы все
нечетные (а) или четные (b) зоны, то
интенсивность света резко вырастет.
Такая пластинка, называемая зонной,
действует как собирающая линза.
Еще большего эффекта можно достичь, если
не перекрывать четные (или нечетные) зоны,
а изменить фазу их колебаний на
Это можно осуществить с помощью прозрачной
пластинки, толщина которой в местах четных (с)
или нечетных (1) зон изменена надлежащим
образом.
Такая пластинка называется фазовой зонной
пластинкой или линзой Френеля.
Слайд 1714. ДИФРАКЦИЯ ФРЕНЕЛЯ И
ДИФРАКЦИЯ ФРАУНГОФЕРА
Различают два вида дифракции. Если
источник света
расположены друг от друга настолько
далеко, что световые лучи можно
считать параллельными, то говорят о
дифракции Фраунгофера. Если лучи
нельзя считать параллельными, то
говорят о дифракции Френеля.
Жан Огюстен Френель
1788 – 1827
французский физик
Йозеф Фраунгофер
1787 – 1826
немецкий физик
Слайд 1815. ДИФРАКЦИЯ ФРЕНЕЛЯ
ОТ КРУГЛОГО ОТВЕРСТИЯ
Поставим на пути сферической световой волны непрозрачную
что выполняется следующее соотношение
Это означает, что отверстие (диафрагма) оставит на преграде открытыми
ровно
Френеля.
(от источника до
Пусть расстояние
(от преграды до экрана) таковы,
первых зон
Причем,
Слайд 1916. МАКСИМУМЫ/МИНИМУМЫ
ДЛЯ КРУГЛОГО ОТВЕРСТИЯ
Суммарная амплитуда в центре дифракционной картины будет равна
Перед
Если
максимум,
Для четного числа зон амплитуда
результирующего колебания будет
Объединяя оба выражения получим:
– нечетное, и минус – если четное.
берется знак плюс, если
– нечетное то в центре будет наблюдаться
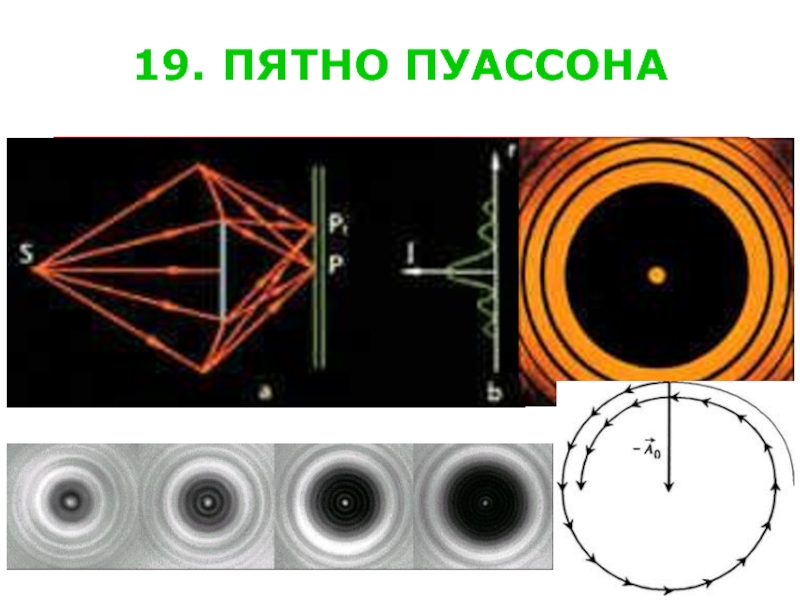
Слайд 2118. ДИФРАКЦИЯ ОТ
КРУГЛОГО ДИСКА
Поместим между источником света
и точкой наблюдения преграду в
виде непрозрачного диска малого
радиуса.
первых зон, то амплитуда будет
Полученный результат означает, что в центре геометрической тени будет
светлое пятно, получившее название пятна Пуассона.
наблюдению впервые выполнил Доминик Франсуа Араго в 1818 году.
Если диск закроет
Опыт по его
Слайд 2320. КРАЙ ПОЛУПЛОСКОСТИ
Поместим на пути плосской световой волны препятствие
в виде
волновых поверхностей.
экран, на котором будем наблюдать дифракционную картину.
Расположим эту полуплоскость так, чтобы она совпала с одной из
За полуплоскостью параллельно ей расположим
Слайд 2421. ЗОНЫ
ШУСТЕРА
Разобьем открытую часть волновой
поверхности на зоны, имеющие вид очень
Ширину зон выберем так, чтобы
расстояния от точки наблюдения
до краев любой зоны отличались
(в плоскости рисунка) на одну и
ту же величину
Тогда колебания, создаваемые
в точке наблюдения соседними
зонами, будут отличаться по
фазе на одну и туже величину.
Чтобы установить зависимость амплитуды от номера зоны
площади зон.
Положив в этой формуле
Ширины и площади зон находятся между собой в соотношении:
зон
Из рисунка ясно, что суммарная ширина первых
оценим
Следовательно
получим, что
Слайд 2522. ВЕКТОРНАЯ ДИАГРАММА
ДЛЯ ПОЛУПЛОСКОСТИ
Из соотношений между площадями зон Шустера
вытекает, что амплитуда
создаваемых в точке наблюдения отдельными
зонами,
очень быстро, затем это убывание становится
медленным.
Поэтому ломанная линия,
получающаяся при
графическом сложении
амплитуд колебаний, возбуждаемых зонами Шустера,
идет сначала более полого, чем в случае кольцевых
зон,
при аналогичном
построении примерно
равны.
1-ый квадрант – правые зоны;
3-ий квадрант – левые зоны.
вначале (для первых зон) убывает
площади которых
Слайд 2623. СПИРАЛЬ КОРНЮ (I)
Если ширину зон устремить к нулю,
ломанная линия превратится
плавную кривую, называемую
спиралью Корню (клотоида).
Уравнение спирали Корню в
параметрической форме имеет вид
Эти интегралы называются
интегралами Френеля.
берутся в элементарных функциях.
Смысл параметра
даёт длину дуги кривой Корню, отсчитанной от начала координат.
Точки
называются фокусами или полюсами спирали Корню.
Они не
заключается в том, что
к которым асимптотически приближается спираль при
и
Слайд 2723. СПИРАЛЬ КОРНЮ (II)
Найдем производную
кривой, отвечающей данному значению
параметра
Из интегралов
при приращении длины
координаты
получат приращение
Следовательно
Если
к спирали Корню в данной точке,
смысла производной можем составить уравнение
Это означает, что в точке, отвечающей длине
кривой, например к оси Если
в точке
на
и
– угол наклона касательной
то на основании геометрического
касательная к спирали Корню перпендикулярна
и так далее.
то
если
то
Слайд 2823. СПИРАЛЬ
КОРНЮ (III)
Установим связь между значением
параметра
геометрической тени, и координатой
от края тени.
Для спирали Корню
Угол наклона касательной к спирали
Корню
колебаний волн,
волновой поверхности, лежащими
против точки наблюдения
равна )
Поэтому угол
лучей
отвечающим краю
совпадает со сдвигом фаз
испущенных точками
(координата
и на границе тени
можно выразить через оптическую разность хода этих
Слайд 3025. ДИФРАКЦИЯ
ФРЕНЕЛЯ ОТ ЩЕЛИ
Бесконечно длинную щель можно образовать,
расположив рядом две обращенные
стороны полуплоскости.
Для точки
начало и конец результирующего вектора
находятся в симметричных относительно
начала координат точках спирали Корню.
Если сместиться в точку
края щели, начало результирующего вектора
переместится в нулевую точку спирали.
вектора переместится по спирали к ее полюсу.
При углублении в область геометрической
тени начало и конец результирующего вектора
будут скользить по спирали и в конце концов
окажутся на наименьшем расстоянии друг от
друга
начало и конец вектора отойдут друг от друга – интенсивность растет.
лежащей против середины щели,
лежащую против
Конец
В дальнейшем
– наблюдается минимум интенсивности.
(точка )
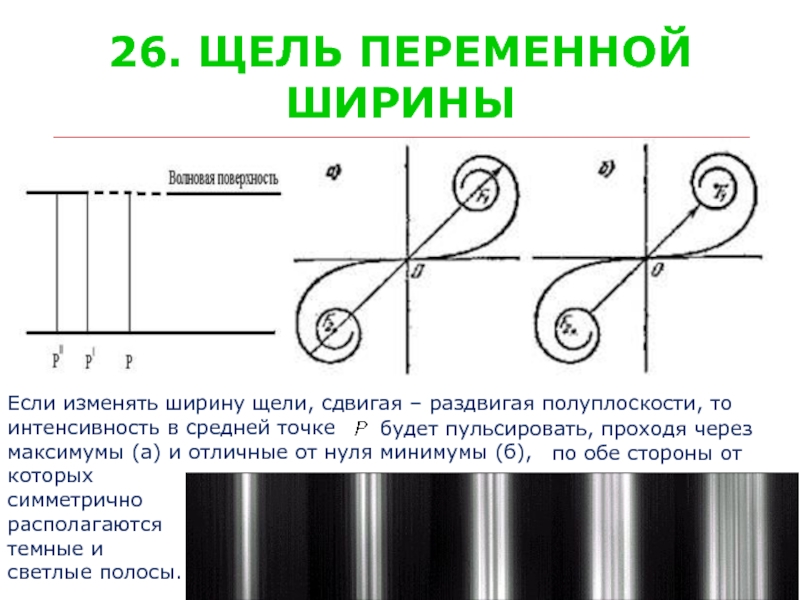
Слайд 3126. ЩЕЛЬ ПЕРЕМЕННОЙ
ШИРИНЫ
Если изменять ширину щели, сдвигая – раздвигая полуплоскости, то
интенсивность
максимумы (а) и отличные от нуля минимумы (б),
которых
симметрично
располагаются
темные и
светлые полосы.
будет пульсировать, проходя через
по обе стороны от
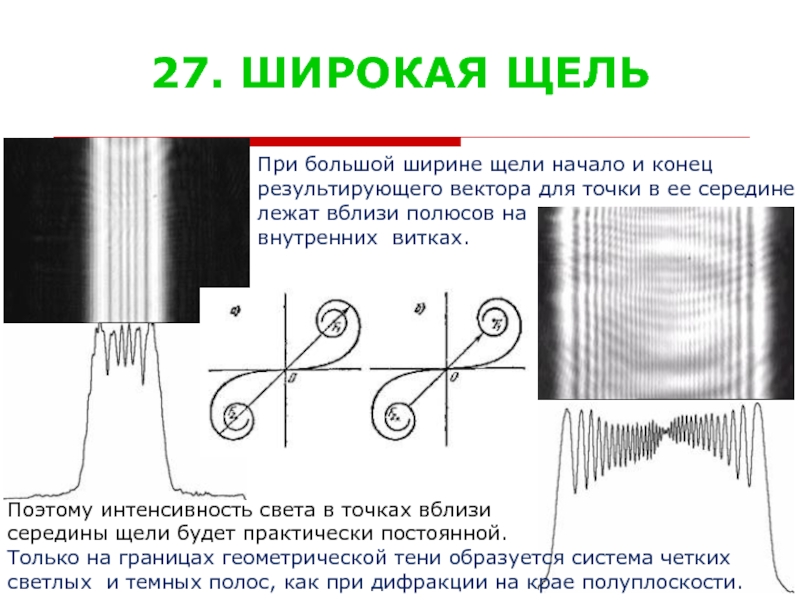
Слайд 3227. ШИРОКАЯ ЩЕЛЬ
При большой ширине щели начало и конец
результирующего вектора для
лежат вблизи полюсов на
внутренних витках.
Поэтому интенсивность света в точках вблизи
середины щели будет практически постоянной.
Только на границах геометрической тени образуется система четких
светлых и темных полос, как при дифракции на крае полуплоскости.
Слайд 3328. ДИФРАКЦИЯ
ФРАУНГОФЕРА ОТ ЩЕЛИ (I)
Пусть на длинную щель (длина много
ширины щели) перпендикулярно к ней падает
плоская световая волна.
Поместим за щелью собирающую линзу, а в ее
фокальной плоскости экран. Плоскости щели,
линзы и экрана параллельны друг другу.
Разобьем открытую часть волновой поверхности
на параллельные краям щели элементарные
прямоугольные зоны шириной
Вторичные волны, посылаемые зонами под углом
к оптической оси системы, соберутся на
экране в определенной точке
Каждая элементарная зона создает в точке
свой вклад в результирующее колебание
Слайд 3428. ДИФРАКЦИЯ
ФРАУНГОФЕРА ОТ ЩЕЛИ (II)
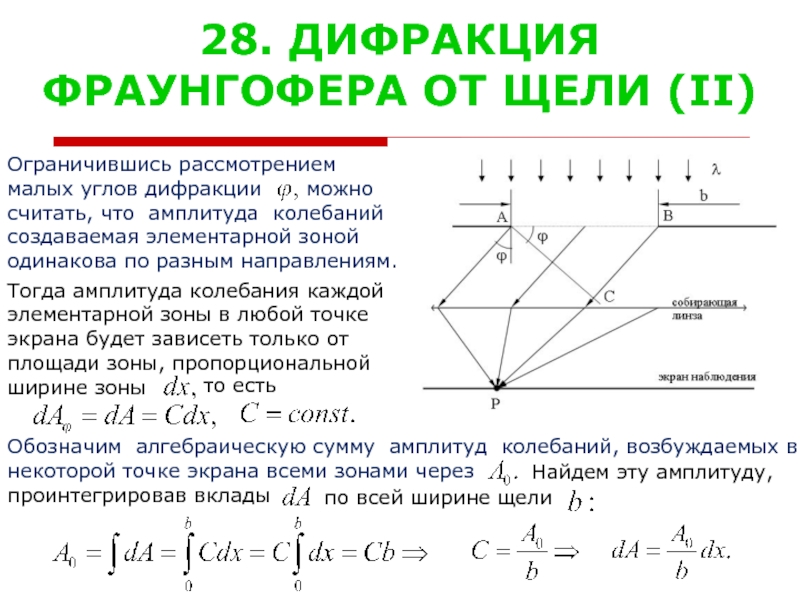
Ограничившись рассмотрением
малых углов дифракции
считать, что амплитуда
создаваемая элементарной зоной
одинакова по разным направлениям.
Тогда амплитуда колебания каждой
элементарной зоны в любой точке
экрана будет зависеть только от
площади зоны, пропорциональной
ширине зоны
Обозначим алгебраическую сумму амплитуд колебаний, возбуждаемых в
некоторой точке экрана всеми зонами через
проинтегрировав вклады
можно
то есть
Найдем эту амплитуду,
по всей ширине щели
Слайд 3528. ДИФРАКЦИЯ
ФРАУНГОФЕРА ОТ ЩЕЛИ (III)
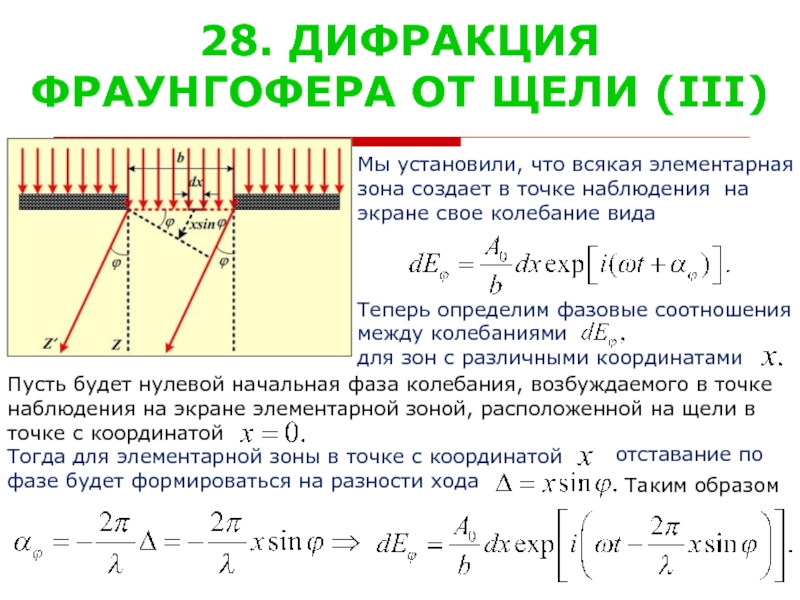
Мы установили, что всякая элементарная
зона создает
экране свое колебание вида
Теперь определим фазовые соотношения
между колебаниями
для зон с различными координатами
Пусть будет нулевой начальная фаза колебания, возбуждаемого в точке
наблюдения на экране элементарной зоной, расположенной на щели в
точке с координатой
Тогда для элементарной зоны в точке с координатой
фазе будет формироваться на разности хода
Таким образом
отставание по
Слайд 3628. ДИФРАКЦИЯ ФРАУНГОФЕРА ОТ ЩЕЛИ (IV)
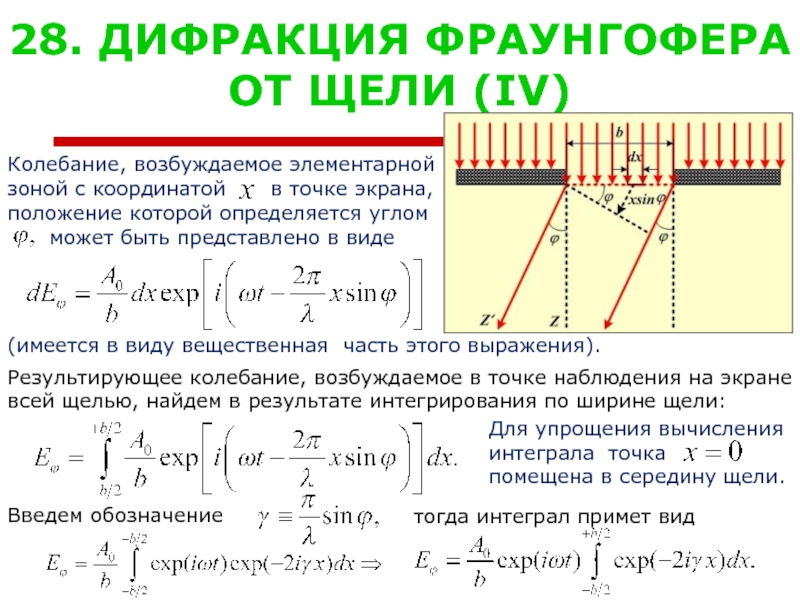
Колебание, возбуждаемое элементарной
зоной
положение которой определяется углом
может быть представлено в виде
(имеется в виду вещественная часть этого выражения).
Результирующее колебание, возбуждаемое в точке наблюдения на экране
всей щелью, найдем в результате интегрирования по ширине щели:
Для упрощения вычисления
интеграла точка
помещена в середину щели.
Введем обозначение
в точке экрана,
тогда интеграл примет вид
Слайд 3728. ДИФРАКЦИЯ
ФРАУНГОФЕРА ОТ ЩЕЛИ (V)
Для результирующего колебания,
создаваемого волнами идущими от
под углом
получено интегральное выражение
В результате вычисления получим:
к оптической оси системы,
Слайд 3828. ДИФРАКЦИЯ
ФРАУНГОФЕРА ОТ ЩЕЛИ (VI)
Результат сложения всех волн, идущих от
щели в
Выражение в фигурных скобках задает
комплексную амплитуду
cуммарного колебания.
Воспользуемся формулой Эйлера:
После преобразования по формуле Эйлера выражение для комплексной
амплитуды примет вид
Слайд 3929. ДИФРАКЦИЯ ОТ ЩЕЛИ.
МАКСИМУМЫ И МИНИМУМЫ
Выражение для комплексной амплитуды
является вещественным.
определяет
колебания для волн,
под углом к оптической оси системы
Для точки, лежащей против центра линзы,
Подстановка этого значения в формулу
для амплитуды приводит к значению
Этот результат легко объяснить.
зон приходят в точку наблюдения
амплитуда результирующего колебания равна алгебраической сумме
амплитуд складываемых колебаний от всех элементарных зон.
При значениях угла
амплитуда
Его модуль
идущих от щели
колебания от элементарных
При
Следовательно
в одинаковой фазе.
удовлетворяющих условию
обращается в нуль.
Слайд 4030. МАКСИМУМЫ И МИНИМУМЫ.
ЗОННЫЙ ПОДХОД
Условие минимумов для дифракции Фраунгофера
на щели легко
Если разность хода от краев щели
то волновую поверхность, открываемую щелью,
можно разбить на
причем разность хода от краев каждой зоны
будет равна
соседних зон взаимно погашают друг друга,
так что результирующая амплитуда равна нулю.
Если разность
хода от краев
щели будет
число зон
будет
нечетным,
действие одной из них окажется
некомпенсированным и наблюдается максимум интенсивности.
равных по ширине зон,
Колебания от каждой пары
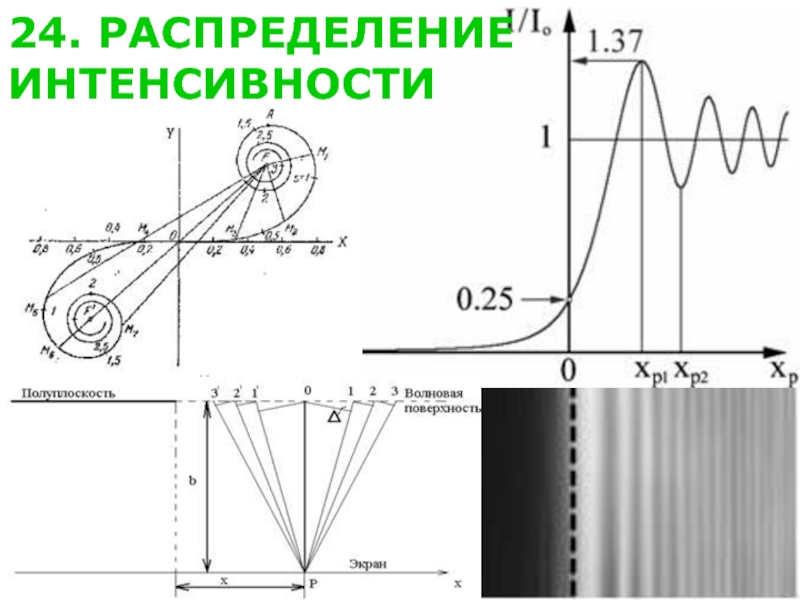
Слайд 4131. РАСПРЕДЕЛЕНИЕ
ИНТЕНСИВНОСТИ (I)
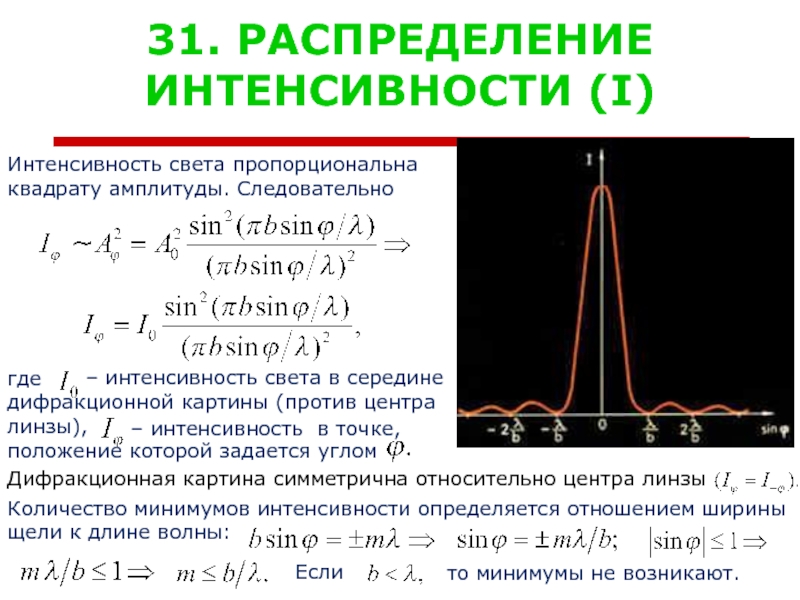
Интенсивность света пропорциональна
квадрату амплитуды. Следовательно
где
дифракционной картины (против
линзы),
положение которой задается углом
Дифракционная картина симметрична относительно центра линзы
Количество минимумов интенсивности определяется отношением ширины
щели к длине волны:
Если
– интенсивность света в середине
– интенсивность в точке,
то минимумы не возникают.
Слайд 4231. РАСПРЕДЕЛЕНИЕ
ИНТЕНСИВНОСТИ (II)
Краям центрального максимума соответствуют
значения угла
Следовательно, угловая ширина центрального
максимума
В случае, когда
минимумы не возникают – интенсивность убывает от середины к краям.
получающиеся из условия
то
Если
Слайд 4332. ДИФРАКЦИОННАЯ
РЕШЕТКА (I)
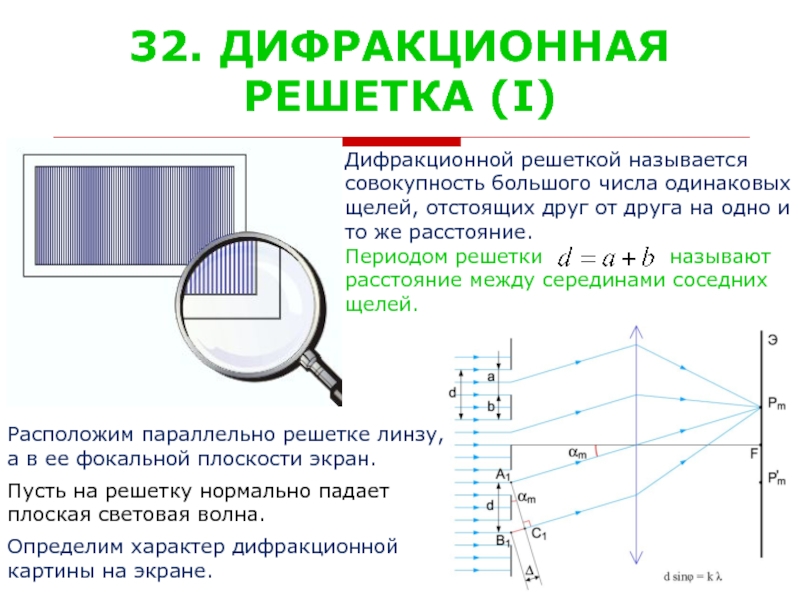
Дифракционной решеткой называется
совокупность большого числа одинаковых
щелей, отстоящих
то же расстояние.
Периодом решетки называют
расстояние между серединами соседних
щелей.
Расположим параллельно решетке линзу,
а в ее фокальной плоскости экран.
Пусть на решетку нормально падает
плоская световая волна.
Определим характер дифракционной
картины на экране.
Слайд 4432. ДИФРАКЦИОННАЯ
РЕШЕТКА (II)
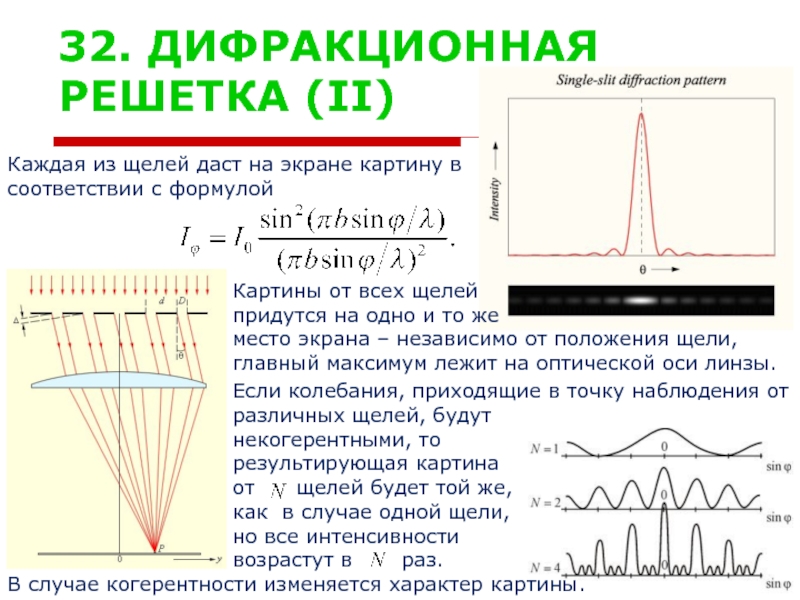
Каждая из щелей даст на экране картину в
соответствии
Картины от всех щелей
придутся на одно и то же
место экрана – независимо от положения щели,
главный максимум лежит на оптической оси линзы.
Если колебания, приходящие в точку наблюдения от
различных щелей, будут
некогерентными, то
результирующая картина
от щелей будет той же,
как в случае одной щели,
но все интенсивности
возрастут в раз.
В случае когерентности изменяется характер картины.
Слайд 4532. ДИФРАКЦИОННАЯ
РЕШЕТКА (III)
Пусть радиус когерентности
падающей волны превышает
длину решетки – колебания
щелей будут когерентными.
Результирующее колебание в
точке наблюдения будет
суммой колебаний с
одинаковой амплитудой
сдвинутых относительно друг
друга по фазе на одну и ту же
величину
В этих условиях результирующая амплитуда и интенсивность будут равны:
Из рисунка видно, что разность хода от соседних щелей
Следовательно, разность фаз для волн, идущих от соседних щелей будет
– интенсивность света, создаваемая одной щелью против центра линзы.
Слайд 4633. ДИФРАКЦИОННАЯ РЕШЕТКА.
МАКСИМУМЫ И МИНИМУМЫ (I)
Первый множитель обращается в нуль
в точках,
В этих точках интенсивность от
каждой из щелей в отдельности,
равна нулю (главные минимумы).
Второй множитель принимает значение
В этих направлениях колебания всех щелей совершаются в одной фазе,
амплитуда колебаний
В промежутках между соседними главными максимумами имеется
добавочных минимумов в направлениях, для которых колебания от щелей
взаимно погашают друг друга:
в точках, для которых
(главные максимумы).
Слайд 4733. ДИФРАКЦИОННАЯ РЕШЕТКА.
МАКСИМУМЫ И МИНИМУМЫ (II)
Главные минимумы:
Главные максимумы:
Добавочные минимумы:
Порядок наблюдающегося главного
углом дифракции, периодом решетки и длиной волны соотношением
Модуль синуса не может превысить единицы, поэтому
количество наблюдающихся главных максимумов
Угловая ширина центрального (нулевого) максимума будет зависеть от
положения ближайших к нему дополнительных минимумов, то есть
Слайд 4834. ДИФРАКЦИОННАЯ РЕШЕТКА
КАК СПЕКТРАЛЬНЫЙ ПРИБОР
Положение главных максимумов зависит от
длины волны:
пропускании через
все максимумы, кроме центрального, будут
разложены в спектр.
спектра обращен к центру дифракционной
картины, а красный – наружу.
В центре лежит узкий нулевой максимум;
у него окрашены только края, так как ширина
центрального максимума
По обе стороны от центрального максимума
расположены два спектра 1-го порядка,
затем два спектра 2-го порядка и т. д.
Положение красного конца спектра порядка
Поэтому при
Фиолетовый фланг этого
зависит от
будет
и фиолетового порядка