Проектирование машин и механизмов является комплексной задачей, которая решается в три этапа:
1-й этап: установление кинематической схемы механизма, которая обеспечивает требуемый вид и закон движения;
2-й этап: разработка конструктивной схемы механизма, обеспечивающей его прочность, жёсткость, долговечность, требуемый КПД и др.;
3-й этап: разработка технологических технико-экономических показателей механизма, определяемых его эксплуатацией, ремонтом и обслуживанием.
В ТММ, в основном, решается задача первого этапа с учётом вопросов, связанных со вторым и третьим этапами. Задача синтеза кинематических схем механизмов многокритериальная, поскольку механизм должен удовлетворять различным геометрическим, кинематическим и динамическим условиям.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синтез механизмов. Основные задачи и методы синтеза презентация
Содержание
- 1. Синтез механизмов. Основные задачи и методы синтеза
- 2. Тема 6 Для
- 3. Тема 6 Задаются
- 4. Тема 6 В
- 5. Тема 6 Различают
- 6. Тема 6 Классификация простых зубчатых механизмов. По
- 7. Тема 6 2. По характеру расположения валов
- 8. Тема 6 3. По типу взаимоогибаемых кривых,
- 9. Тема 6
- 10. Тема 6
- 11. Тема 6
- 12. Тема 6
- 13. Тема 6
- 14. Тема 6
- 15. Тема 6 Основной теореме
- 16. Тема 6
- 17. Тема 6
- 18. Тема 6
- 19. Тема 6 Остальные
- 20. Тема 6
- 21. Тема 6
- 22. Тема 6
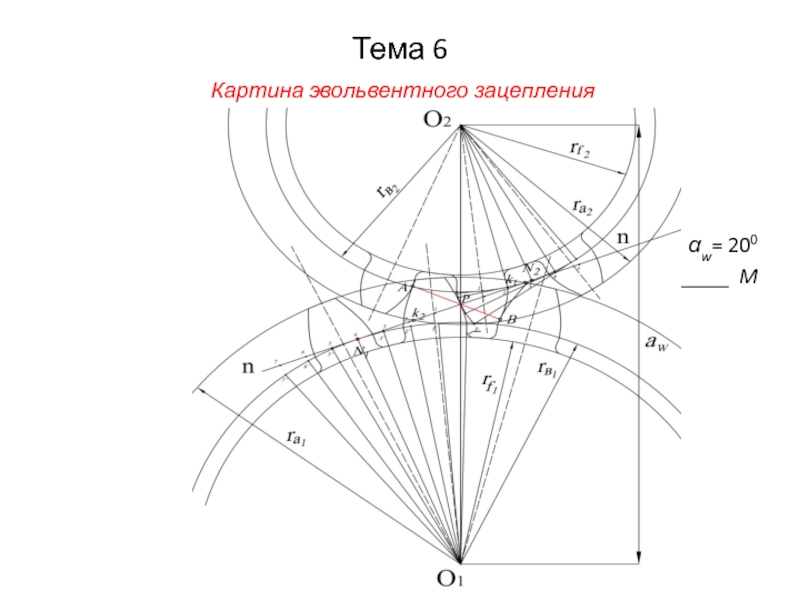
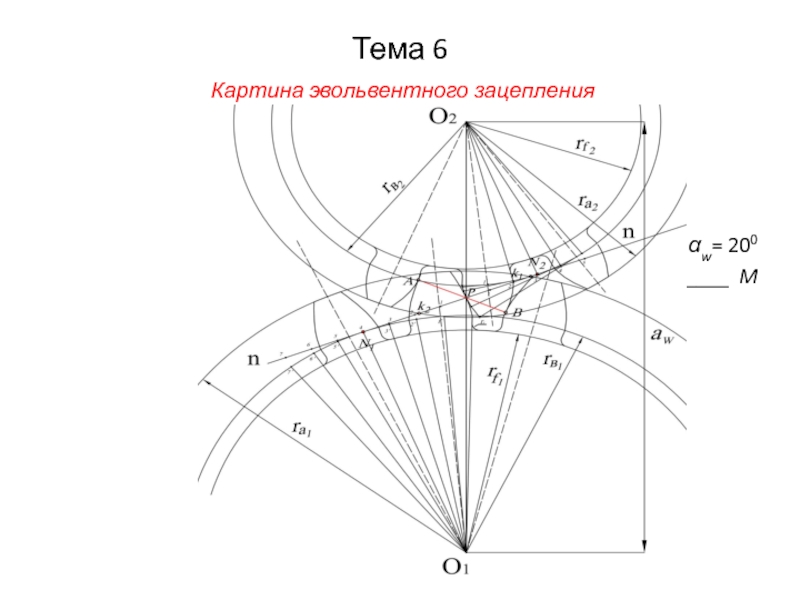
- 23. Тема 6 Картина эвольвентного зацепления αw= 200 ______ M
- 24. Тема 6
- 25. Тема 6 Картина эвольвентного зацепления αw= 200 ______ M
- 26. Тема 6 Построение эвольвенты зуба первого колеса
- 27. Тема 6 Построение эвольвенты зуба первого колеса
- 28. Тема 6 Построение эвольвенты зуба первого колеса (крупнее)
- 29. Тема 6
- 30. Тема 6 Построение эвольвенты зуба первого колеса (продолжение)
- 31. Тема 6 Построение эвольвенты первого колеса (продолжение)
- 32. Тема 6 Построение эвольвенты первого колеса (продолжение)
- 33. Тема 6
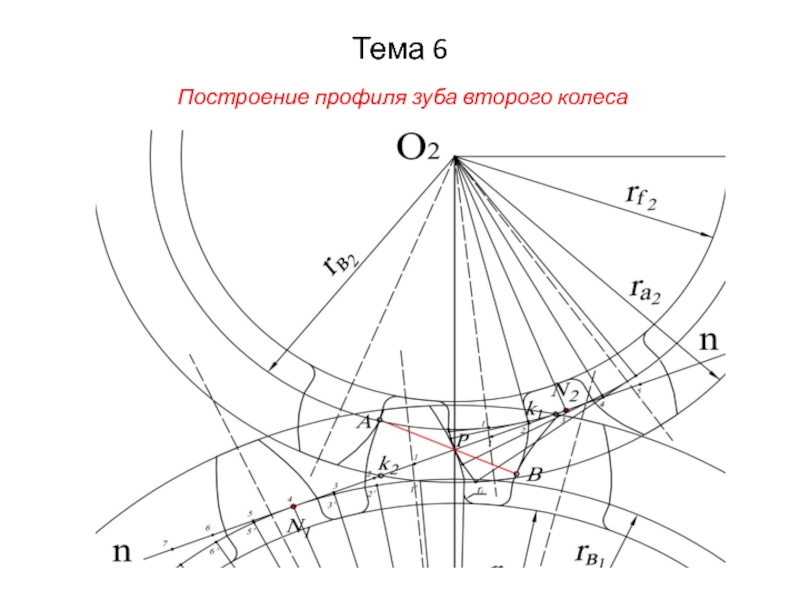
- 34. Тема 6 Построение профиля зуба второго колеса
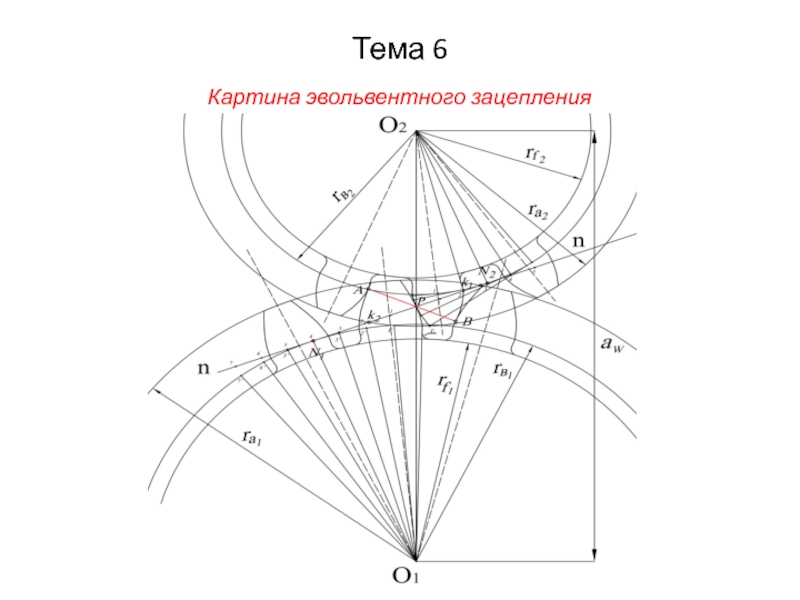
- 35. Тема 6 Картина эвольвентного зацепления
- 36. Тема 6 Преимущества эвольвентного зацепления: 1. Линия
- 37. Тема 6 6.2.6. Методы изготовления зубчатых колес
- 38. Тема 6 Наибольшее
- 39. Тема 6 Самым универсальным
- 40. Тема 6
- 41. Тема 6 Значения модуля зацепления
- 42. Тема 6
- 43. Тема 6 При этом,
- 44. Тема 6
- 45. Тема 6
- 46. Тема 6 Толщины
- 47. Тема 6 6.2.8. Определение угла зацепления
- 48. Тема 6 Зная угол
- 49. Тема 6 6.2.9. Определение радиусов окружностей впадин
- 50. Тема 6 6.2.10. Виды зацепления колес
- 51. Тема 6
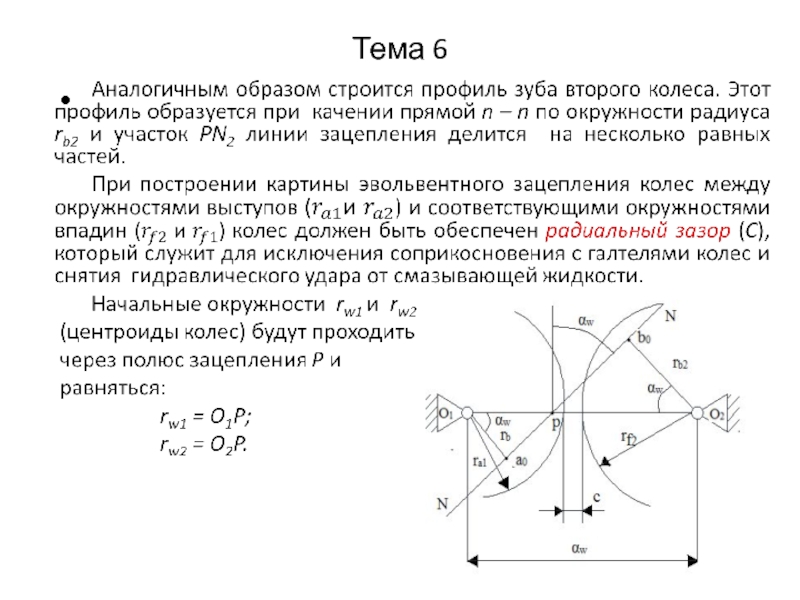
Слайд 2Тема 6
Для решения подобных задач используются различные
численные методы, основанные на применении ЭВМ: случайного поиска (метод Монте-Карло); направленного поиска; комбинированного поиска; наилучшего приближения функций (метод Чебышева П.Л.) и другие.
Задачи кинематического синтеза:
1.Преобразование вращательного движения вокруг одной оси во вращательное движение вокруг другой оси;
2.Преобразование вращательного движения вокруг одной оси в движение вдоль некоторой прямой и наоборот;
3.Преобразование поступательного движения вдоль одной прямой в поступательное движение вдоль другой прямой;
4.Воспроизведение одной из точек механизма заданной траектории.
Для решения первых трех задач задаются требуемые законы движения звеньев, а для решения четвертой задачи – траектория движения (аналитическим или графическим способами).
Задачи кинематического синтеза:
1.Преобразование вращательного движения вокруг одной оси во вращательное движение вокруг другой оси;
2.Преобразование вращательного движения вокруг одной оси в движение вдоль некоторой прямой и наоборот;
3.Преобразование поступательного движения вдоль одной прямой в поступательное движение вдоль другой прямой;
4.Воспроизведение одной из точек механизма заданной траектории.
Для решения первых трех задач задаются требуемые законы движения звеньев, а для решения четвертой задачи – траектория движения (аналитическим или графическим способами).
Слайд 3Тема 6
Задаются углы поворота выходного звена в
зависимости от угла поворота, длительность периода остановки выходного звена и т.д. Кроме того, указываются желаемые конструктивные формы механизмов и некоторые условия динамического характера, включающие к.п.д., устойчивость, прочность.
Перечисленные задачи синтеза наиболее просто и точно решаются с помощью механизмов, в состав которых наряду с низшими входят высшие КП. Эти механизмы позволяют: изменять скорости и законы движения звеньев и характер механического движения; осуществлять раздачу и суммирование движений; передавать движения между осями, произвольно расположенными в пространстве; осуществлять бесступенчатое изменение скорости движения.
К механизмам с высшими КП относятся зубчатые, кулачковые, фрикционные и волновые механизмы. К механизмам с низшими КП относятся рычажные, кулисные и синусные механизмы. Они более просты в изготовлении, но не обеспечивают высокой точности воспроизведения заданных законов движения. В дальнейшем будет рассмотрен синтез только плоских механизмов с высшими КП.
Перечисленные задачи синтеза наиболее просто и точно решаются с помощью механизмов, в состав которых наряду с низшими входят высшие КП. Эти механизмы позволяют: изменять скорости и законы движения звеньев и характер механического движения; осуществлять раздачу и суммирование движений; передавать движения между осями, произвольно расположенными в пространстве; осуществлять бесступенчатое изменение скорости движения.
К механизмам с высшими КП относятся зубчатые, кулачковые, фрикционные и волновые механизмы. К механизмам с низшими КП относятся рычажные, кулисные и синусные механизмы. Они более просты в изготовлении, но не обеспечивают высокой точности воспроизведения заданных законов движения. В дальнейшем будет рассмотрен синтез только плоских механизмов с высшими КП.
Слайд 4Тема 6
В этих механизмах элементы высших КП
являются либо центроидами, либо взаимоогибаемыми кривыми. В первом случае механизмы получили название центроидных. К механизмам, в которых элементы высших КП являются взаимоогибаемыми кривыми, относятся зубчатые и кулачковые механизмы.
6.2. Синтез зубчатых механизмов
6.2.1. Общая характеристика зубчатых механизмов
К зубчатым механизмам относятся механизмы, звенья в которых выполняются в виде зубчатых колес.
Зубчатыми колесами называются тела вращения (цилиндрические диски), на которых расположены зубья.
Зубчатые механизмы предназначены для передачи движения с одного вала на другой с постоянной либо переменной скоростями.
Их преимущества: компактность, минимальные
габаритные размеры; высокий КПД; практически любое
передаточное отношение (чаще всего постоянное);
высокая надежность, долговечность; простота эксплуатации.
6.2. Синтез зубчатых механизмов
6.2.1. Общая характеристика зубчатых механизмов
К зубчатым механизмам относятся механизмы, звенья в которых выполняются в виде зубчатых колес.
Зубчатыми колесами называются тела вращения (цилиндрические диски), на которых расположены зубья.
Зубчатые механизмы предназначены для передачи движения с одного вала на другой с постоянной либо переменной скоростями.
Их преимущества: компактность, минимальные
габаритные размеры; высокий КПД; практически любое
передаточное отношение (чаще всего постоянное);
высокая надежность, долговечность; простота эксплуатации.
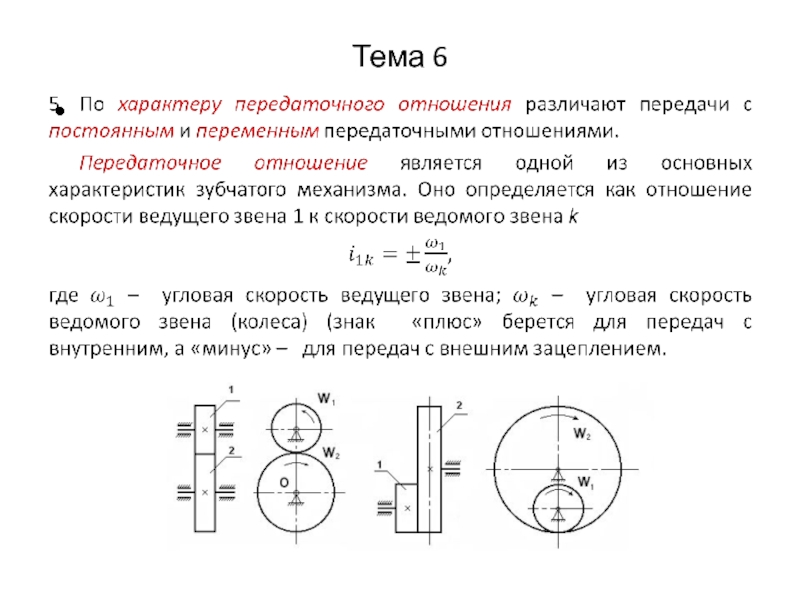
Слайд 5Тема 6
Различают простые и сложные зубчатые механизмы.
Простые зубчатые механизмы состоят из двух зубчатых колес. Часто их называют зубчатыми передачами или одноступенчатыми передачами (большее из колес называется зубчатым колесом, меньшее – шестерней).
Сложные зубчатые механизмы используются для получения больших передаточных отношений и образуются путем соединения нескольких одноступенчатых механизмов. Оси этих механизмов могут быть как неподвижными, так и подвижными. Механизмы с подвижными осями получили название планетарных.
Механизмы, понижающие угловую скорость, называются редукторами, повышающие – мультипликаторами.
Все сложные зубчатые механизмы можно классифицировать по характеру движения и подвижности осей валов, а также по величине передаточного отношения.
Сложные зубчатые механизмы используются для получения больших передаточных отношений и образуются путем соединения нескольких одноступенчатых механизмов. Оси этих механизмов могут быть как неподвижными, так и подвижными. Механизмы с подвижными осями получили название планетарных.
Механизмы, понижающие угловую скорость, называются редукторами, повышающие – мультипликаторами.
Все сложные зубчатые механизмы можно классифицировать по характеру движения и подвижности осей валов, а также по величине передаточного отношения.
Слайд 6Тема 6
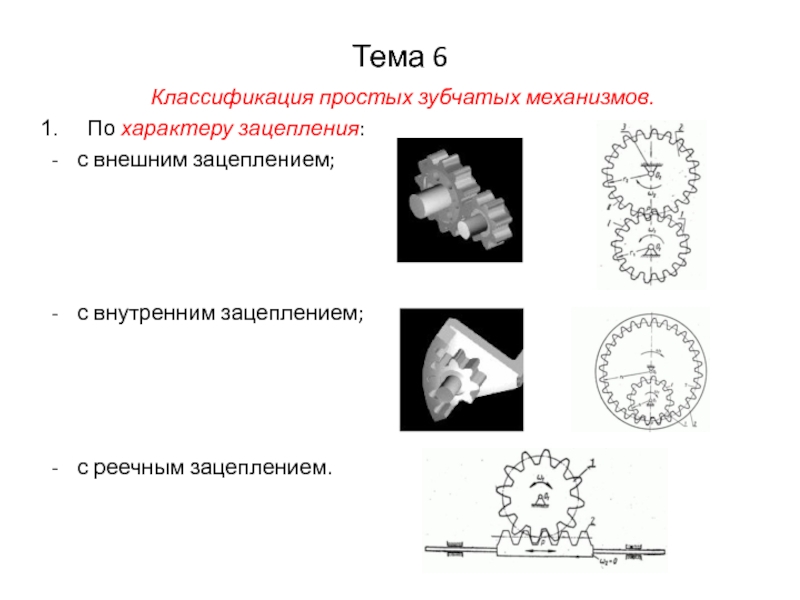
Классификация простых зубчатых механизмов.
По характеру зацепления:
с внешним зацеплением;
с внутренним зацеплением;
с
реечным зацеплением.
Слайд 7Тема 6
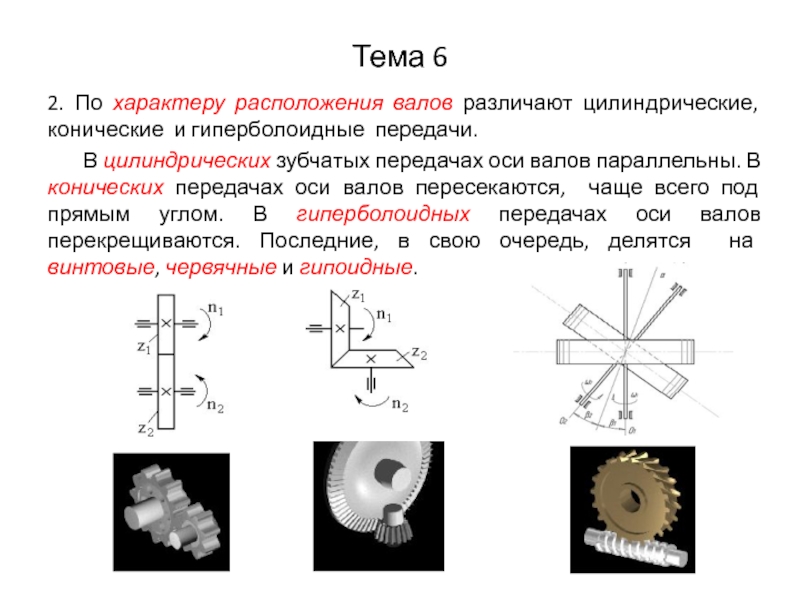
2. По характеру расположения валов различают цилиндрические, конические и гиперболоидные
передачи.
В цилиндрических зубчатых передачах оси валов параллельны. В конических передачах оси валов пересекаются, чаще всего под прямым углом. В гиперболоидных передачах оси валов перекрещиваются. Последние, в свою очередь, делятся на винтовые, червячные и гипоидные.
В цилиндрических зубчатых передачах оси валов параллельны. В конических передачах оси валов пересекаются, чаще всего под прямым углом. В гиперболоидных передачах оси валов перекрещиваются. Последние, в свою очередь, делятся на винтовые, червячные и гипоидные.
Слайд 8Тема 6
3. По типу взаимоогибаемых кривых, которыми очерчиваются боковые поверхности зубьев,
передачи делятся на эвольвентные, циклоидальные и передачи с круглым зубом.
Эвольвентный профиль – образуется как траектория точки касания прямой с окружностью при перекатывании этой прямой по окружности без скольжения. Передачи с циклоидальным зацеплением имеют профиль зуба, состоящий из участков циклоид, эпициклоид и гипоциклоид. Передачи с круглым зубом имеют профиль зуба в виде круга. Они обладают малой точностью, но позволяют передавать большие крутящие моменты.
4. По характеру расположения зубьев относительно образующей обода колеса передачи с эвольвентным зацеплением подразделяются на прямозубые, косозубые и шевронные.
Эвольвентный профиль – образуется как траектория точки касания прямой с окружностью при перекатывании этой прямой по окружности без скольжения. Передачи с циклоидальным зацеплением имеют профиль зуба, состоящий из участков циклоид, эпициклоид и гипоциклоид. Передачи с круглым зубом имеют профиль зуба в виде круга. Они обладают малой точностью, но позволяют передавать большие крутящие моменты.
4. По характеру расположения зубьев относительно образующей обода колеса передачи с эвольвентным зацеплением подразделяются на прямозубые, косозубые и шевронные.
Слайд 15Тема 6
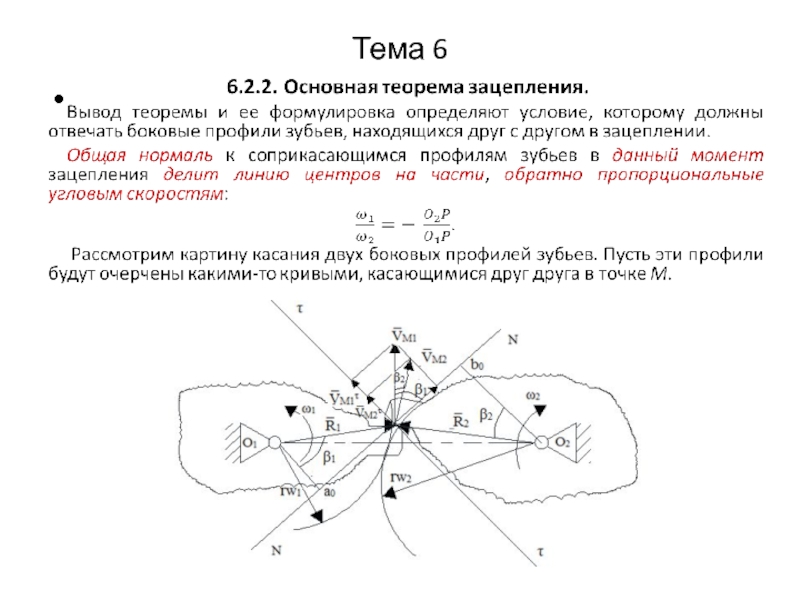
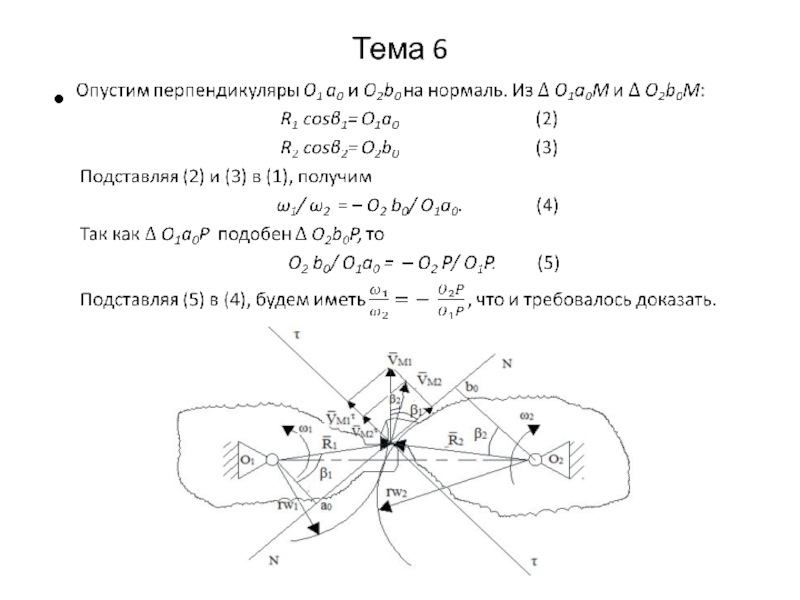
Основной теореме зацепления удовлетворяет большое число кривых.
Можно
вообще задаться профилем зуба одного колеса и, пользуясь теоремой, вычертить профиль зуба второго колеса. Однако полученное зацепление не всегда может удовлетворять всем требованиям, предъявляемым зацеплению: простота и технологичность производства; взаимозаменяемость колес; минимальный износ поверхностей зубьев и достаточная прочность; постоянство давления на опоры и т. д. Поэтому число профилей ограничено. Например, известен профиль проф. Новикова М.Л. (1958г.), за который тот получил Ленинскую премию.
Наибольшее распространение получил эвольвентный профиль, предложенный Л. Эйлером в 1754 году.
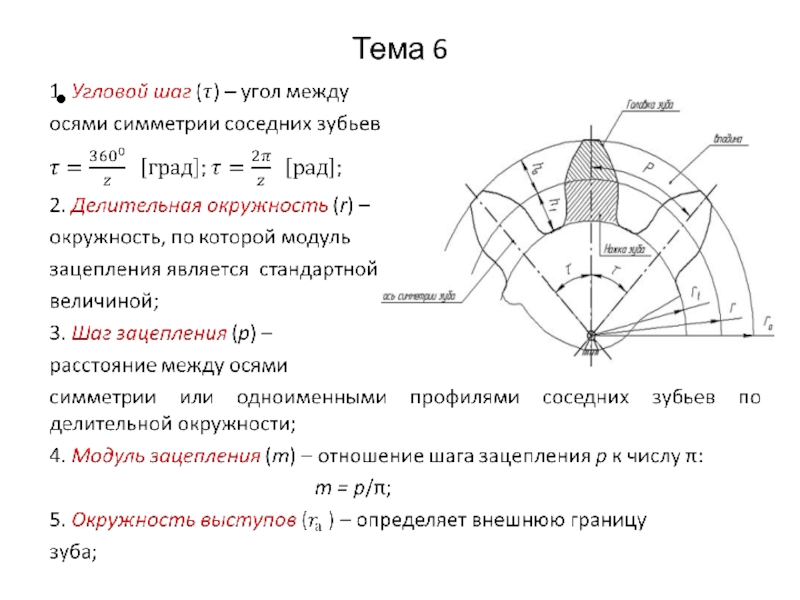
6.2.3. Основные геометрические параметры зубчатого колеса
Зубчатое колесо представляет собой цилиндрический диск с нарезанными на его поверхности зубьями, число которых равно z (см. рис.). Рассмотрим основные геометрические параметры этого колеса в плоскости, перпендикулярной оси вращения.
Каждый зуб колеса имеет ось симметрии, проходящую через ось его вращения О.
Наибольшее распространение получил эвольвентный профиль, предложенный Л. Эйлером в 1754 году.
6.2.3. Основные геометрические параметры зубчатого колеса
Зубчатое колесо представляет собой цилиндрический диск с нарезанными на его поверхности зубьями, число которых равно z (см. рис.). Рассмотрим основные геометрические параметры этого колеса в плоскости, перпендикулярной оси вращения.
Каждый зуб колеса имеет ось симметрии, проходящую через ось его вращения О.
Слайд 19Тема 6
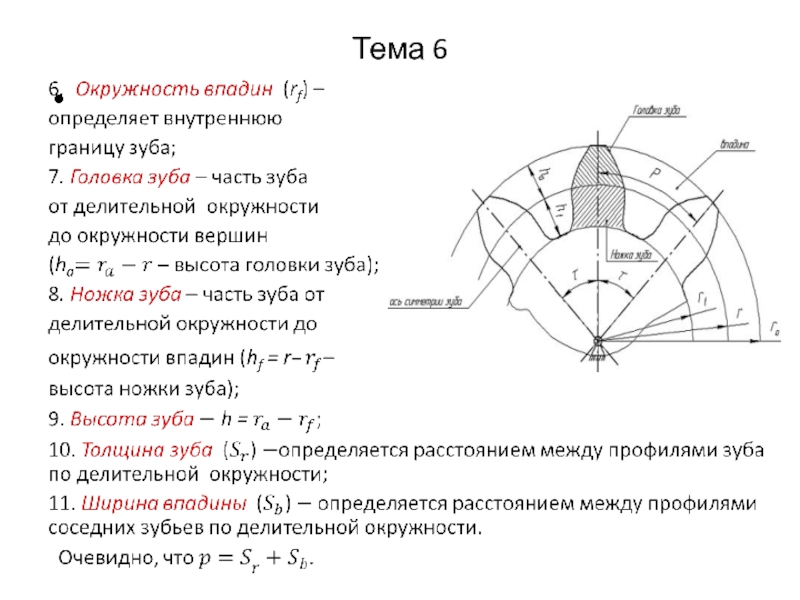
Остальные геометрические параметры этих зубчатых колес,
в соответствие с ГОСТом, выбираются пропорциональными модулю m:
высота головки зуба – ha = m;
высота ножки зуба – hf = 1,25 m;
высота зуба – h = ha+ hf = 2,25 m;
радиус окружности выступов
радиус окружности впадин
окружной шаг – p = π⋅m;
толщина зуба по делительной окружности
ширина впадины по делительной окружности
Ширину колеса принимают в пределах в = (10…30)m.
высота головки зуба – ha = m;
высота ножки зуба – hf = 1,25 m;
высота зуба – h = ha+ hf = 2,25 m;
радиус окружности выступов
радиус окружности впадин
окружной шаг – p = π⋅m;
толщина зуба по делительной окружности
ширина впадины по делительной окружности
Ширину колеса принимают в пределах в = (10…30)m.
Слайд 26Тема 6
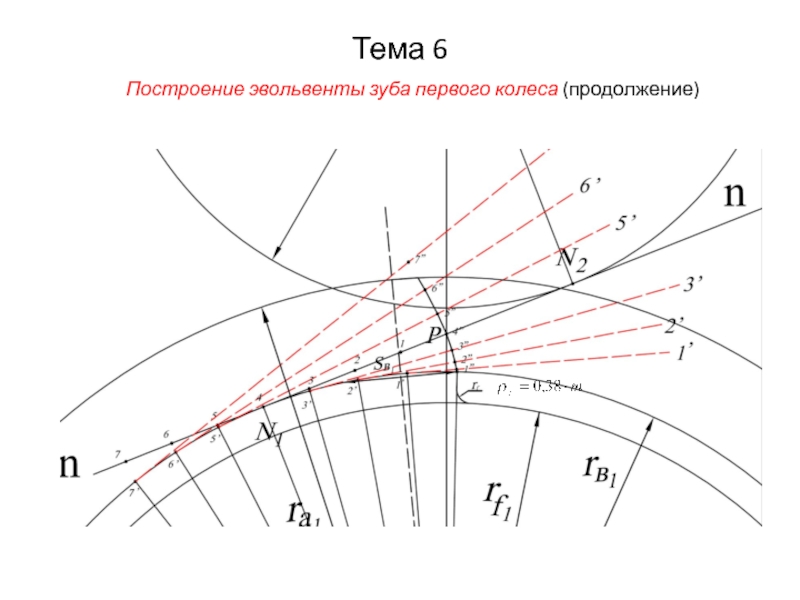
Построение эвольвенты зуба первого колеса
1) Отрезок PN1 линии зацепления делится
на несколько равных частей (отрезки P–1; 1–2; 2–3; 3–4 (N1 ). В противоположную сторону от т. N1 по линии зацепления также откладывается несколько отрезков (4–5; 5–6; 6–7);
2) Дугами, проведенными из т. N1 и равных длинам соответствующих отрезков, точки P, 1, 2, .. с линии зацепления переносятся на основную окружность первого колеса (Pl, 1l, 2l , …) и соединяются с т. О1 – осью вращения первого колеса;
3) Из тт. Pl, 1l, 2l , … проводятся касательные к основной окружности и на этих касательных откладываются отрезки:
; ; ; и т. д.;
4) Полученные точки соединяются плавной кривой, в результате чего образуется эвольвента бокового профиля зуба первого колеса (т. Pl – начало эвольвенты, точка возврата);
2) Дугами, проведенными из т. N1 и равных длинам соответствующих отрезков, точки P, 1, 2, .. с линии зацепления переносятся на основную окружность первого колеса (Pl, 1l, 2l , …) и соединяются с т. О1 – осью вращения первого колеса;
3) Из тт. Pl, 1l, 2l , … проводятся касательные к основной окружности и на этих касательных откладываются отрезки:
; ; ; и т. д.;
4) Полученные точки соединяются плавной кривой, в результате чего образуется эвольвента бокового профиля зуба первого колеса (т. Pl – начало эвольвенты, точка возврата);
Слайд 31Тема 6
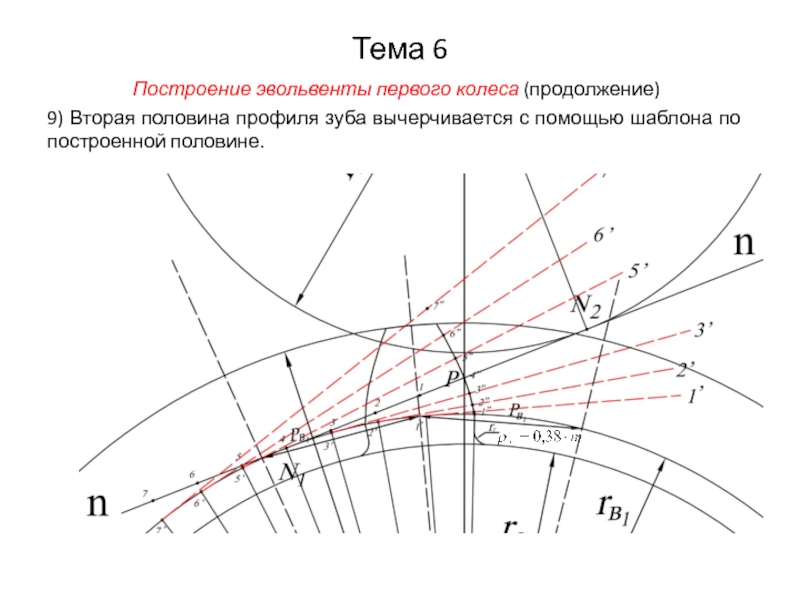
Построение эвольвенты первого колеса (продолжение)
9) Вторая половина профиля зуба вычерчивается
с помощью шаблона по построенной половине.
Слайд 32Тема 6
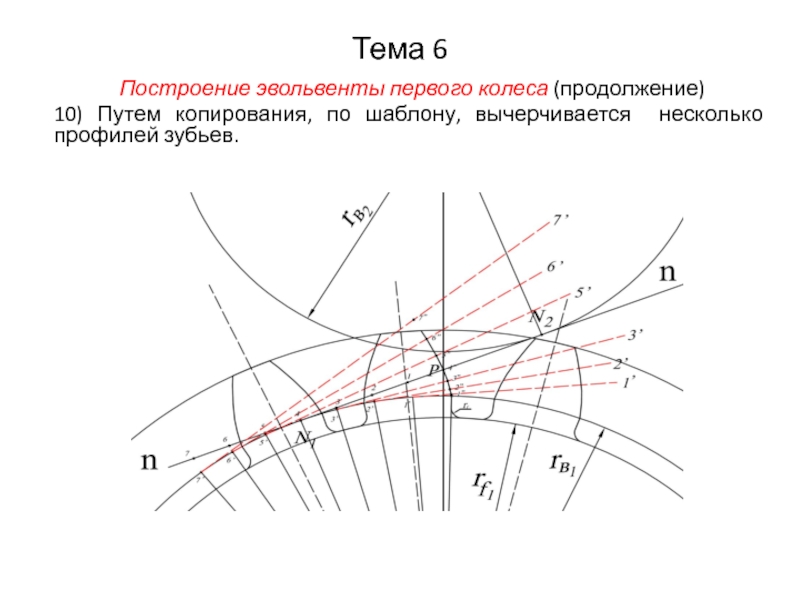
Построение эвольвенты первого колеса (продолжение)
10) Путем копирования, по шаблону, вычерчивается
несколько профилей зубьев.
Слайд 36Тема 6
Преимущества эвольвентного зацепления:
1. Линия зацепления – прямая, следовательно, эвольвентное зацепление
дает постоянное давление на опоры и подшипники валов;
2. Эвольвентное колесо может работать в паре с другим эвольвентным колесом, имеющим тот же модуль (коробка перемены передач);
3. Правильность эвольвентного зацепления сохраняется при небольших изменениях межосевого расстояния О1О2;
4. Эвольвентное зацепление обеспечивает возможность нарезания одним инструментом колес с разными числами зубьев.
5. Сумма радиусов кривизны сопряженных точек профилей зубьев есть величина постоянная и равная длине теоретического участка линии зацепления (N1N2).
Недостатки эвольвентного зацепления:
1. Эвольвентное зацепление приводит к большому износу зубьев;
2. Малая поверхностная прочность эвольвентных профилей.
2. Эвольвентное колесо может работать в паре с другим эвольвентным колесом, имеющим тот же модуль (коробка перемены передач);
3. Правильность эвольвентного зацепления сохраняется при небольших изменениях межосевого расстояния О1О2;
4. Эвольвентное зацепление обеспечивает возможность нарезания одним инструментом колес с разными числами зубьев.
5. Сумма радиусов кривизны сопряженных точек профилей зубьев есть величина постоянная и равная длине теоретического участка линии зацепления (N1N2).
Недостатки эвольвентного зацепления:
1. Эвольвентное зацепление приводит к большому износу зубьев;
2. Малая поверхностная прочность эвольвентных профилей.
Слайд 37Тема 6
6.2.6. Методы изготовления зубчатых колес
Существует два
принципиально различных метода: метод копирования и метод обкатки (огибания).
К методу копирования относятся:
литье, штамповка, протягивание, строгание,
фрезерование пальцевой и дисковой фрезами
и шлифование. При этом методе форма
режущих кромок инструмента отвечает
форме впадины между зубьями колеса.
За один проход инструмента нарезается одна впадина. Для вырезания следующей впадины заготовку 2 поворачивают на величину углового шага. Недостатками метода копирования являются невысокие точность, производительность и универсальность, т. е. невозможность нарезания одним инструментом зубчатых колес с различными числами зубьев, что требует большого количества зуборезного инструмента.
Основное применение этот метод получил в мелкосерийном, единичном и ремонтном производствах, а также для изготовления крупных зубчатых колес.
К методу копирования относятся:
литье, штамповка, протягивание, строгание,
фрезерование пальцевой и дисковой фрезами
и шлифование. При этом методе форма
режущих кромок инструмента отвечает
форме впадины между зубьями колеса.
За один проход инструмента нарезается одна впадина. Для вырезания следующей впадины заготовку 2 поворачивают на величину углового шага. Недостатками метода копирования являются невысокие точность, производительность и универсальность, т. е. невозможность нарезания одним инструментом зубчатых колес с различными числами зубьев, что требует большого количества зуборезного инструмента.
Основное применение этот метод получил в мелкосерийном, единичном и ремонтном производствах, а также для изготовления крупных зубчатых колес.
Слайд 38Тема 6
Наибольшее применение получил метод обкатки. К
этому методу относятся: фрезерование червячной фрезой, обработка долбяком, обработка рейкой, накатка зубьев, шлифование, шевингование.
При этом методе форма режущего инструмента схожа с формой зубчатого колеса или рейки, зубьям которых приданы режущие свойства, а относительные движение заготовки колеса и режущего инструмента такие же, как при зацеплении нарезаемого колеса с другим зубчатым колесом или рейкой. Такие инструменты получили название инструментального колеса (долбяка, шевера) или инструментальной рейки.
Процесс нарезания колес осуществляется
на специальных зуборезных станках,
которые обеспечивают принудительное
взаимное перемещение инструмента и
заготовки колеса. Преимущество
метода обкатки заключается в
возможности нарезания одним
инструментом зубчатых колес с различными числами зубьев.
При этом методе форма режущего инструмента схожа с формой зубчатого колеса или рейки, зубьям которых приданы режущие свойства, а относительные движение заготовки колеса и режущего инструмента такие же, как при зацеплении нарезаемого колеса с другим зубчатым колесом или рейкой. Такие инструменты получили название инструментального колеса (долбяка, шевера) или инструментальной рейки.
Процесс нарезания колес осуществляется
на специальных зуборезных станках,
которые обеспечивают принудительное
взаимное перемещение инструмента и
заготовки колеса. Преимущество
метода обкатки заключается в
возможности нарезания одним
инструментом зубчатых колес с различными числами зубьев.
Слайд 39Тема 6
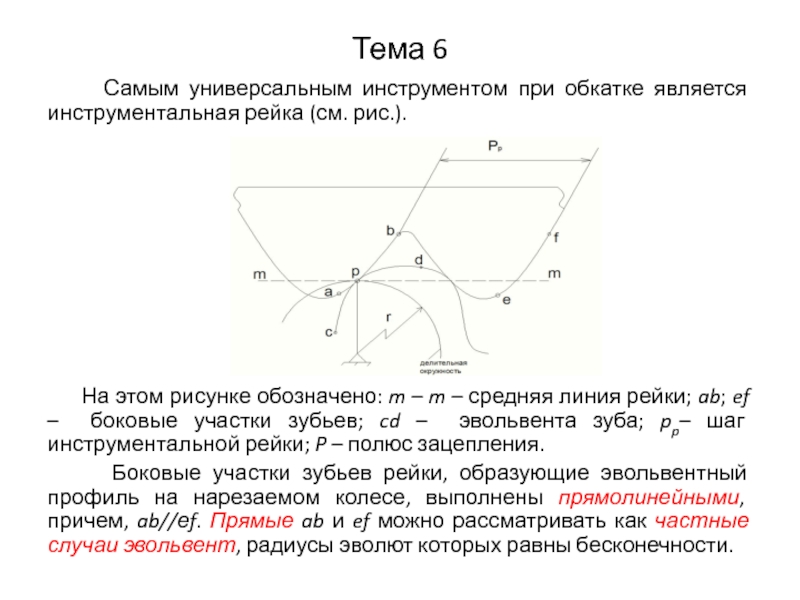
Самым универсальным инструментом при обкатке является инструментальная
рейка (см. рис.).
На этом рисунке обозначено: m – m – средняя линия рейки; ab; ef – боковые участки зубьев; cd – эвольвента зуба; pp– шаг инструментальной рейки; P – полюс зацепления.
Боковые участки зубьев рейки, образующие эвольвентный профиль на нарезаемом колесе, выполнены прямолинейными, причем, ab//еf. Прямые ab и ef можно рассматривать как частные случаи эвольвент, радиусы эволют которых равны бесконечности.
На этом рисунке обозначено: m – m – средняя линия рейки; ab; ef – боковые участки зубьев; cd – эвольвента зуба; pp– шаг инструментальной рейки; P – полюс зацепления.
Боковые участки зубьев рейки, образующие эвольвентный профиль на нарезаемом колесе, выполнены прямолинейными, причем, ab//еf. Прямые ab и ef можно рассматривать как частные случаи эвольвент, радиусы эволют которых равны бесконечности.
Слайд 41Тема 6
Значения модуля зацепления выбираются из стандартных рядов (в
мм):
1-й ряд – 1;1.25;1.5;2;2.5;3;4;5;6;8;10;12;16;20;25;32;40;50;60;80;100;
2-ой ряд – 1.125;1.375;1.75;2.25;2.75;3.5;4.5;5.5;7;9;11;14;18;22;28;36.
Размеры инструментальной рейки также стандартизованы в долях модуля. ГОСТ 13755–81 предусматривает два варианта исполнения рейки: основной и укороченный контуры.
Обозначения на рис.: α – угол профиля рейки; mm – средняя линия рейки; ab; ef – боковые участки зубьев; Pp– шаг инструментальной рейки; c* – коэффициент радиального зазора; ha* – коэффициент высоты зуба; Sp–толщина зуба рейки.
1-й ряд – 1;1.25;1.5;2;2.5;3;4;5;6;8;10;12;16;20;25;32;40;50;60;80;100;
2-ой ряд – 1.125;1.375;1.75;2.25;2.75;3.5;4.5;5.5;7;9;11;14;18;22;28;36.
Размеры инструментальной рейки также стандартизованы в долях модуля. ГОСТ 13755–81 предусматривает два варианта исполнения рейки: основной и укороченный контуры.
Обозначения на рис.: α – угол профиля рейки; mm – средняя линия рейки; ab; ef – боковые участки зубьев; Pp– шаг инструментальной рейки; c* – коэффициент радиального зазора; ha* – коэффициент высоты зуба; Sp–толщина зуба рейки.
Слайд 43Тема 6
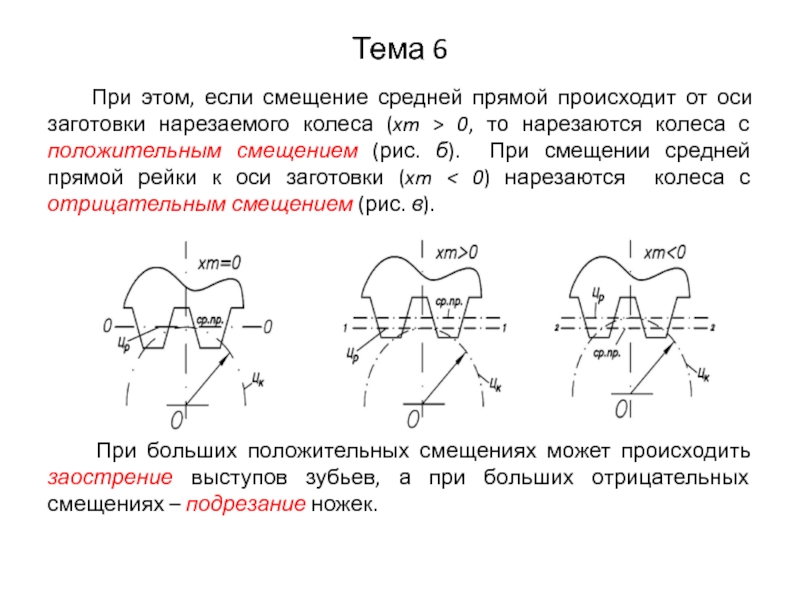
При этом, если смещение средней прямой происходит
от оси заготовки нарезаемого колеса (xm > 0, то нарезаются колеса с положительным смещением (рис. б). При смещении средней прямой рейки к оси заготовки (xm < 0) нарезаются колеса с отрицательным смещением (рис. в).
При больших положительных смещениях может происходить заострение выступов зубьев, а при больших отрицательных смещениях – подрезание ножек.
При больших положительных смещениях может происходить заострение выступов зубьев, а при больших отрицательных смещениях – подрезание ножек.
Слайд 46Тема 6
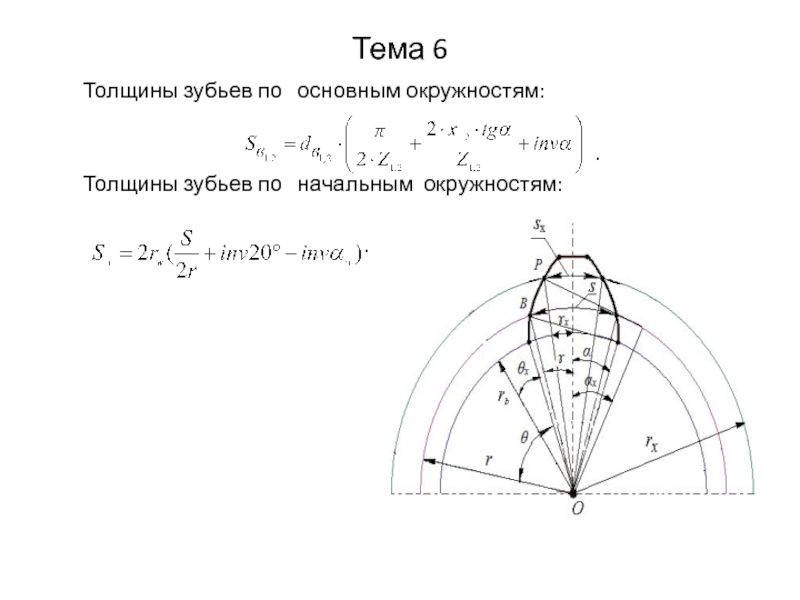
Толщины зубьев по основным окружностям:
.
Толщины зубьев по начальным окружностям:
. ..
Толщины зубьев по начальным окружностям:
. ..
Слайд 47Тема 6
6.2.8. Определение угла зацепления
Пользуясь полученной формулой,
можно выразить толщину зуба по начальной окружности:
Так как , , , то
По условиям обкатки, т. е. при беззазорном зацеплении, сумма толщин зубьев по начальным окружностям отвечает условию , или
откуда получим зависимость для определения угла зацепления
Так как , , , то
По условиям обкатки, т. е. при беззазорном зацеплении, сумма толщин зубьев по начальным окружностям отвечает условию , или
откуда получим зависимость для определения угла зацепления
Слайд 48Тема 6
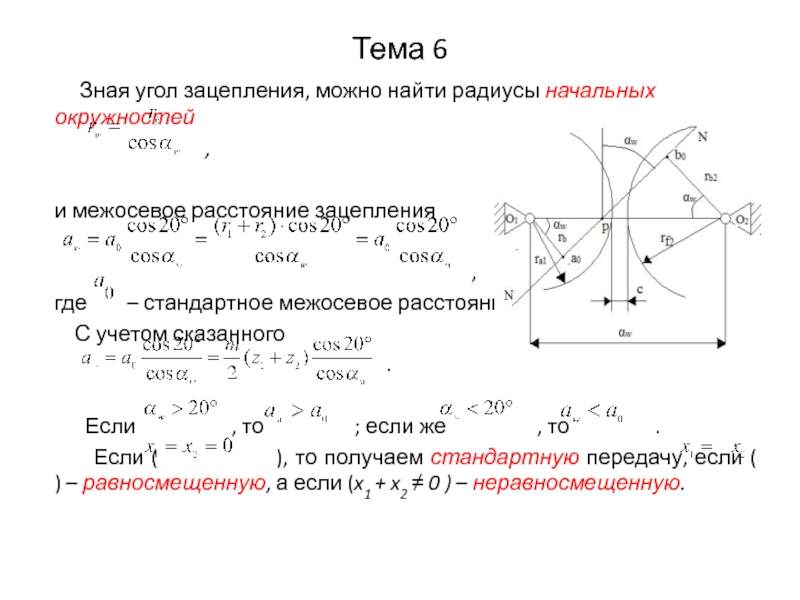
Зная угол зацепления, можно найти радиусы начальных
окружностей
,
и межосевое расстояние зацепления
,
где – стандартное межосевое расстояние.
С учетом сказанного
.
Если , то ; если же , то .
Если ( ), то получаем стандартную передачу, если ( ) – равносмещенную, а если (x1 + x2 ≠ 0 ) – неравносмещенную.
,
и межосевое расстояние зацепления
,
где – стандартное межосевое расстояние.
С учетом сказанного
.
Если , то ; если же , то .
Если ( ), то получаем стандартную передачу, если ( ) – равносмещенную, а если (x1 + x2 ≠ 0 ) – неравносмещенную.
Слайд 49Тема 6
6.2.9. Определение радиусов окружностей впадин и выступов
Радиусы
окружностей впадин вычисляются по формуле
,
Знак «+» принимается при положительном смещении, а «-» – при отрицательном.
Радиусы окружности выступов определяются из условия сохранения радиального зазора с, при плотном зацеплении зубьев. Величина радиального зазора по ГОСТ 13755-81 составляет c = 0,25m. Поэтому эти радиусы вычисляются по формуле
.
,
Знак «+» принимается при положительном смещении, а «-» – при отрицательном.
Радиусы окружности выступов определяются из условия сохранения радиального зазора с, при плотном зацеплении зубьев. Величина радиального зазора по ГОСТ 13755-81 составляет c = 0,25m. Поэтому эти радиусы вычисляются по формуле
.
Слайд 50Тема 6
6.2.10. Виды зацепления колес
В зависимости от
того, какие зубчатые колеса введены в зацепление, образуется три вида зацепления:
1. Нулевое зацепление (x1=x2=0). В этом случае делительные окружности совпадают с начальными, угол зацепления равен углу профиля рейки и толщина зуба по начальной окружности равна ширине впадины;
2. Смещенно – нулевое зацепление (x1+x2=0; x1 = -x2).В таком зацеплении делительные окружности также совпадают с начальными, угол зацепления равен углу профиля рейки, но толщины зубьев по начальным (делительным) окружностям не равны между собой;
3. Смещенное зацепление (x1 + x2 ≠ 0). В этом зацепленииделительные окружности не совпадают с начальными, угол зацепления отличается от угла профиля рейки и толщины зубьев по делительным окружностям неодинаковы.
1. Нулевое зацепление (x1=x2=0). В этом случае делительные окружности совпадают с начальными, угол зацепления равен углу профиля рейки и толщина зуба по начальной окружности равна ширине впадины;
2. Смещенно – нулевое зацепление (x1+x2=0; x1 = -x2).В таком зацеплении делительные окружности также совпадают с начальными, угол зацепления равен углу профиля рейки, но толщины зубьев по начальным (делительным) окружностям не равны между собой;
3. Смещенное зацепление (x1 + x2 ≠ 0). В этом зацепленииделительные окружности не совпадают с начальными, угол зацепления отличается от угла профиля рейки и толщины зубьев по делительным окружностям неодинаковы.