- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
§8. Плоскопараллельное движение твердого тела (плоское) презентация
Содержание
- 1. §8. Плоскопараллельное движение твердого тела (плоское)
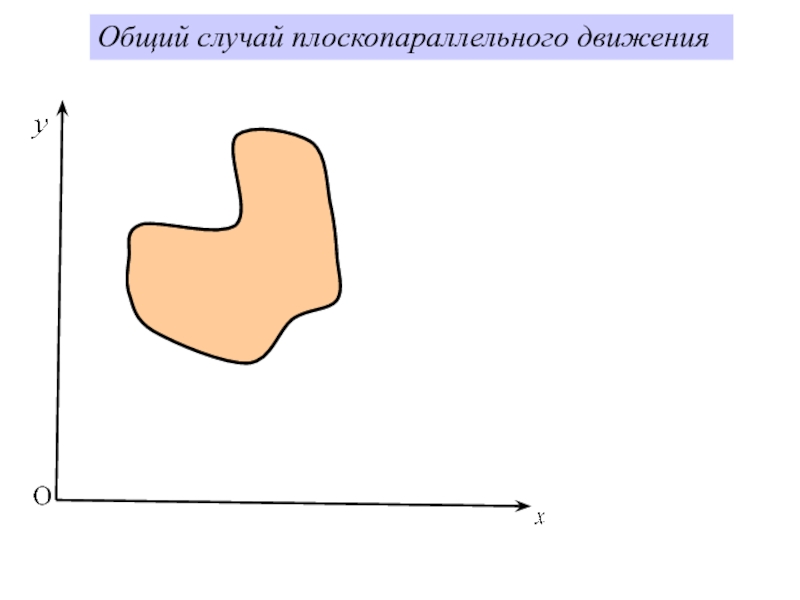
- 2. Общий случай плоскопараллельного движения О
- 4. Скорость произвольной точки плоской фигуры равна геометрической
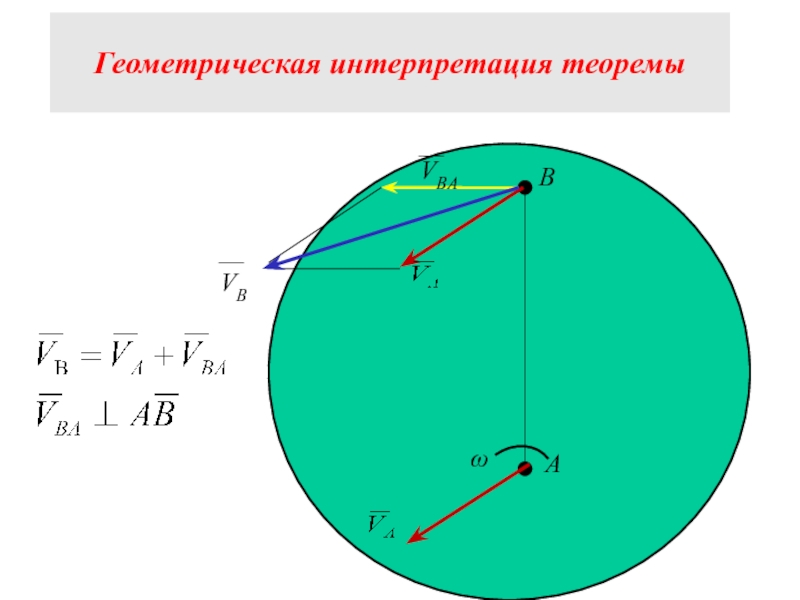
- 5. Геометрическая интерпретация теоремы А В ω VBA VB
- 6. 8.5. Мгновенный центр скоростей Мгновенным центром скоростей
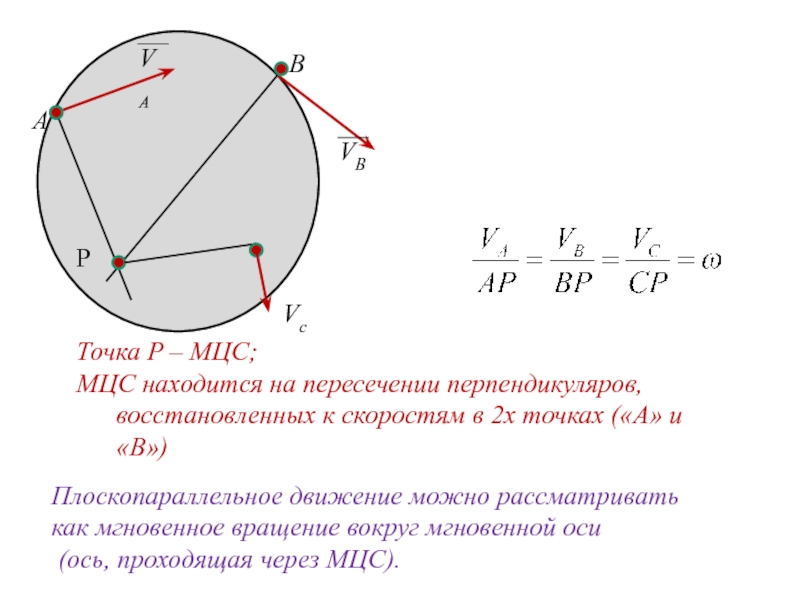
- 7. P A B VB VA Точка
- 8. Скорости двух точек тела параллельны друг другу,
- 9. Скорости двух точек параллельны, но не перпендикулярны
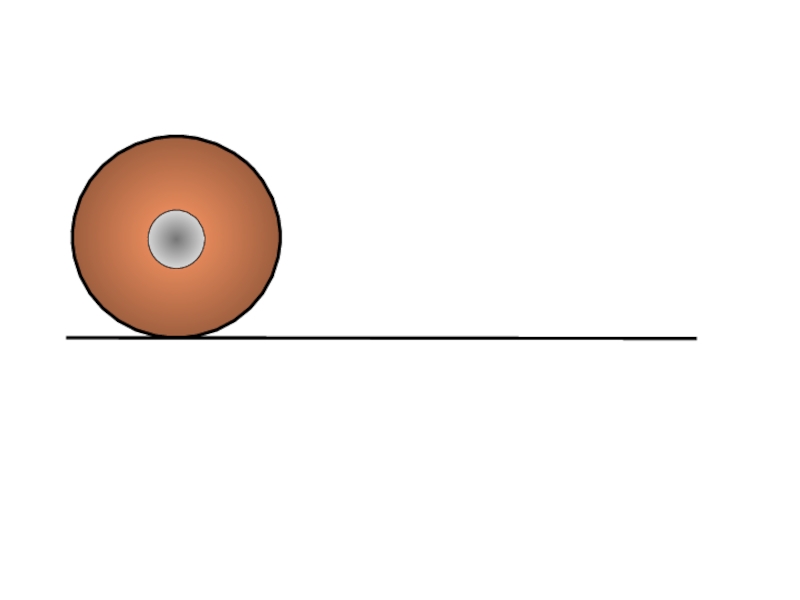
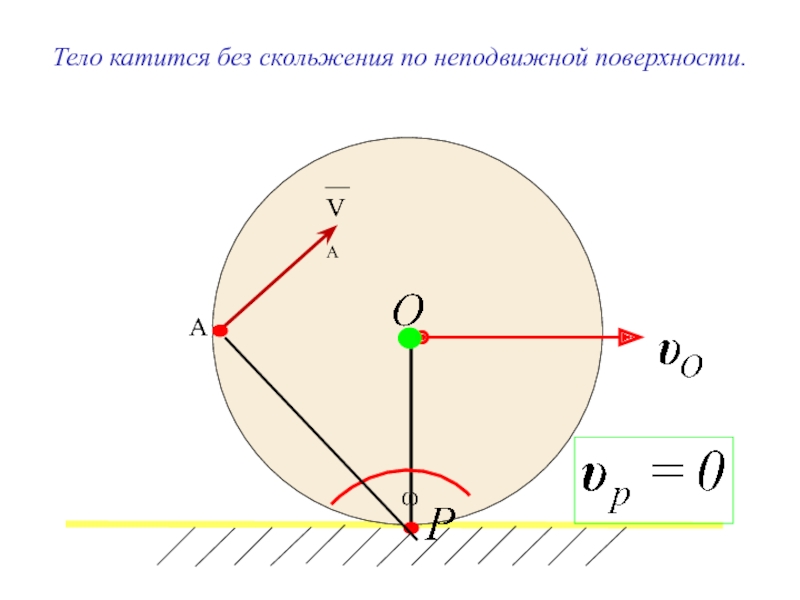
- 10. Тело катится без скольжения по неподвижной поверхности.
- 12. Теорема о сложении ускорений точек при плоскопараллельном
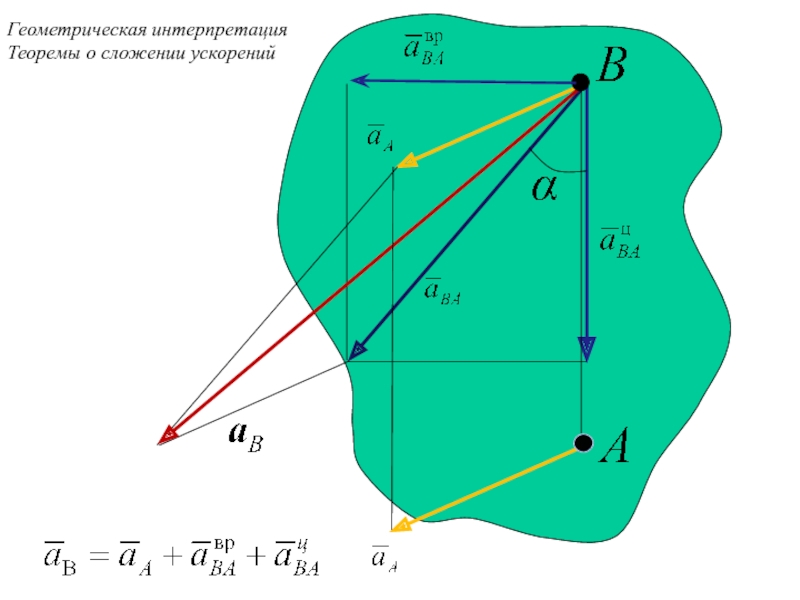
- 13. Геометрическая интерпретация Теоремы о сложении ускорений
- 14. Аналитическое определение ускорений 1. Направление движения (.)
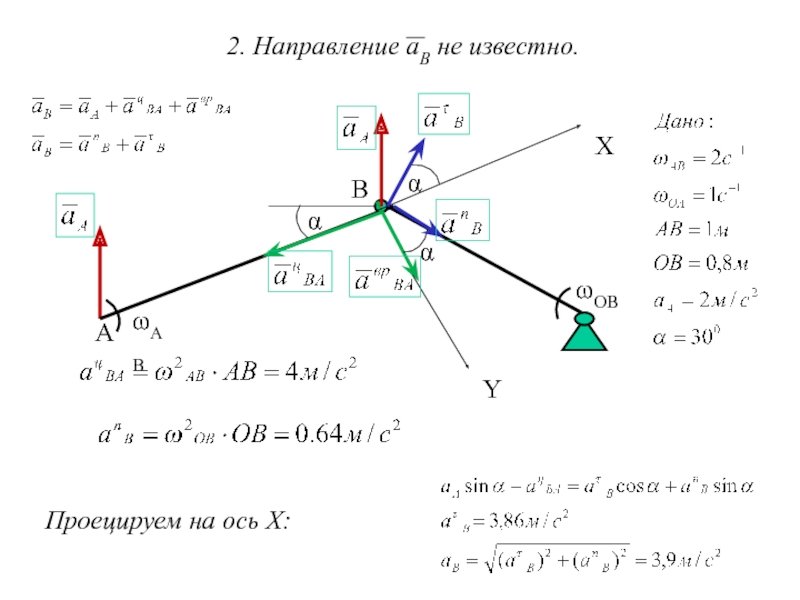
- 15. 2. Направление аВ не известно.
- 16. 3. Движение диска без скольжения. Дано:
- 17. Кинематический анализ плоского механизма. Найти для заданного
- 18. Кинематический анализ плоского механизма. Построение плана скоростей
- 19. Свойства плана скоростей Одноименные отрезки плана скоростей
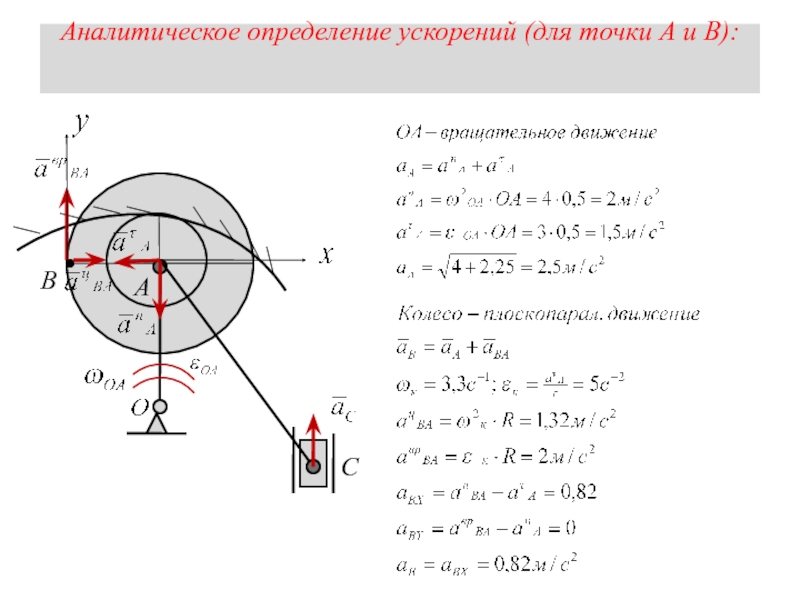
- 20. Аналитическое определение ускорений (для точки А и
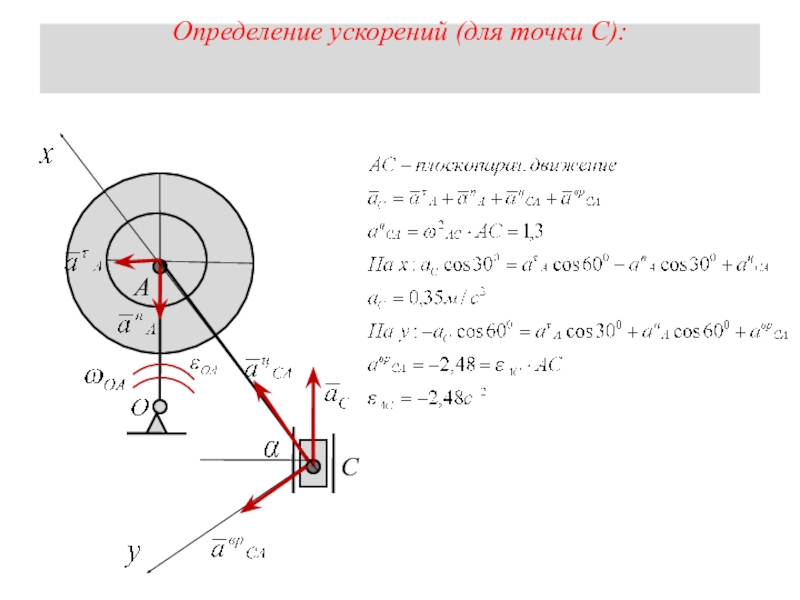
- 21. Определение ускорений (для точки С):
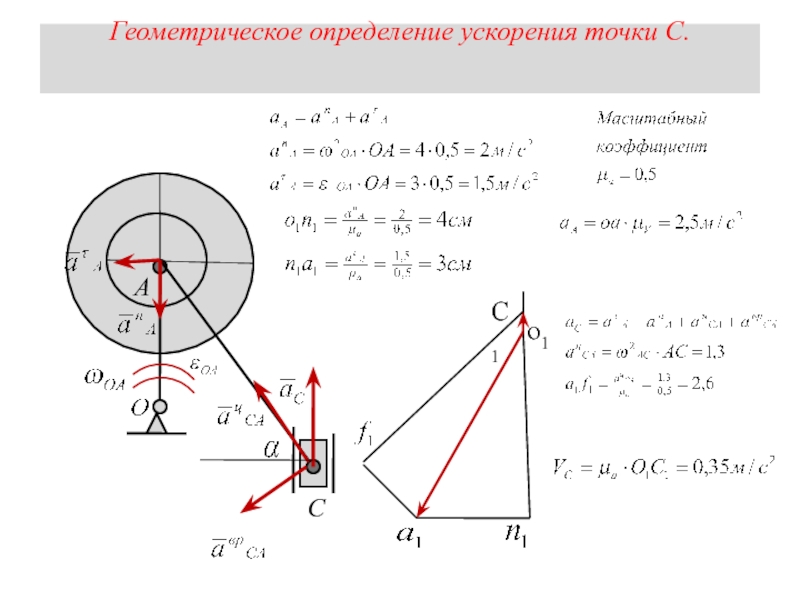
- 22. Геометрическое определение ускорения точки С.
Слайд 1§8. Плоскопараллельное движение твердого тела (плоское)
Плоскопараллельным (плоским) движением твердого тела называется
Слайд 4Скорость произвольной точки плоской фигуры равна геометрической сумме скорости полюса и
Теорема о скоростях точек тела при
плоскопараллельном движении
Слайд 68.5. Мгновенный центр скоростей
Мгновенным центром скоростей (МЦС) называется точка связанная с
Слайд 7
P
A
B
VB
VA
Точка P – МЦС;
МЦС находится на пересечении перпендикуляров, восстановленных к скоростям
Vс
Плоскопараллельное движение можно рассматривать
как мгновенное вращение вокруг мгновенной оси
(ось, проходящая через МЦС).
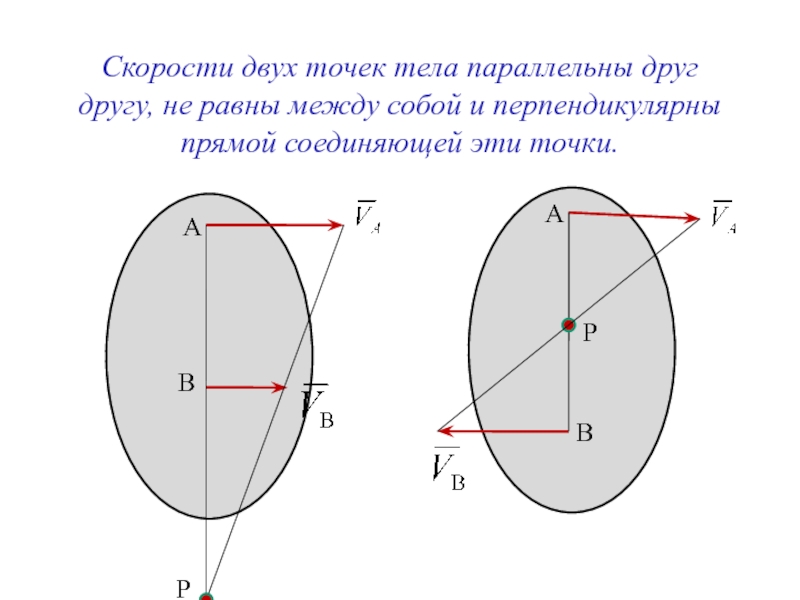
Слайд 8Скорости двух точек тела параллельны друг другу, не равны между собой
А
В
А
В
Р
Р
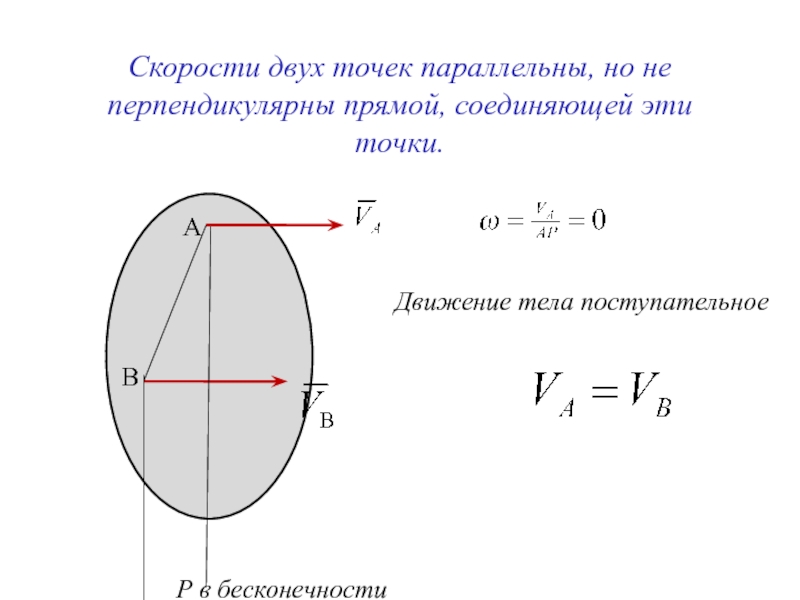
Слайд 9Скорости двух точек параллельны, но не перпендикулярны прямой, соединяющей эти точки.
А
В
Р
Движение тела поступательное
Слайд 11
O
O
O
A
A
A
B
B
B
VA
VA
VA
C
C
C
VB
VB
VB
VC
VC
VC
ωOA
ωOA
ωOA
ωAB = 0
ωAB
ωAB
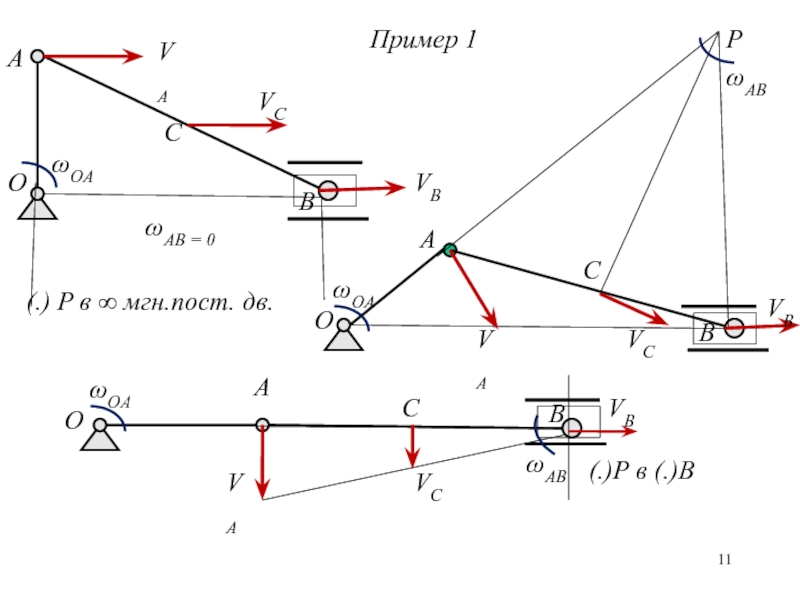
(.) P в ∞ мгн.пост. дв.
(.)P в
P
Пример 1
Слайд 12Теорема о сложении ускорений точек при плоскопараллельном движении тела
Ускорение произвольной точки
при его плоскопараллельном движении равно
векторной сумме ускорения полюса, вращательного
и центростремительного ускорений этой точки
при вращении вокруг полюса.
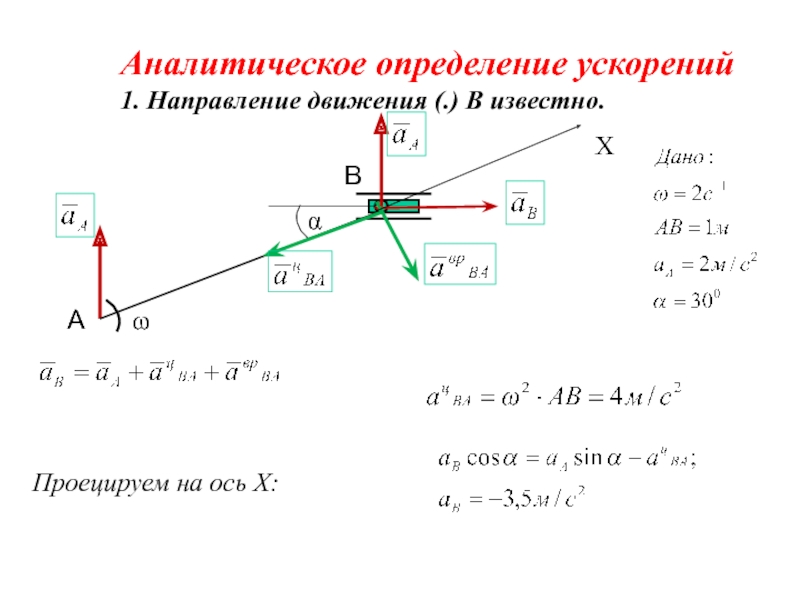
Слайд 14Аналитическое определение ускорений
1. Направление движения (.) В известно.
α
ω
X
Проецируем на ось X:
А
В
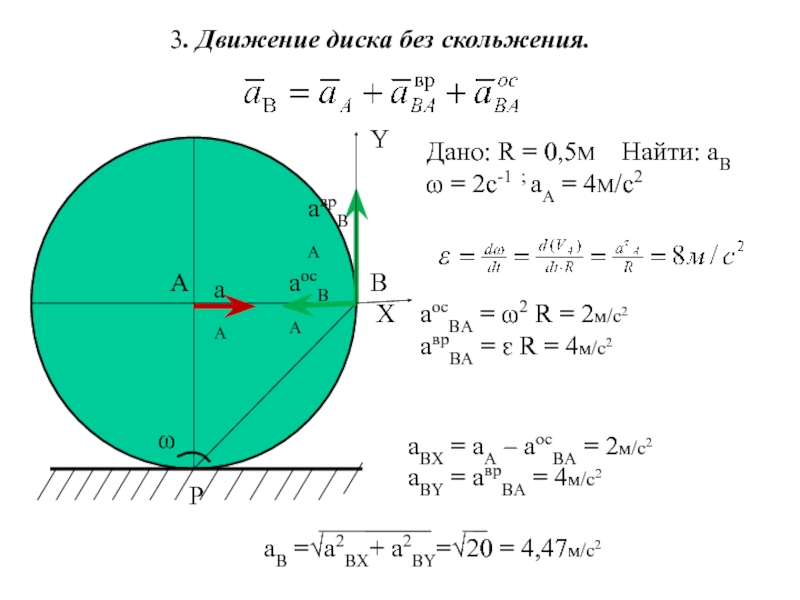
Слайд 163. Движение диска без скольжения.
Дано: R = 0,5M Найти: aB
ω
A
aA
P
ω
aocBA = ω2 R = 2м/с2
aврBA = ԑ R = 4м/с2
B
X
Y
aocBA
aврBA
aBX = aA – aocBA = 2м/с2
aBY = aврBA = 4м/с2
aB =√a2BX+ a2BY=√20 = 4,47м/c2
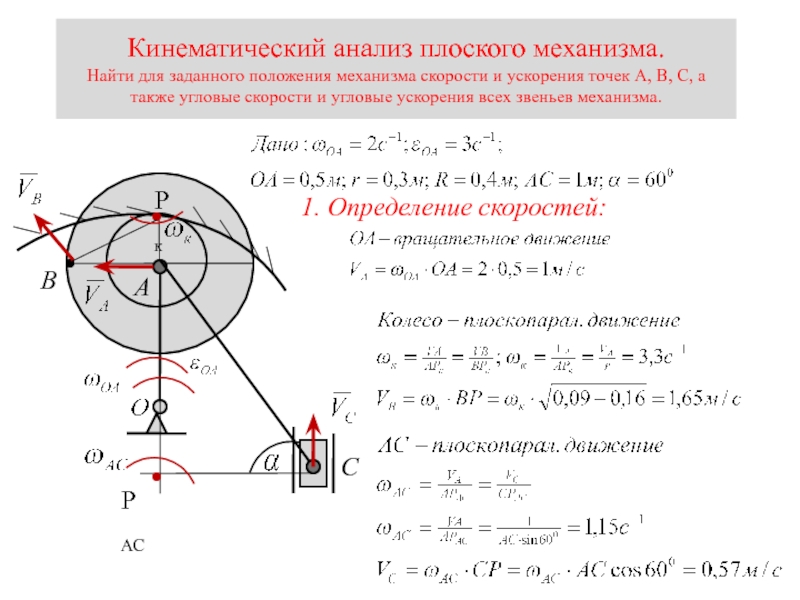
Слайд 17Кинематический анализ плоского механизма. Найти для заданного положения механизма скорости и ускорения
Рк
РАС
А
В
С
1. Определение скоростей:
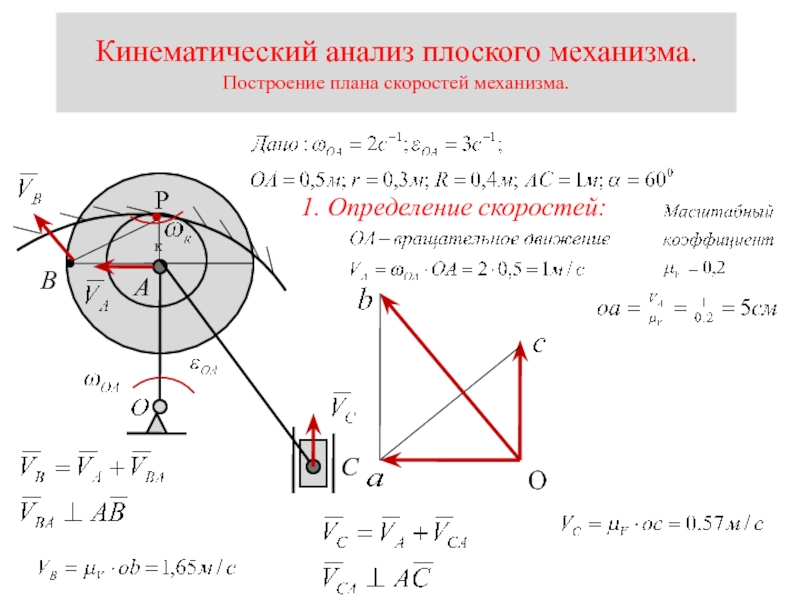
Слайд 18Кинематический анализ плоского механизма.
Построение плана скоростей механизма.
Рк
А
В
С
1. Определение скоростей:
O
Слайд 19Свойства плана скоростей
Одноименные отрезки плана скоростей и механизма
взаимно перпендикулярны.
2. Одноименные
прямо пропорциональны.
3. Одноименные фигуры плана скоростей и механизма подобны
и повернуты друг относительно друга на угол 900