- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стоимостная оценка риска на основе концепции Value-at-Risk (VaR) презентация
Содержание
- 1. Стоимостная оценка риска на основе концепции Value-at-Risk (VaR)
- 2. Опыт показывает, что вероятность возникновения ситуации, приводящей
- 3. Для получения нестрессовой оценки рыночного риска, имеющей
- 4. Value-at-Risk (VaR) – денежная оценка максимальных ожидаемых
- 5. VaR – это выраженная в данных денежных
- 6. Временной горизонт удержания позиции – минимальная сумма
- 7. Глубина периодов расчета VaR – это объем
- 8. Доверительный интервал и временной горизонт являются ключевыми
- 9. 1) «локальное оценивание» – линейная или более
- 10. - для расчета лимитов по открытым позициям;
- 11. это процедура, позволяющая установить степень адекватности модели
- 12. 2. Основные методы расчета VaR, их достоинства
- 13. Получить оценку VaR в замкнутом виде. В
- 14. В случае нормально распределенной случайной величины доверительный
- 15. Статистическая оценка максимальных отрицательных отклонений рыночной стоимости
- 16. - квантиль отсечения для α (ДАЛЕЕ
- 18. Квантили нормального распределения
- 19. Параметрический метод :
- 20. - сравнительная простота реализации; - сравнительно небольшие
- 21. - низкая точность оценки риска нелинейных инструментов,
- 22. Относится к группе методов полного оценивания и
- 23. Для каждого из этих Т сценариев изменений
- 24. После этого полученные Т изменений портфеля ранжируются
- 25. - Отсутствие предположений о нормальном распределении доходностей
- 26. - Использование только одной траектории эволюции цен;
- 29. Моделирование случайных процессов (траектории цен) с заданными
- 30. Траектория цен – это последовательность псевдослучайным образом
- 31. Существует вариант метода Монте-Карло, при котором для
- 32. - Высокая точность расчетов; - Высокая точность
- 33. - Высокая сложность моделей и соответственно высокий
Слайд 1Тема 4: Стоимостная оценка риска на основе концепции Value-at-Risk (VaR)
1. Понятие
2. Методы расчета VaR, их достоинства и недостатки.
Слайд 2Опыт показывает, что вероятность возникновения ситуации, приводящей к большим потерям на
Слайд 3Для получения нестрессовой оценки рыночного риска, имеющей практическую ценность, из рассмотрения
Слайд 4Value-at-Risk (VaR) – денежная оценка максимальных ожидаемых потерь по открытым позициям,
Слайд 5VaR – это выраженная в данных денежных единицах (базовой валюте) оценка
Показатель VaR обычно не используется применительно к рынкам, находящимся в состоянии кризиса.
VaR – это наибольший ожидаемый убыток, обусловленный колебаниями цен на финансовых рынках, который рассчитывается:
- на определенный период времени в будущем (временной горизонт);
- с заданной вероятностью его не превышения (уровень доверия);
- при данном предположении о характере поведения рынка (метод расчета).
Слайд 6Временной горизонт удержания позиции – минимальная сумма времени на принятие решения
Слайд 7Глубина периодов расчета VaR – это объем ретроспективных или симулированных данных,
Уровень доверия (доверительный интервал)) – вероятность наступления (или ненаступления) какого-либо события.
Слайд 8Доверительный интервал и временной горизонт являются ключевыми параметрами, без которых невозможны
Так, значение VaR в 10 млн р. для временного горизонта в один день и доверительного интервала 99 % будет означать (при условии сохранения тенденций рыночной конъюнктуры):
- вероятность того, что в течение следующих 24 часов мы потеряем не более чем 10 млн р., составляет 99 %;
- вероятность того, что наши убытки превысят 10 млн р. в течение ближайших суток, равна 1 %;
- убытки, превышающие 10 млн р., ожидаются в среднем один раз в 100 дней торгов.
Слайд 91) «локальное оценивание» – линейная или более сложная аппроксимация функции стоимости
2) «полное оценивание» - полный пересчет стоимости финансового инструмента без аппроксимирующих предположений. К этой группе относятся метод исторического моделирования и метод Монте-Карло.
Существуют 2 основные группы подходов к оценке VaR:
Слайд 10 - для расчета лимитов по открытым позициям;
- для расчета достаточности капитала
- для оценки доходности операций с учетом риска.
Показатель VaR используется в риск- менеджменте в следующих целях:
Слайд 11 это процедура, позволяющая установить степень адекватности модели оценки рыночного риска в
Верификация моделей расчета VaR по историческим данным -
Слайд 122. Основные методы расчета VaR, их достоинства и недостатки.
Исторически понятие Value
Слайд 13 Получить оценку VaR в замкнутом виде. В его основе лежит посылка
Дельта-нормальный метод расчета величины VaR позволяет
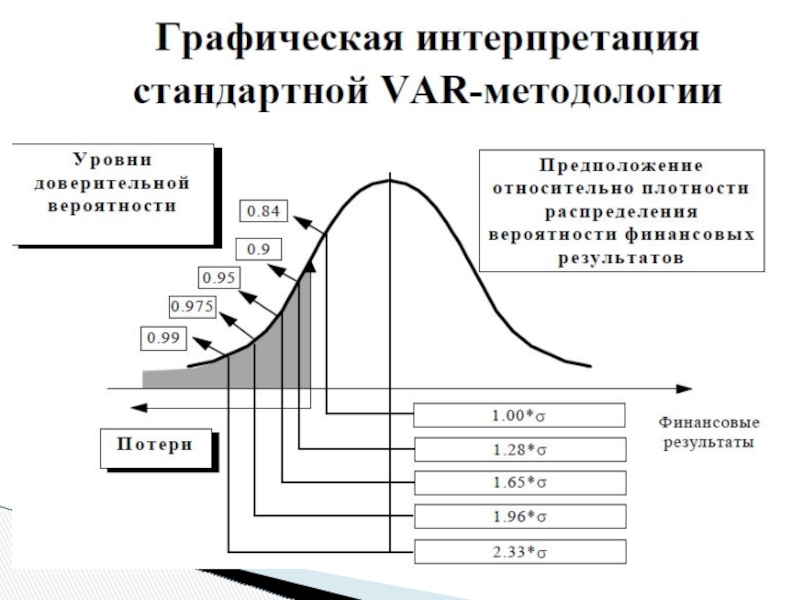
Слайд 14 В случае нормально распределенной случайной величины доверительный интервал (1-α) всегда характеризуется
Слайд 15Статистическая оценка максимальных отрицательных отклонений рыночной стоимости портфеля из одного актива
где
- рыночная стоимость на дату t портфеля данного актива;
- статистическая оценка математического ожидания функции доходности Rt
Слайд 16 - квантиль отсечения для α (ДАЛЕЕ ГРАФИК И ТАБЛИЦА);
- статистическая
- доходность актива за период Т дней удержания актива;
, - рыночная цена актива в момент времени t и
t-Т.
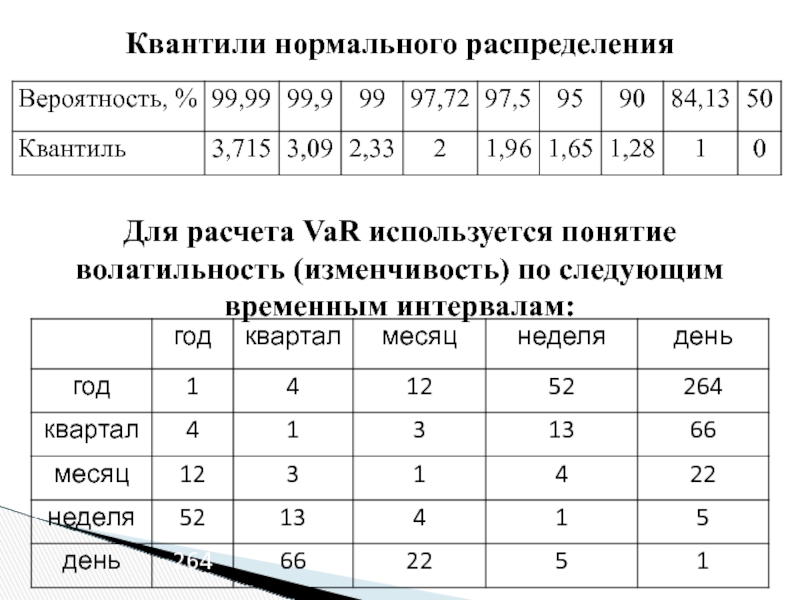
Слайд 18Квантили нормального распределения
Для расчета VaR используется понятие волатильность (изменчивость) по следующим
Слайд 20- сравнительная простота реализации;
- сравнительно небольшие затраты на сбор первичных данных
- приемлемая точность в большинстве случаев практического применения.
Достоинства ДНМ:
Слайд 21- низкая точность оценки риска нелинейных инструментов, таких как опционы. Он
- из-за отклонения на краях распределения плотности вероятностей от нормального распределения оценки VaR, рассчитанные на основе нормального распределения, оказываются заниженными или завышенными (в зависимости от величины уровня доверия);
- игнорирование риска одиночных событий, приводящих к аномальным убыткам и не происходящих достаточно часто, чтобы быть представленными в последних исторических данных.
Недостатки ДНМ:
Слайд 22Относится к группе методов полного оценивания и является непараметрическим. Он основан
Сначала выбирается период времени глубины Т (например, 200 торговых дней), за который отслеживаются исторические изменения (например, дневные) цен Р всех N входящих в портфель активов:
Метод исторического моделирования
Слайд 23 Для каждого из этих Т сценариев изменений моделируется гипотетическая цена
Затем производится полная переоценка всего текущего портфеля по ценам, смоделированным на основе исторических сценариев, и для каждого сценария вычисляется, насколько изменилась бы стоимость портфеля:
Слайд 24 После этого полученные Т изменений портфеля ранжируются по убыванию (от самого
Слайд 25- Отсутствие предположений о нормальном распределении доходностей факторов риска или какой-либо
- Хорошая точность оценки риска нелинейных инструментов;
- Простота полной переоценки портфеля, осуществляемой по историческим сценариям;
- Отсутствие риска использования ошибочной модели для оценки стоимости инструментов;
- Интуитивная простота и наглядность.
Достоинства МИМ:
Слайд 26- Использование только одной траектории эволюции цен;
- Несоблюдение в реальности базовой
- Высокая вероятность ошибок измерения при малой глубине исторической ретроспективы;
- Игнорирование различий между старыми и последними наблюдениями, тогда как удаление из выборки наиболее старых наблюдений может резко улучшить точность модели;
- Большой объем вычислений для крупных диверсифицированных портфелей при том, что агрегирование (например, использование одной дельты для различных инструментов) может снизить преимущества полного оценивания.
Недостатки МИМ:
Слайд 29 Моделирование случайных процессов (траектории цен) с заданными характеристиками. В отличие от
Метод Монте-Карло
Слайд 30 Траектория цен – это последовательность псевдослучайным образом смоделированных цен, начиная от
Затем производится полная переоценка портфеля по цене последнего шага и расчет изменения его стоимости для каждого сценария. Оценка VaR производится по распределению изменений стоимости портфеля.
Генерация случайных чисел в методе Монте-Карло состоит из двух шагов. Сначала можно воспользоваться генератором случайных чисел, равномерно распределенных на интервале между О и 1. Затем, используя как аргументы полученные случайные числа, вычисляют значения функций моделируемых распределений.
Слайд 31 Существует вариант метода Монте-Карло, при котором для моделирования цен используются непосредственные
Слайд 32- Высокая точность расчетов;
- Высокая точность применительно к инструментам с нелинейными
- Возможность моделирования любых исторических и гипотетических распределений, учет эффекта «толстых хвостов» и скачков цен.
Достоинства метода Монте-Карло
Слайд 33- Высокая сложность моделей и соответственно высокий риск неадекватности моделей;
- Высокие
Недостатки метода Монте-Карло