- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производные процентные расчеты презентация
Содержание
- 1. Производные процентные расчеты
- 2. Средние процентные ставки Если в финансовой
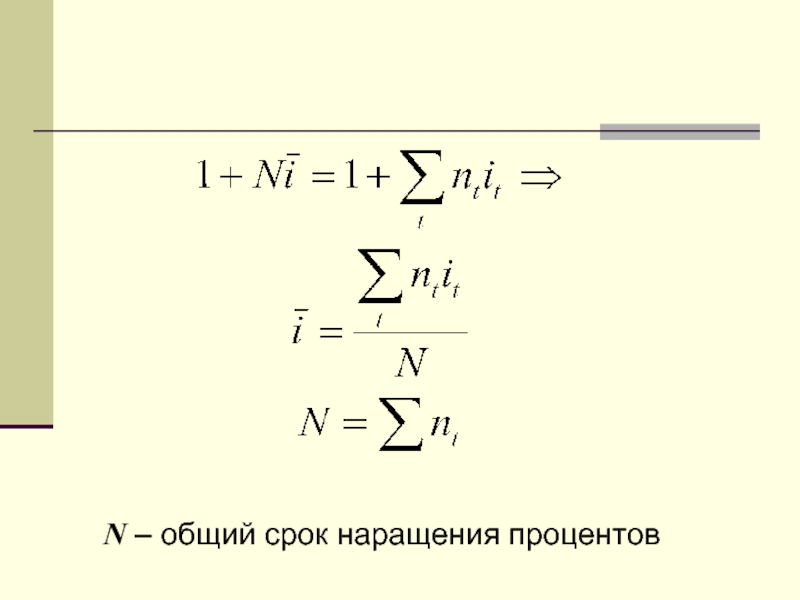
- 3. N – общий срок наращения процентов
- 4. Сложные переменные во времени ставки сложных процентов
- 5. Усреднение ставок, применяемых в нескольких однородных
- 6. Усреднение сложных ставок для однородных ссудных
- 7. Финансовая эквивалентность обязательств Эквивалентными считаются такие платежи,
- 8. Консолидирование (объединение) задолженности Для краткосрочных обязательств приведение
- 9. Пусть платежи S1, S2,…Sm
- 10. Определение размера консолидированного платежа Пусть n1< n2 n0
- 11. Определение срока консолидированного платежа Если при объединении
- 12. При применении простой ставки получим При применении сложной ставки получим
- 13. Налоги При начислении простых процентов за весь
- 14. Инфляция Введем обозначения: S - наращенная сумма
- 15. Очевидно, что Sα = S
- 16. Под темпом инфляции h понимается относительный
- 17. Инфляция является цепным процессом. Следовательно, индекс
- 18. Если h - постоянный ожидаемый (или
- 19. Если наращение производится по простой ставке,
- 20. Если наращение производится по сложным процентам, то наращенная сумма с учетом покупательной способности равна
- 21. Определим брутто-ставку r при условии полной
Слайд 2Средние процентные ставки
Если в финансовой операции размер процентной ставки изменяется
во времени, то все значения ставки можно обобщить с помощью средней.
Замена всех усредняемых значений ставок на среднюю процентную ставку не изменяет результатов наращения или дисконтирования.
Замена всех усредняемых значений ставок на среднюю процентную ставку не изменяет результатов наращения или дисконтирования.
Слайд 5
Усреднение ставок, применяемых в нескольких однородных операциях, которые различаются суммами ссуд
и процентными ставками
Слайд 7Финансовая эквивалентность обязательств
Эквивалентными считаются такие платежи, которые, будучи "приведенными" к одному
моменту времени оказываются равными.
Приведение осуществляется путем дисконтирования или наращения суммы платежа.
Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.
Приведение осуществляется путем дисконтирования или наращения суммы платежа.
Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить.
Слайд 8Консолидирование (объединение) задолженности
Для краткосрочных обязательств приведение осуществляется обычно на основе простых
ставок, для средне- и долгосрочных — с помощью сложных процентных ставок.
Одним из распространенных случаев изменения условий контрактов является консолидация (объединение) платежей.
Одним из распространенных случаев изменения условий контрактов является консолидация (объединение) платежей.
Слайд 9
Пусть платежи
S1, S2,…Sm
со сроками
n1, n2,…nm
заменяются одним в
сумме S0 и сроком n0.
В этом случае возможны две постановки задачи: если задается срок n0, то находится сумма S0 и наоборот, если задана сумма консолидированного платежа S0, то определяется срок n0.
Рассмотрим обе постановки задачи.
В этом случае возможны две постановки задачи: если задается срок n0, то находится сумма S0 и наоборот, если задана сумма консолидированного платежа S0, то определяется срок n0.
Рассмотрим обе постановки задачи.
Слайд 10Определение размера консолидированного платежа
Пусть n1< n2
при использовании простых процентных ставок получим
Sj – размеры объединяемых платежей со сроками nj < n0,
Sk – размеры платежей со сроками nk > n0
Sj – размеры объединяемых платежей со сроками nj < n0,
Sk – размеры платежей со сроками nk > n0
Слайд 11Определение срока консолидированного платежа
Если при объединении платежей задана величина консолидированного платежа
S0, то возникает проблема определения его срока n0. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей.
Слайд 13Налоги
При начислении простых процентов за весь срок:
При начислении сложных процентов за
весь срок:
Слайд 14Инфляция
Введем обозначения:
S - наращенная сумма денег, измеренная по номиналу,
Sα - наращенная
сумма с учетом ее обесценения,
Ip - индекс цен,
Iα - индекс, характеризующий изменение покупательной способности денег за период
h - темп инфляции
Ip - индекс цен,
Iα - индекс, характеризующий изменение покупательной способности денег за период
h - темп инфляции
Слайд 15
Очевидно, что
Sα = S Iα
Индекс покупательной способности денег равен обратной величине
индекса цен - чем выше цены, тем ниже покупательная способность:
Слайд 16
Под темпом инфляции h понимается относительный прирост цен за период, он
измеряется в процентах и равен
h = 100 (Iр - 1).
В свою очередь
h = 100 (Iр - 1).
В свою очередь
Слайд 17
Инфляция является цепным процессом. Следовательно, индекс цен за несколько периодов равен
произведению цепных индексов цен:
где ht — темп инфляции в периоде t
где ht — темп инфляции в периоде t
Слайд 18
Если h - постоянный ожидаемый (или прогнозируемый) темп инфляции за один
период, то за n таких периодов получим
Слайд 19
Если наращение производится по простой ставке, то наращенная сумма с учетом
покупательной способности равна
Увеличение наращенной суммы с учетом ее инфляционного обесценения имеет место только тогда, когда 1 + in > Ip
Увеличение наращенной суммы с учетом ее инфляционного обесценения имеет место только тогда, когда 1 + in > Ip
Слайд 20
Если наращение производится по сложным процентам, то наращенная сумма с учетом
покупательной способности равна
Слайд 21
Определим брутто-ставку r при условии полной компенсации инфляции. При наращении по
сложной процентной ставке: