- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Futures and Forwards презентация
Содержание
- 1. Futures and Forwards
- 2. 19- Forward – a deferred-delivery sale of
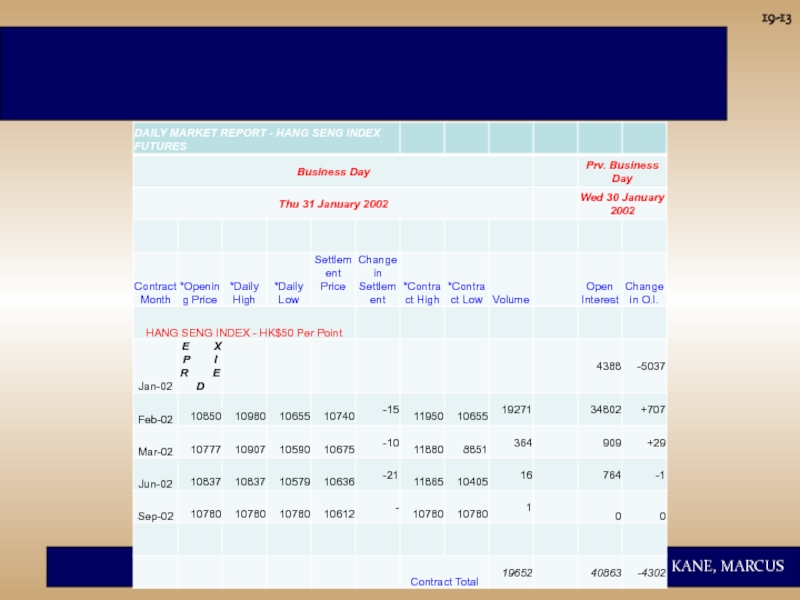
- 3. 19-
- 4. 19-
- 5. 19-
- 6. 19-
- 7. 19-
- 8. 19-
- 9. 19-
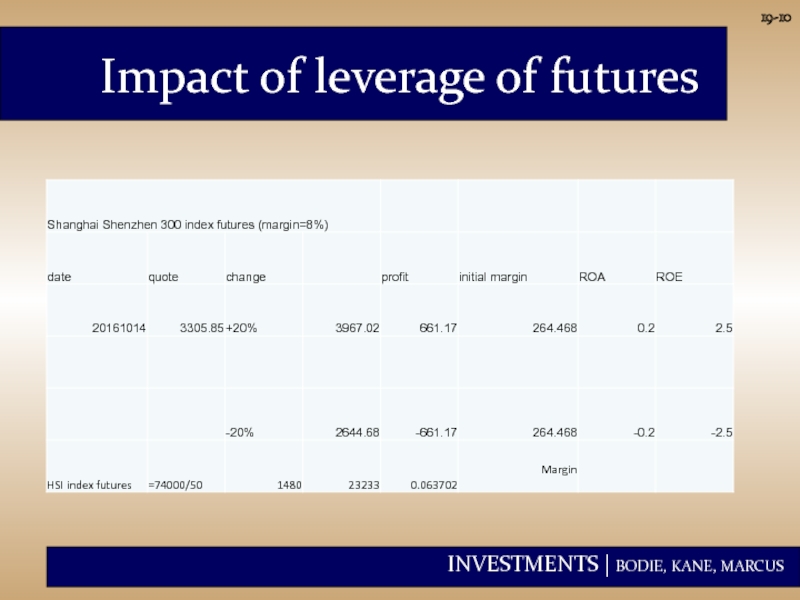
- 10. Impact of leverage of futures 19-
- 11. 19- A futures contract is the obligation
- 12. 19-
- 13. 19-
- 14. Shanghai Shenzhen 300 index futures 19-
- 15. Dalian commodity exchange 19-
- 16. 19- Basics of Futures Contracts Long –
- 17. 19- Basics of Futures Contracts Profit to
- 18. 19- Figure 19.2 Profits to Buyers and Sellers of Futures and Option Contracts
- 19. 19- Figure 19.2 Conclusions Profit is zero
- 20. 19- Existing Contracts Futures contracts are traded
- 21. 19- Trading Mechanics Electronic trading has mostly
- 22. 19- Open interest is the number of
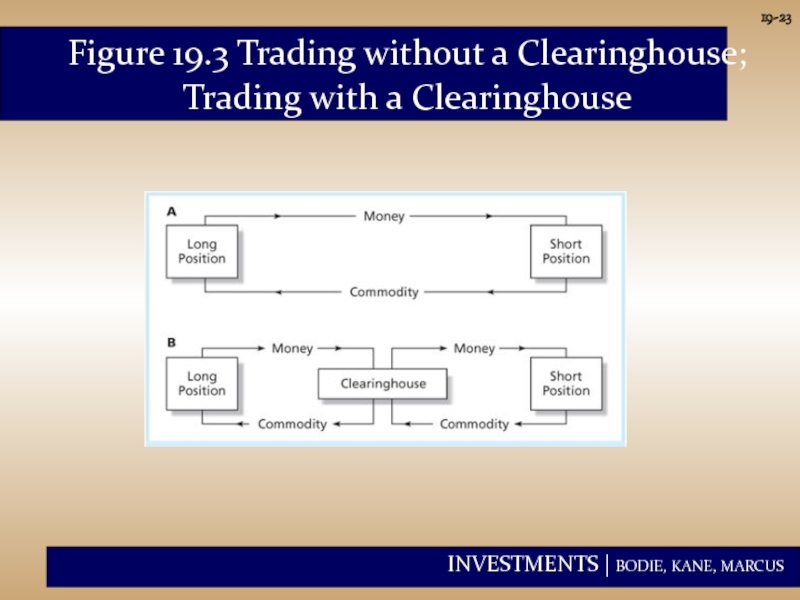
- 23. 19- Figure 19.3 Trading without a Clearinghouse; Trading with a Clearinghouse
- 24. 19- Marking to Market - each day
- 25. 19- Initial Margin - funds or interest-earning
- 26. 19- Trading Strategies Speculators seek to profit
- 27. 19- Basis - the difference between the
- 28. 19- Before maturity, FT may differ substantially
- 29. 19- Spot-futures parity theorem - two ways
- 30. 19- Spot-Futures Parity Theorem With a perfect
- 31. 19- Hedge Example: Section 19.4 Investor holds
- 32. 19- Hedge Example Outcomes Value of ST
- 33. 19- Rate of Return for the Hedge
- 34. 19- The Spot-Futures Parity Theorem Rearranging terms
- 35. 19- Arbitrage Possibilities If spot-futures parity
- 36. 19- Spread Pricing: Parity for Spreads
- 37. 19- Spreads If the risk-free rate is
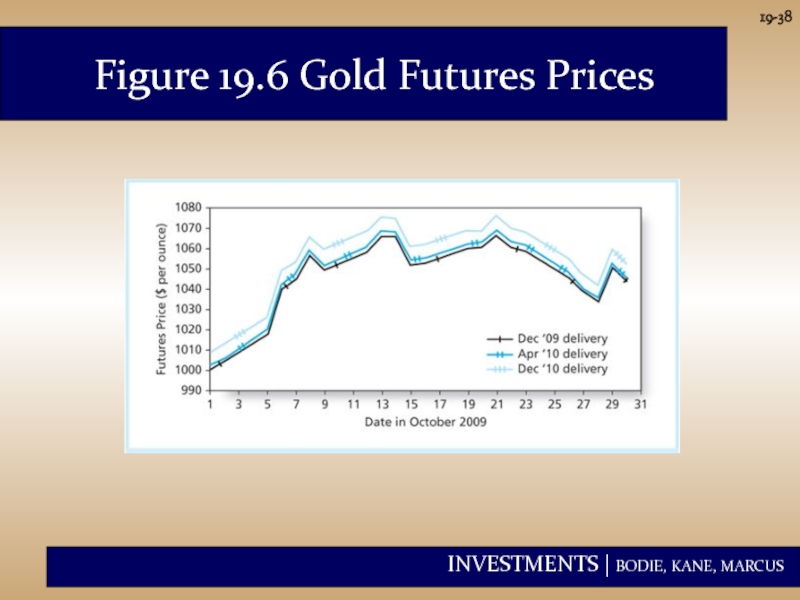
- 38. 19- Figure 19.6 Gold Futures Prices
- 39. 19- Futures Prices vs. Expected Spot Prices
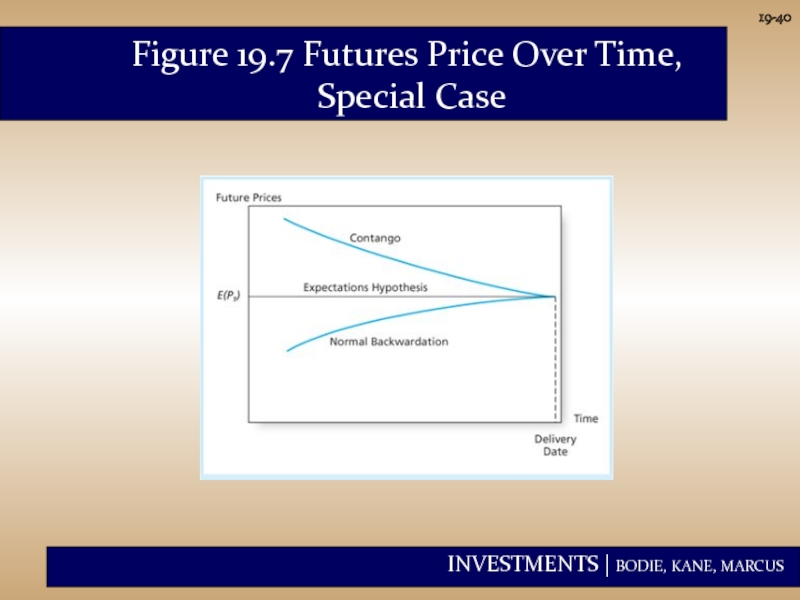
- 40. 19- Figure 19.7 Futures Price Over Time, Special Case
19- Forward – a deferred-delivery sale of an asset with the sales price agreed on now. Futures - similar to forward but feature formalized and standardized contracts. Key difference in futures
Слайд 219-
Forward – a deferred-delivery sale of an asset with the sales
price agreed on now.
Futures - similar to forward but feature formalized and standardized contracts.
Key difference in futures
Standardized contracts create liquidity
Marked to market
Exchange mitigates credit risk
Ex next page
Futures - similar to forward but feature formalized and standardized contracts.
Key difference in futures
Standardized contracts create liquidity
Marked to market
Exchange mitigates credit risk
Ex next page
Futures and Forwards
Слайд 1119-
A futures contract is the obligation to make or take delivery
of the underlying asset at a predetermined price. Shanghai Shenzhen 300 index futures next 2 pages
Futures price – the price for the underlying asset is determined today, but settlement is on a future date.
The futures contract specifies the quantity and quality of the underlying asset and how it will be delivered.
Futures price – the price for the underlying asset is determined today, but settlement is on a future date.
The futures contract specifies the quantity and quality of the underlying asset and how it will be delivered.
Basics of Futures Contracts
Слайд 1619-
Basics of Futures Contracts
Long – a commitment to purchase the commodity
on the delivery date.
Short – a commitment to sell the commodity on the delivery date.
Futures are traded on margin.
At the time the contract is entered into, no money changes hands.
Short – a commitment to sell the commodity on the delivery date.
Futures are traded on margin.
At the time the contract is entered into, no money changes hands.
Слайд 1719-
Basics of Futures Contracts
Profit to long = Spot price at maturity
- Original futures price
Profit to short = Original futures price - Spot price at maturity
The futures contract is a zero-sum game, which means gains and losses net out to zero.
Profit to short = Original futures price - Spot price at maturity
The futures contract is a zero-sum game, which means gains and losses net out to zero.
Слайд 1919-
Figure 19.2 Conclusions
Profit is zero when the ultimate spot price, PT
equals the initial futures price, F0 .
Unlike a call option, the payoff to the long position can be negative because the futures trader cannot walk away from the contract if it is not profitable.
Unlike a call option, the payoff to the long position can be negative because the futures trader cannot walk away from the contract if it is not profitable.
Слайд 2019-
Existing Contracts
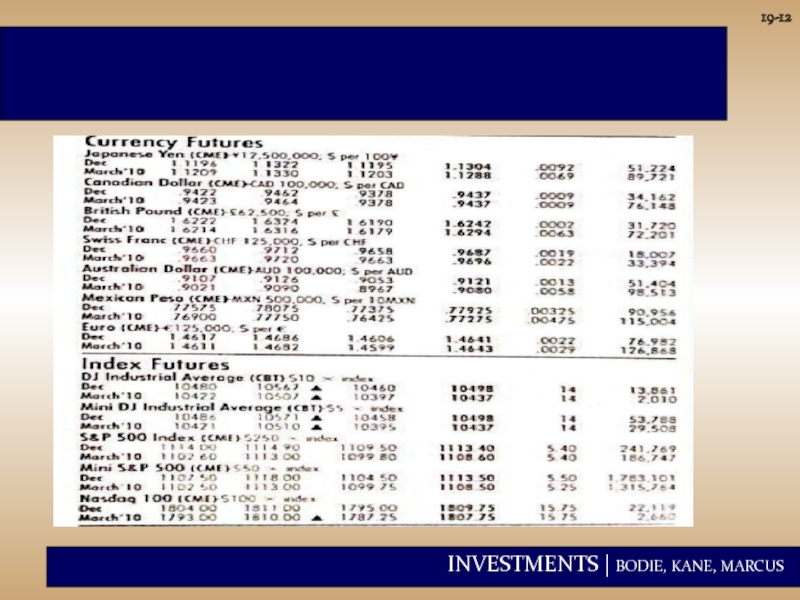
Futures contracts are traded on a wide variety of assets
in four main categories:
Agricultural commodities
Metals and minerals
Foreign currencies
Financial futures
Agricultural commodities
Metals and minerals
Foreign currencies
Financial futures
Слайд 2119-
Trading Mechanics
Electronic trading has mostly displaced floor trading.
CBOT and CME merged
in 2007 to form CME Group.
The exchange acts as a clearing house and counterparty to both sides of the trade.
The net position of the clearing house is zero.
Слайд 2219-
Open interest is the number of contracts outstanding.
If you are currently
long, you simply instruct your broker to enter the short side of a contract to close out your position.
Most futures contracts are closed out by reversing trades.
Only 1-3% of contracts result in actual delivery of the underlying commodity.
Most futures contracts are closed out by reversing trades.
Only 1-3% of contracts result in actual delivery of the underlying commodity.
Trading Mechanics
Слайд 2419-
Marking to Market - each day the profits or losses from
the new futures price are paid over or subtracted from the account
Convergence of Price - as maturity approaches the spot and futures price converge
Convergence of Price - as maturity approaches the spot and futures price converge
Margin and Marking to Market
Слайд 2519-
Initial Margin - funds or interest-earning securities deposited to provide capital
to absorb losses
Maintenance margin - an established value below which a trader’s margin may not fall
Margin call - when the maintenance margin is reached, broker will ask for additional margin funds
Maintenance margin - an established value below which a trader’s margin may not fall
Margin call - when the maintenance margin is reached, broker will ask for additional margin funds
Margin and Trading Arrangements
Слайд 2619-
Trading Strategies
Speculators
seek to profit from price movement
short - believe price will
fall
long - believe price will rise
long - believe price will rise
Hedgers
seek protection from price movement
long hedge - protecting against a rise in purchase price
short hedge - protecting against a fall in selling price
Слайд 2719-
Basis - the difference between the futures price and the spot
price, FT – PT
The convergence property says FT – PT= 0 at maturity.
The convergence property says FT – PT= 0 at maturity.
Basis and Basis Risk
Слайд 2819-
Before maturity, FT may differ substantially from the current spot price.
Basis
Risk - variability in the basis means that gains and losses on the contract and the asset may not perfectly offset if liquidated before maturity.
Basis and Basis Risk
Слайд 2919-
Spot-futures parity theorem - two ways to acquire an asset for
some date in the future:
Purchase it now and store it
Take a long position in futures
These two strategies must have the same market determined costs
Purchase it now and store it
Take a long position in futures
These two strategies must have the same market determined costs
Futures Pricing
Слайд 3019-
Spot-Futures Parity Theorem
With a perfect hedge, the futures payoff is certain
-- there is no risk.
A perfect hedge should earn the riskless rate of return.
This relationship can be used to develop the futures pricing relationship.
A perfect hedge should earn the riskless rate of return.
This relationship can be used to develop the futures pricing relationship.
Слайд 3119-
Hedge Example: Section 19.4
Investor holds $1000 in a mutual fund indexed
to the S&P 500.
Assume dividends of $20 will be paid on the index fund at the end of the year.
A futures contract with delivery in one year is available for $1,010.
The investor hedges by selling or shorting one contract .
Assume dividends of $20 will be paid on the index fund at the end of the year.
A futures contract with delivery in one year is available for $1,010.
The investor hedges by selling or shorting one contract .
Слайд 3219-
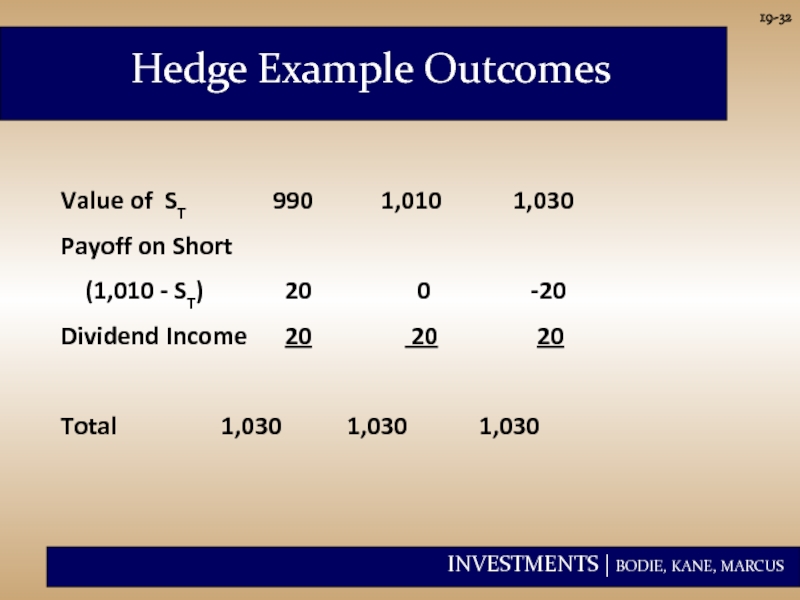
Hedge Example Outcomes
Value of ST 990 1,010 1,030
Payoff on Short
(1,010
- ST) 20 0 -20
Dividend Income 20 20 20
Total 1,030 1,030 1,030
Dividend Income 20 20 20
Total 1,030 1,030 1,030
Слайд 3519-
Arbitrage Possibilities
If spot-futures parity is not observed, then arbitrage is
possible.
If the futures price is too high, short the futures and acquire the stock by borrowing the money at the risk free rate.
If the futures price is too low, go long futures, short the stock and invest the proceeds at the risk free rate.
If the futures price is too high, short the futures and acquire the stock by borrowing the money at the risk free rate.
If the futures price is too low, go long futures, short the stock and invest the proceeds at the risk free rate.
Слайд 3719-
Spreads
If the risk-free rate is greater than the dividend yield (rf
> d), then the futures price will be higher on longer maturity contracts.
If rf < d, longer maturity futures prices will be lower.
For futures contracts on commodities that pay no dividend, d=0, F must increase as time to maturity increases.
If rf < d, longer maturity futures prices will be lower.
For futures contracts on commodities that pay no dividend, d=0, F must increase as time to maturity increases.
Слайд 3919-
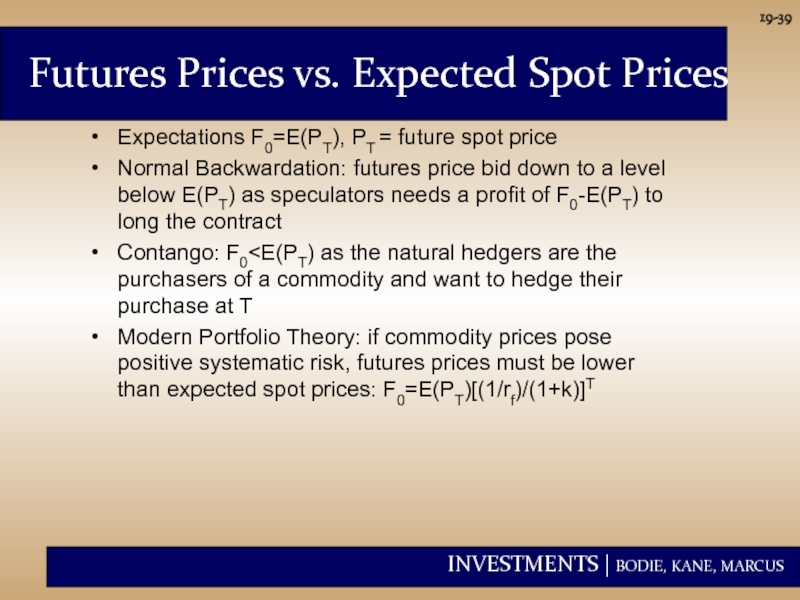
Futures Prices vs. Expected Spot Prices
Expectations F0=E(PT), PT = future spot
price
Normal Backwardation: futures price bid down to a level below E(PT) as speculators needs a profit of F0-E(PT) to long the contract
Contango: F0Modern Portfolio Theory: if commodity prices pose positive systematic risk, futures prices must be lower than expected spot prices: F0=E(PT)[(1/rf)/(1+k)]T
Normal Backwardation: futures price bid down to a level below E(PT) as speculators needs a profit of F0-E(PT) to long the contract
Contango: F0
