- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели ценообразования презентация
Содержание
- 1. Модели ценообразования
- 2. Модели ценообразования
- 3. Список литературы Брусов П.Н., Филатова Т.В., Лахметкина
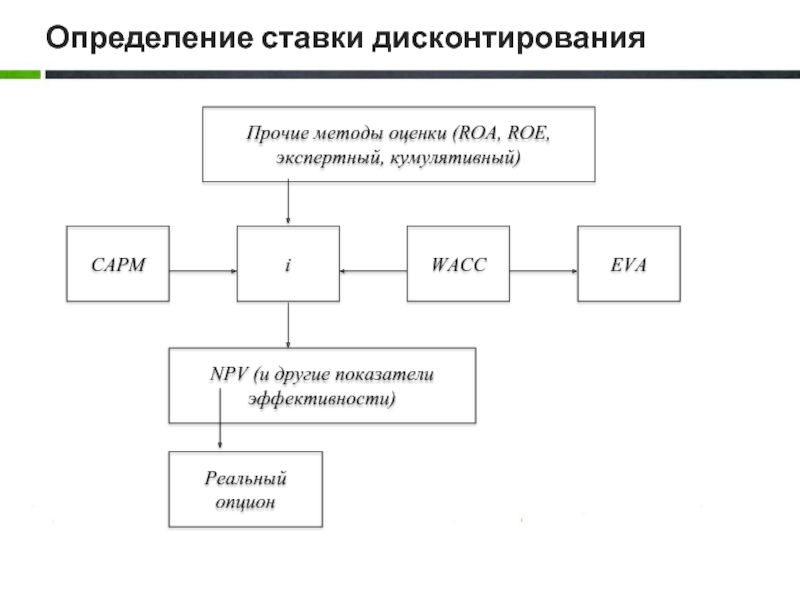
- 4. Определение ставки дисконтирования
- 6. CAPM Capital Asset Price Model модель ценообразования
- 7. У. Шарп (William Sharpe) – Нобелевская премия по экономике 1990
- 8. Модель оценки финансовых активов ожидаемый доход, который
- 9. Допущения модели CAPM Эффективный финансовый рынок, доступность
- 10. Следствия модели Модель на один период Нормальное
- 11. Систематический vs специфического риска Систематический (рыночный /
- 12. Модель ценообразования капитальных активов (CAPM) где Re
- 13. Систематический риск (β-коэффициент) Cov(ri, rm) – функции ковариации; Var (rm) – функция дисперсии;
- 14. β - риск β - совокупный риск
- 15. Модель CAPM для реальных проектов NPV
- 16. Пример 1 Пусть в рамках однопериодной экономики
- 17. Алгоритм решения Находим чистую доходность rx в
- 19. Пример 2 Текущая рыночная доходность rm =16%,
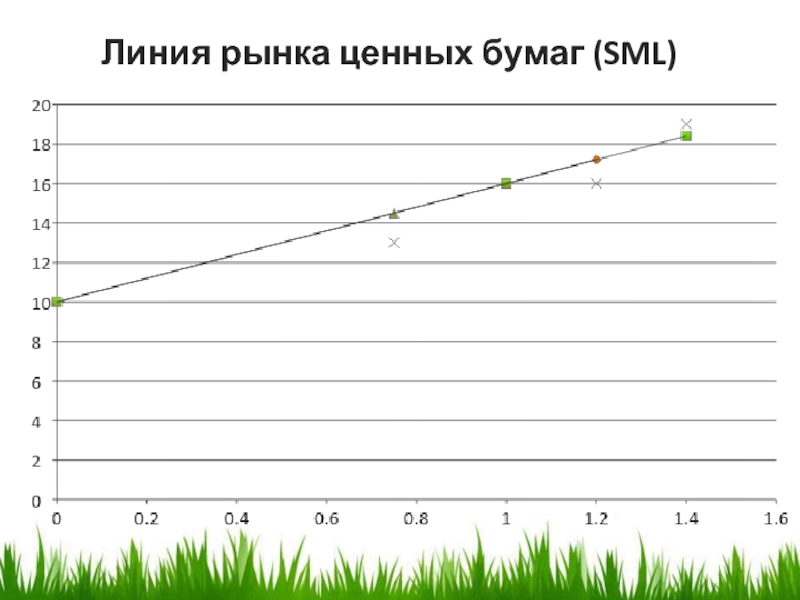
- 20. Линия рынка ценных бумаг (SML)
- 21. Альтернативы модели CAPM Факторные модели (i =1,
- 22. Альтернативные CAPM модели 3) Модель Ольсона
- 24. EVA показатель экономической добавленной стоимости, определяемой как
- 25. Особенности организация рассматривается подобно инвестиционному проекту эффективность
- 27. Опцион - договор, в соответствии с которым
- 28. Развитие теории 1973 год Фишер Блэк
- 29. Опционный контракт Опцион кол (call) Опцион пут
- 31. Пример торговли опционами на МосБирже
- 32. Реальный опцион это право (и не
- 33. Виды реальных опционов Опцион на выбор времени
- 34. Методы оценки реальных опционов Модель Блека-Шоулза
- 35. Модель Блэка-Шоулза
- 36. Цена опциона колл Цена опциона пут
- 38. Волатильность стандартное отклонение цены от среднего
- 39. Пример 1 S0 - цена базового актива
- 40. Решение d1=[ln(S0/X)+(r+0.5σ2)T]/σ√T =[ln(100/200)+(0.05+0.5∗0.32)3]/(0.3∗ √3) =0.119 d2=
- 41. Модель Блека-Шоулза для оценки реальных опционов где
- 42. Цена реального опциона тем выше, чем:
- 43. Пример 2 Предприятие собирается ввести в действие
- 44. Решение Определим NPV при i=15% NPV =
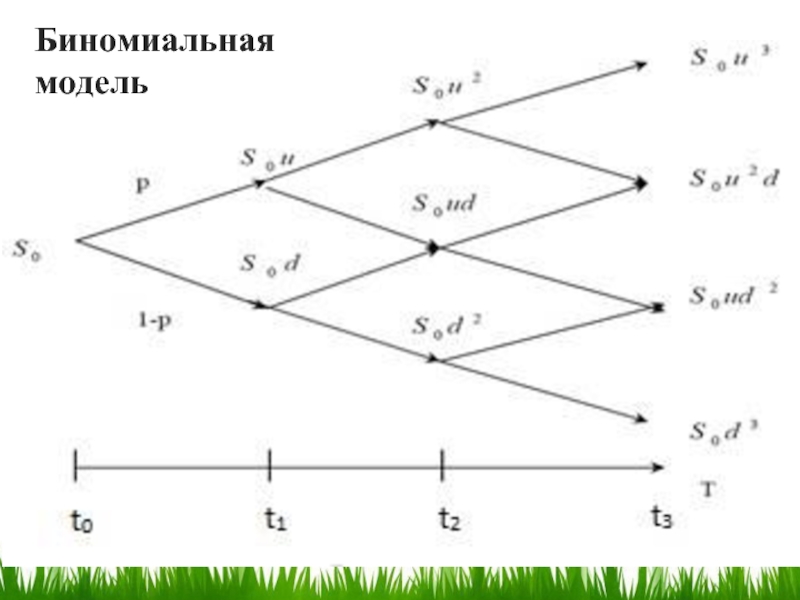
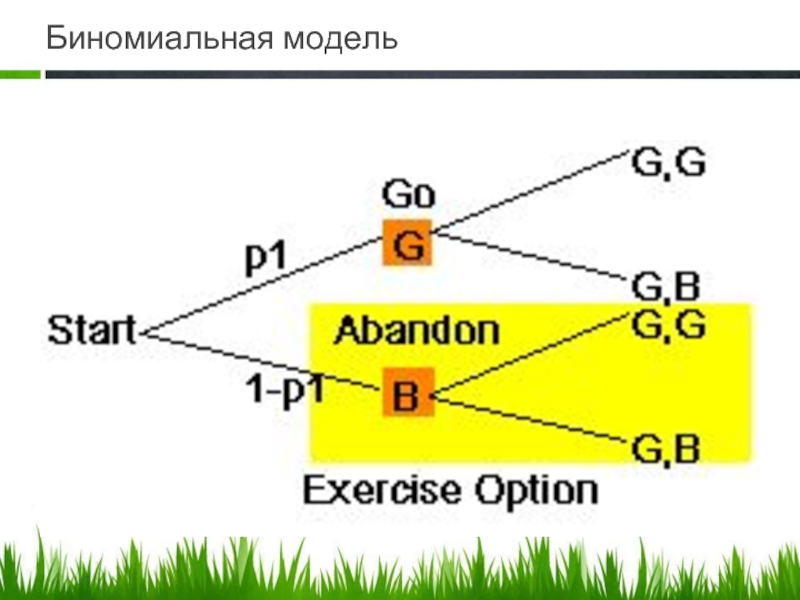
- 45.  Биномиальная модель
- 46. Биномиальная модель
- 47. Пример 3 Стоимость компании без долговых обязательств
- 48. Решение d1=
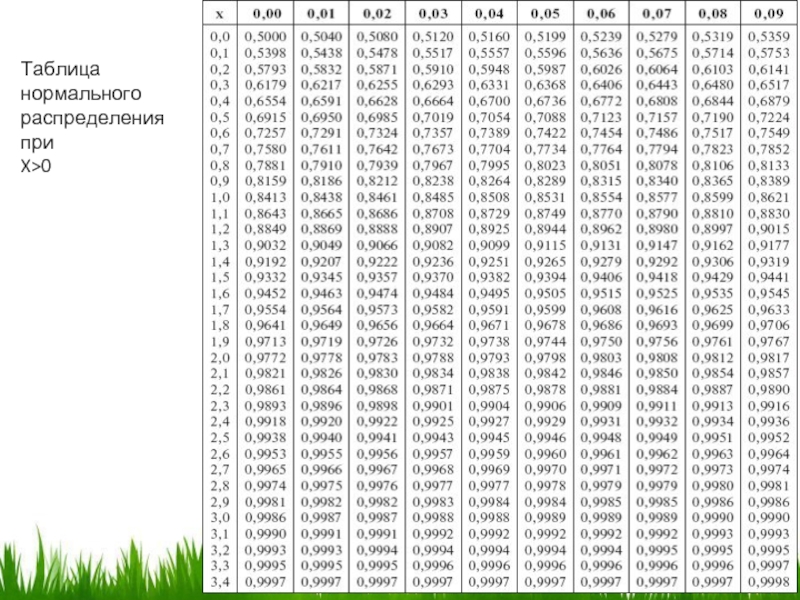
- 49. Таблица нормального распределения при X>0
- 50. Таблица нормального распределения при X
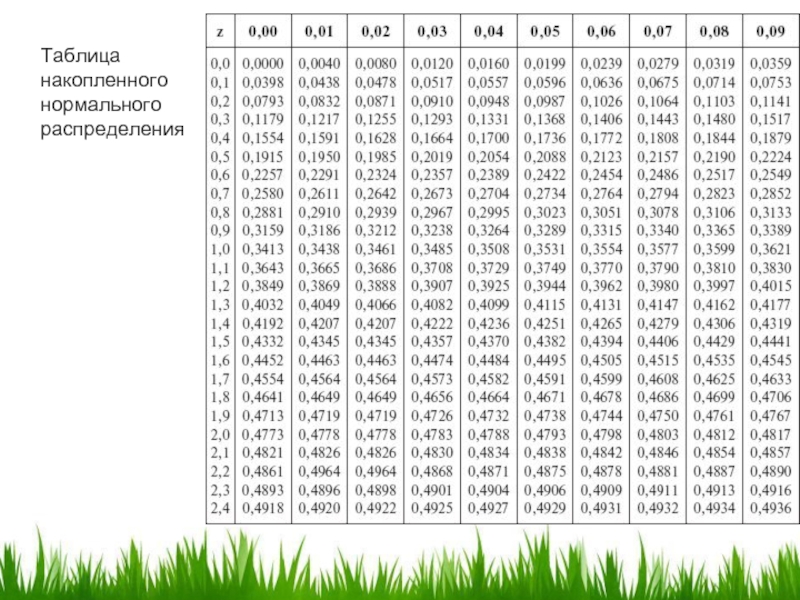
- 51. Таблица накопленного нормального распределения
- 53. Опцион на покупку акций, по которым выплачиваются
Слайд 1Пример 2
Стоимость компании без долговых обязательств V=10 млн.
Компания собирается эмитировать
F=7 млн. со сроком погашения через T=10 лет.
Стандартное отклонение доходности компании σ=0,6324, безрисковая ставка - 10% (r=0,1).
Определить стоимость собственного капитала компании.
Слайд 3Список литературы
Брусов П.Н., Филатова Т.В., Лахметкина Н.И. Инвестиционный менеджмент: Учебник, М.:
Хамедшин Д.Р. К вопросу об использовании моделей ценообразования активов в анализе эффективности реальных инвестиций // Российский экономический интернет-журнал [Электронный ресурс]. – М.: АТиСО, 2009. – Режим доступа: http://www.e-rej.ru/Articles/2009/Khametshin.pdf
Сысоев А. Ю. Использование моделей «реальных опционов» при оценке эффективности инвстиционных проектов // ВЕСТНИК ФА, 2003, - №4. – 110-120
Слайд 6CAPM
Capital Asset Price Model
модель ценообразования финансовых активов
1
Модель основана на портфельной
Основоположники:
У. Шарп, Дж. Линтер, Я. Моссин, Дж.Трейнер
Слайд 8Модель оценки финансовых активов
ожидаемый доход, который потребуют инвесторы, равен ставке по
Если ожидаемый риск не равен или выше, чем требуемая доходность, то инвесторы откажутся инвестировать, и инвестиции не будут сделаны.
Выделены систематический и специфический риск.
Слайд 9Допущения модели CAPM
Эффективный финансовый рынок, доступность информации, рациональное поведение инвесторов
Отсутствие транзакционных
Стремление инвесторов к максимизации ожидаемой доходности при минимизации рисков
Одинаковый период вложения для инвесторов
Делимость и ликвидность финансовых инструментов
Несущественные налоги и операционные издержки
Кредитование и заимствования по безрисковой ставке при возможности рисковых инвестиций
Одинаковая безрисковая ставка для всех инвесторов
Слайд 10Следствия модели
Модель на один период
Нормальное распределение Гаусса
Отсутствие человеческого капитала (т.к. он
Инвестиции в индивидуальные ценные бумаги бесполезно; формирование портфелей из дешевых индексных фондов
Слайд 11Систематический vs специфического риска
Систематический (рыночный / недиверсифицируемый) риск – это риск,
Специфический (несистематический) риск – риск, являющийся результатом состояния отдельной отрасли, предприятия, типа инвестиционного процента. Связан с внутренними факторами деятельности эмитента акций или инвестора, отрицательно воздействующими на эффективность инвестирования. Может быть устранен диверсификацией.
Слайд 12Модель ценообразования капитальных активов (CAPM)
где Re – ожидаемая доходность на актив
Rf – безрисковая составляющая доходности;
Rm - ожидаемая средняя доходность рыночного портфеля (индекса);
β-коэффициент чувствительности ценной бумаги к изменению средней доходности портфеля (индекса).
Слайд 13Систематический риск (β-коэффициент)
Cov(ri, rm) – функции ковариации; Var (rm) – функция
Слайд 14β - риск
β - совокупный риск от инвестирования в общий рынок:
β компании - риск компании по сравнению с риском общего рынка. Beta показывает волатильность ценной бумаги, относительно типа актива. Если компания имеет Beta 3.0, то предполагается, что ее активы в 3 раза более рискованны, чем общий рынок.
Слайд 15Модель CAPM для реальных проектов
NPV = P(X) – I
P(X) –
I – инвестиционные затраты нулевого периода.
X – ожидаемый будущий доход; rx – ожидаемая доходность от инвестиций с аналогичным уровнем риска.
Слайд 16Пример 1
Пусть в рамках однопериодной экономики неопределенность характеризуется двумя потенциальными состояниями:
Вероятность реализации событий:
π(u)=0,7 и π (d)=0,3.
Случайная доходность рыночного портфеля задана следующим распределением:
rm(u) =15% и rm(d)=3%.
rf = 5% (безрисковая ставка);
I = 70 тыс. руб.
X(u) = 100 тыс. руб.; X(d) = 80 тыс. руб.
Оценить инвестиционную привлекательность проекта с помощью критерия NPV.
Слайд 17Алгоритм решения
Находим чистую доходность rx в каждом будущем моменте времени.
Оценим ожидаемую
Рассчитаем ожидаемый доход проекта X и его NPV.
Слайд 19Пример 2
Текущая рыночная доходность rm =16%, а безрисковая ставка rf =10%.
Вопрос:
а) Какие из акций являются переоцененными согласно САРМ?
б) Какие из акций являются недооцененными согласно САРМ?
в) Постройте линию рынка ценных бумаг.
Слайд 21Альтернативы модели CAPM
Факторные модели (i =1, 2, 3…, n)
Теория арбитражного ценообразования
Основное предположение: каждый инвестор стремится увеличить доходность портфеля без увеличения риска
Возможные факторы: индекс промышленного производства, инфляция, краткосрочная реальная ставка процентов, риск неуплаты по облигациям
Слайд 22Альтернативные CAPM модели
3) Модель Ольсона (EBO - Edwards-Bell-Ohlson valuation model)
Стоимость
E – ожидаемые значения;
ROE – рентабельность акционерного капитала;
Bt – стоимость чистых активов (балансовая стоимость)
re – цена акционерного капитала
Слайд 23
2
EVA
Economic Value Added
Экономическая добавленная стоимость
Разработан
Д. Стерном и Б. Стюартом
Слайд 24EVA
показатель экономической добавленной стоимости, определяемой как разница между чистой операционной прибылью
где NOPAT – чистая операционная прибыль после уплаты налогов;
IC – объем инвестированного капитала;
WACC – средневзвешенная стоимость капитала;
ROIC – рентабельность инвестированного капитала.
Слайд 25Особенности
организация рассматривается подобно инвестиционному проекту
эффективность инвестиций подтверждается приростом стоимости организации (неотрицательный
Простота формулы
применение корректировок капитала, позволяющих сделать прибыль организации ближе к денежному потоку, а капитал выразить корректней.
Слайд 27Опцион
- договор, в соответствии с которым один из его участников приобретает
Слайд 28Развитие теории
1973 год
Фишер Блэк (Fisher Black), Майрон Шоулз (Myron Scholes)
1984 год
Стюарт Майерс (Stewart Myers) и Карл Кестер (Carl Kester)
Метод реальных опционов
Слайд 29Опционный контракт
Опцион кол (call)
Опцион пут (put)
Покупатель (держатель опциона) - long
Продавец
Слайд 32Реальный опцион
это право (и не обязанность) принять какое-либо управленческое решение в
Слайд 33Виды реальных опционов
Опцион на выбор времени принятия решения об осуществлении капитальных
Опцион роста - дополнительные возможности, которые могут появиться после того как сделаны первоначальные инвестиции.
Опцион изменения масштаба - увеличение или сокращение масштабов производства в течение жизненного цикла проекта.
Опцион на отказ от реализации проекта - отказ от наиболее нерентабельных проектов.
Слайд 34Методы оценки реальных опционов
Модель Блека-Шоулза
Black–Scholes Option Pricing Model (OPM)
Биномиальная модель
Д.Кокс,
Слайд 35Модель Блэка-Шоулза
S – рыночная цена базового актива;
Х – цена исполнения (цена актива по договору);
N(d1), N(d2) – вероятность того, что при нормальном распределении со средней, равной нулю, и стандартном отклонении, равном единице, результат будет меньше d1 и d2
r – безрисковая процентная ставка
t - срок контракта в днях
Слайд 36
Цена опциона колл
Цена опциона пут
S – рыночная цена базового актива;
Х –
N(d1), N(d2) – вероятность того, что при нормальном распределении со средней, равной нулю, и стандартном отклонении, равном единице, результат будет меньше d1 и d2
r – безрисковая процентная ставка
T-t - срок контракта
e=2,7183
Слайд 37
σ - стандартное отклонение цены акции, которое берется в годовом исчислении
Слайд 38Волатильность
стандартное отклонение цены от среднего
m - среднее значение случайной величины
n - число наблюдений;
хi - значение случайной величины в каждом наблюдении.
Слайд 39Пример 1
S0 - цена базового актива (текущая стоимость денежных потоков от
X –цена исполнения (размер инвестиций) – 250 млн. руб.
σ –волатильность (среднеквадратическое отклонение денежных потоков) – 30%
r – безрисковая ставка доходности (доходность государственных облигаций) – 5%
T – время истечения срока (длительность периода, на который может быть отложено принятие решения) – 3 года
N(d) – кумулятивная функция нормального распределения
Слайд 40Решение
d1=[ln(S0/X)+(r+0.5σ2)T]/σ√T =[ln(100/200)+(0.05+0.5∗0.32)3]/(0.3∗ √3) =0.119
d2= d1− σ√T = 0.119 − 0.3
N(d1) = 0.547
N(d2) =0.290
С=N(d1)S0−N(d2)? ∗exp-rT =0.547∗200−0.290∗ 250 ∗ exp−0.05 ∗ 3 = 47 млн. руб
Слайд 41Модель Блека-Шоулза для оценки реальных опционов
где C – рыночная цена опциона
S – курсовая стоимость базисного актива (текущая стоимость денежных потоков от инвестиций);
PV(х) – текущая стоимость цены исполнения опционного контракта, рассчитанная с применением краткосрочной безрисковой ставки доходности и срока исполнения опциона (приведенная стоимость инвестиций или ликвидационной стоимости в случае отказа от реализации проекта);
N(d1), N(d2) – вероятности, показывающие, что нормированная нормальная переменная d будет меньше d1 и d2 соответственно.
Слайд 42
Цена реального опциона тем выше, чем:
выше приведенная стоимость денежных потоков (S);
ниже
больше времени до истечения срока реализации опциона (t);
больше риск (σ).
Слайд 43Пример 2
Предприятие собирается ввести в действие линию по производству нового товара.
Начальные инвестиции – 110 млн. руб. необходимы для завершения подготовительной стадии проекта, которая длится год.
Еще 100 млн. руб. необходимо инвестировать через год - в момент начала производства.
Ожидается, что денежные потоки от продажи нового товара поступят в распоряжение предприятия к концу второго года с начала проекта. Однако в настоящее время трудно определить, будет ли новый продукт пользоваться спросом.
Вероятность позитивного развития событий (ожидаемый доход составит 340 млн. руб.) составляет 75%, а негативного (предполагаемый доход - 10 млн. руб.) - 25%.
Слайд 44Решение
Определим NPV при i=15%
NPV = (–110) + (–100) : 1,15 +
Предположим, что через год станет понятно, будет ли товар пользоваться спросом. Тогда менеджер будет иметь возможность отказаться от проекта в случае низкого спроса.
Возможность выбора – реальный опцион.
NPV = –110 + 0,75 × (-100) : 1,15 + (0,75 × 340 + 0,25 × 0) : 1,152 = 17,6
Слайд 47Пример 3
Стоимость компании без долговых обязательств S=10 млн. Компания собирается эмитировать
Определить стоимость собственного капитала компании.
Слайд 48Решение
d1=
ln1.4286=0.3577
d2= d1 – σT1/2 = 1,6788 - 0,6324*101/2 = - 0,321
N (-d1) = 0,0465; N (-d2) =0,1255
(см. таблица нормального распределения)
С= 7* 2,7183-0,1*10*0, 1255+10*0,0465 = 0,7897 млн руб
стоимость собственного капитала компании.
Слайд 53Опцион на покупку акций, по которым выплачиваются дивиденды.
Текущая стоимость = $
Если вы отложите инвестиции, то потеряете денежный поток первого года ($ 16 млн или $ 25 млн), но зато сможете избежать большой ошибки — инвестиций в размере $ 180 млн в проект, стоимость которого в будущем может составить всего $ 160 млн.
Опцион на покупку (колл-опцион). Стоимость при благоприятном исходе составит $ 70 млн в следующем году; при неблагоприятном — 0; сегодня опцион на покупку стоит $ 22,9 млн, что превышает выигрыш от его немедленной реализации в размере $ 20 млн.




































![Решениеd1=[ln(S0/X)+(r+0.5σ2)T]/σ√T =[ln(100/200)+(0.05+0.5∗0.32)3]/(0.3∗ √3) =0.119 d2= d1− σ√T = 0.119 − 0.3 ∗ √3 = −0.551](/img/tmb/2/198703/d94350499a39a2b8a236113a5c4002be-800x.jpg)