- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Умозаключение. Структура умозаключения презентация
Содержание
- 1. Умозаключение. Структура умозаключения
- 2. Структура умозаключения: Все киты млекопитающие
- 3. Виды умозаключений
- 4. Непосредственные умозаключения Превращение (метаморфоза) – меняется СВЯЗКА
- 5. Способы превращения: Двойное отрицание: утвердительные суждения
- 6. Обращение (перемещение) – в заключении субъект
- 7. Противопоставление предикату Вместо P берем не-P
- 8. A →E:
- 9. Непосредственные умозаключения Умозаключения по логическому квадрату
- 10. Умозаключения по логическому квадрату Отношения противоречия: А
- 11. Умозаключения по логическому квадрату Отношения частичной совместимости:
- 12. Опосредованные умозаключения. 1.Дедукция – из общего
- 13. Дедуктивное умозаключение Дедуктивное умозаключение – из двух
- 14. Простой категорический силлогизм (ПКС) Структура ПКС: Все
- 15. Простой категорический силлогизм (ПКС) Простой
- 16. Фигуры ПКС Фигура силлогизма
- 17. Модусы ПКС Модус ПКС – набор символов
- 18. Правила ПКС Для получения истинного заключения необходимо
- 19. Правила терминов ПКС 1. В ПКС должно
- 20. Правила посылок ПКС 1. Хотя бы одна
- 21. Сильные модусы ПКС Сильные = необходимые, правильные
Слайд 2Структура умозаключения:
Все киты млекопитающие
→ посылка
Все млекопитающие теплокровны → посылка
→ вывод
Все киты теплокровны → заключение
Вывод часто фиксируется понятиями «следовательно», «значит», «тогда», «таким образом»
Все млекопитающие теплокровны → посылка
→ вывод
Все киты теплокровны → заключение
Вывод часто фиксируется понятиями «следовательно», «значит», «тогда», «таким образом»
Слайд 4Непосредственные умозаключения
Превращение (метаморфоза) – меняется СВЯЗКА на противоположную, КВАНТОР остается тем
же
I→О
О→I
А→E
Е→A
I→О
О→I
А→E
Е→A
Слайд 5Способы превращения:
Двойное отрицание:
утвердительные суждения → в отрицательные:
[S есть P]
→ [S не есть не-P].
2 Перенос отрицания из связки в предикат: отрицательные суждения → в утвердительные
[S не есть P] → [S есть не-P]
2 Перенос отрицания из связки в предикат: отрицательные суждения → в утвердительные
[S не есть P] → [S есть не-P]
Слайд 6
Обращение (перемещение) – в заключении субъект и предикат меняются местами.
Простое:
А→А, Е→Е, I→I.
Обращение с ограничением: А→I, I→А.
Суждения О не подлежат обращению!
Обращение с ограничением: А→I, I→А.
Суждения О не подлежат обращению!
Слайд 7Противопоставление предикату
Вместо P берем не-P
Связку меняем на противоположную
Меняем
местами S и не-P
A→E
E→ I
O→I
Суждения I не подлежат противопоставлению предикату!!
A→E
E→ I
O→I
Суждения I не подлежат противопоставлению предикату!!
Слайд 8
A →E: [Все S есть
P] →
[Ни одно не-Р не есть S].
E→ I: [Ни одно S не есть P] →
[Некоторые не-Р есть S].
O→I: [Некоторые S не есть Р] →
[Некоторые не-Р есть S].
Суждения I не подлежат противопоставлению!
[Ни одно не-Р не есть S].
E→ I: [Ни одно S не есть P] →
[Некоторые не-Р есть S].
O→I: [Некоторые S не есть Р] →
[Некоторые не-Р есть S].
Суждения I не подлежат противопоставлению!
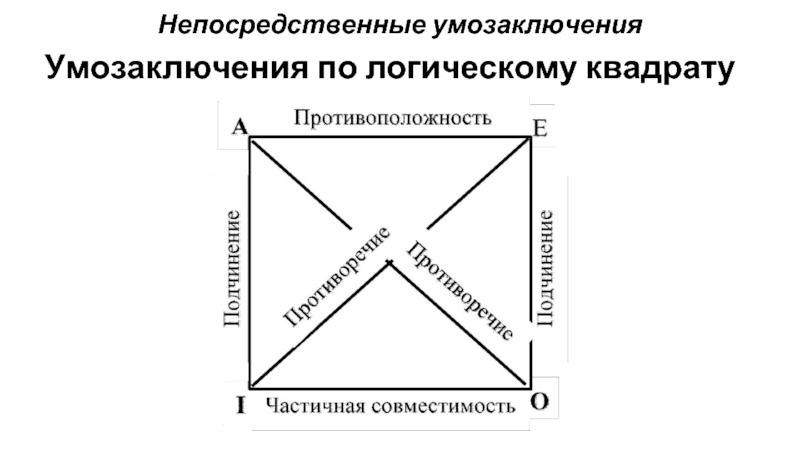
Слайд 10Умозаключения по логическому квадрату
Отношения противоречия:
А истинно ↔ О ложно, и наоборот
А
ложно ↔ О истинно, и наоборот
I истинно ↔ Е ложно, и наоборот
I ложно ↔ Е истинно, и наоборот
Отношения противоположности:
А истинно → Е ложно
Е истинно → А ложно
Но:
А ложно → Е может быть как ложным, так и истинным
Е ложно → А может быть как ложным, так и истинным
I истинно ↔ Е ложно, и наоборот
I ложно ↔ Е истинно, и наоборот
Отношения противоположности:
А истинно → Е ложно
Е истинно → А ложно
Но:
А ложно → Е может быть как ложным, так и истинным
Е ложно → А может быть как ложным, так и истинным
Слайд 11Умозаключения по логическому квадрату
Отношения частичной совместимости:
I ложно → О истинно
О ложно
→ I истинно
Но:
I истинно → О может быть как ложным, так и истинным
О истинно → I может быть как ложным, так и истинным
Отношения подчинения:
А истинно → I истинно
Е истинно → О истинно
I ложно → А ложно
О ложно → Е ложно
Но:
I истинно → А может быть как ложным, так и истинным
О истинно → Е может быть как ложным, так и истинным
ложно
А ложно → I может быть как ложным, так и истинным
истинно
Е ложно → О может быть как ложным, так и истинным
Но:
I истинно → О может быть как ложным, так и истинным
О истинно → I может быть как ложным, так и истинным
Отношения подчинения:
А истинно → I истинно
Е истинно → О истинно
I ложно → А ложно
О ложно → Е ложно
Но:
I истинно → А может быть как ложным, так и истинным
О истинно → Е может быть как ложным, так и истинным
ложно
А ложно → I может быть как ложным, так и истинным
истинно
Е ложно → О может быть как ложным, так и истинным
Слайд 12Опосредованные умозаключения.
1.Дедукция – из общего знания формируется общий вывод.
2.Индукция –
из частного знания формируется общий вывод
3. Аналогия – из частного знания формируется частный вывод.
3. Аналогия – из частного знания формируется частный вывод.
Слайд 13Дедуктивное умозаключение
Дедуктивное умозаключение – из двух суждений (одно из которых обязательно
общее!) необходимо вытекает единственный вывод.
Виды дедуктивных умозаключений:
1.Силлогизм - сначала идут посылки, а затем вывод.
Простой категорический силлогизм (ПКС) –из двух категорических суждений.
2.Доказательство - сначала идет вывод, а затем посылки.
Виды дедуктивных умозаключений:
1.Силлогизм - сначала идут посылки, а затем вывод.
Простой категорический силлогизм (ПКС) –из двух категорических суждений.
2.Доказательство - сначала идет вывод, а затем посылки.
Слайд 14Простой категорический силлогизм (ПКС)
Структура ПКС:
Все металлы [S] электропроводны [P].
М есть Р
Медь [S] есть металл [P]. S есть М
Медь [S] электропроводна [P]. S есть Р
Меньший термин ПКС = субъект заключения обозначается S. - «меньшая посылка»
Больший термин ПКС = предикат заключения, обозначается P. – «большая посылка»
Средний термин ПКС – входит в обе посылки и отсутствует в заключении, обозначается М.
Медь [S] есть металл [P]. S есть М
Медь [S] электропроводна [P]. S есть Р
Меньший термин ПКС = субъект заключения обозначается S. - «меньшая посылка»
Больший термин ПКС = предикат заключения, обозначается P. – «большая посылка»
Средний термин ПКС – входит в обе посылки и отсутствует в заключении, обозначается М.
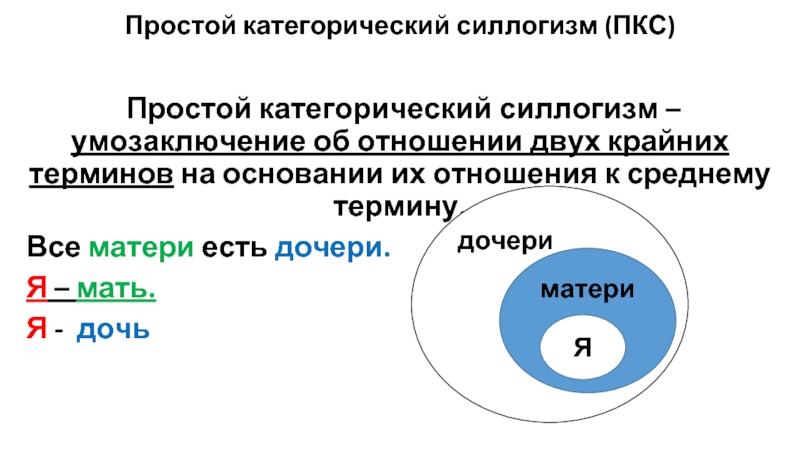
Слайд 15Простой категорический силлогизм (ПКС)
Простой категорический силлогизм – умозаключение об отношении
двух крайних терминов на основании их отношения к среднему термину.
Все матери есть дочери.
Я – мать.
Я - дочь
Все матери есть дочери.
Я – мать.
Я - дочь
дочери
матери
Я
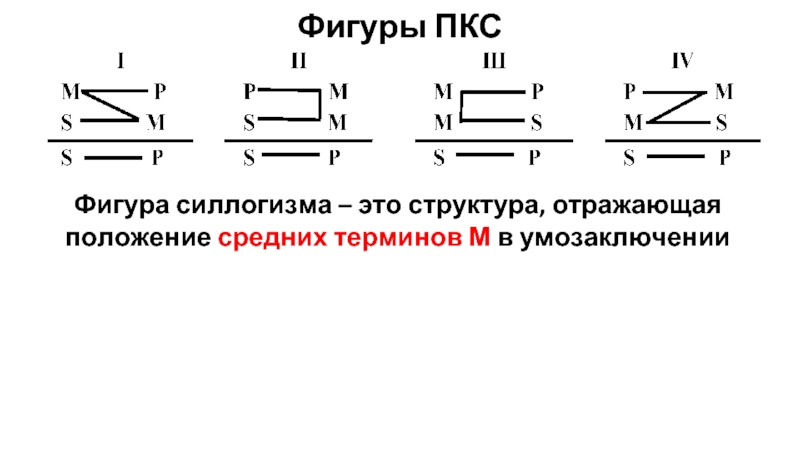
Слайд 16Фигуры ПКС
Фигура силлогизма – это структура, отражающая положение средних терминов
М в умозаключении
Слайд 18Правила ПКС
Для получения истинного заключения необходимо соблюдать:
три правила терминов ПКС
четыре правила
посылок ПКС
Слайд 19Правила терминов ПКС
1. В ПКС должно быть только три термина.
2.
Средний термин М должен быть распределен хотя бы в одной из посылок.
3. Термин, нераспределенный в посылке, не может быть распределен и в заключении.
Распределенность терминов в посылках:
3. Термин, нераспределенный в посылке, не может быть распределен и в заключении.
Распределенность терминов в посылках:
Слайд 20Правила посылок ПКС
1. Хотя бы одна из посылок должна быть утвердительным
суждением. Их двух отрицательных посылок нельзя сделать никакого заключения.
2 Хотя бы одна из посылок должна быть общим суждением. Из двух частных суждений заключение с необходимостью не следует
3. Если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным.
4. Если одна из посылок – частное суждение, то и заключение должно быть частным
2 Хотя бы одна из посылок должна быть общим суждением. Из двух частных суждений заключение с необходимостью не следует
3. Если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным.
4. Если одна из посылок – частное суждение, то и заключение должно быть частным
Слайд 21Сильные модусы ПКС
Сильные = необходимые, правильные модусы ПКС.
Так как есть правила
терминов и посылок ПКС, то не все модусы ПКС являются правильными и сильными!!
Всего – 64 модуса, какие из них сильные?
Всего – 64 модуса, какие из них сильные?




![Способы превращения:Двойное отрицание: утвердительные суждения → в отрицательные: [S есть P] → [S не есть](/img/tmb/3/218738/cff40d5854635a3a6e55d86f3d538cff-800x.jpg)


![A →E: [Все S есть P] →](/img/tmb/3/218738/02104c19f12cb9b601b9bc6e191663bd-800x.jpg)




![Простой категорический силлогизм (ПКС)Структура ПКС:Все металлы [S] электропроводны [P].](/img/tmb/3/218738/9de5e1b736d219fc9c8a61805b24c018-800x.jpg)