Понятие "черного ящика" презентация

Содержание

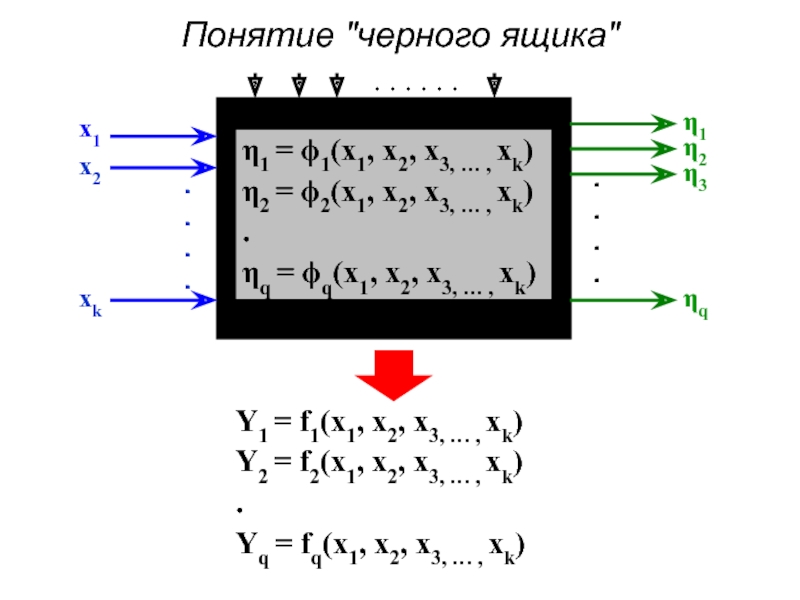
2. Понятие "черного ящика"
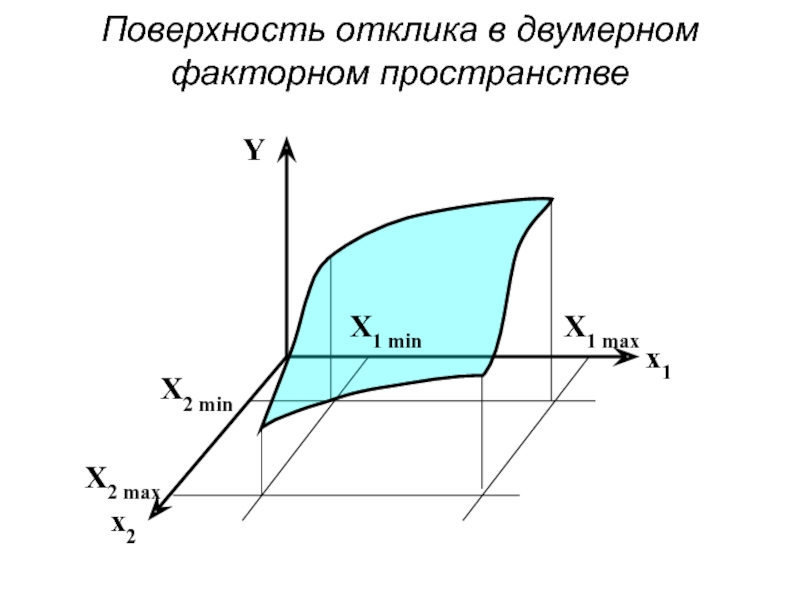
3. Поверхность отклика в двумерном факторном пространстве
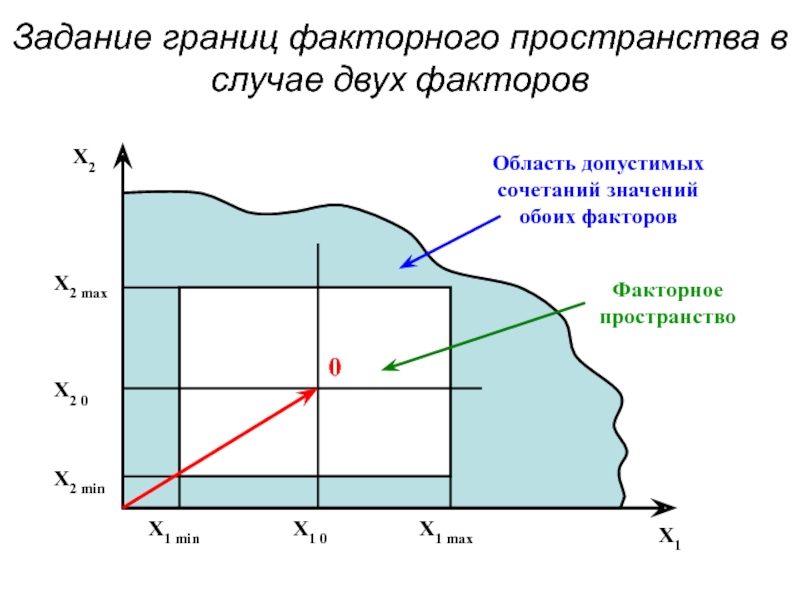
4. Задание границ факторного пространства в случае двух факторов
5. Разложение неизвестной функции в ряд Тейлора
6. Пересчет реальных значений факторов в масштабные
7. Матрица полного факторного эксперимента
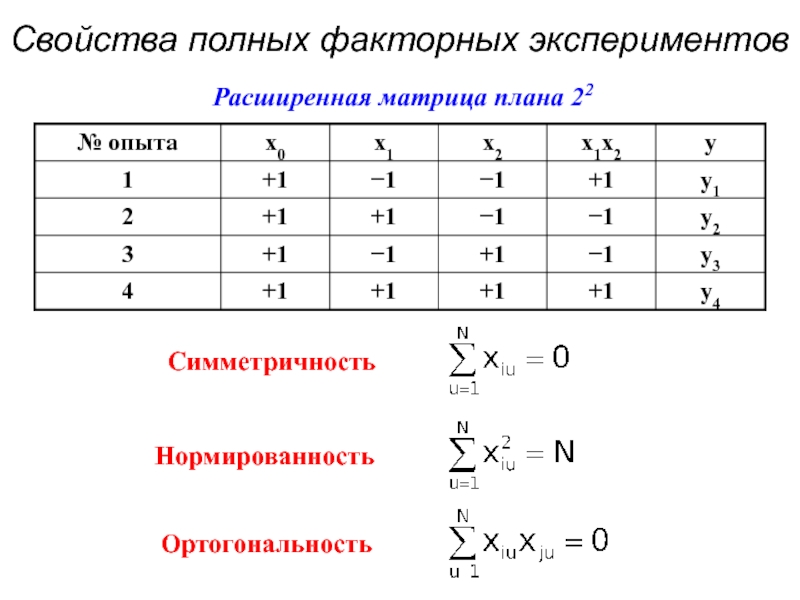
8. Свойства полных факторных экспериментов Расширенная матрица плана 22
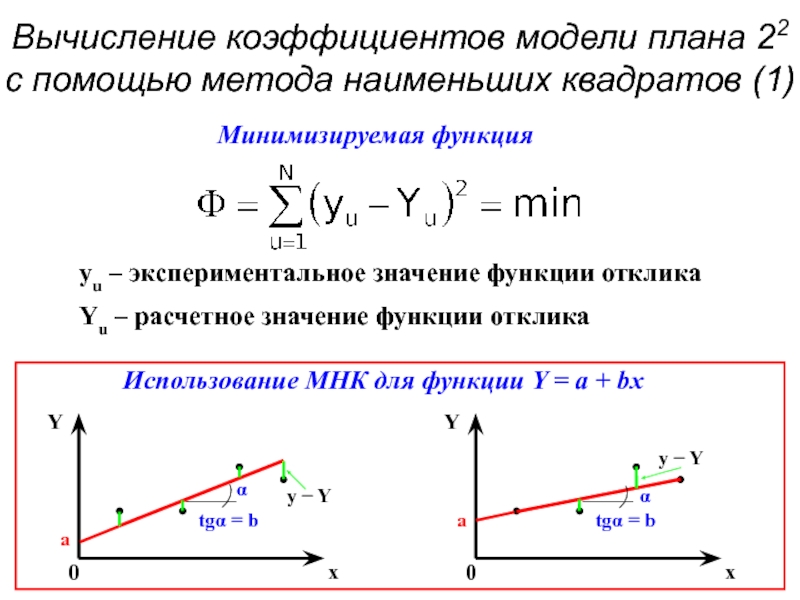
9. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (1)
10. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (2)
11. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (3)
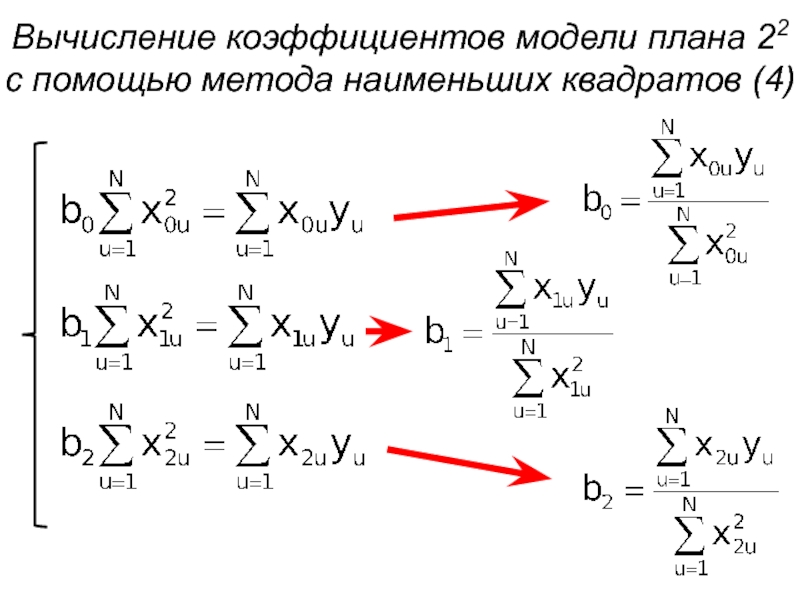
12. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (4)
13. Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (5)
14. Расчет среднего значения и дисперсии функции отклика
15. Расчет средних значений и дисперсии опытов при неравномерном дублировании
16. Расчет средних значений и дисперсии опытов при равномерном дублировании
17. Проверка ряда дисперсий на однородность по критерию Кохрена при равномерном дублировании
18. Проверка статистической значимости коэффициентов уравнения регрессии
19. Проверка значимости уравнения регрессии (1)
20. Проверка значимости уравнения регрессии (2)
21. Проверка значимости уравнения регрессии (3)
22. Преобразование уравнения регрессии под реальное представление факторов
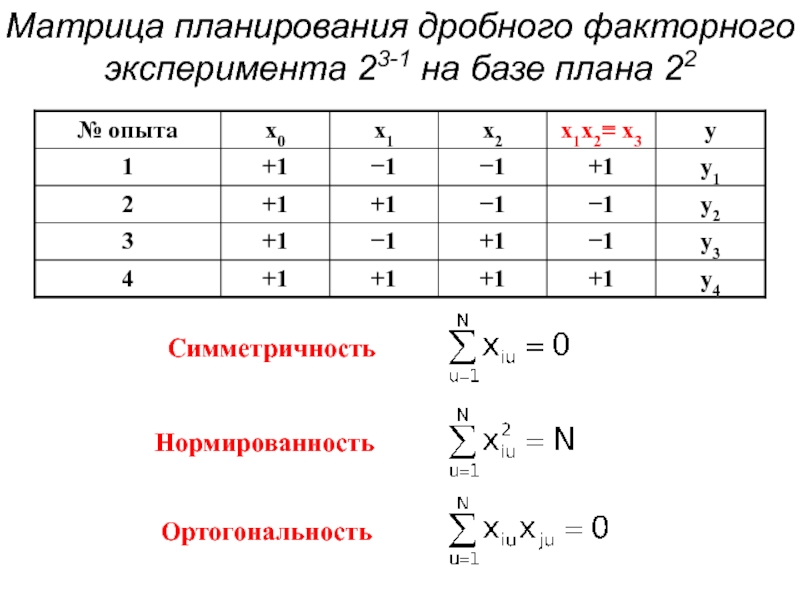
23. Матрица планирования дробного факторного эксперимента 23-1 на базе плана 22
24. Смешивание эффектов в дробных факторных экспериментах
25. Понятия генерирующего соотношения и определяющего контраста
26. Матрица ДФЭ 24-1с определяющим контрастом 1 ≡ x1x2x3x4
27. Матрица ДФЭ 24-1с определяющим контрастом 1 ≡ x1x2x4
28. Планы второго порядка
29. Матрица композиционного плана на базе плана 22
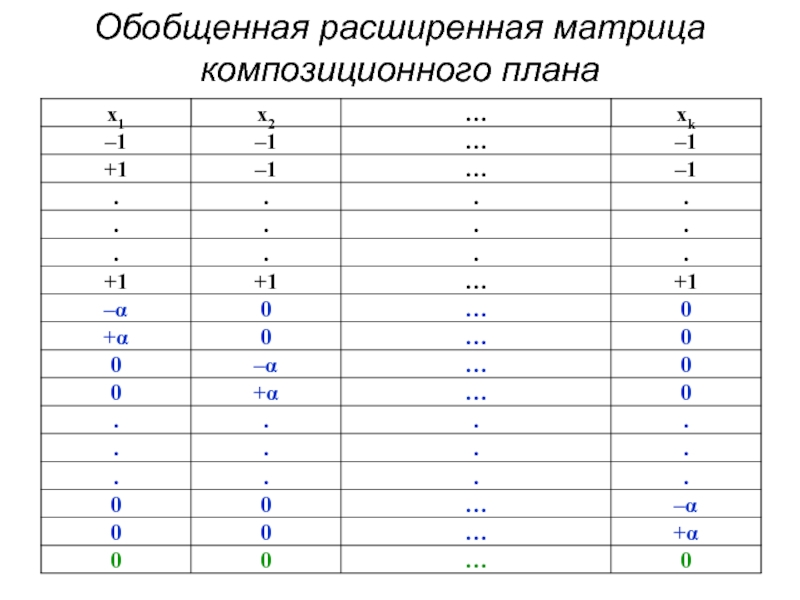
30. Обобщенная расширенная матрица композиционного плана
31. Нечетные моменты плана
32. Четные моменты плана
33. Вспомогательные коэффициенты для расчета коэффициентов уравнений регрессии
34. Расчет коэффициентов уравнения регрессии композиционных планов (1)
35. Расчет коэффициентов уравнения регрессии композиционных планов (2)
36. Дисперсия оценки коэффициентов регрессии
37. Условие D-оптимальности для непрерывных симметричных планов
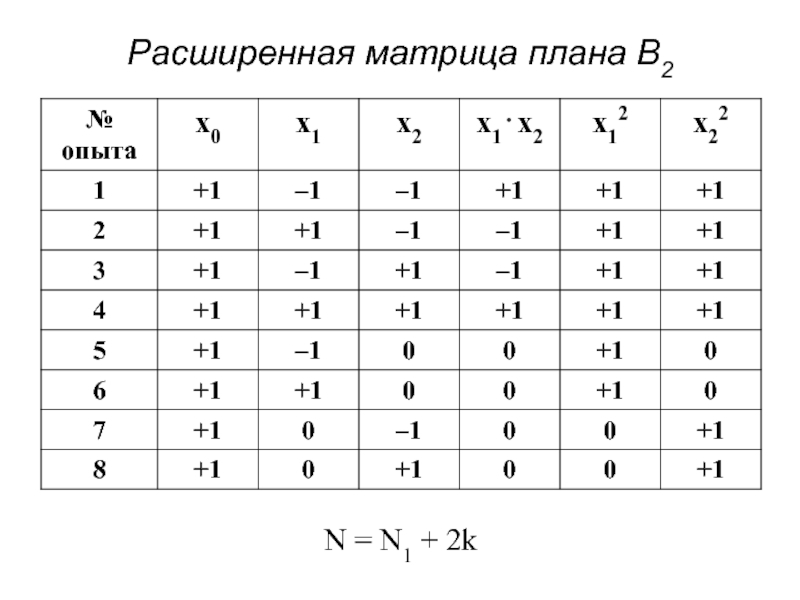
38. Расширенная матрица плана B2 N = N1 + 2k
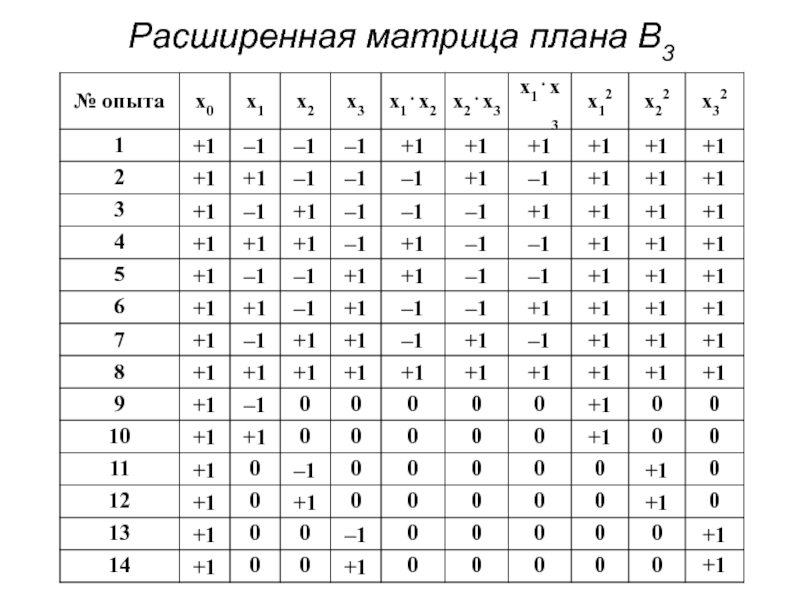
39. Расширенная матрица плана B3
40. Расчет коэффициентов уравнения регрессии композиционного плана Bk
41. Расчет дисперсий и среднеквадратических ошибок оценок коэффициентов
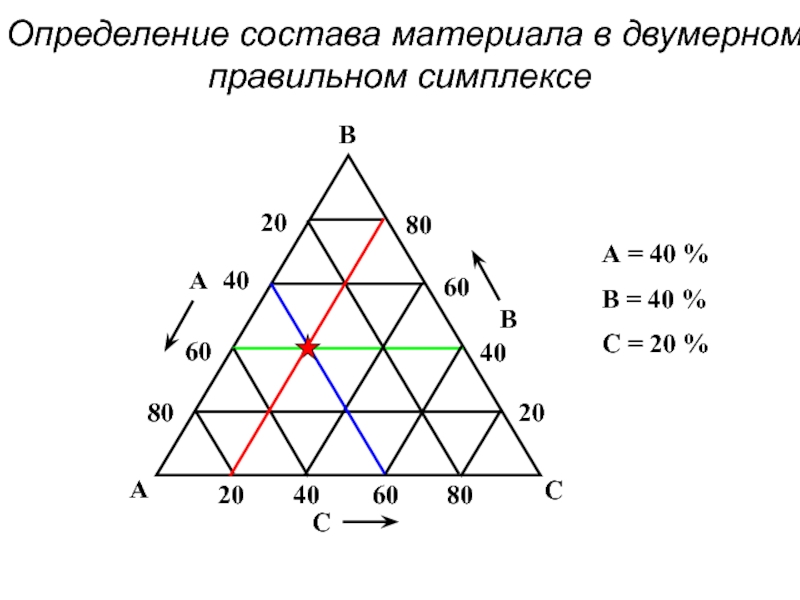
42. Определение состава материала в двумерном правильном симплексе
43. Преобразование полиномиального регрессионного уравнения в каноническую форму Шеффе (1)
44. Преобразование полиномиального регрессионного уравнения в каноническую форму
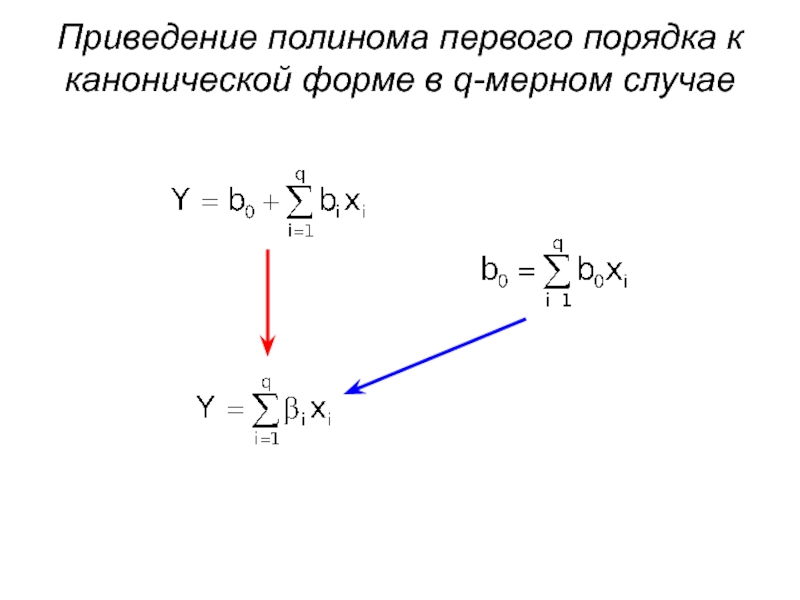
45. Приведение полинома первого порядка к канонической форме в q-мерном случае
46. Приведение полинома второго порядка к канонической форме в q-мерном случае
47. Приведение полинома третьего порядка к канонической форме
48. Симплекс-решетчатые планы
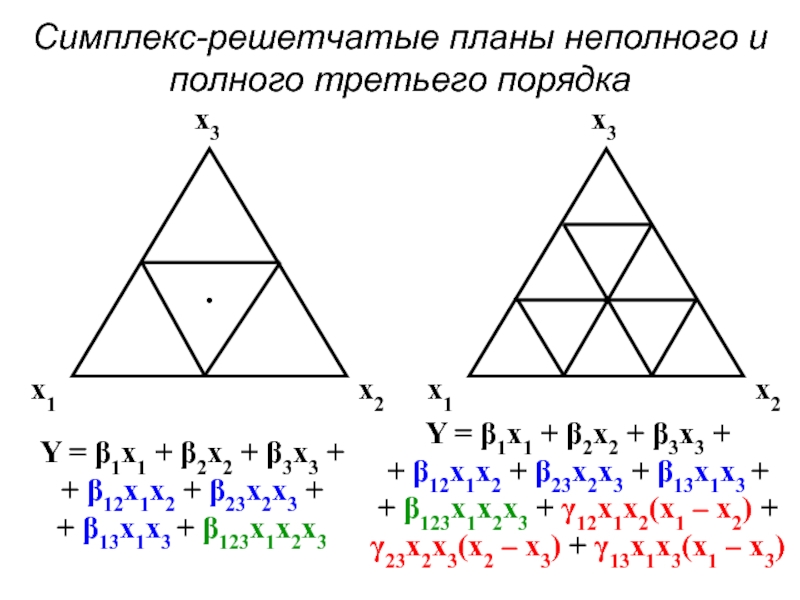
49. Симплекс-решетчатые планы неполного и полного третьего порядка
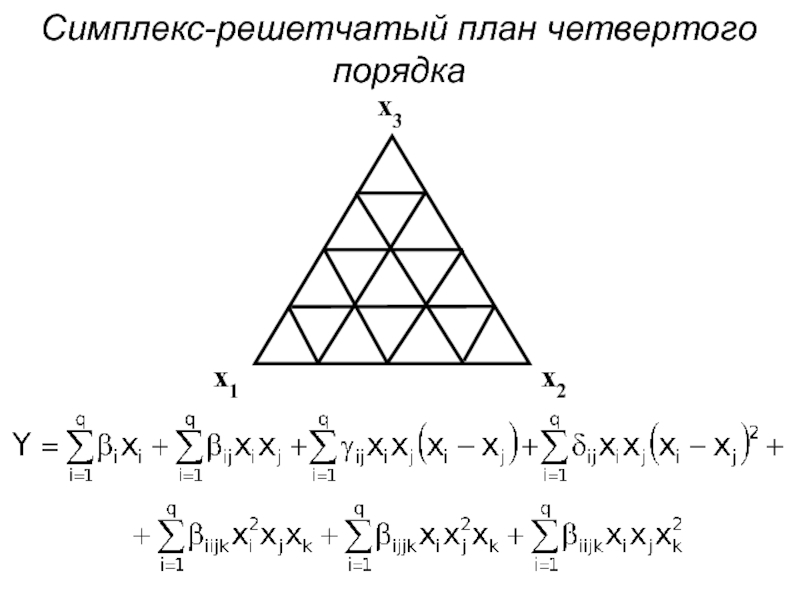
50. Симплекс-решетчатый план четвертого порядка
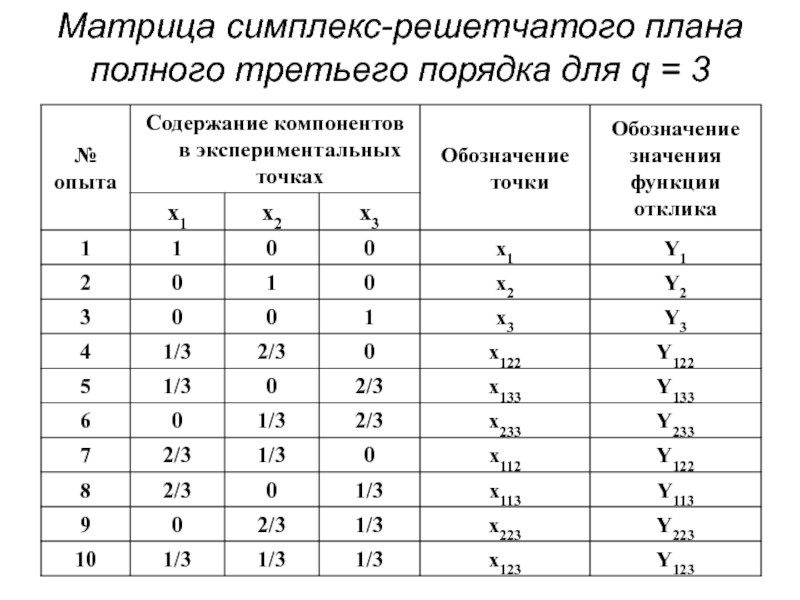
51. Матрица симплекс-решетчатого плана полного третьего порядка для q = 3
52. Расчет коэффициентов уравнения регрессии методом подстановки (1)
53. Расчет коэффициентов уравнения регрессии методом подстановки (2)
54. Расчет коэффициентов уравнения регрессии для плана неполного
55. Расчет коэффициентов уравнения регрессии для плана полного
56. Проверка адекватности уравнения регрессии по критерию Сьюдента (1)
57. Проверка адекватности уравнения регрессии по критерию Сьюдента (2)
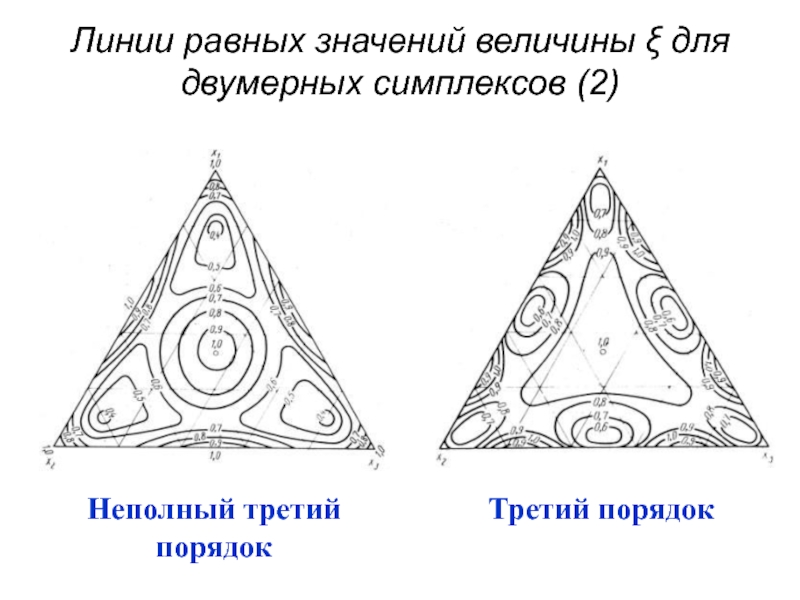
58. Линии равных значений величины ξ для двумерных симплексов (1)
59. Линии равных значений величины ξ для двумерных симплексов (2)
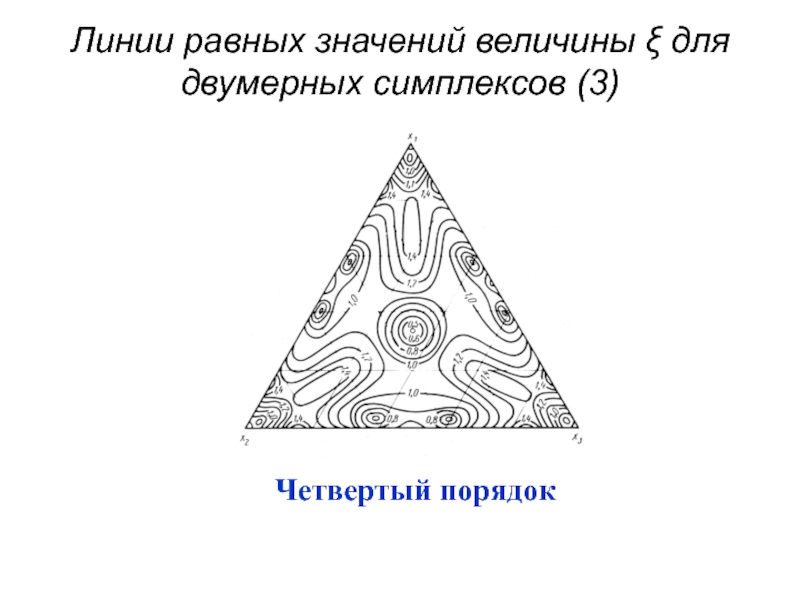
60. Линии равных значений величины ξ для двумерных симплексов (3)
61. Расчет значений ξ (1)
62. Расчет значений ξ (2)
63. Оценка дисперсии значений, предсказанных моделью (1)
64. Оценка дисперсии значений, предсказанных моделью (2)
65. Оценка дисперсии значений, предсказанных моделью (3)
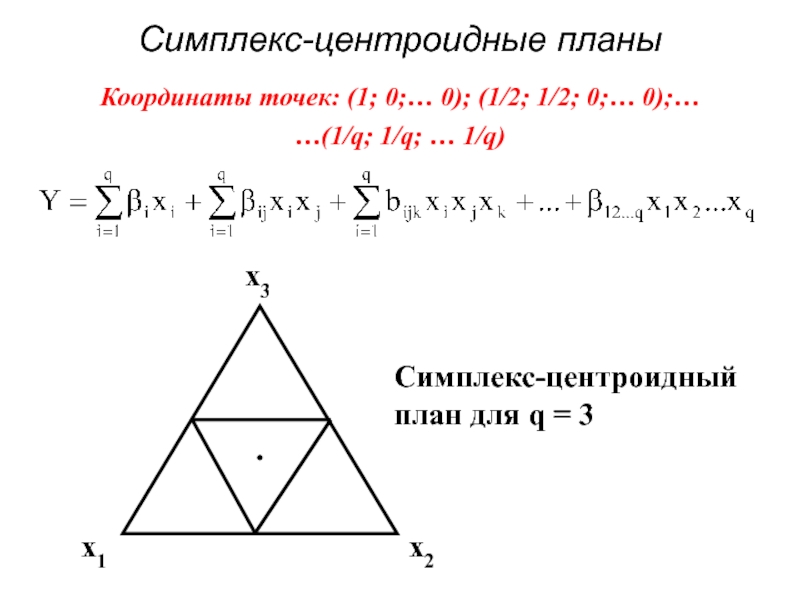
66. Симплекс-центроидные планы Координаты точек: (1; 0;… 0);
67. D-оптимальные планы Координаты точек модели третьего порядка
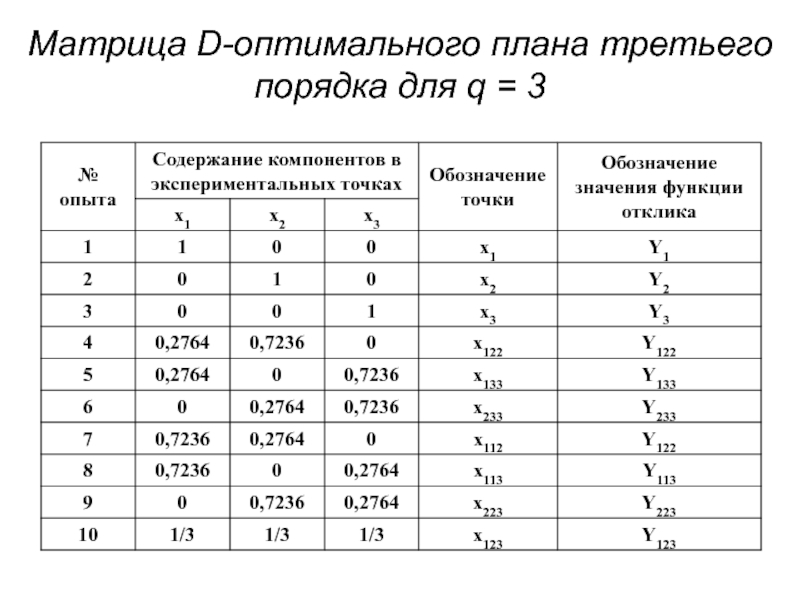
68. Матрица D-оптимального плана третьего порядка для q = 3
69. Расчет коэффициентов уравнения регрессии для D-оптимального плана
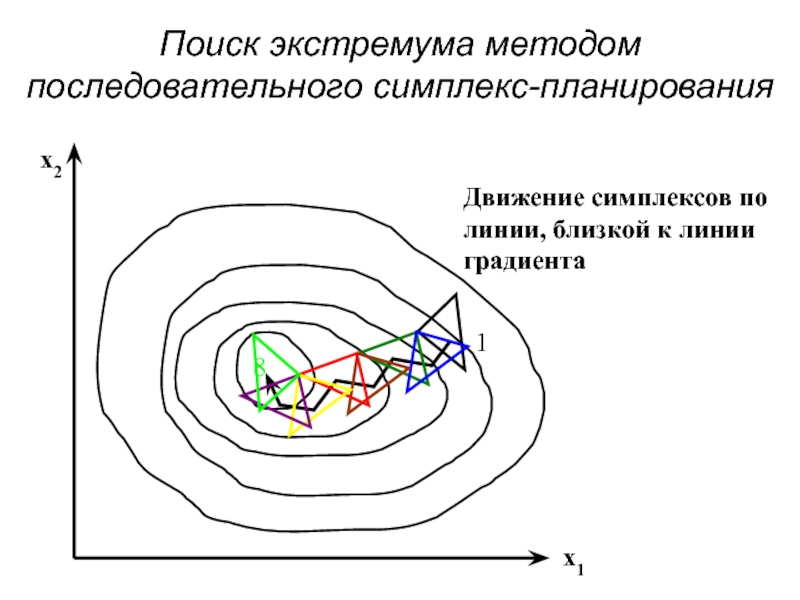
70. Поиск экстремума методом последовательного симплекс-планирования
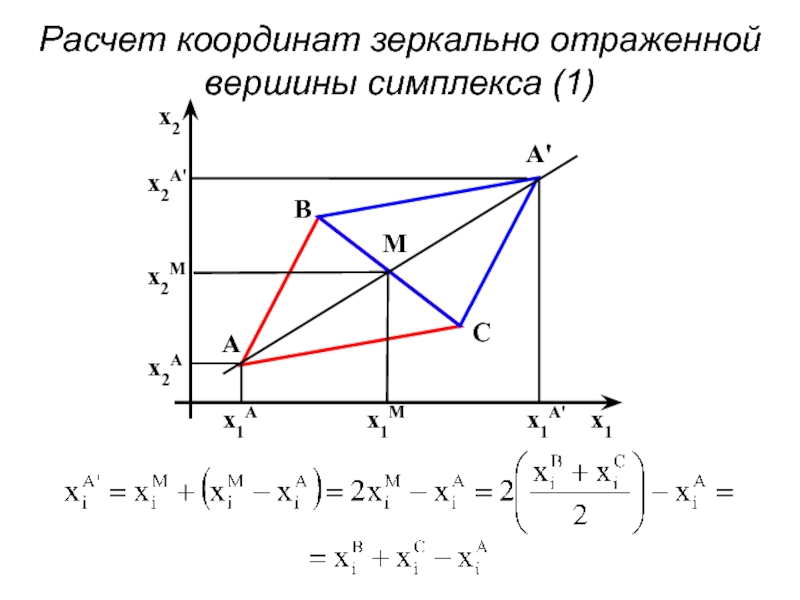
71. Расчет координат зеркально отраженной вершины симплекса (1)
72. Расчет координат зеркально отраженной вершины симплекса (2)
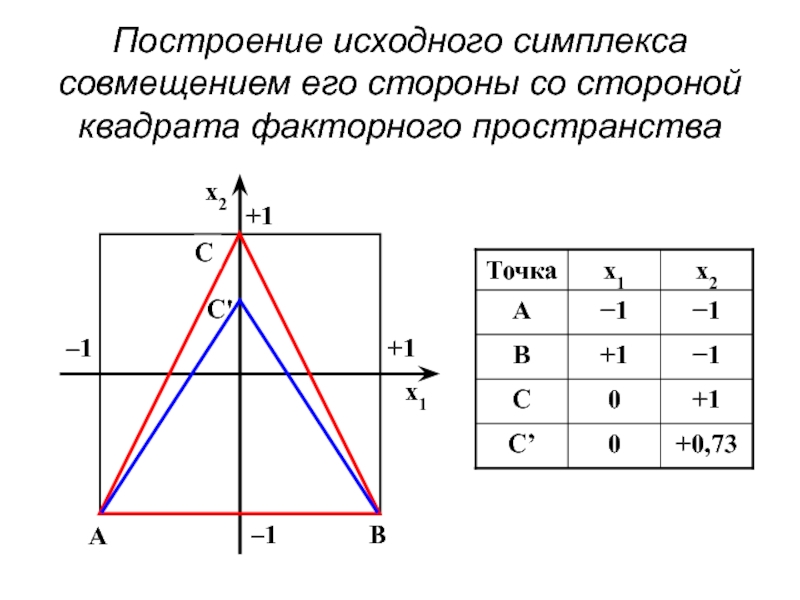
73. Построение исходного симплекса совмещением его стороны со стороной квадрата факторного пространства
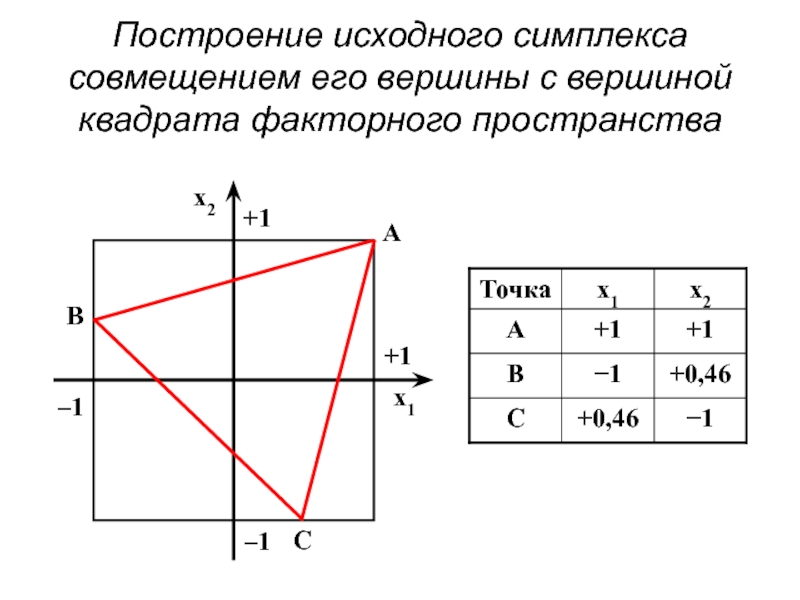
74. Построение исходного симплекса совмещением его вершины с вершиной квадрата факторного пространства
75. Построение исходного симплекса совмещением его центра тяжести
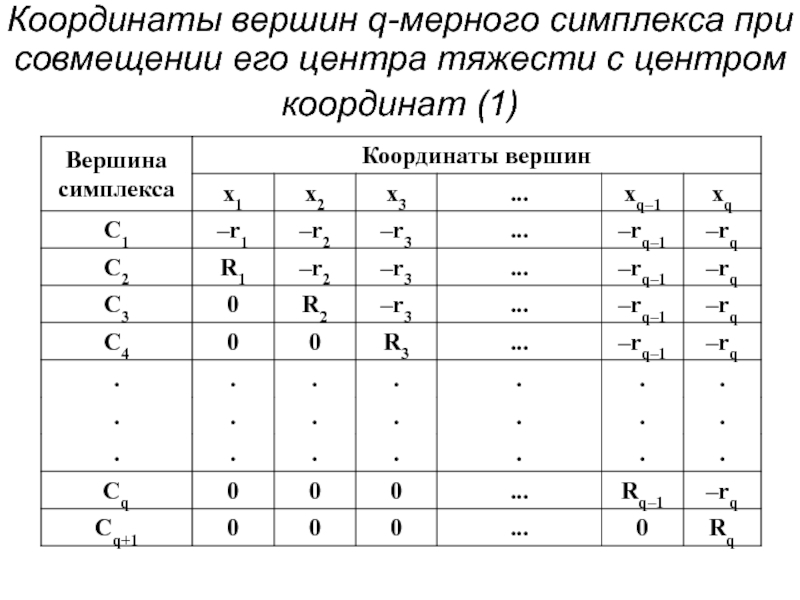
76. Координаты вершин q-мерного симплекса при совмещении его центра тяжести с центром координат (1)
77. Координаты вершин q-мерного симплекса при совмещении его
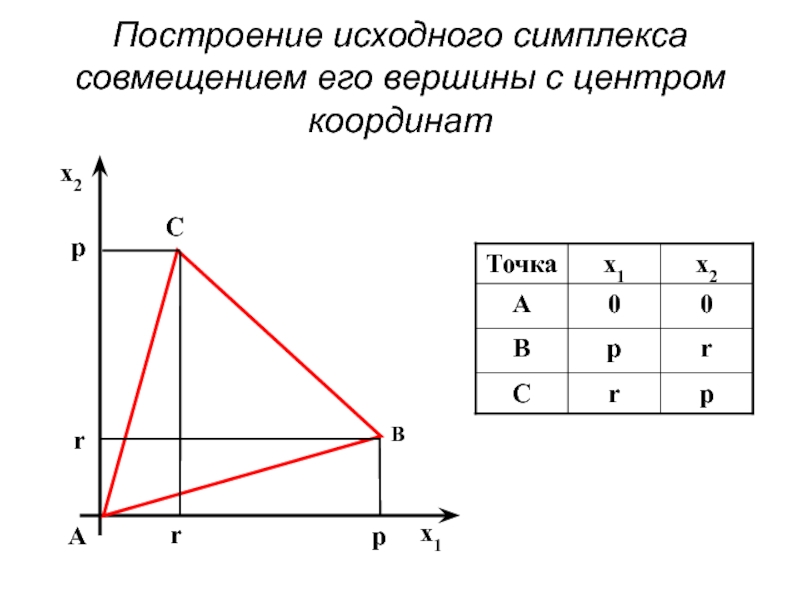
78. Построение исходного симплекса совмещением его вершины с центром координат
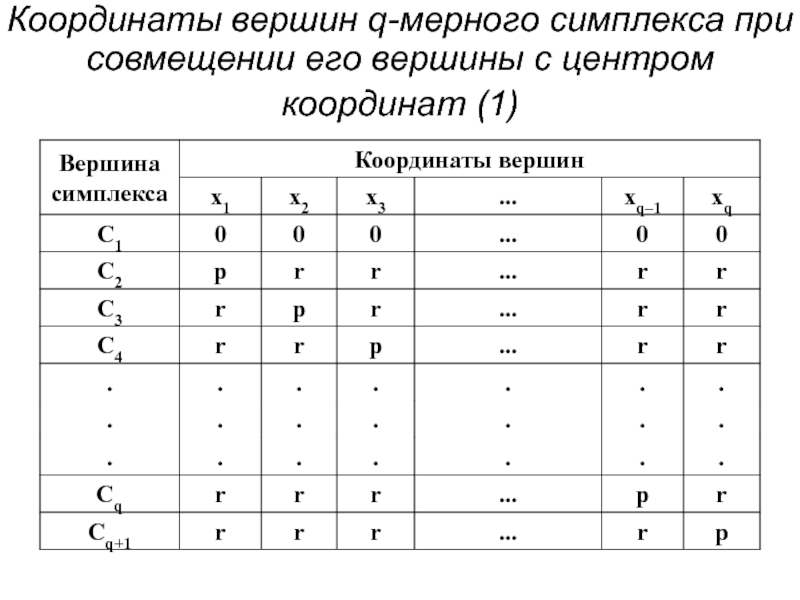
79. Координаты вершин q-мерного симплекса при совмещении его вершины с центром координат (1)
80. Координаты вершин q-мерного симплекса при совмещении его
81. Качание симплекса относительно одной грани С7 С9 С8 С10
82. Метод деформированного симплекса где:
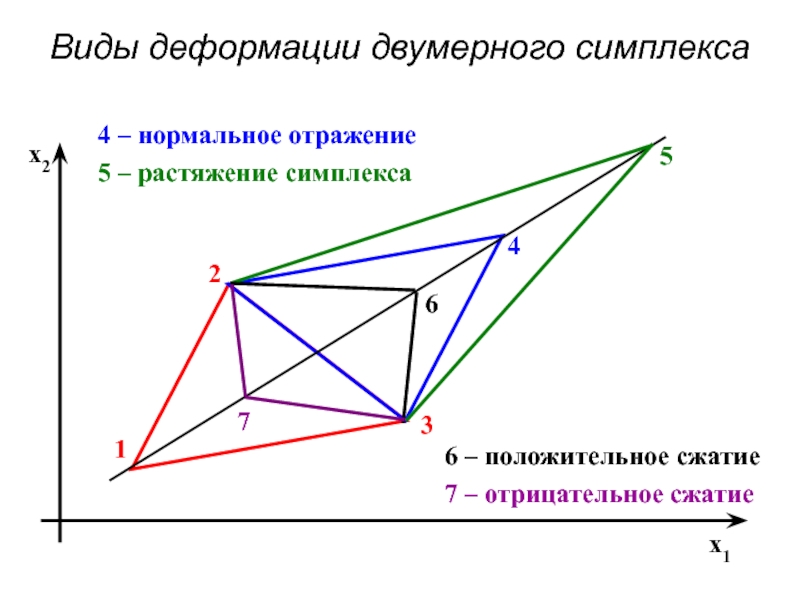
83. Виды деформации двумерного симплекса
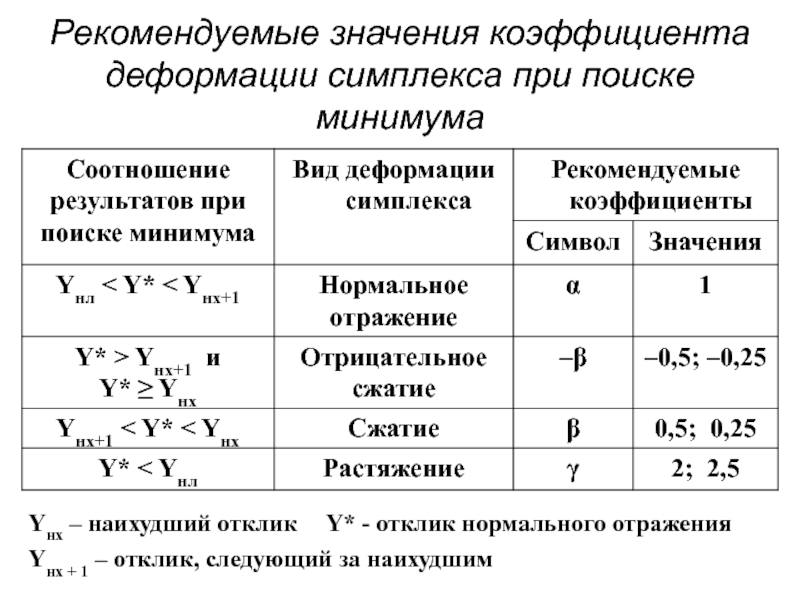
84. Рекомендуемые значения коэффициента деформации симплекса при поиске
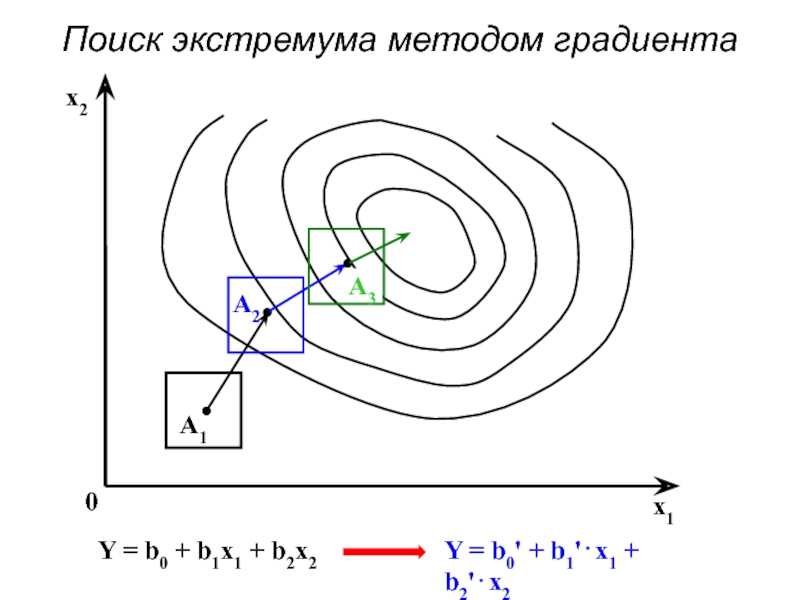
85. Поиск экстремума методом градиента
86. Использование компонентов градиента при переходе на следующий уровень функции отклика
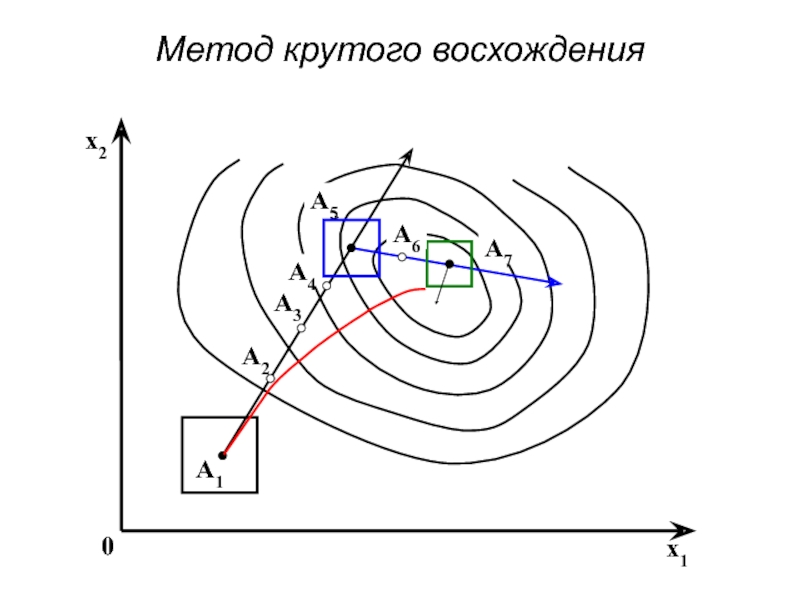
87. Метод крутого восхождения
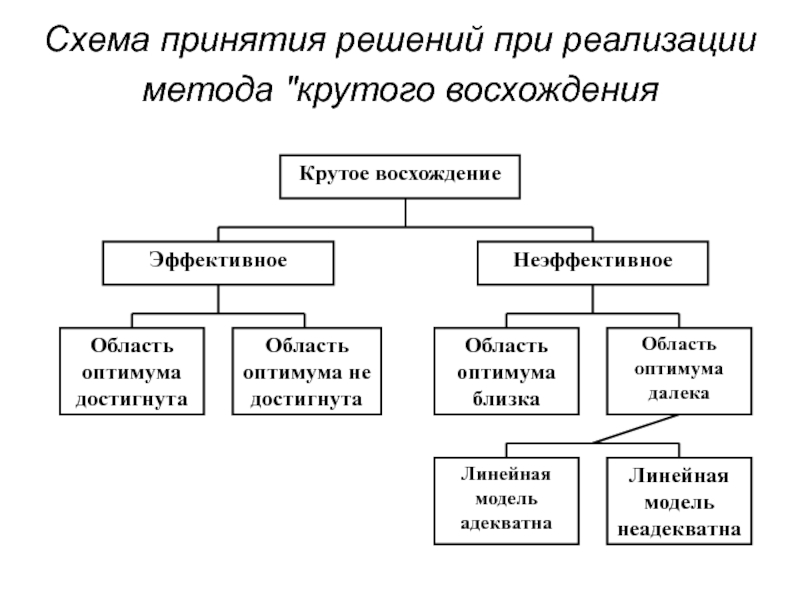
88. Схема принятия решений при реализации метода "крутого восхождения
89. Обобщенный параметр оптимизации
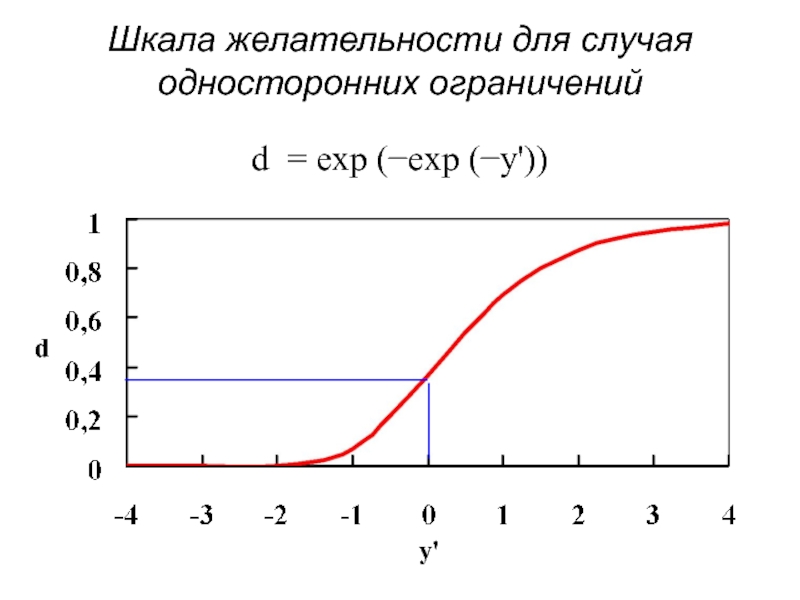
90. Шкала желательности для случая односторонних ограничений d = exp (−exp (−y')) y' d
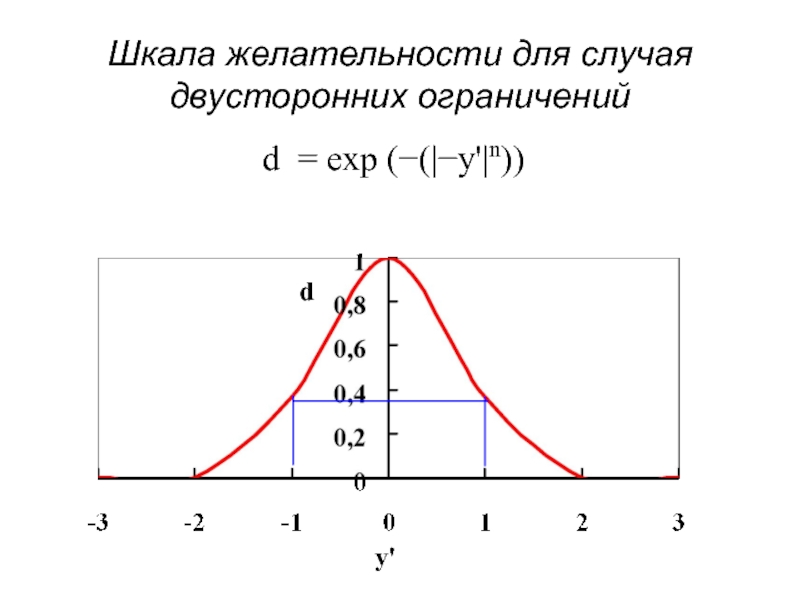
91. Шкала желательности для случая двусторонних ограничений d = exp (−(|−y'|n)) y' d

Понятие "черного ящика"

Слайд 1

Слайд 2Понятие "черного ящика"

Слайд 3Поверхность отклика в двумерном факторном пространстве

Слайд 4Задание границ факторного пространства в случае двух факторов

Слайд 5Разложение неизвестной функции в ряд Тейлора

Слайд 6Пересчет реальных значений факторов в масштабные

Слайд 7Матрица полного факторного эксперимента

Слайд 8Свойства полных факторных экспериментов
Расширенная матрица плана 22

Слайд 9Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (1)

Слайд 10Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (2)

Слайд 11Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (3)

Слайд 12Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (4)

Слайд 13Вычисление коэффициентов модели плана 22 с помощью метода наименьших квадратов (5)

Слайд 14Расчет среднего значения и дисперсии функции отклика при дублировании опытов в

центре плана

Слайд 15Расчет средних значений и дисперсии опытов при неравномерном дублировании

Слайд 16Расчет средних значений и дисперсии опытов при равномерном дублировании

Слайд 17Проверка ряда дисперсий на однородность по критерию Кохрена при равномерном дублировании

Слайд 18Проверка статистической значимости коэффициентов уравнения регрессии

Слайд 19Проверка значимости уравнения регрессии (1)

Слайд 20Проверка значимости уравнения регрессии (2)

Слайд 21Проверка значимости уравнения регрессии (3)

Слайд 22Преобразование уравнения регрессии под реальное представление факторов

Слайд 23Матрица планирования дробного факторного эксперимента 23-1 на базе плана 22

Слайд 24Смешивание эффектов в дробных факторных экспериментах

Слайд 25Понятия генерирующего соотношения и определяющего контраста

Слайд 26Матрица ДФЭ 24-1с определяющим контрастом 1 ≡ x1x2x3x4

Слайд 27Матрица ДФЭ 24-1с определяющим контрастом 1 ≡ x1x2x4

Слайд 28Планы второго порядка

Слайд 29Матрица композиционного плана на базе плана 22
Общее число опытов в композиционных

планах с k факторами

Слайд 30Обобщенная расширенная матрица композиционного плана

Слайд 31Нечетные моменты плана

Слайд 32Четные моменты плана

Слайд 33Вспомогательные коэффициенты для расчета коэффициентов уравнений регрессии композиционных планов

Проверка правильности расчетов

вспомогательных коэффициентов

Слайд 34Расчет коэффициентов уравнения регрессии композиционных планов (1)

Слайд 35Расчет коэффициентов уравнения регрессии композиционных планов (2)

Слайд 36Дисперсия оценки коэффициентов регрессии

Слайд 37Условие D-оптимальности для непрерывных симметричных планов

Слайд 38Расширенная матрица плана B2
N = N1 + 2k

Слайд 39Расширенная матрица плана B3

Слайд 40Расчет коэффициентов уравнения регрессии композиционного плана Bk

Слайд 41Расчет дисперсий и среднеквадратических ошибок оценок коэффициентов

Слайд 42Определение состава материала в двумерном правильном симплексе

Слайд 43Преобразование полиномиального регрессионного уравнения в каноническую форму Шеффе (1)

Слайд 44Преобразование полиномиального регрессионного уравнения в каноническую форму Шеффе (2)

Каноническая форма Шеффе

Y

= (b0 + b1 + b11)x1 + (b0 + b2 + b22)x2 + (b0 + b3 + b33)x3 + (b12 – b11 – b22)x1x2 + (b13 – b11 – b33)x1x3 +
+ (b23 – b22 – b33)x2x3

βi = b0 + bi + bii
βij = bij – bii – bij

Y = β1x1 + β2x2 + β3x3 + β12x1x2 + β13x1x3 + β23x2x3

Слайд 45Приведение полинома первого порядка к канонической форме в q-мерном случае

Слайд 46Приведение полинома второго порядка к канонической форме в q-мерном случае

Слайд 47Приведение полинома третьего порядка к канонической форме в q-мерном случае

Слайд 48Симплекс-решетчатые планы

Слайд 49Симплекс-решетчатые планы неполного и полного третьего порядка

Слайд 50Симплекс-решетчатый план четвертого порядка

Слайд 51Матрица симплекс-решетчатого плана полного третьего порядка для q = 3

Слайд 52Расчет коэффициентов уравнения регрессии методом подстановки (1)

Слайд 53Расчет коэффициентов уравнения регрессии методом подстановки (2)

Слайд 54Расчет коэффициентов уравнения регрессии для плана неполного третьего порядка
βi =Yi
βij =

4Yij – 2Yi – 2Yj
β123 = 27Y123 – 12(Y12 + Y23 + Y13) + + 3(Y1 + Y2 + Y3)

Слайд 55Расчет коэффициентов уравнения регрессии для плана полного третьего порядка
βi =Yi
βij =

9/4 (Yiij + Yijj– Yi – Yj)
β123 = 27Y123 – 27/4 (Y112 + Y122 + Y223 + + Y233 + Y113 + Y133) + 9/2 (Y1 + Y2 + Y3)
γij = 9/4 (3Yiij – 3Yijj– Yi + Yj)

Слайд 56Проверка адекватности уравнения регрессии по критерию Сьюдента (1)

Слайд 57Проверка адекватности уравнения регрессии по критерию Сьюдента (2)

Слайд 58Линии равных значений величины ξ для двумерных симплексов (1)

Слайд 59Линии равных значений величины ξ для двумерных симплексов (2)

Слайд 60Линии равных значений величины ξ для двумерных симплексов (3)

Слайд 61Расчет значений ξ (1)

Слайд 62Расчет значений ξ (2)

Слайд 63Оценка дисперсии значений, предсказанных моделью (1)

Слайд 64Оценка дисперсии значений, предсказанных моделью (2)

Слайд 65Оценка дисперсии значений, предсказанных моделью (3)

Слайд 66Симплекс-центроидные планы
Координаты точек: (1; 0;… 0); (1/2; 1/2; 0;… 0);…
…(1/q;

1/q; … 1/q)

Симплекс-центроидный план для q = 3

Слайд 67D-оптимальные планы
Координаты точек модели третьего порядка для q факторов: (1; 0;…

0); (0,7236; 0,2764; 0;… 0); (1/3; 1/3; 1/3; 0;… 0)

Координаты точек модели четвертого порядка для q факторов: (1; 0;… 0); (1/2; 1/2; 0;… 0); (0,8273; 0,1727; 0;… 0); (0,5670; 0,2165; 0,2165; 0;… 0); (1/4; 1/4; 1/4; 1/4; 0;… 0)

Слайд 68Матрица D-оптимального плана третьего порядка для q = 3

Слайд 69Расчет коэффициентов уравнения регрессии для D-оптимального плана третьего порядка
βi =Yi
βij =

2,5 (Yiij + Yijj– Yi – Yj)
β123 = 27Y123 – 7,5 (Y112 + Y122 + Y223 + + Y233 + Y113 + Y133) + 6 (Y1 + Y2 + Y3)
γij = 2,5 (Yi – Yj) + 2,5·50,5 (Yiij – Yijj)

Слайд 70Поиск экстремума методом последовательного симплекс-планирования

Слайд 71Расчет координат зеркально отраженной вершины симплекса (1)

Слайд 72Расчет координат зеркально отраженной вершины симплекса (2)

i – номер фактора
q –число

факторов
* – индекс новой (зеркальной) вершины
f – индекс вершины с наихудшим значением отклика
1; 2; (f – 1); (f + 1) – индексы остальных вершин симплекса

Слайд 73Построение исходного симплекса совмещением его стороны со стороной квадрата факторного пространства

Слайд 74Построение исходного симплекса совмещением его вершины с вершиной квадрата факторного пространства

Слайд 75Построение исходного симплекса совмещением его центра тяжести с центром координат
R1 =

r1 = 0,5

Слайд 76Координаты вершин q-мерного симплекса при совмещении его центра тяжести с центром

координат (1)

Слайд 77Координаты вершин q-мерного симплекса при совмещении его центра тяжести с центром

координат (2)

Слайд 78Построение исходного симплекса совмещением его вершины с центром координат

Слайд 79Координаты вершин q-мерного симплекса при совмещении его вершины с центром координат

(1)

Слайд 80Координаты вершин q-мерного симплекса при совмещении его вершины с центром координат

(2)

Слайд 81Качание симплекса относительно одной грани
С7
С9
С8
С10

Слайд 82Метод деформированного симплекса

где:

δ – коэффициент деформации симплекса
δ = α – нормальное

отражение
δ = β – сжатие симплекса
δ = γ – растяжение симплекса

Слайд 83Виды деформации двумерного симплекса

Слайд 84Рекомендуемые значения коэффициента деформации симплекса при поиске минимума
Yнх – наихудший отклик

Y* - отклик нормального отражения
Yнх + 1 – отклик, следующий за наихудшим

Слайд 85Поиск экстремума методом градиента

Слайд 86Использование компонентов градиента при переходе на следующий уровень функции отклика

Слайд 87Метод крутого восхождения

Слайд 88Схема принятия решений при реализации метода "крутого восхождения

Слайд 89Обобщенный параметр оптимизации

Слайд 90Шкала желательности для случая односторонних ограничений

d = exp (−exp (−y'))
y'
d

Слайд 91Шкала желательности для случая двусторонних ограничений
d = exp (−(|−y'|n))
y'
d

Скачать презентацию