- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Классическая логика высказываний. (Тема 3) презентация
Содержание
- 1. Классическая логика высказываний. (Тема 3)
- 2. Язык логики высказываний и семантика логических союзов
- 3. Определение формулы логики высказываний Пропозициональная переменная есть
- 4. A
- 5. Построение дерева формулы ((A → B) ∧
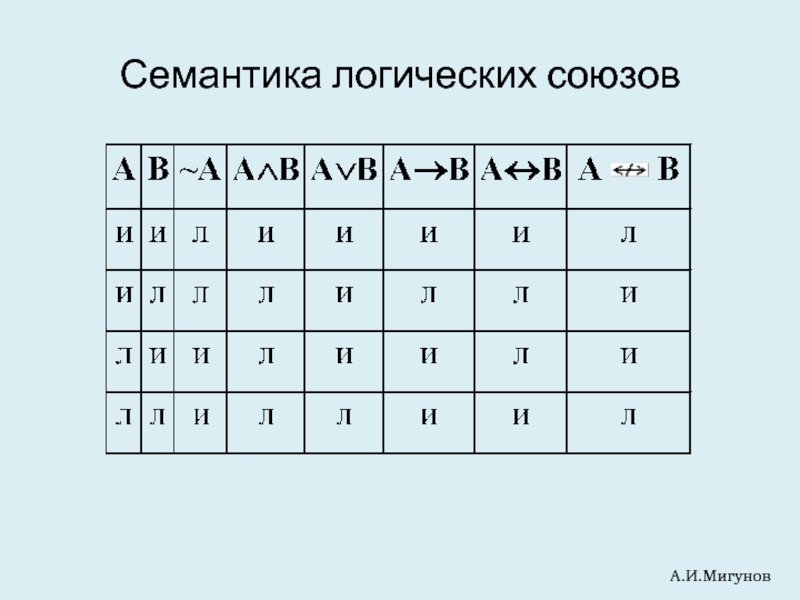
- 6. Семантика логических союзов А.И.Мигунов
- 7. p q
- 8. Или Сэм пойдет на вечеринку, и Макс
- 9. Таблицы истинности формул логики высказываний Некто А
- 10. Некто A говорит: «Если я рыцарь, то
- 11. «Это была первая наша встреча с Планом.
- 12. Если я рыцарь, то 2 х 2
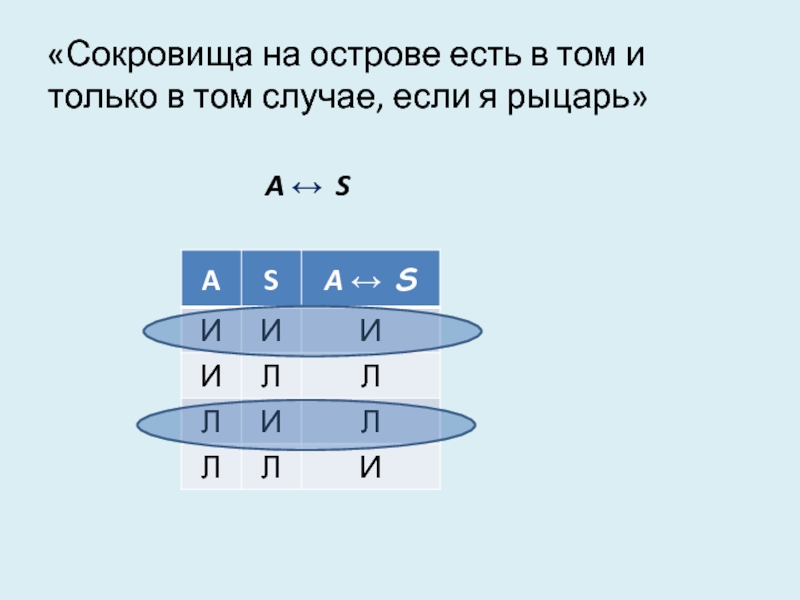
- 13. «Сокровища на острове есть в том и
- 14. Пример 1 Где сидит принцесса? Истинны ли
- 15. Где сидит принцесса?
- 16. Если магнит нагревать, то он размагнитится. Этот
- 17. Только «и» Хотя бы одно значение
- 18. Отношение логического следования Формула В логически следует
- 19. Отношение логического следования (Теорема дедукции) Задача установления
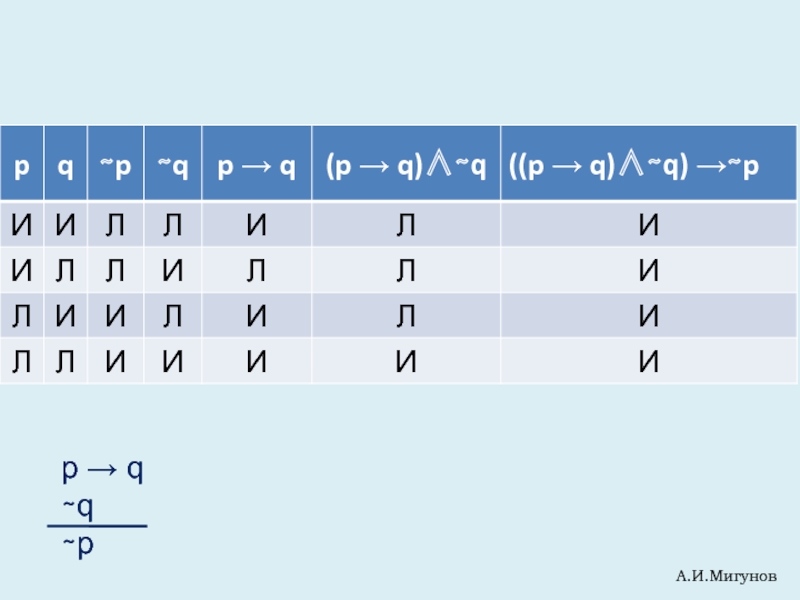
- 20. p → q ∼q
- 21. А.И.Мигунов p → q ∼q ∼p
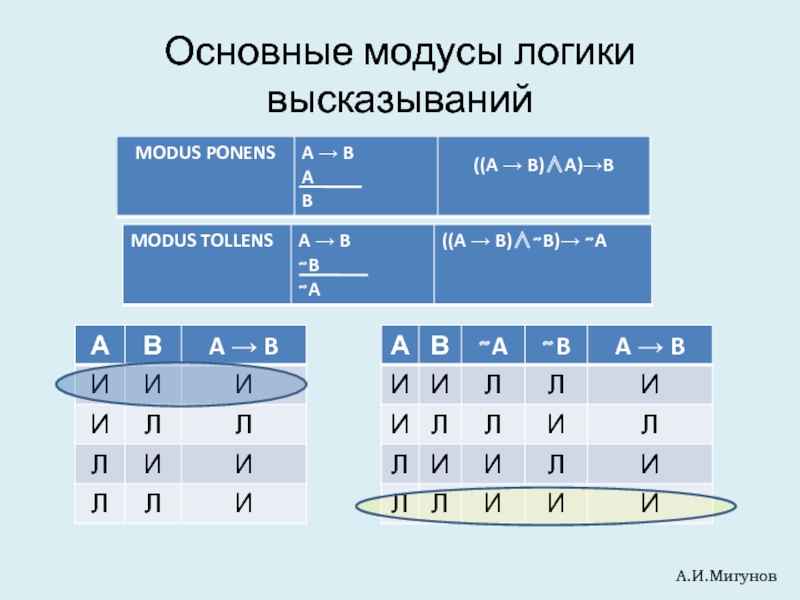
- 22. Основные модусы логики высказываний А.И.Мигунов
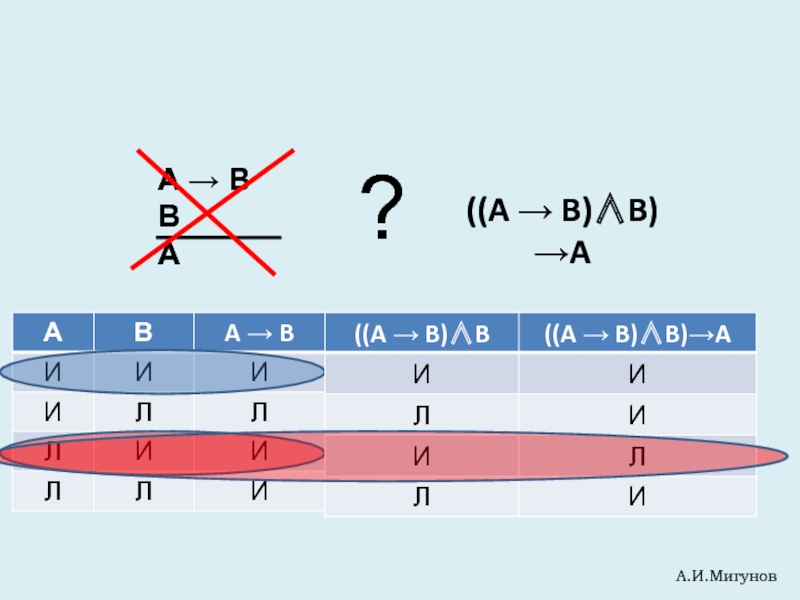
- 23. A → B В А ? А.И.Мигунов ((A → B)∧B)→A
- 24. Я заплатил бы за работу по ремонту
- 26. Необходимые и достаточные условия Я плачу за
- 27. Необходимые и достаточные условия P → R
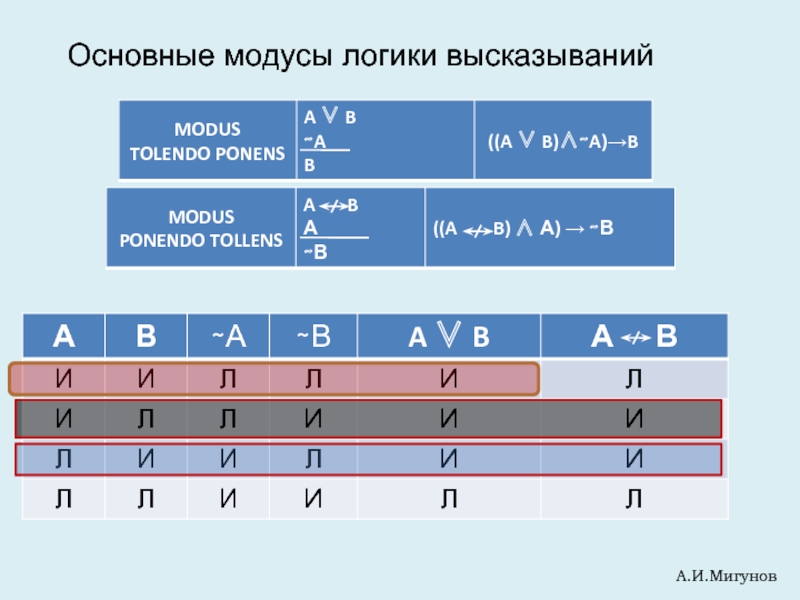
- 28. А.И.Мигунов Основные модусы логики высказываний
- 29. Основные модусы логики высказываний
- 30. Основные модусы логики высказываний
- 31. «Если ваши книги согласуются с Кораном, то
- 32. Зенон: Если тело находится в движении, то
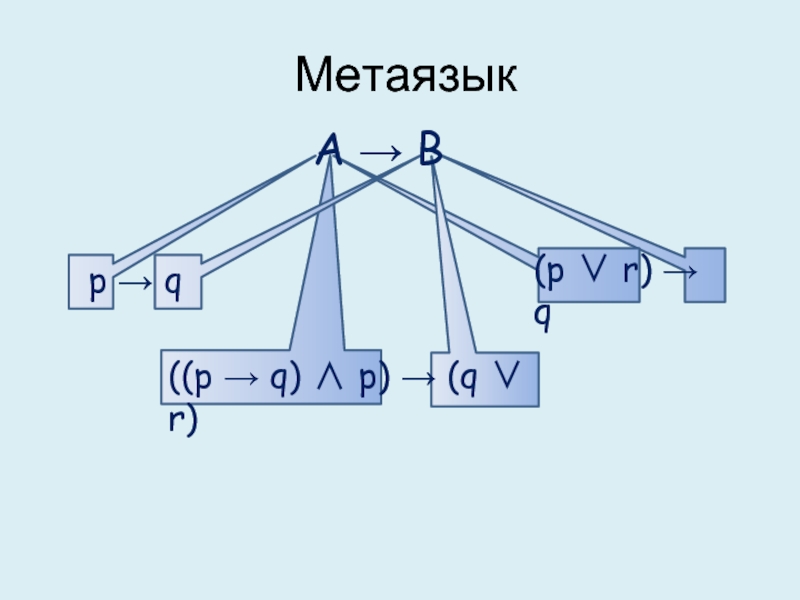
Слайд 2Язык логики высказываний и семантика логических союзов
Пропозициональные переменные
p, q, r, s,
Логические союзы (пропозициональные связки)
Технические знаки – (, ).
А.И.Мигунов
Слайд 3Определение формулы логики высказываний
Пропозициональная переменная есть формула;
если А – формула, то
если А – формула и В – формула, то
(А ∧ В), (А ∨ В), (А В), (А → В), (А ↔ В) – тоже формулы;
любая последовательность знаков из алфавита языка логики высказываний есть формула только в силу пунктов 1, 2, 3 данного определения.
А.И.Мигунов
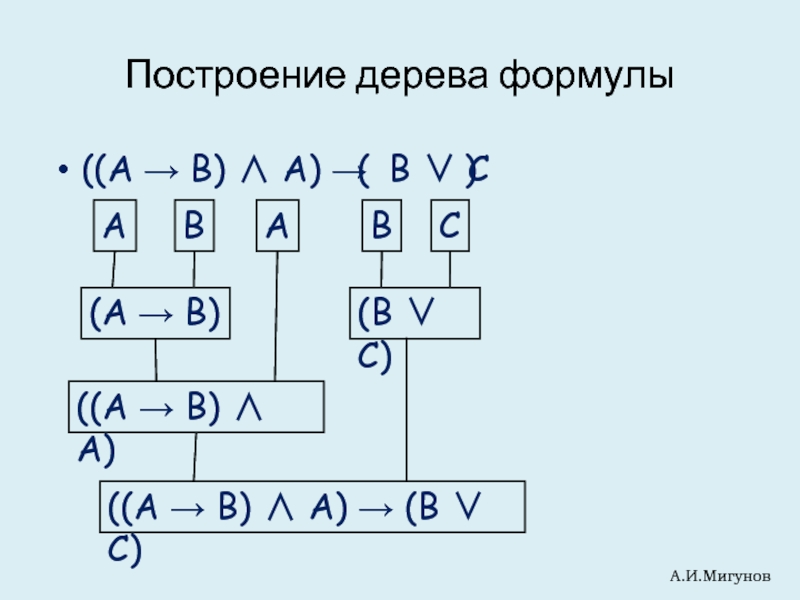
Слайд 5Построение дерева формулы
((A → B) ∧ A) → B ∨ C
(
)
С
А
В
А
В
(A
((A → B) ∧ A)
(B ∨ C)
((A → B) ∧ A) → (B ∨ C)
А.И.Мигунов
Слайд 7p q q
Студент A должен сдать все экзамены вовремя или взять академический отпуск, и, если он берет академический отпуск, то сможет продолжить обучение в следующем году.
Студент A должен сдать все экзамены вовремя - p
Студент A должен взять академический отпуск - q
Студент A сможет продолжить обучение в следующем году – t
∨
∧
→
(
)
(
)
Слайд 8Или Сэм пойдет на вечеринку, и Макс не пойдет на нее,
(p ∧ ∼ q) (∼ p ∧ r)
Необходимые и достаточные условия счастья для шейха состоит в том, чтобы иметь вино, женщин и услаждать свой слух пением.
p↔ (q ∧ r ∧ s)
Фиорелло ходит в кино только в том случае, когда там показывают комедию
(p → q)
Слайд 9Таблицы истинности формул логики высказываний
Некто А говорит: «Я лжец, а В
Кто А и кто В?
«А рыцарь» – А
«А лжец» - ∼А
∼А
∧
В
А.И.Мигунов
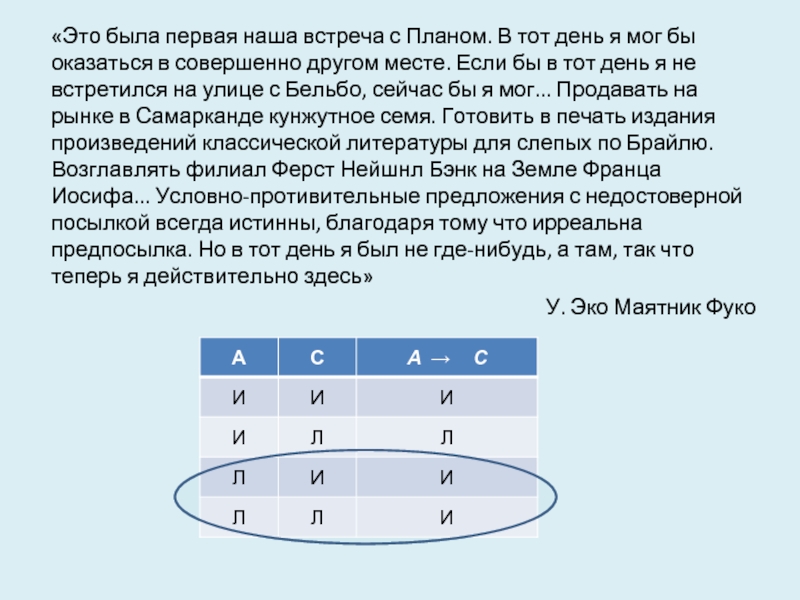
Слайд 11«Это была первая наша встреча с Планом. В тот день я
У. Эко Маятник Фуко
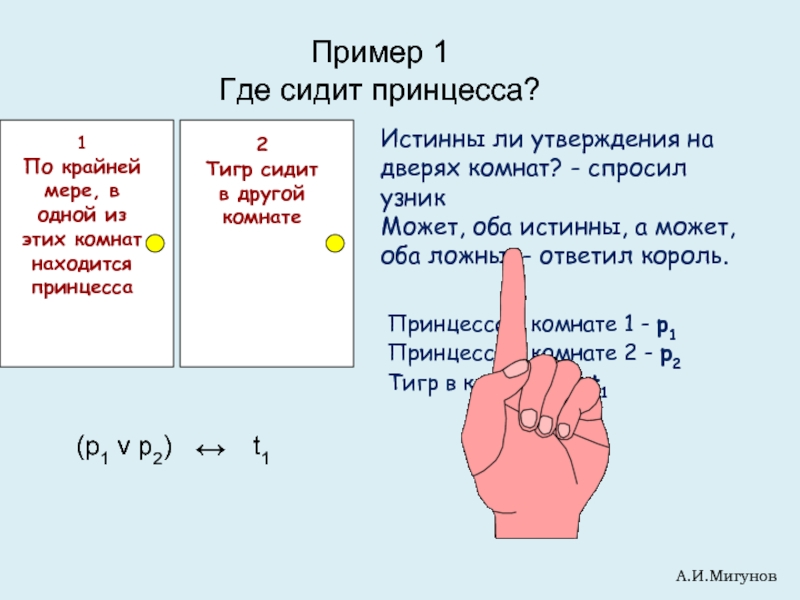
Слайд 14Пример 1
Где сидит принцесса?
Истинны ли утверждения на дверях комнат? - спросил
Может, оба истинны, а может, оба ложны, - ответил король.
Принцесса в комнате 1 - p1
Принцесса в комнате 2 - p2
Тигр в комнате 1 - t1
(p1 v p2) t1
↔
А.И.Мигунов
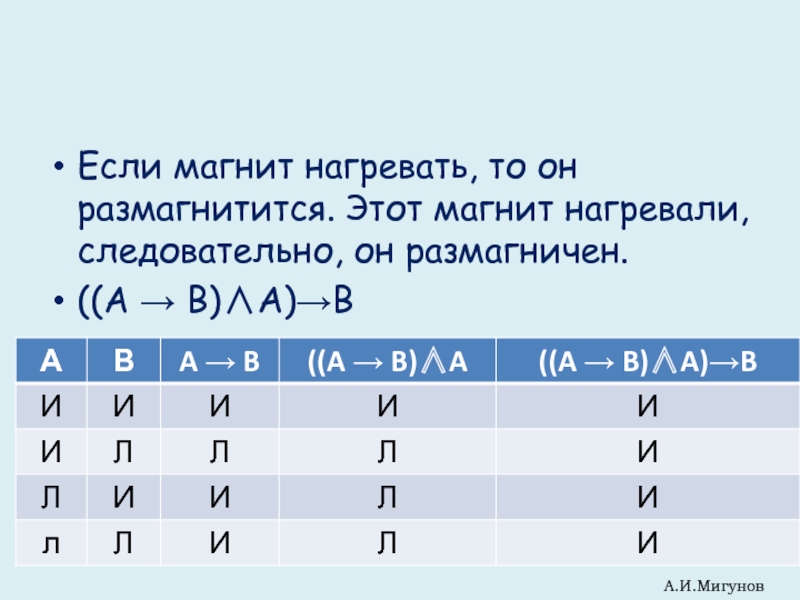
Слайд 16Если магнит нагревать, то он размагнитится. Этот магнит нагревали, следовательно, он
((A → B)∧A)→B
А.И.Мигунов
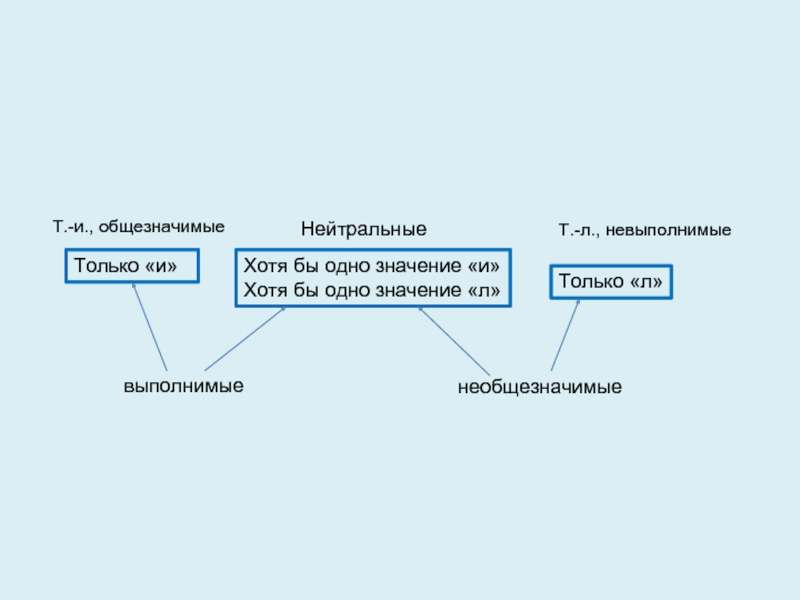
Слайд 17
Только «и»
Хотя бы одно значение «и»
Хотя бы одно значение «л»
Только «л»
Т.-и.,
Нейтральные
Т.-л., невыполнимые
выполнимые
необщезначимые
Слайд 18Отношение логического следования
Формула В логически следует из формул А1, А2,…, Аn
p → q
∼q
∼p
А1, А2├ В
А.И.Мигунов
Слайд 19Отношение логического следования
(Теорема дедукции)
Задача установления того, следует ли высказывание В из
А.И.Мигунов
Формула логики высказываний является тождественно-истинной формулой,
если при любых интерпретациях вхордящих в ее состав пропозициональных
переменных она принимает значение «истина».
Слайд 20
p → q
∼q
∼p
Отношение логического следования
Формула В логически следует из формул А1,
А1, А2├ В
(А1 ∧ А2)→ В
((p → q)∧∼q)→ ∼p
А.И.Мигунов
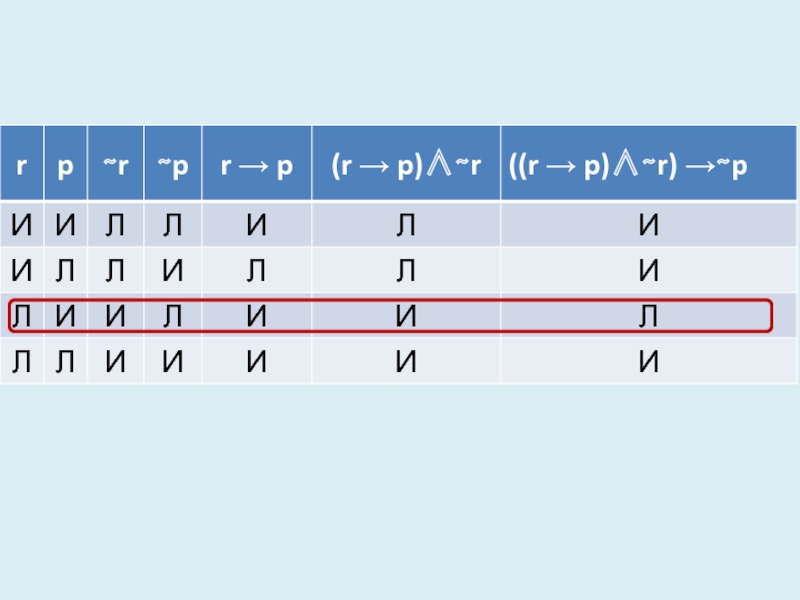
Слайд 24Я заплатил бы за работу по ремонту телевизора, если бы он
Я плачу за работу по ремонту телевизора – p
Телевизор работает - r
((r → p) ∧ ∼ r) → ∼ p
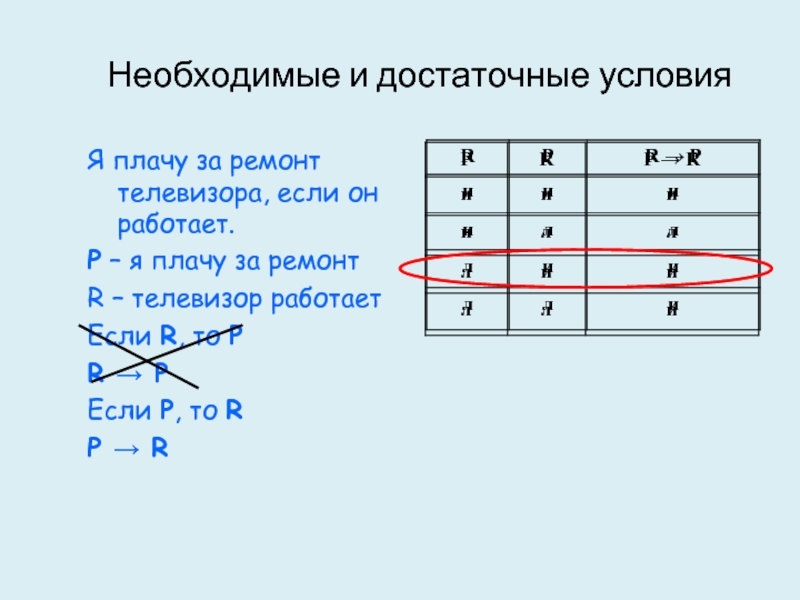
Слайд 26Необходимые и достаточные условия
Я плачу за ремонт телевизора, если он работает.
P
R – телевизор работает
Если R, то P
R → P
Если P, то R
P → R
Слайд 31«Если ваши книги согласуются с Кораном, то они излишни.
Если ваши книги
Но они либо согласуются с Кораном, либо нет.
Следовательно, они либо излишни, либо вредны»
А.И.Мигунов
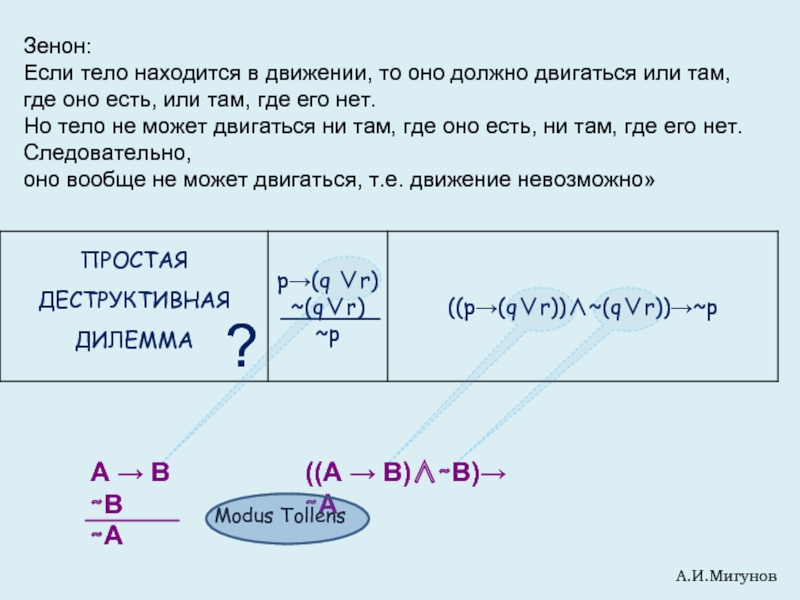
Слайд 32Зенон:
Если тело находится в движении, то оно должно двигаться или там,
где оно есть, или там, где его нет.
Но тело не может двигаться ни там, где оно есть, ни там, где его нет.
Следовательно,
оно вообще не может двигаться, т.е. движение невозможно»
?
A → B
∼B
∼A
((A → B)∧∼B)→ ∼A
А.И.Мигунов
Modus Tollens