- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Измерения в психологии презентация
Содержание
- 1. Измерения в психологии
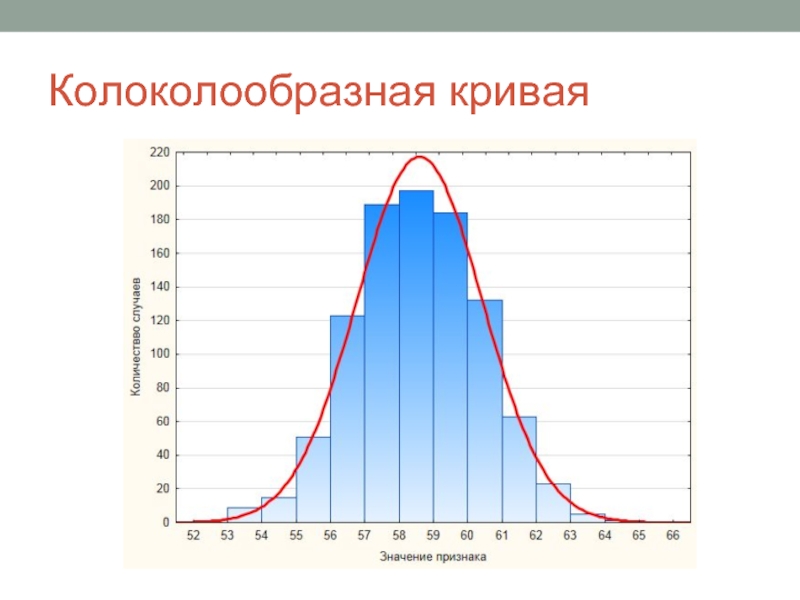
- 2. Колоколообразная кривая
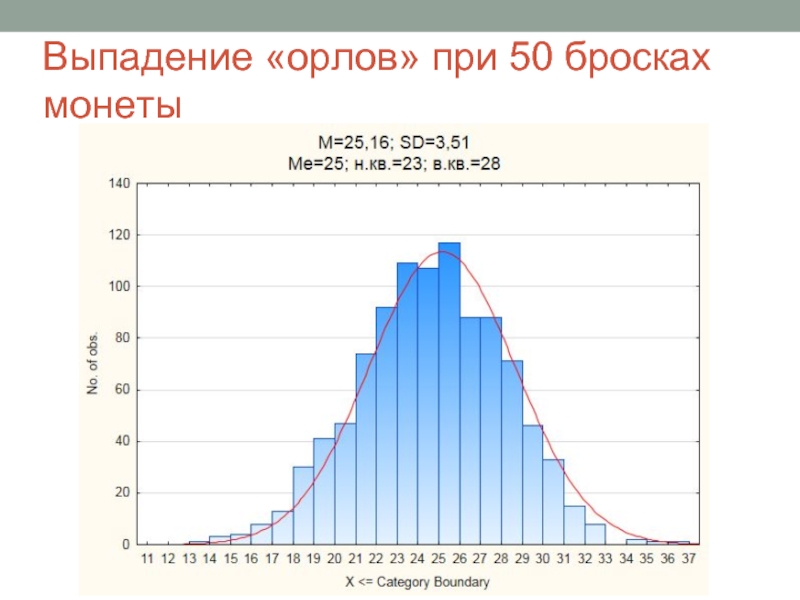
- 3. Выпадение «орлов» при 50 бросках монеты
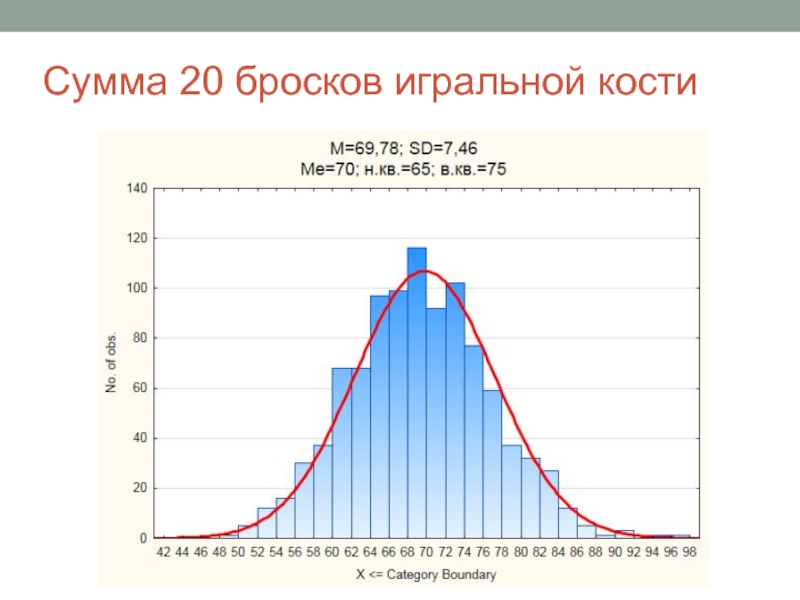
- 4. Сумма 20 бросков игральной кости
- 5. Свойство кривой нормального распределения
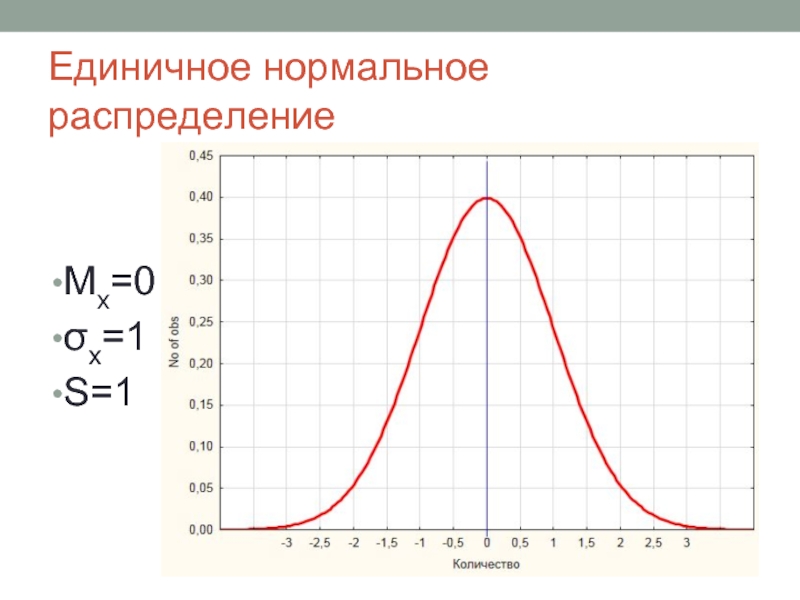
- 6. Единичное нормальное распределение Мх=0 σх=1 S=1
- 7. Формулы перехода между шкалами
- 8. Возможные причины отклонения от нормальности распределения Наличие
- 9. Виды отклонения от нормального распределения Асимметрия
- 10. Виды отклонения от нормального распределения Эксцесс –
- 11. Шкала стенов Стены (STAndart Ten) – «стандартная
- 12. Шкала стенов Мх=5,5 σх=2 СТЕНЫ Z-значения
- 13. Другие стандартные тестовые шкалы Шкала Векслера (шкала
- 14. Стандартная ошибка среднего
- 15. 95% доверительный интервал По свойствам нормального распределения
- 16. Пример: истинное среднее лежит в пределах 95%
- 17. Пример: истинное среднее лежит за пределами 95%
- 18. Наиболее распространенные доверительные интервалы 95% доверительный интервал
- 19. Взаимосвязь между признаками
Слайд 8Возможные причины отклонения
от нормальности распределения
Наличие большого количества выбросов;
Погрешность измерения (шкала перестала
быть метрической);
NB! Если шкала перестала быть метрической, она все равно остается количественной – а именно, ранговой, так как по-прежнему обладает всеми ее свойствами.
Влияние неучтенной (побочной) переменной.
NB! Если шкала перестала быть метрической, она все равно остается количественной – а именно, ранговой, так как по-прежнему обладает всеми ее свойствами.
Влияние неучтенной (побочной) переменной.
Слайд 9Виды отклонения от нормального распределения
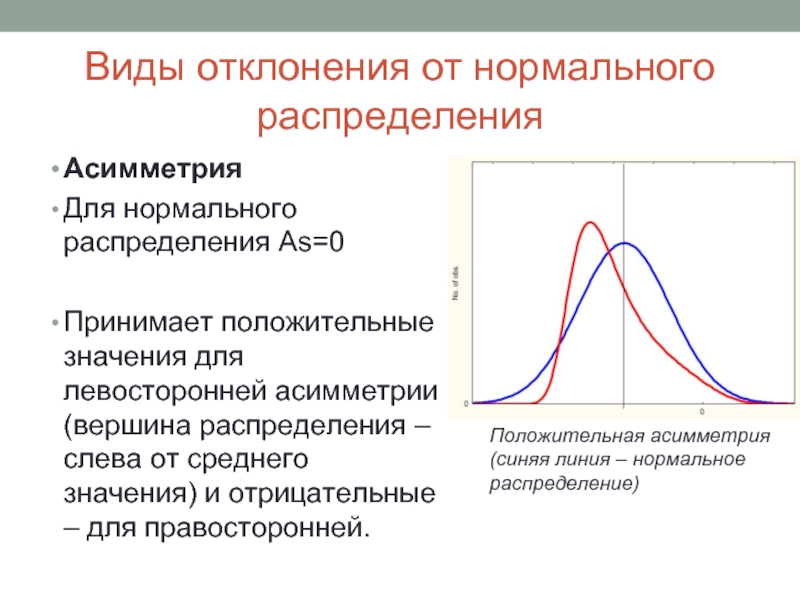
Асимметрия
Для нормального распределения As=0
Принимает положительные значения
для левосторонней асимметрии (вершина распределения – слева от среднего значения) и отрицательные – для правосторонней.
Положительная асимметрия
(синяя линия – нормальное распределение)
Слайд 10Виды отклонения от нормального распределения
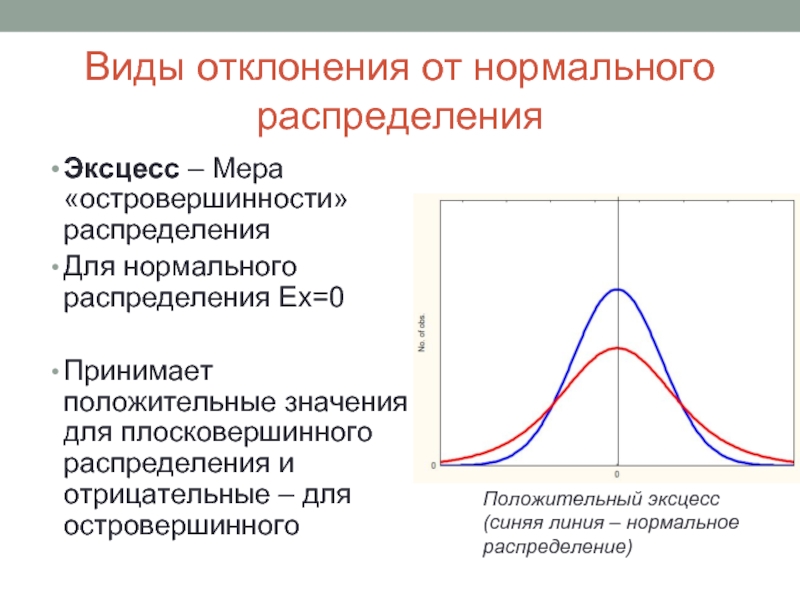
Эксцесс – Мера «островершинности» распределения
Для нормального распределения
Ex=0
Принимает положительные значения для плосковершинного распределения и отрицательные – для островершинного
Принимает положительные значения для плосковершинного распределения и отрицательные – для островершинного
Положительный эксцесс
(синяя линия – нормальное распределение)
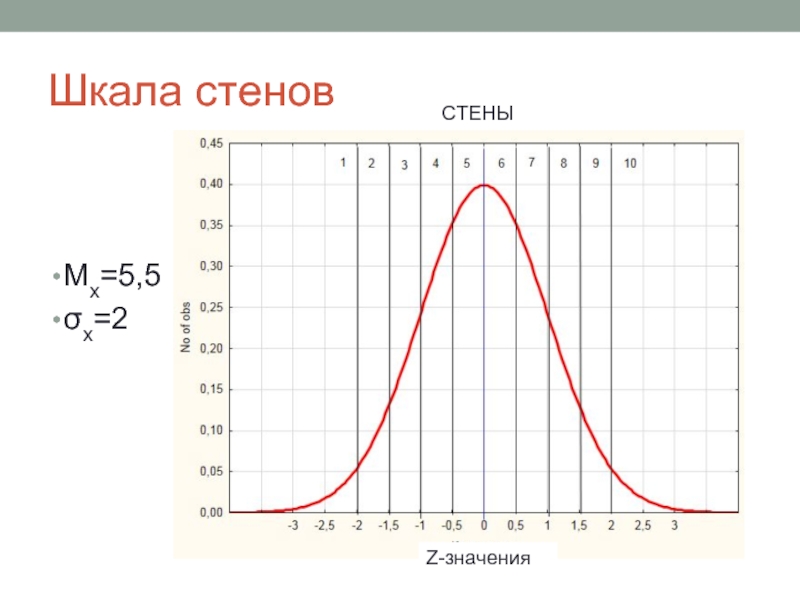
Слайд 11Шкала стенов
Стены (STAndart Ten) – «стандартная десятка». Шкала состоит из 10
возможных целых значений (от 1 до 10), для которой Мх=5,5 и σх=2.
Дробные значения округляются до целых.
Пользуясь формулами перехода между шкалами, любой признак, имеющий примерно нормальное распределение, можно выразить в стенах.
Дробные значения округляются до целых.
Пользуясь формулами перехода между шкалами, любой признак, имеющий примерно нормальное распределение, можно выразить в стенах.
Слайд 13Другие стандартные тестовые шкалы
Шкала Векслера (шкала IQ):
Мх=100
σх=15
Шкала Т-баллов:
Мх=50
σх=10
Слайд 1595% доверительный интервал
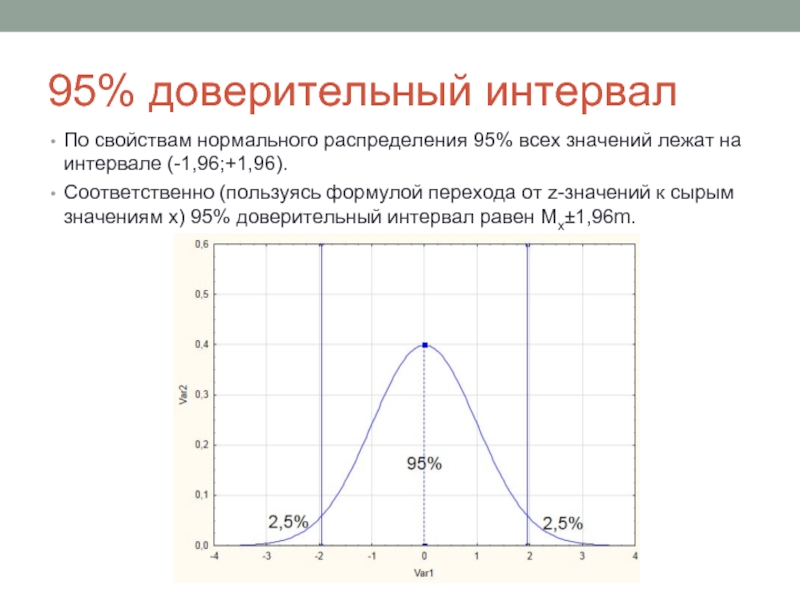
По свойствам нормального распределения 95% всех значений лежат на
интервале (-1,96;+1,96).
Соответственно (пользуясь формулой перехода от z-значений к сырым значениям х) 95% доверительный интервал равен Мх±1,96m.
Соответственно (пользуясь формулой перехода от z-значений к сырым значениям х) 95% доверительный интервал равен Мх±1,96m.
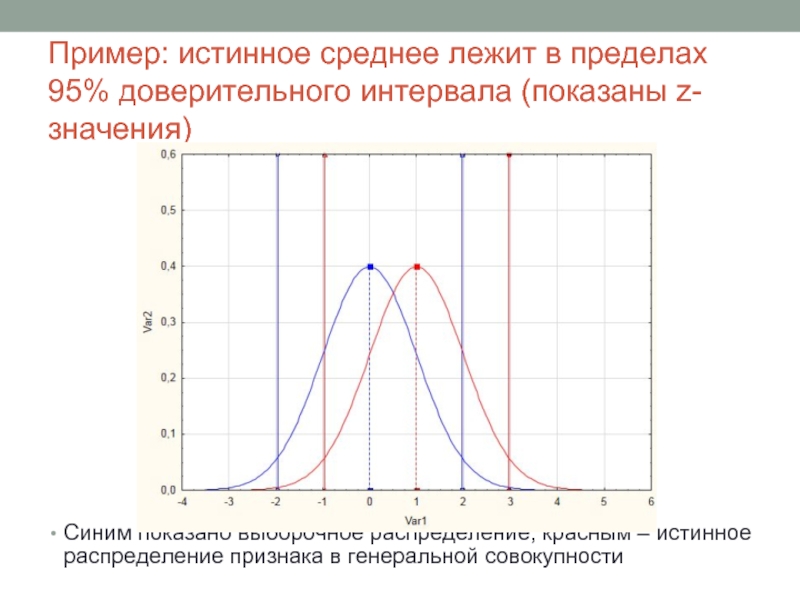
Слайд 16Пример: истинное среднее лежит в пределах 95% доверительного интервала (показаны z-значения)
Синим
показано выборочное распределение, красным – истинное распределение признака в генеральной совокупности
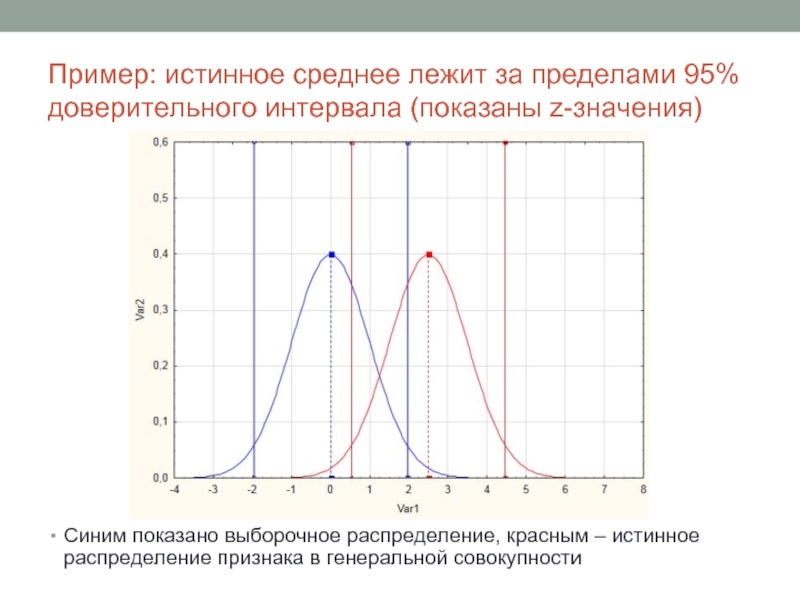
Слайд 17Пример: истинное среднее лежит за пределами 95% доверительного интервала (показаны z-значения)
Синим
показано выборочное распределение, красным – истинное распределение признака в генеральной совокупности
Слайд 18Наиболее распространенные доверительные интервалы
95% доверительный интервал равен Мх±1,96m.
99% доверительный интервал примерно
соответствует Мх±2,58m (точнее, Мх±2,575m).
90% доверительный интервал примерно соответствует Мх±1,64m.
90% доверительный интервал примерно соответствует Мх±1,64m.