- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическое изучение динамики презентация
Содержание
- 1. Статистическое изучение динамики
- 2. Ряды динамики (хронологические, временные) - ряды
- 3. Уровень ряда динамики – это размер (величина,
- 4. Интервал - В моментном ряду динамики– это
- 5. Виды рядов динамики в зависимости от способа
- 6. При составлении ряда динамики : проводят
- 7. Периодизация может осуществляться несколькими методами: Исторический
- 8. Анализа рядов динамики позволяет: — дать представление
- 9. Показатели анализа рядов динамики абсолютный прирост
- 10. Показатели анализа рядов динамики рассчитывают как
- 11. Абсолютный прирост Цепной: Δiцеп =Yi—Yi-1
- 12. Коэффициент роста: Цепной: Базисный:
- 13. Темпы роста : Тр =Кр *100
- 14. Абсолютное содержание 1% прироста: Или А= Yi-1 :100
- 15. Средний уровень ряда динамики: Моментного: Интервального:
- 16. При анализе социально-экономических явлений во времени выявляют
- 17. Тренд — это долговременная компонента ряда динамики,
- 18. Проверка на наличие тренда в ряду динамики
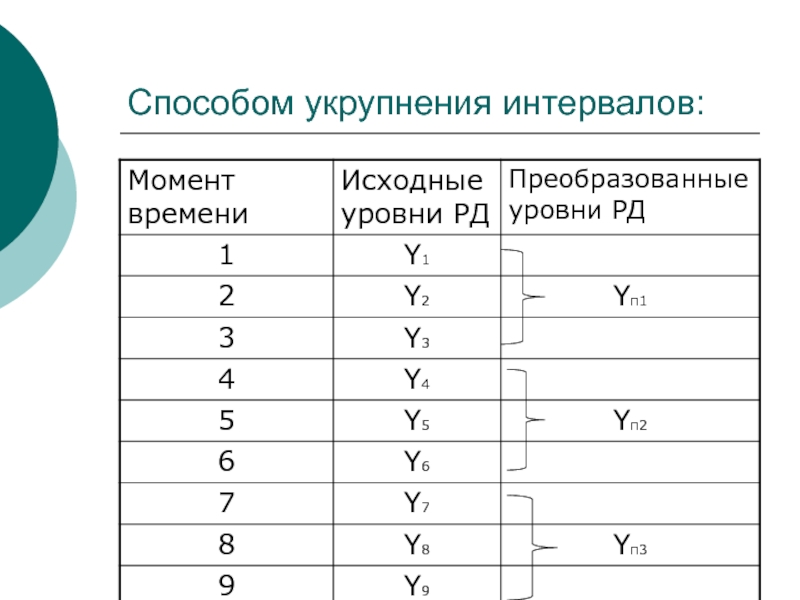
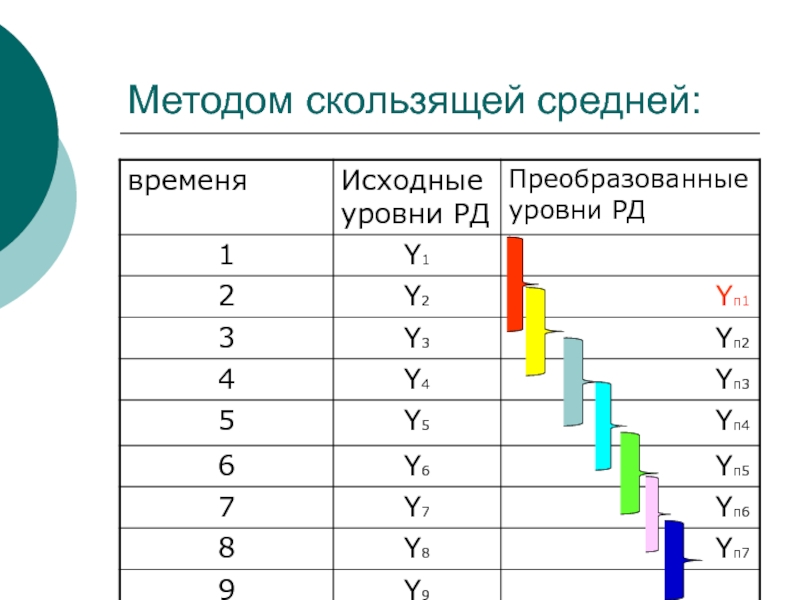
- 19. Выделение тренда проводят: Способом укрупнения интервалов Методом скользящей средней Методом аналитического выравнивания
- 20. Способом укрупнения интервалов:
- 21. Методом скользящей средней:
- 22. При аналитическом выравнивании используются следующие зависимости: линейная:
- 23. Для оценки параметров (а0, а1, а2,...) используют:
- 24. Yt=a0+a1tt. Yt - значения выравненного
- 25. система нормальных уравнений:
- 26. Оценку надежности уравнения регрессии проводят на основе
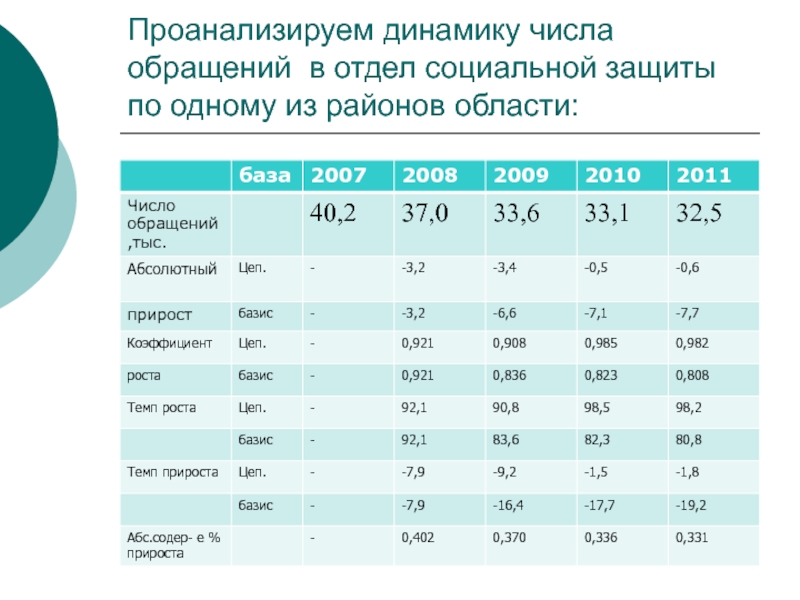
- 27. Проанализируем динамику числа обращений в отдел социальной защиты по одному из районов области:
- 28. Среднегодовые показатели динамики: Средний абсолютный прирост: по
- 29. Средний уровень ряда динамики: определяем по формуле средней арифметической простой (ряд интервальный):
- 30. Среднегодовые показатели ряда динамики используют для прогноза:
- 31. На основе относительных показателей (Кр): б) умножая
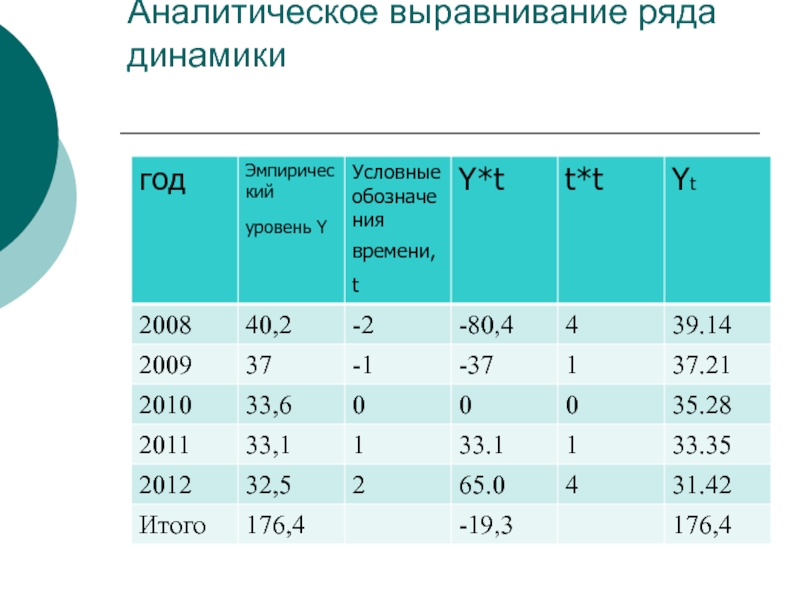
- 32. Аналитическое выравнивание ряда динамики
- 33. Параметры и уравнение тренда: из первого уравнения
- 34. Сезонные колебания - колебание уровней ряда
- 35. Уровень сезонности оценивается с помощью: индексов сезонности:
- 36. Индексы сезонности: Если тренда нет или
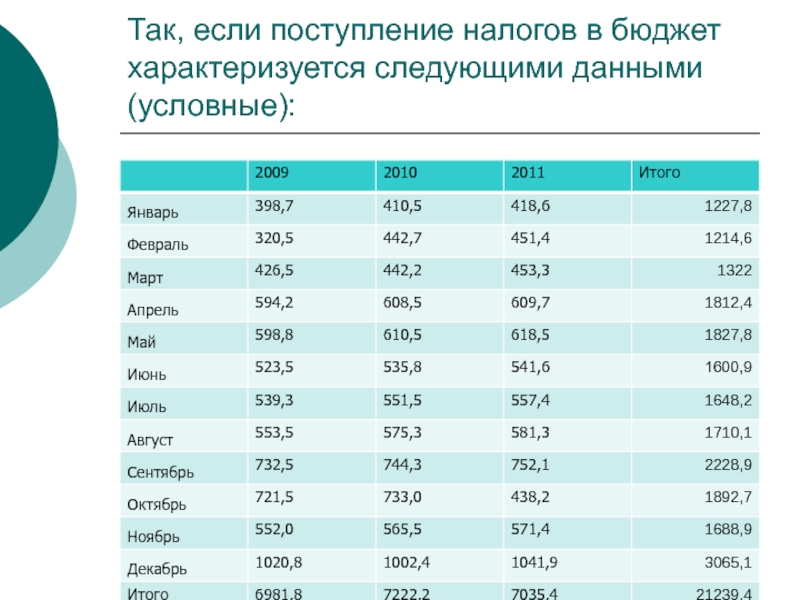
- 37. Так, если поступление налогов в бюджет характеризуется следующими данными (условные):
- 38. Таблица по расчету индексов сезонности
- 39. Последовательность расчета индекса сезонности определяем средний
- 40. Гармонический анализ выполняют представляя временной ряд как
- 41. Индекс – относительная величина, показывающая, во
- 42. Различие условий может проявляться -во времени (индексы
- 43. Различают: Индивидуальные индексы Общие (агрегатные) индексы Индексы
- 44. Индивидуальные индексы- относительная величина, получаемая при сравнении
- 45. Общие (агрегатные) индексы Относительные величины в виде
- 46. Соответственно, общие индексы- Цен- соотношение товарооборота отчетного
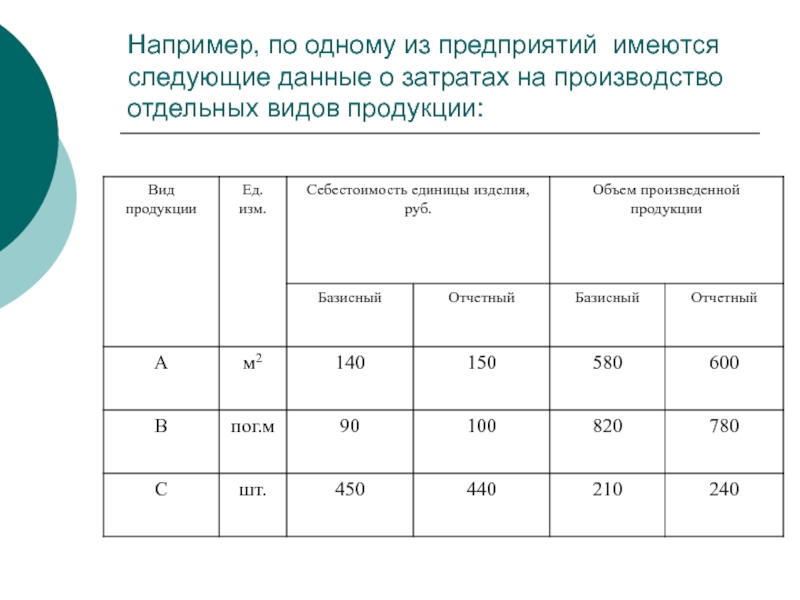
- 47. Например, по одному из предприятий имеются следующие данные о затратах на производство отдельных видов продукции:
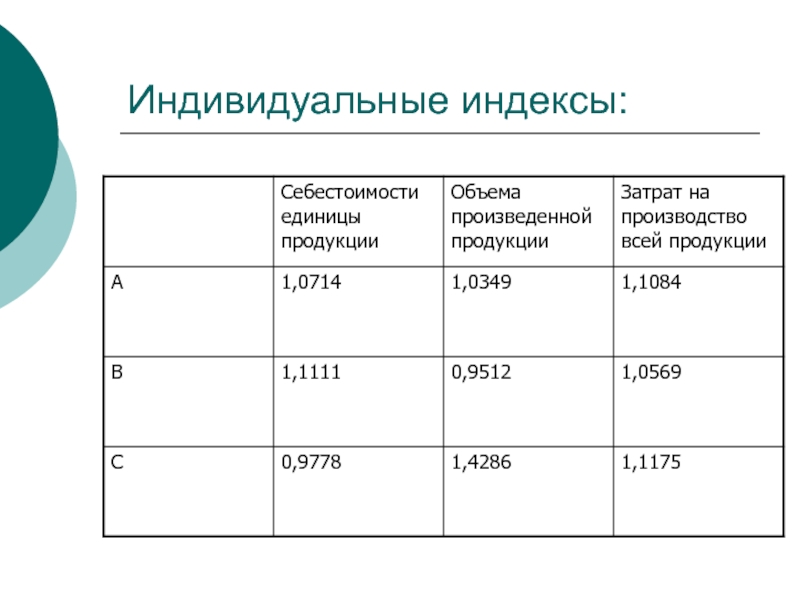
- 48. Индивидуальные индексы:
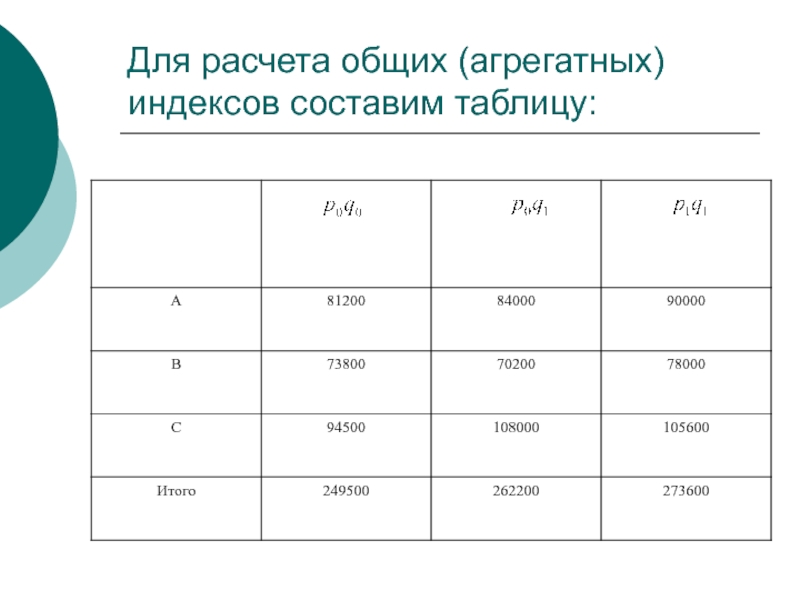
- 49. Для расчета общих (агрегатных) индексов составим таблицу:
- 50. Агрегатные индексы: Затрат: Себестоимости единицы
- 51. Разностное сравнение числителя и знаменателя индексов показывает
- 52. Индексы средних величин индекс переменного состава -отношение
- 53. индекс постоянного (или фиксированного) состава Агрегатный индекс,
- 54. Индекс структурных изменений
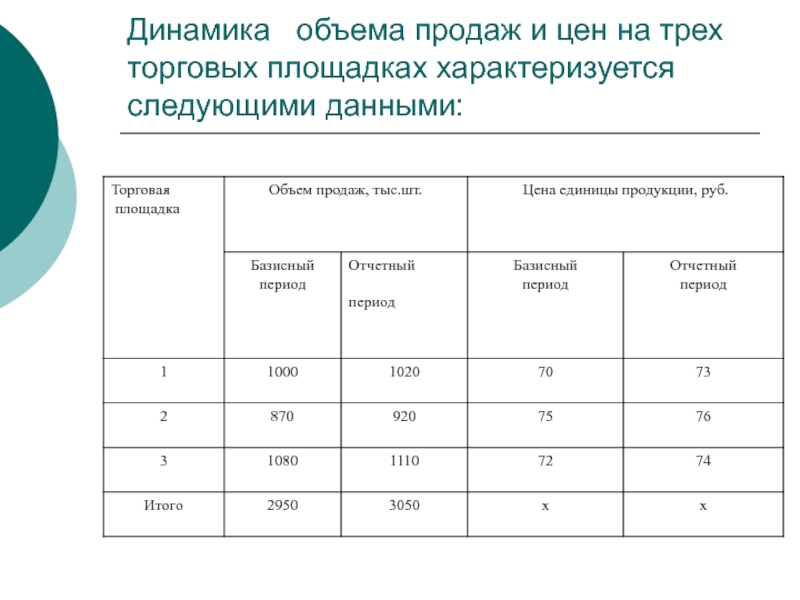
- 55. Динамика объема продаж и цен на трех торговых площадках характеризуется следующими данными:
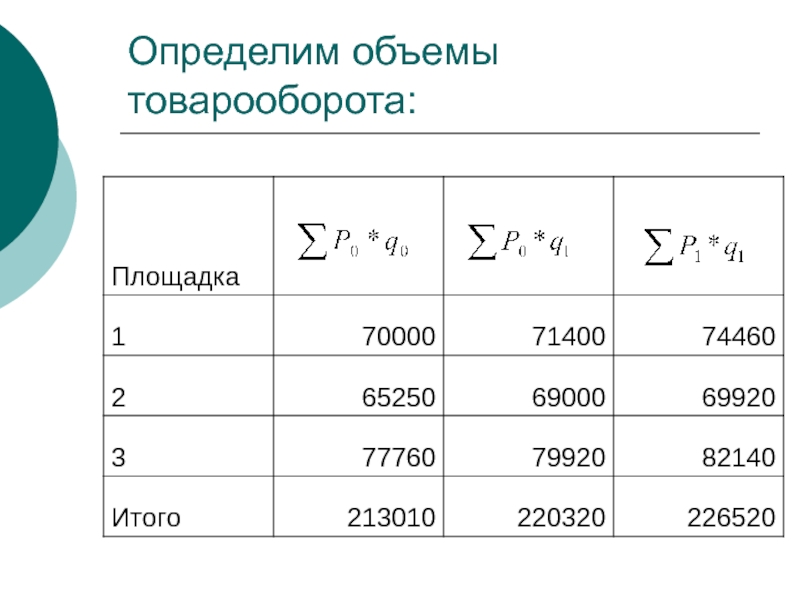
- 56. Определим объемы товарооборота:
- 57. Индексы Переменного состава: Постоянного состава: Структурных сдвигов:
- 58. Индексы общего объема товарооборота может быть рассчитан
- 59. Индекс физического объема товарооборота может быть рассчитан
- 60. Индекс цен рассчитывают как индекс средний из
- 61. Имеются следующие данные о динамике товарооборота, цен и физического объема проданных товаров:
- 62. Индекс товарооборота может быть определен по формуле
- 63. Индексы изменения общей суммы товарооборотав связи с
- 64. Территориальные индексы - это разновидность относительных величин
- 65. Построение территориальных индексов товарооборота – это
- 66. Территориальные индексы физического объема товарооборота цен
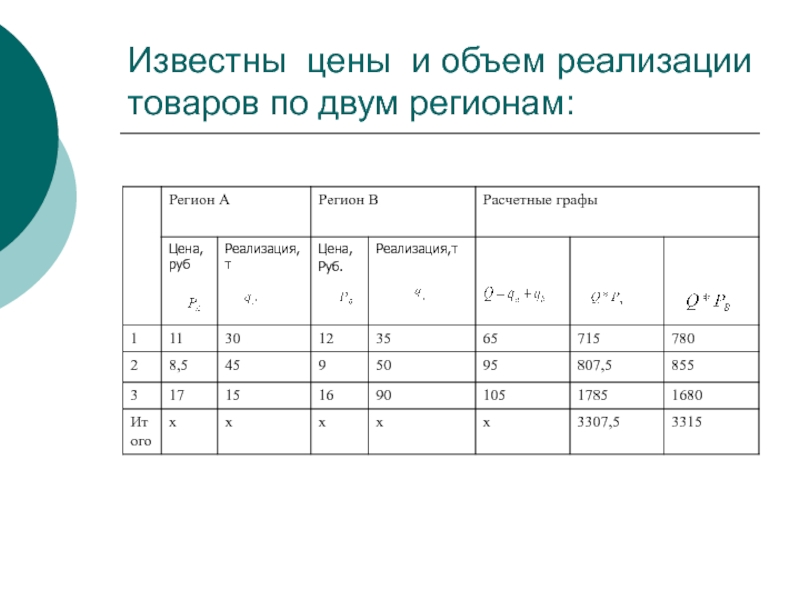
- 67. Известны цены и объем реализации товаров по двум регионам:
- 68. Территориальные индексы товарооборота: цен: Цены в
Слайд 1 Статистическое изучение динамики
1.Динамические ряды: их виды, правила построения и
2. Показатели анализа рядов динамики. Средние показатели в рядах динамики
3. Методы выравнивания рядов динамики и выявления тенденции ряда.
4. Индексы в оценке динамики и взаимосвязей. Стандартизация.
Слайд 2Ряды динамики (хронологические, временные) -
ряды изменяющихся во времени значений статистических
Составными элементами рядов динамики являются:
- цифровые значения изучаемого показателя - уровни ряда динамики (У);
- периоды (или моменты) времени, к которым они относятся (t).
Слайд 3Уровень ряда динамики –
это размер (величина, объем) того или иного явления
Элементами времени могут быть:
- моменты (начало, конец года, квартала, месяца и т.п.) времени –моментный ряд
- периоды (год, квартал, месяц, сутки и т.п.) времени – интервальный ряд
Слайд 4Интервал -
В моментном ряду динамики– это промежуток времени между датами учета
В интервальном ряду – тот же промежуток времени, за который обобщены приводимые сведения, когда они накапливались.
Слайд 5Виды рядов динамики
в зависимости от способа выражения уровней ряды динамики (
в зависимости от характера приводимых показателей (моментные и интервальные ряды динамики)
в зависимости от расстояния между уровнями (полные и неполные)
в зависимости от числа показателей (изолированные и комплексные)
в зависимости от наличия основной тенденции изучаемого процесса (стационарные и нестационарные )
Слайд 6При составлении ряда динамики :
проводят периодизацию развития явления
приводят к
решают вопрос о величине временных интервалов
упорядочивают уровни рядов динамики во времени
Слайд 7Периодизация может осуществляться несколькими методами:
Исторический метод
Метод параллельной периодизации
Методы многомерного статистического
Слайд 8Анализа рядов динамики позволяет:
— дать представление об изменениях показателей за прошедший
— охарактеризовать интенсивность отдельных изменений;
— определить средние показатели временного ряда;
— выявить основные тенденции и закономерности изменений изучаемого явления;
— выявить факторы, обусловливающие изменение явления во времени;
— осуществить прогноз о возможном уровне явления на перспективу
Слайд 9Показатели анализа рядов динамики
абсолютный прирост
темп роста
темп прироста
абсолютное значение
Система средних показателей динамики:
средний уровень ряда,
средние показатели анализа рядов динамики
Слайд 11Абсолютный прирост
Цепной: Δiцеп =Yi—Yi-1
Базисный:
Средний:
на основе цепных абсолютных приростов:
на основе базисного абсолютного прироста:
Слайд 16При анализе социально-экономических явлений во времени выявляют три компонента динамики:
-
- систематические и кратковременные изменения (сезонные колебания);
- несистематические случайные колебания, которые часто обусловлены субъективными и иными частными причинами
Слайд 17Тренд —
это долговременная компонента ряда динамики, выражающая длительную, ведущую тенденцию развития
Изучение тенденции ряда включает два основных этапа:
ряд динамики проверяется на наличие тренда;
производится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов
Слайд 18Проверка на наличие тренда в ряду динамики может быть осуществлена:
- методом
- фазочастотным критерием знаков первой разности (Валлиса и Мура);
- критерием Кокса и Стюарта.
- методом серий
Слайд 19Выделение тренда проводят:
Способом укрупнения интервалов
Методом скользящей средней
Методом аналитического выравнивания
Слайд 22При аналитическом выравнивании используются следующие зависимости:
линейная:
- параболическая:
экспоненциальные:
Слайд 23Для оценки параметров (а0, а1, а2,...) используют:
метод наименьших квадратов, который обеспечивает
Слайд 24Yt=a0+a1tt.
Yt - значения выравненного ряда, которые необходимо вычислить;
t - показатель
а0, и a1 - параметры прямой, определенные из системы нормальных уравнений:
Слайд 26Оценку надежности уравнения регрессии проводят на основе
критерия Фишера (F) - при
Слайд 27Проанализируем динамику числа обращений в отдел социальной защиты по одному из
Слайд 28Среднегодовые показатели динамики:
Средний абсолютный прирост:
по базисным - (-7,7)/4=-1,9 (тыс. ) или
по
Средний коэффициент роста:
по базисным -
по цепным –
Средний темп роста:
Средний темп прироста:
Слайд 29Средний уровень ряда динамики:
определяем по формуле средней арифметической простой (ряд интервальный):
Слайд 30Среднегодовые показатели ряда динамики используют для прогноза:
а) прибавляя последовательно к последнему
Yn+t - - экстраполируемый уровень ряда динамики,
n+t - номер этого уровня (года);
n - номер конечного уровня (года) периода, за который рассчитан среднегодовой абсолютный прирост
t - срок прогноза (период упреждения)
Таким образом, ожидаемое число обращенийй через два года составит:
32,5+ 2*(-1,9)=28,7 (тыс. человек)
Слайд 31На основе относительных показателей (Кр):
б) умножая уровень ряда динамики на среднегодовой
ожидаемое число обращений населения через два года составит:
32,5*0,948*0,948= 29,2 (тыс.человек).
Слайд 33Параметры и уравнение тренда:
из первого уравнения системы определяют а0 –средний уровень
из второго уравнения системы определяем а1:
уравнение тренда: Yt=35,28-1,93t,
через два года (t=4) ожидается, что число обращений в районе составит: 35,28-1,93*4=27,56 (тыс.)
Слайд 34Сезонные колебания -
колебание уровней ряда динамики, возникающие под влиянием смены
Слайд 35Уровень сезонности оценивается с помощью:
индексов сезонности:
2) метода гармонического анализа
Слайд 36Индексы сезонности:
Если тренда нет или он незначителен, то для каждого
где Yt – средний уровень показателя за месяц (квартал t);
Yср - общий средний уровень показателя
Если тенденция имеется, то сначала проводят аналитическое выравнивание, а затем рассчитывают индекс сезонности по формуле:
где -выровненный уровень
Слайд 39Последовательность расчета индекса сезонности
определяем средний размер поступлений налогов за каждый
так, в январе (398,7+410,5+418,6):3=1227,8:3=409,3
определяем средний размер поступлений налогов в среднем за период:
(6981,8+7222,2+7035,2):36=21239,4:36=590,0
Индекс сезонности:
409,3:590,0=0,694 (т.е. в январе поступило налогов 69,4% от среднемесячного уровня
Слайд 40Гармонический анализ
выполняют представляя временной ряд как сумму периодических колебательных процессов
где
f (t) - выровненный уровень или трендовое значение ряда в тот же момент (интервал) времени
- параметры колебательного процесса (гармоники) с номером
Слайд 41Индекс –
относительная величина, показывающая, во сколько раз уровень изучаемого явления
Слайд 42Различие условий может проявляться
-во времени (индексы динамики)
-в пространстве (территориальные индексы)
-в выборе в качестве базы сравнения какого-либо условного уровня (например, структуру той или иной группы населения – стандартизованные индексы, планового уровня –индексы планового задания, выполнения плана)
Слайд 43Различают:
Индивидуальные индексы
Общие (агрегатные) индексы
Индексы средних величин
Средние из индивидуальных (средний арифметический,
Территориальные индексы
Слайд 44Индивидуальные индексы-
относительная величина, получаемая при сравнении уровней, например,
товарооборота:
Физ-го объема товарооборота:
цен
Причем,
где i – обозначение индивидуального индекса
q. p- индексируемые величины
1 и 0 –обозначение уровней отчетного и базисного периода соответственно
Слайд 45Общие (агрегатные) индексы
Относительные величины в виде сравнения агрегатов (сумм произведений взвешивающего
Слайд 46Соответственно, общие индексы-
Цен- соотношение товарооборота отчетного периода с товарооборотом отчетного периода
Физического объема- соотношение товарооборота отчетного периода в сопоставимых ценах с товарооборотом базисного периода:
Слайд 47Например, по одному из предприятий имеются следующие данные о затратах на
Слайд 51Разностное сравнение числителя и знаменателя индексов показывает прирост затрат:
Общей суммы:
на 273600
вследствие изменения себестоимости единицы продукции:
на 273600-262200=11400 ( рублей )
вследствие изменения физического объема:
на 262200-249500=12700 ( рублей )
24100=11400+12700
Слайд 52Индексы средних величин
индекс переменного состава -отношение двух средних величин (учитывает
Слайд 53индекс постоянного (или фиксированного) состава
Агрегатный индекс, полученный по типу индекса цен
Слайд 54Индекс структурных изменений
где do – удельные веса, доли предприятий в общем
d1 – удельные веса или доли каждого предприятия в общем объеме выпускаемой продукции в отчетном периоде:
do = q0 / Σq0, d1 = q1 / Σq1.
Между индексом переменного состава, постоянного состава и структурных сдвигов существует соотношение
Iпер.сост = Iстр *Iпост.сос
Слайд 58Индексы общего объема товарооборота может быть рассчитан как индекс средний из
по форме среднего арифметического индекса:
по форме средней гармонической величины
Слайд 59Индекс физического объема товарооборота может быть рассчитан как индекс средний из
по форме среднего арифметического индекса:
Слайд 60Индекс цен рассчитывают как индекс средний из индивидуальных
по форме средней гармонической
Слайд 61Имеются следующие данные о динамике товарооборота, цен и физического объема проданных
Слайд 62Индекс товарооборота может быть определен по формуле
Агрегатного индекса:
среднего арифметического индекса:
средней гармонического
объем продаж в фактически действовавших ценах увеличился на 4,4% или на 241,5 тыс.руб
Слайд 63Индексы изменения общей суммы товарооборотав связи с изменением
физического объема:
в связи
1,044=1,031*1,012
Слайд 64Территориальные индексы -
это разновидность относительных величин сравнения, когда сопоставляются сложные показатели,
Слайд 65Построение территориальных индексов
товарооборота – это отношение суммы выручки от продажи
Слайд 66Территориальные индексы
физического объема товарооборота
цен
где р – средняя межрайонная цена
q– суммарный по двум районам объем продаж каждого вида товара.
Слайд 68Территориальные индексы
товарооборота:
цен:
Цены в регионе В на 0,2% превышают цены региона А.
физического
необходимо рассчитать средние цены по каждому товару:
=(11,0*30+12,0*35)/65=11,54;