- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчет текущего и страхового запаса презентация
Содержание
- 1. Расчет текущего и страхового запаса
- 2. Методы расчета текущего и страхового запаса могут
- 3. Общие зависимости для расчета норм запасов
- 6. Если величины и , выражены в
- 7. Принципиально другой подход в оценке времени и
- 8. Пример 9.1. Рассчитаем норму текущего и страхового
- 10. Определим статистические характеристики параметров поставки и расхода
- 12. Средний интервал между поставками: Среднее квадратическое
- 13. Средний интервал между требованиями: Среднее квадратическое
- 15. Расчет показал, что норма текущего запаса, рассчитанная
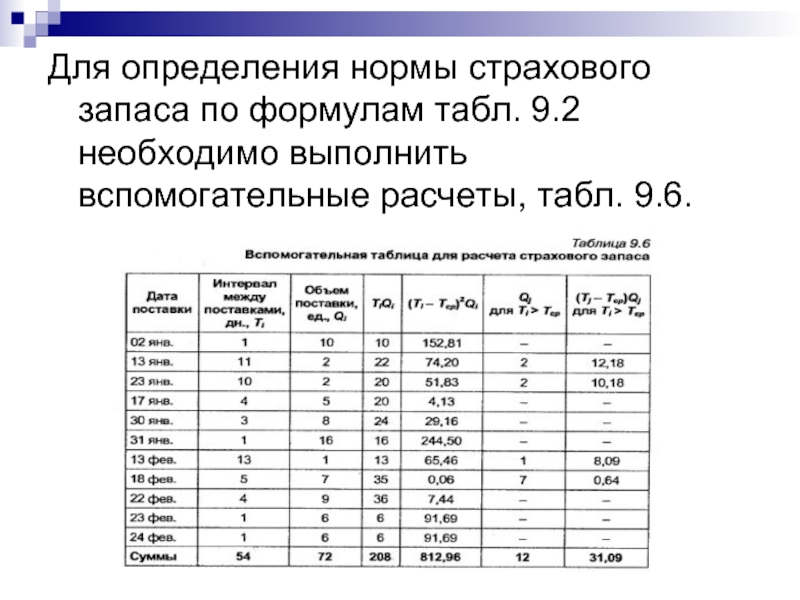
- 16. Для определения нормы страхового запаса по формулам табл. 9.2 необходимо выполнить вспомогательные расчеты, табл. 9.6.
- 17. Таким
- 18. Пример 9.2. Рассчитаем норму текущего и страхового
- 19. На основе имеющихся данных смоделируем процесс поставки
- 20. Если условие не соблюдается (не наблюдается дефицита),
- 21. Разница по существу, представляет
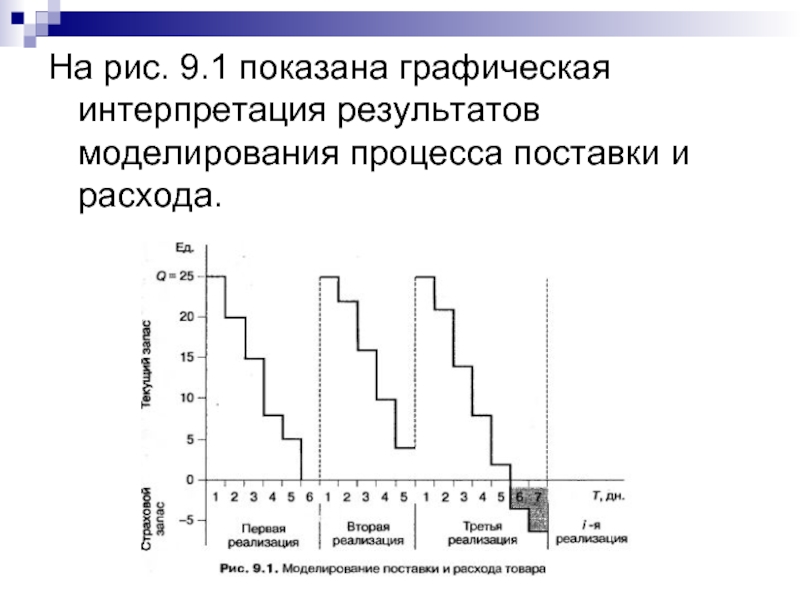
- 22. На рис. 9.1 показана графическая интерпретация результатов моделирования процесса поставки и расхода.
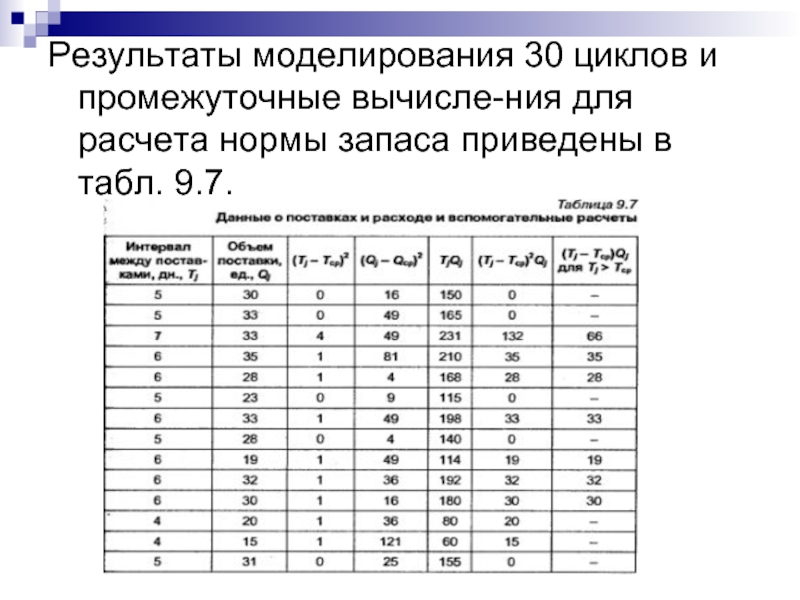
- 23. Результаты моделирования 30 циклов и промежуточные вычисления
- 25. По результатам моделирования получили: средний интервал
- 26. Расчет нормы текущего и страхового запаса по
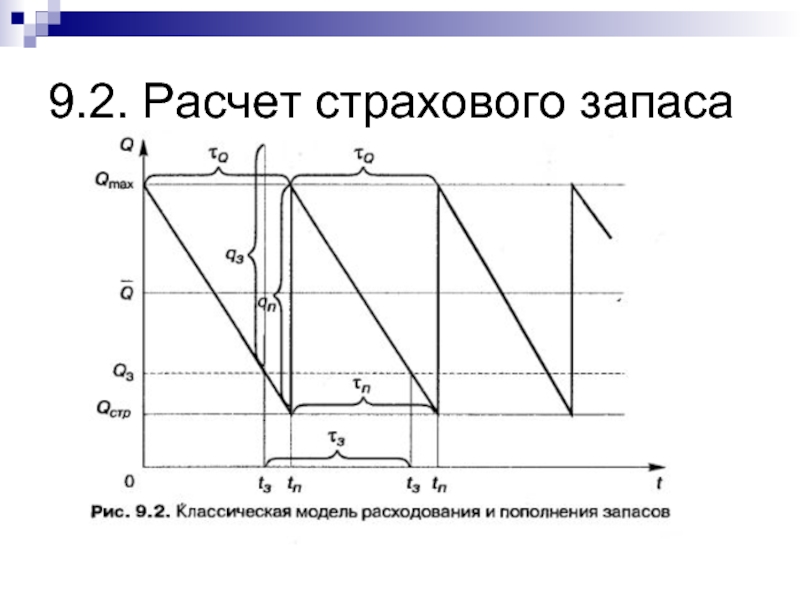
- 28. 9.2. Расчет страхового запаса
- 30. 5. Если в момент времени суммарный
- 31. Для расчета величины страхового запаса в условиях
- 33. Функция рассчитывается по формуле
Слайд 2Методы расчета текущего и страхового запаса могут быть разделены на три
группы:
методы, основанные на обработке статистических данных;
аналитические методы;
имитационное моделирование и последующая обработка результатов.
методы, основанные на обработке статистических данных;
аналитические методы;
имитационное моделирование и последующая обработка результатов.
Слайд 6Если величины и , выражены в днях, то для расчета
нормы текущего и страхового запаса в натуральном выражении используются зависимости:
где - среднесуточная потребность. ед./дн.
где - среднесуточная потребность. ед./дн.
Слайд 7Принципиально другой подход в оценке времени и размера текущего запаса, приведенный
в разделе 8 (формула Уилсона), базируется не только на данных наблюдений за поставками (расходами), но и на экономических показателях. С учетом формул раздела 8 норма текущего запаса запишется в виде (в днях):
(9.3)
В натуральных единицах:
(9.4)
(9.3)
В натуральных единицах:
(9.4)
Слайд 8Пример 9.1.
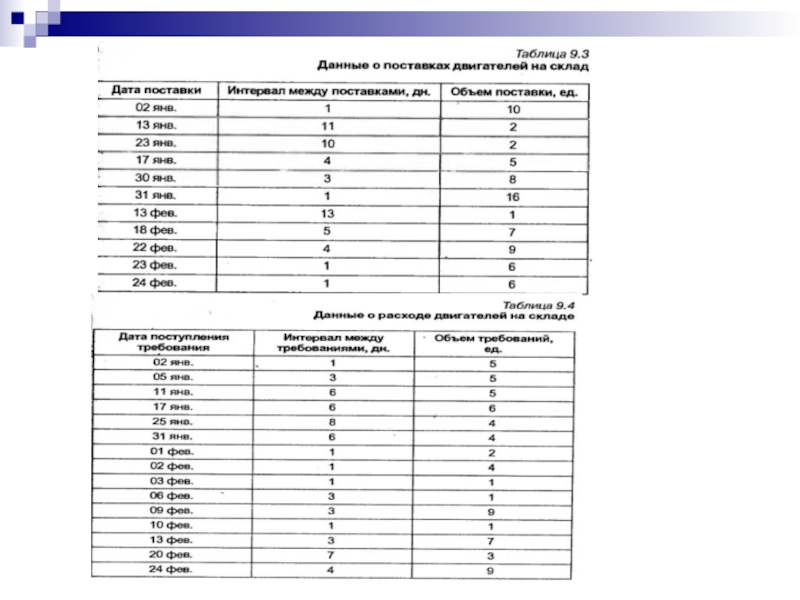
Рассчитаем норму текущего и страхового запаса по данным о поставке
и расходе двигателей на складе автотранспортного предприятия, табл 9.3 и 9.4
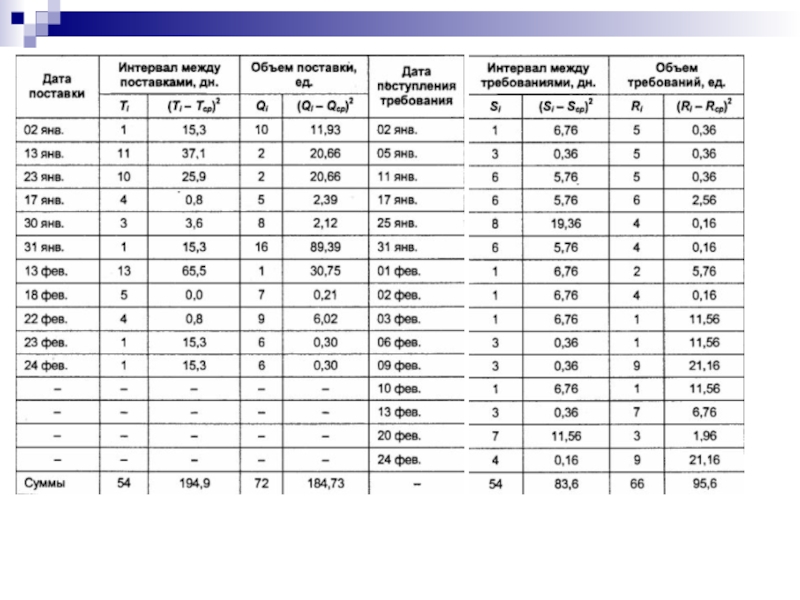
Слайд 10Определим статистические характеристики параметров поставки и расхода двигателей. Вспомогательные расчеты приведены
в табл. 9.5
Слайд 12Средний интервал между поставками:
Среднее квадратическое отклонение интервала поставки:
Средний объем поставки:
Среднее квадратическое
отклонение объема поставки:
Слайд 13Средний интервал между требованиями:
Среднее квадратическое отклонение интервала расхода:
Средний объем требования:
Среднее квадратическое
отклонение объема требований:
Слайд 15Расчет показал, что норма текущего запаса, рассчитанная по разным формулам, колеблется
от 0,7 до 5 дн.. т. е наблюдается почти семикратное расхождение результатов расчета. это объясняется присутствием четырех случайных величин, характеризующих процессы поставки и расхода двигателей: интервала времени между поставками, объема поставки, интервала времени между требованиями и объемом требований (расхода), тогда как формулы табл. 9.1, по которым были рассчитаны нормы текущего запаса, учитывают в основном не более двух случайных величин.
Слайд 16Для определения нормы страхового запаса по формулам табл. 9.2 необходимо выполнить
вспомогательные расчеты, табл. 9.6.
Слайд 17
Таким образом, из анализа результатов расчета страхового запаса по формулам табл.
9.2 следует, что диапазон значений колеблется от 2 до 7 дн., что несколько меньше, чем размах таких значений для нормы текущего запаса
Слайд 18Пример 9.2.
Рассчитаем норму текущего и страхового запаса для циклического процесса с
ежедневным расходом и фиксированной величиной максимального запаса
= 25 ед. Статистические параметры поставки и расхода следующие:
средний интервал между поставками: =5 дн.;
среднее квадратическое отклонение интервала поставки: = 1 дн.;
средний расход: Rcp = 5ед./дн.;
среднее квадратическое отклонение расхода: = 2.54 ед./дн.
= 25 ед. Статистические параметры поставки и расхода следующие:
средний интервал между поставками: =5 дн.;
среднее квадратическое отклонение интервала поставки: = 1 дн.;
средний расход: Rcp = 5ед./дн.;
среднее квадратическое отклонение расхода: = 2.54 ед./дн.
Слайд 19На основе имеющихся данных смоделируем процесс поставки и расхода товара. При
разработке модели учитывалось следующее:
Продолжительность цикла поставки Tj подчиняется определенному закону распределения, вид которого и необходимые статистические параметры заданы. В частном случае это нормальный закон.
Ежедневный расход di подчиняется закону распределения, вид которого задается. В частном случае это нормальный закон.
Моделирование величин di продолжается до момента времени , при этом в каждом цикле проверяется условие
(9.5)
Продолжительность цикла поставки Tj подчиняется определенному закону распределения, вид которого и необходимые статистические параметры заданы. В частном случае это нормальный закон.
Ежедневный расход di подчиняется закону распределения, вид которого задается. В частном случае это нормальный закон.
Моделирование величин di продолжается до момента времени , при этом в каждом цикле проверяется условие
(9.5)
Слайд 20Если условие не соблюдается (не наблюдается дефицита), то при поступлении следующей
поставки на складе в виде запаса сохраняется случайное количество изделий . Эта случайная величина необходима для моделирования последующих циклов как начальное значение величины запаса на складе (вместе с поставкой )При раздельном моделировании циклов может быть выведена как самостоятельный результат моделирования. Если условие (9.5) соблюдается, то фиксируется как время наступления, так и количество дней дефицита.
4. Предусматривается реализация процессов, у которых начальное значение запаса отличается от Q, рассчитываемого по формуле
4. Предусматривается реализация процессов, у которых начальное значение запаса отличается от Q, рассчитываемого по формуле
Слайд 21Разница по существу, представляет собой страховой запас. Очевидно,
варьируя величину можно добиться условия, что вероятность отсутствия дефицита будет составлять заданную величину, например Р= 0.95 или P=0,99.
Таким образом, в результате моделирования формируются массивы следующих случайных величин: d - суммарный расход изделий;
-остаток на складе на момент поступления новой партии; - количество дней дефицита; -дефицит изделий. Указанные случайные величины подвергаются традиционной статистической обработке.
Таким образом, в результате моделирования формируются массивы следующих случайных величин: d - суммарный расход изделий;
-остаток на складе на момент поступления новой партии; - количество дней дефицита; -дефицит изделий. Указанные случайные величины подвергаются традиционной статистической обработке.
Слайд 22На рис. 9.1 показана графическая интерпретация результатов моделирования процесса поставки и
расхода.
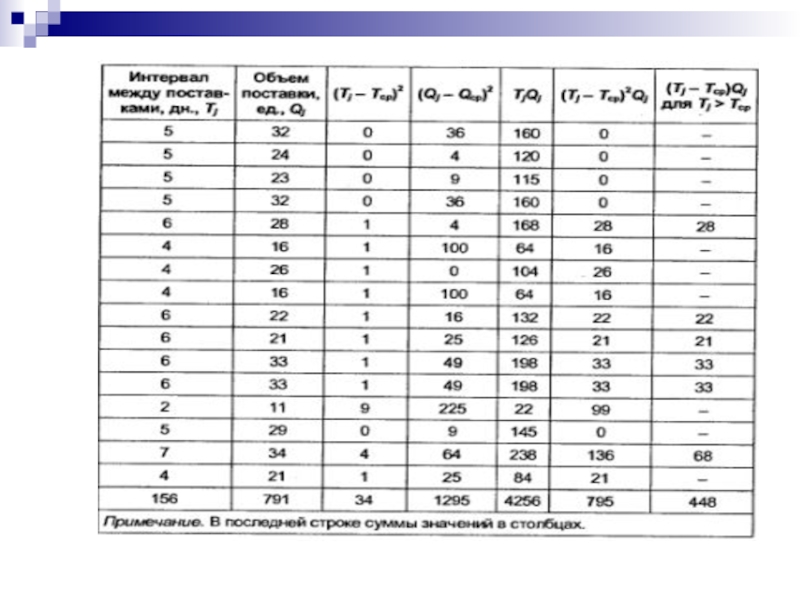
Слайд 23Результаты моделирования 30 циклов и промежуточные вычисления для расчета нормы запаса
приведены в табл. 9.7.
Слайд 25По результатам моделирования получили:
средний интервал между поставками
Среднее квадратическое отклонение интервала
поставки
средний объем поставки
Среднее квадратическое отклонение объема поставки
средний объем поставки
Среднее квадратическое отклонение объема поставки
Слайд 26Расчет нормы текущего и страхового запаса по формулам табл. 9.1 И
9.2 представлен в табл. 9.8 и 9.9
Слайд 305. Если в момент времени суммарный ежедневный расход достигает
начального запаса на складе , т. е. возникает ситуация дефицита, то предполагается, что неудовлетворенные заявки продолжают накапливаться до случайного момента времени поступления нового заказа. Таким образом, при речь идет не о реальном, а о прогнозируемом процессе накопления заявок на интервале .Случайные накопленные величины дефицита используются для оценки страхового запаса.
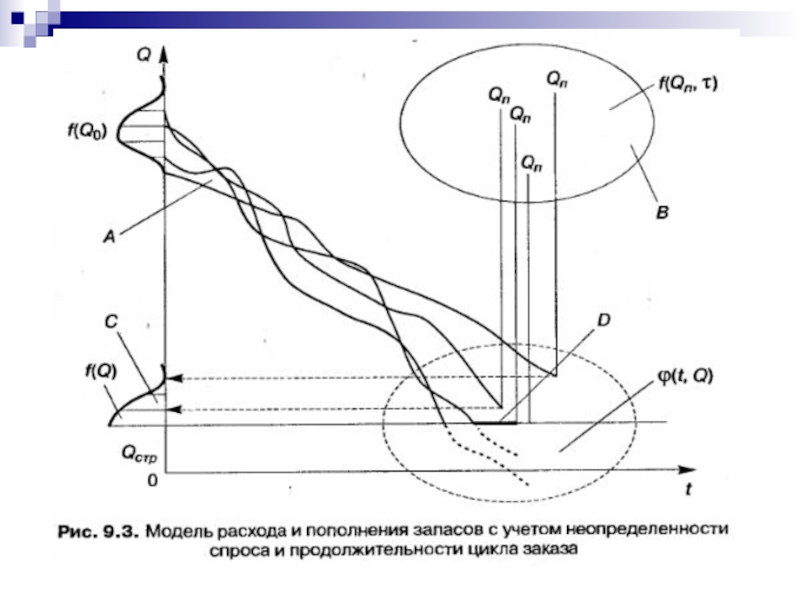
Слайд 31Для расчета величины страхового запаса в условиях неопределенности в работах рекомендована
формула
(9.6)
где k – коэффициент, определяемый с помощью табулированной функции - общее среднее квадратичное отклонение.
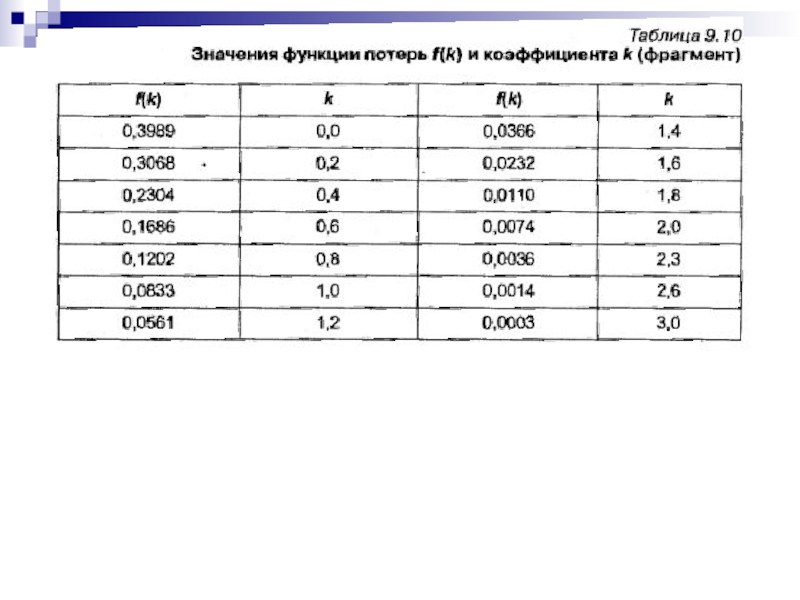
Функция - функция потерь, которая определяется площадью, ограниченной правой ветвью «кривой нормального распределения». В табл. 9.10 приведены значения
(9.6)
где k – коэффициент, определяемый с помощью табулированной функции - общее среднее квадратичное отклонение.
Функция - функция потерь, которая определяется площадью, ограниченной правой ветвью «кривой нормального распределения». В табл. 9.10 приведены значения
Слайд 33Функция рассчитывается по формуле (9.7)
Где SL –
величина дефицита; Q – размер заказа.
Входящее в формулы (9.6) и (9.7) общее среднее квадратическое отклонение рассчитывается по формуле
(9.8)
где — соответственно среднее значение продолжительности функционального цикла и количество продаж продукта в день; — соответственно средние квадратические отклонения случайных величин Т и D.
Входящее в формулы (9.6) и (9.7) общее среднее квадратическое отклонение рассчитывается по формуле
(9.8)
где — соответственно среднее значение продолжительности функционального цикла и количество продаж продукта в день; — соответственно средние квадратические отклонения случайных величин Т и D.