- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы рейтинговой (комплексной) оценки деятельности организаций в комплексном экономическом анализе презентация
Содержание
- 1. Методы рейтинговой (комплексной) оценки деятельности организаций в комплексном экономическом анализе
- 2. Рейтинговая оценка Под термином «рейтинговая оценка» понимается
- 3. Ранжирование Ранжирование – распределение экономических величин по
- 4. Такому упорядочению при экономико-математическом моделировании подвергаются, например,
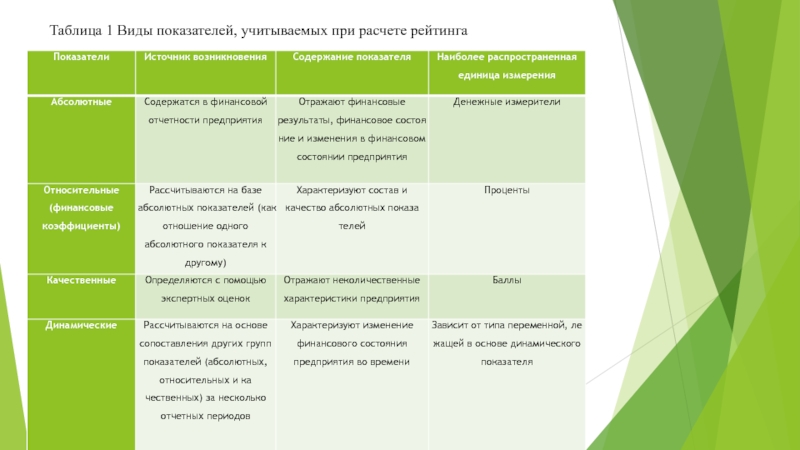
- 5. Основные виды показателей, используемых при расчете рейтинговой
- 6. Таблица 1 Виды показателей, учитываемых при расчете рейтинга
- 7. Основные методы рейтинговой оценки предприятия
- 8. Таблица 2 - Основные методы рейтинговой оценки предприятия
- 9. Упорядоченный-балансовый. Методы «эталонного предприятия» и «удачливого конкурента».
- 10. 1. Исходные данные представляются в виде матрицы A={aij}
- 11. 4. Для каждого
- 12. Таксонометрический. Он не только учитывает абсолютные значения показателей,
- 13. Метод регрессионных остатков. В основе данного метода
- 14. 1. Определяется модель зависимости результата работы как функция
- 15. 4. Метод рейтинговой экспресс-оценки финансового состояния предприятия.
- 16. 5. Метод cумм. Значение показателя комплексной оценки для
- 17. Если мы проранжируем каждый столбец матрицы А на ее
- 18. 6. Метод геометрической средней. Интегральный показатель Kj вычисляется
- 19. Так же, как и метод сумм, метод
- 20. 8. Метод суммы мест. Применение данного метода
- 21. Классификационный-балансовый. Кластерный анализ. Кластерный анализ применяется в
- 22. 2. Дискриминантный анализ. Дискриминантный анализ предполагает,
- 23. Упорядоченный-экспертный. 1. Метод суммы преимуществ. Этот метод
- 24. 2. На основе частных матриц предпочтительности каждого
- 25. 2. Метод непосредственного ранжирования альтернатив. Алгоритм данного
- 26. Классификационно-экспертный. Проведение иерархической процедуры классификации на основе
- 27. 2. Практическая часть. Метод комплексной оценки деятельности
- 28. Решение: Проранжируем предприятия и заполним табл. 4.
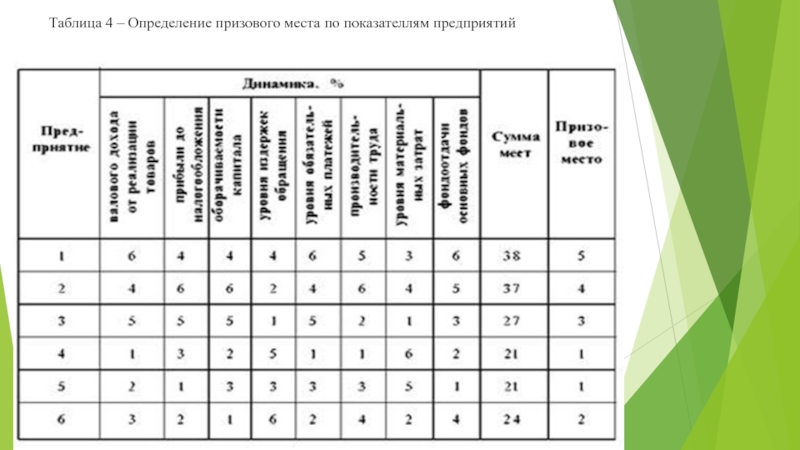
- 29. Таблица 4 – Определение призового места по показателлям предприятий
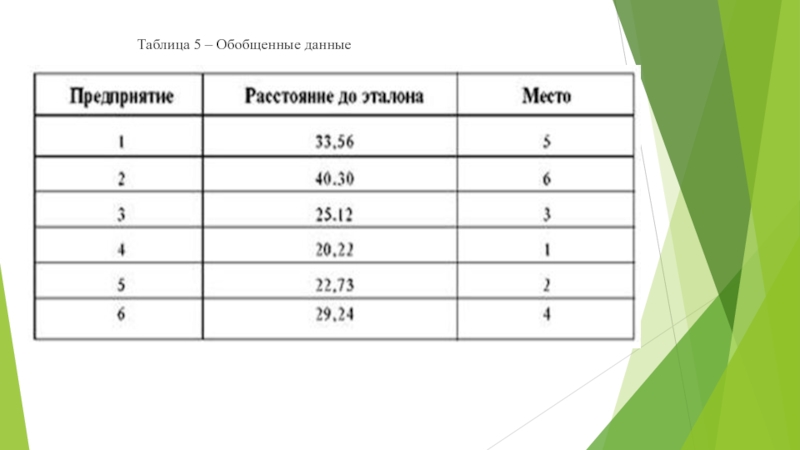
- 30. Таблица 5 – Обобщенные данные
- 31. Используя цифровые значения показателей, приведенные в табл.
- 32. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего
«Уфимский государственный нефтяной технический университет»
МЕТОДЫ РЕЙТИНГОВОЙ (КОМПЛЕКСНОЙ) ОЦЕНКИ ДЕЯТЕЛЬНОСТИ ОРГАНИЗАЦИЙ В КОМПЛЕКСНОМ ЭКОНОМИЧЕСКОМ АНАЛИЗЕ
Презентация
по дисциплине «Экономический анализ и управление производством»
Студент гр. МТП-21-16-01 Р.Р. Диваев
Руководитель канд. экон. наук, доц. О.А. Александрова
Слайд 2Рейтинговая оценка
Под термином «рейтинговая оценка» понимается место организации в классификации либо
Слайд 3Ранжирование
Ранжирование – распределение экономических величин по возрастающим или убывающим показателям, характеризующим
Слайд 4Такому упорядочению при экономико-математическом моделировании подвергаются, например, показатели качества продукции, показатели
Слайд 5Основные виды показателей, используемых при расчете рейтинговой оценки
Обычно проводится
Упорядоченный
Классификационный
Слайд 7Основные методы рейтинговой оценки предприятия
В методологическом плане выделяются
бухгалтерский (балансовый) подход
экспертный подход
Слайд 9Упорядоченный-балансовый.
Методы «эталонного предприятия» и «удачливого конкурента».
Этот метод авторы также называют «методом
Слайд 101. Исходные данные представляются в виде матрицы A={aij}
где по строкам записаны номера
2. Формируется «эталонное предприятие», в соответствии с которым и будет проводиться ранжирование. Существуют два основных способа такого выбора предприятия. Первый заключается в том, что для каждого из п выбранных показателей определяется норматив, соответствующий эталонному предприятию. Второй способ предполагает, что по каждому показателю находится максимальное или оптимальное значение по исследуемой совокупности (простроение «удачливого конкурента»). На основе выбранных значений формируется столбец условного эталонного предприятия (m + l).
3. Исходные показатели матрицы [aij] стандартизуются в отношении соответствующего показателя «эталонного предприятия» по
формуле:
где хij — стандартизированные показатели состояния у-го предприятия.
Слайд 11 4. Для каждого анализируемого предприятия значение его
по формуле
Также возможна модификация исходной формулы с учетом весовых коэффициентов:
где ki — весовые коэффициенты, определяемые исследователем
в соответствии со значимостью соответствующих показателей.
5. Предприятия ранжируются в порядке возрастания рейтинговой оценки. Наивысший рейтинг имеет предприятие с минимальным значением р (т.е. предприятие, показатели наиболее близки к выбранному эталону).
Слайд 12Таксонометрический. Он не только учитывает абсолютные значения показателей, но и позволяет элиминировать
Слайд 13Метод регрессионных остатков. В основе данного метода лежит регрессионный анализ. Базовая
Слайд 141. Определяется модель зависимости результата работы как функция от параметров деятельности и
Rj=f(a1j,a2j,…,anj)+Effj ,
где j=1,2,..., m — номер исследуемого предприятия;
R — показатель, характеризующий результат работы предприятия;
Eff— показатель эффективности.
2. В соответствии с выбранными параметрами и показателем результата деятельности предприятий строят регрессию по выбор- ке, получая формулу, на основе которой рассчитывается средний результат деятельности каждого предприятия Rf
3. Далее для каждого предприятия вычисляются регрессионные остатки Eff = (Rj, - R), которые и являются показателем его эффективности.
4. Совокупность упорядочивается по убыванию показателя Eff.
Слайд 154. Метод рейтинговой экспресс-оценки финансового состояния предприятия. Идея, на которой основан
1. Устанавливаются нормативные значения показателей Ni,i=1,2,…,m. Отметим, что способов выбора нормативных значений показателей аналогичен способу выбора «эталонного предприятия»: они могут быть установлены исследователем независимо от анализируемой совокупности либо отобраны как наилучшие по выборке значения.
2. На основе имеющихся данных вычисляются показатели Ki, учитываемые при расчете рейтинговой оценки.
3. Определяется рейтинговое число:
На данном этапе также возможен подбор весовых коэффициентов, определяющих значимость каждого показателя.
4.Совокупность упорядочивается по убыванию рейтингового числа.
Слайд 165. Метод cумм. Значение показателя комплексной оценки для каждого предприятия (Пi) рассчитывается
где Рj — весовой коэффициент для j-го исходного показателя.
Чем выше результаты работы предприятия, тем больше значение показателя комплексной оценки.
В современной литературе часто используется понятие предприятия-эталона, с которым сопоставляются все объекты анализа. Некоторые авторы предлагают использовать в качестве такого эталона абстрактное предприятие, у которого все показатели имеют наилучшее значение среди данной совокупности. Практически такой условный эталон строится на основе матрицы А как строка, элементы которой определяются по формуле
a0j = max (aij), i = 1,2,3,…,m, j = 1,2,3,…,n.
Слайд 17Если мы проранжируем каждый столбец матрицы А на ее максимальный элемент, т.е. на
Пi = Pj a’ij , где a’ij = a’ij/ a0j
Данные показатеи разумеется, не могут быть больше, чем показатели эталона. Хотя коэффициенты П'j будут близки к определенным выше коэффициентам Пj, распределение мест среди предприятий может несколько измениться, особенно это относится к предприятиям с близкими значениями комплексных показателей.
Основной недостаток метода сумм — уравнивание частных оценок, что требует введения дополнительных весовых коэффициентов при них, определение числовых значений которых представляет самостоятельную сложную проблему
Слайд 186. Метод геометрической средней.
Интегральный показатель Kj вычисляется как средняя геометрическая коэффициентов роста
Условия применения совпадают с условиями применения метода сумм. Выводы делаются аналогичным образом.
7. Метод коэффициентов.
Интегральный показатель Kj рассчитывается как произведение коэффициентов роста показателей
Слайд 19Так же, как и метод сумм, метод коэффициентов применим только для однонаправленных
Слайд 208. Метод суммы мест.
Применение данного метода предполагает предварительное ранжирование хозяйствующих субъектов
где ij - место, которое занимает j-й хозяйствующий субъект по i-му показателю.
Если ввести весовые коэффициенты (коэффициенты значимости показателей), интегральный показатель будет рассчитываться по формуле
где αi - коэффициент значимости i-го показателя.
В отличие от ранее рассмотренных методов, метод суммы мест может применяться и для однонаправленных, и для разнонаправленных показателей. Кроме того, могут использоваться как абсолютные, так и относительные значения показатели (темпы роста).
Слайд 21Классификационный-балансовый.
Кластерный анализ.
Кластерный анализ применяется в том случае, когда исследователь не располагает
- число классов априори задано;
- число классов неизвестно.
Основной идеей, на которой строится кластерный анализ, является определение взаимного расположения (степени близости) объектов в n-мерном пространстве признаков. Результатом реализации кластер-процедуры является разделение исследуемой совокупности на заранее известное либо определяемое в ходе анализа, число однородных классов. [7]
Слайд 222. Дискриминантный анализ.
Дискриминантный анализ предполагает, что исследователю известны обучаюшие выборки.
Слайд 23Упорядоченный-экспертный.
1. Метод суммы преимуществ. Этот метод является одной из простейших модификаций
1. Каждый из l экспертов производит последовательное сравнение пар альтернатив и указывает, какая из альтернатив наиболее предпочтительна. На основе этих сравнений для каждого эксперта строится матрица предпочтительности:
A={aij(k)},
где k – 1,2,…., l – номер эксперта;
aij(k) – результат парного сравнения k-м экспертом i-го и j-го объектов, причем:
aij(k)=1, если объект i предпочтительнее объекта j;
aij(k)=0,5, если оба объекта в равной степени предпочтительны;
aij(k)=0, если объект I менее предпочтителен, чем объект j;
Слайд 242. На основе частных матриц предпочтительности каждого эксперта формируется итоговая матрица:
3.
4. Итоговое упорядочение совокупности происходит по убыванию суммы рангов. 4. Итоговое упорядочение совокупности происходит по убыванию суммы рангов.
Слайд 252. Метод непосредственного ранжирования альтернатив. Алгоритм данного метода заключается в следующем.
1.
2. Итоговый рейтинг объекта выставляется по итоговой сумме всех элементов строки:
При этом возможно применение весовых коэффициентов для каждого столбца, характеризующих существенность ранжировки по данному признаку или учитывающих квалификацию эксперта. Совокупность упорядочивается по убыванию рейтингового числа.
Слайд 26Классификационно-экспертный.
Проведение иерархической процедуры классификации на основе экспертного подхода.
По своему содержанию близко
1. На первоначальном этапе каждый объект представляет собой один однородный класс. Эксперту предлагается найти в исследуемой совокупности два наиболее схожих класса, которые объединяются в один.
2. Процедура повторяется до тех пор, пока все объекты не окажутся в одном классе. Далее эксперту предлагается определить, на каком из шагов процедуры сформировалась устойчивая структура.
3. В соответствии с этим выбирается оптимальное число классов и входящие в каждый из них объекты. [8]
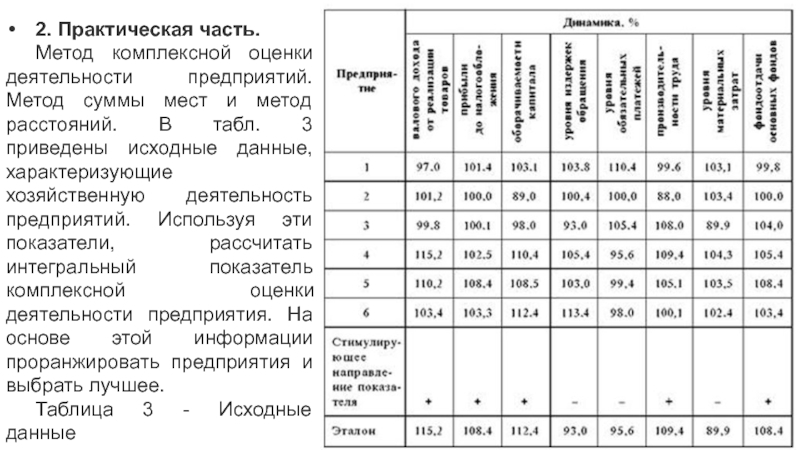
Слайд 272. Практическая часть.
Метод комплексной оценки деятельности предприятий. Метод суммы мест и
Таблица 3 - Исходные данные
Слайд 28Решение:
Проранжируем предприятия и заполним табл. 4. Например, по объему валового дохода
Первое место поделили предприятия 4 и 5, которые набрали равное количество баллов (по 21 баллу), второе место заняло предприятие 6 (24 балла) и т. д.
Слайд 31Используя цифровые значения показателей, приведенные в табл. 5, решим задачу методом
Аналогично рассчитаем расстояние до эталона для остальных пяти предприятий и заполним табл. 5.
Вывод. Наименьшее отклонение показателей предприятий от эталона имеет предприятие 4, которое по праву заняло первое место.