- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Методы и методики среднесрочного прогнозирования социально-экономических процессов презентация
Содержание
- 1. Методы и методики среднесрочного прогнозирования социально-экономических процессов
- 2. Высшая школа экономики, Санкт-Петербург Классификация социально-экономических процессов
- 3. Высшая школа экономики, Санкт-Петербург Базовые определения фото
- 4. Высшая школа экономики, Санкт-Петербург Методы прогнозирования в
- 5. Мы рассмотрим прогнозирование только стационарных процессов
- 6. Нормальный закон распределения вероятностей случайной величины Обратимые
- 7. Нормальный закон распределения вероятностей случайной величины
- 8. Средняя арифметическая и её свойства В числе
- 9. Прогноз случайной стационарной величины Если есть основания
- 10. Пример Средняя арифметическая цены 0,5 литра ряженки
- 11. Чаще всего приходится иметь дело с нормально
- 12. Как выявить причинно-следственную связь? Взаимосвязь между двумя
- 13. Как выявить причинно-следственную связь? Наиболее часто в
- 14. Типовые прогнозные модели Самый простой случай для
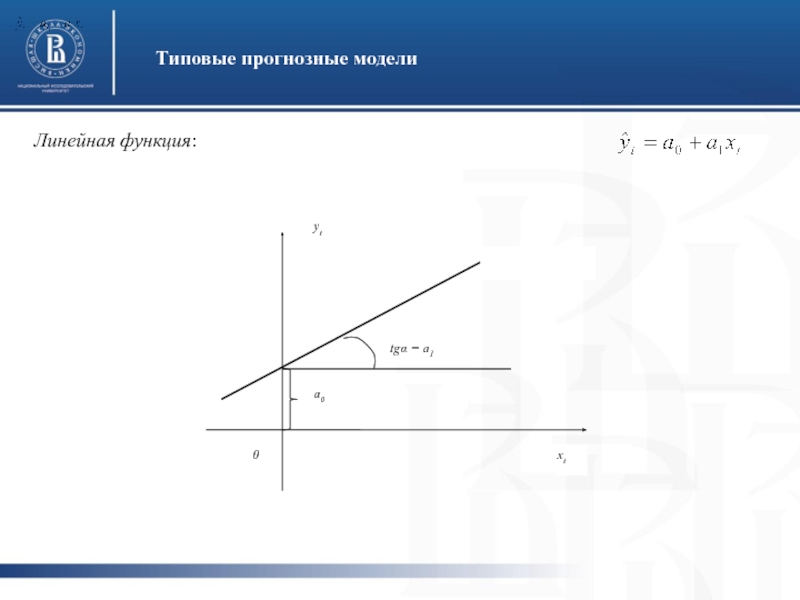
- 15. Типовые прогнозные модели Линейная функция:
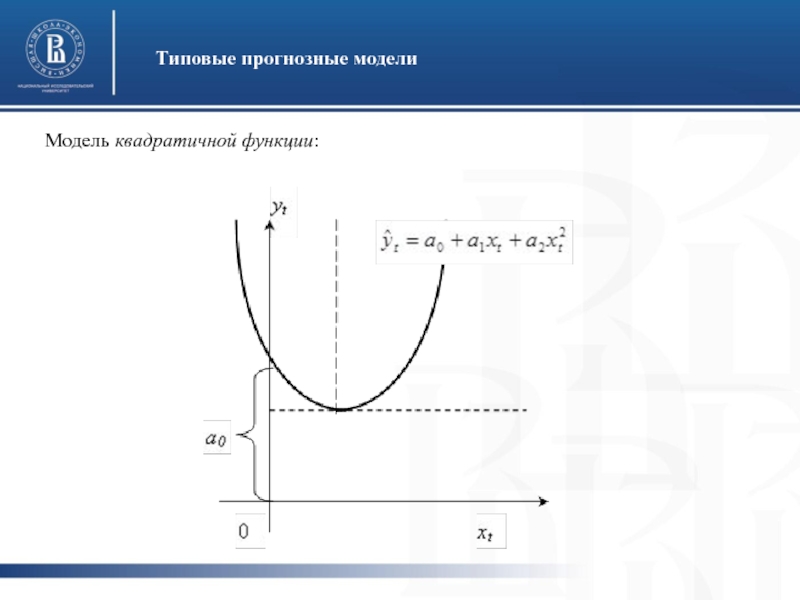
- 16. Типовые прогнозные модели Модель квадратичной функции:
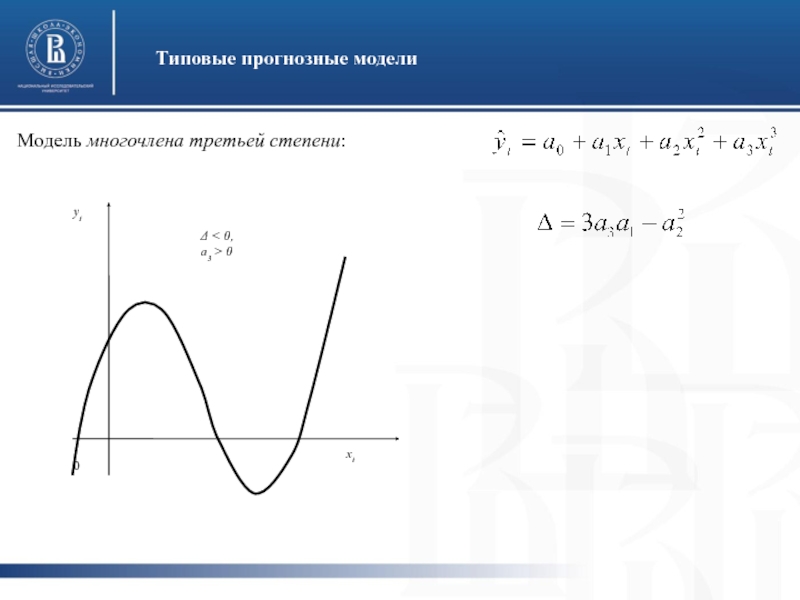
- 17. Типовые прогнозные модели Модель многочлена третьей
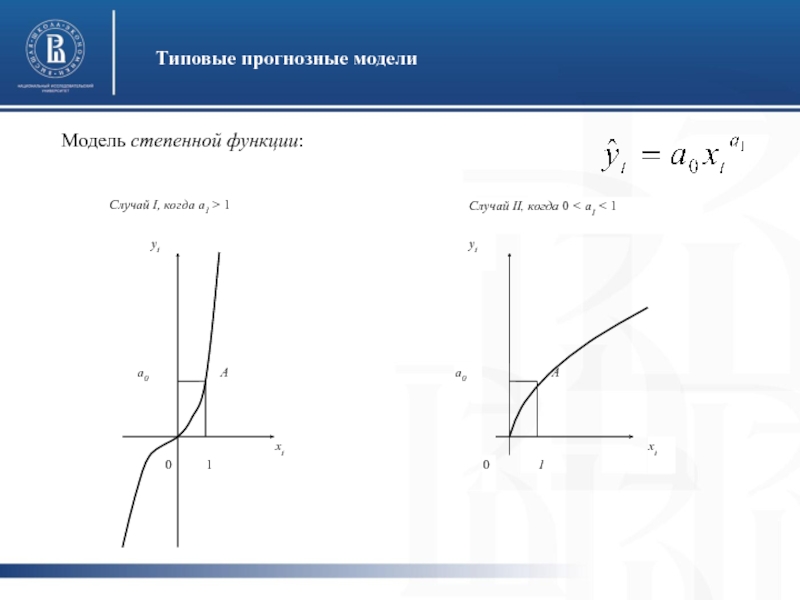
- 18. Типовые прогнозные модели Модель степенной функции:
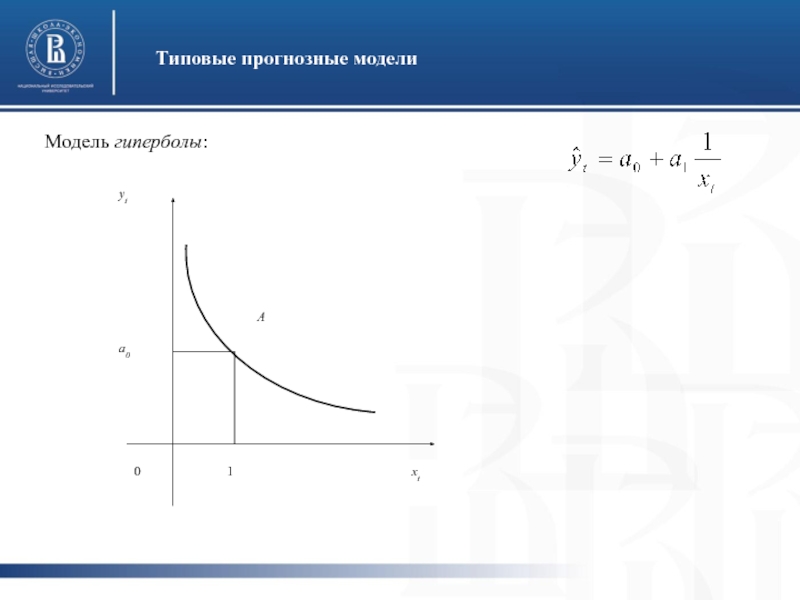
- 19. Типовые прогнозные модели Модель гиперболы:
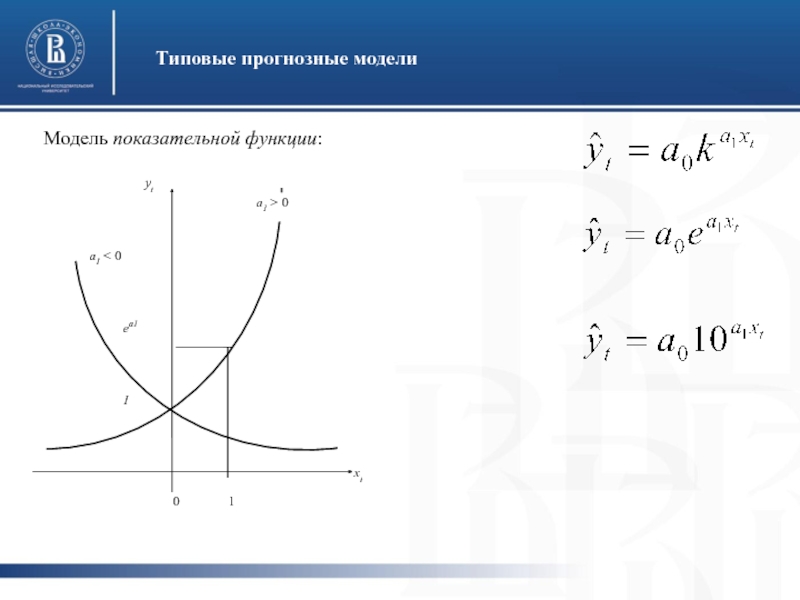
- 20. Типовые прогнозные модели Модель показательной функции:
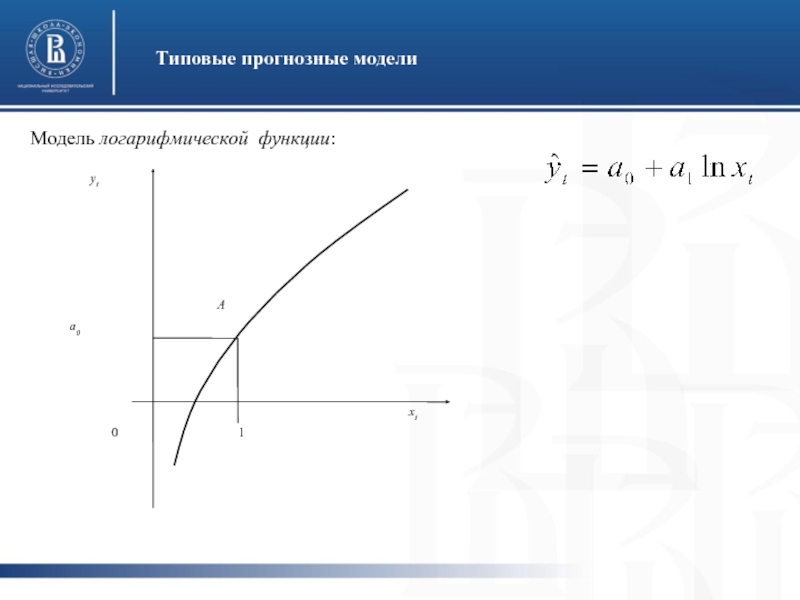
- 21. Типовые прогнозные модели Модель логарифмической функции:
- 22. Метод наименьших квадратов Рассмотрим вначале простую линейную
- 23. Метод наименьших квадратов Метод
- 24. Метод наименьших квадратов, для квадратичной функции (и любой аддитивной функции) использовать легко:
- 25. Нелинейные модели Для мультипликативных моделей непосредственное использование
- 26. Нелинейные модели В таком случае используют приём
- 27. Как выполнить прогноз? После вычисления с помощью
- 28. Метод наименьших квадратов для многофакторных моделей
- 29. Метод наименьших квадратов
- 30. Мультиколлинеарность Мультиколлинеарность, как следует из самого названия,
- 31. Вывод: Любые прогнозы не носят точечный характер. Они всегда – интервальны!
Слайд 1Методы и методики среднесрочного прогнозирования социально-экономических процессов
Автор
Проф. С.Г.Светуньков
Высшая школа экономики
www.hse.ru
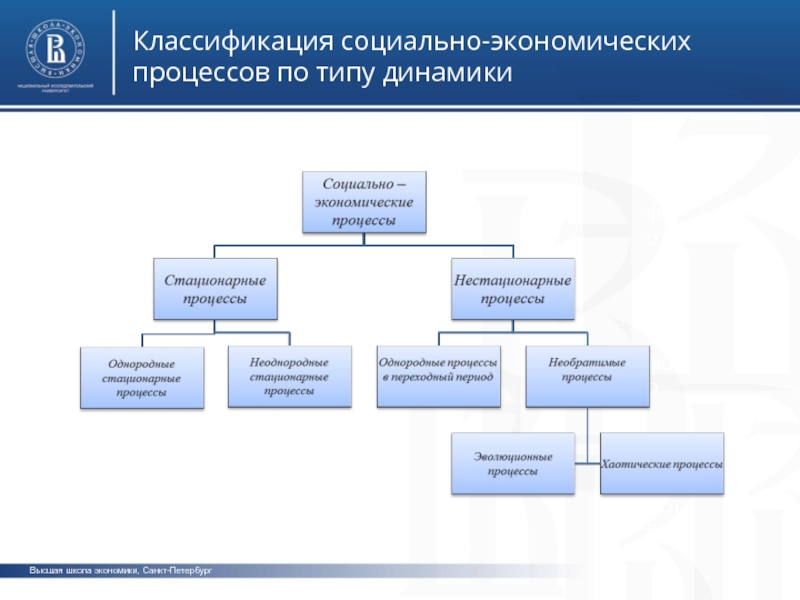
Слайд 2Высшая школа экономики, Санкт-Петербург
Классификация социально-экономических процессов по типу динамики
фото
фото
фото
Слайд 3Высшая школа экономики, Санкт-Петербург
Базовые определения
фото
фото
фото
Под стационарными рядами понимаются ряды случайных процессов,
при любом фиксированном действительном τ.
Под нестационарными в промежуток времени от t до t + T обратимыми процессами понимаются такие из них, характеристики которых меняются вариантно относительно временных сдвигов:
где приращение ∆y(t+τ) не определяется характеристиками процессов в предыдущие моменты времени.
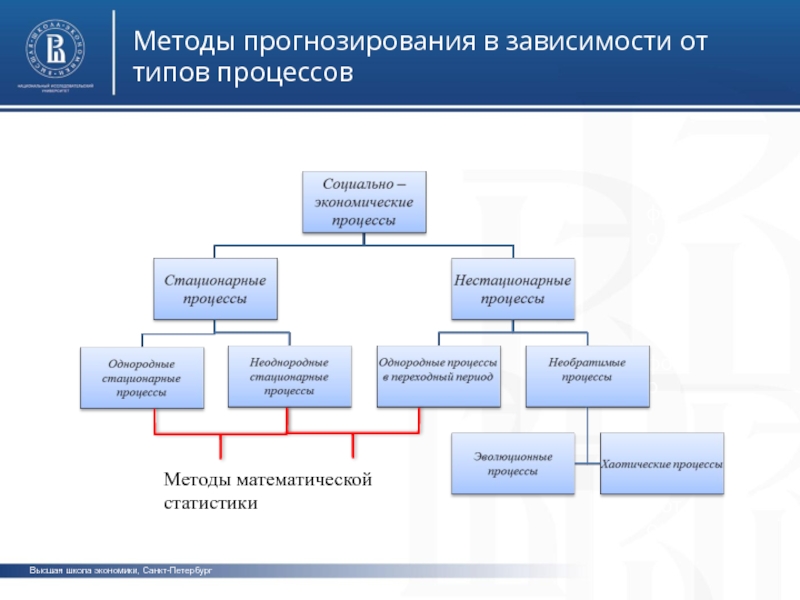
Слайд 4Высшая школа экономики, Санкт-Петербург
Методы прогнозирования в зависимости от типов процессов
фото
фото
фото
Методы математической
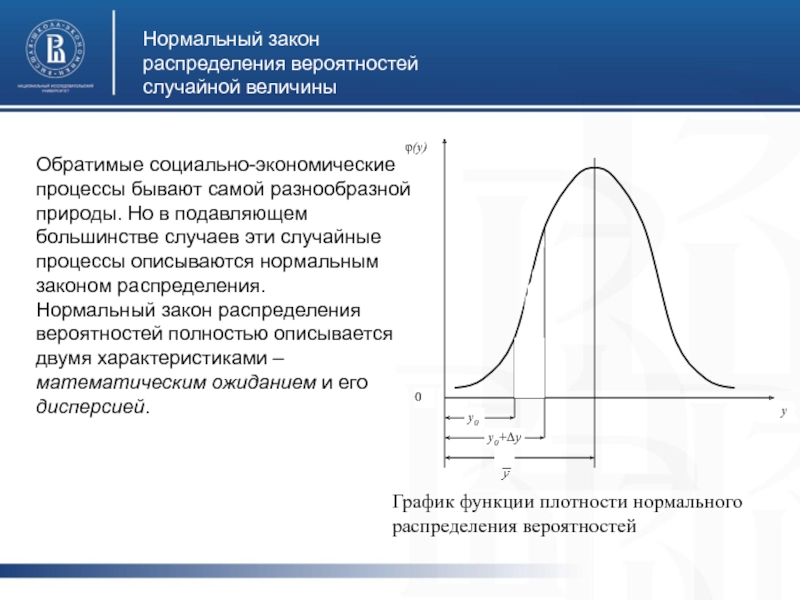
Слайд 6Нормальный закон распределения вероятностей случайной величины
Обратимые социально-экономические процессы бывают самой разнообразной
Нормальный закон распределения вероятностей полностью описывается двумя характеристиками – математическим ожиданием и его дисперсией.
График функции плотности нормального распределения вероятностей
Слайд 7Нормальный закон распределения вероятностей случайной величины
Гаусс предложил функцию, аппроксимирующую нормальный
Здесь μy - математическое ожидание случайной величины y,
σy - дисперсия этой случайной величины.
Откуда взялась эта функция? Просто Гаусс сначала изучил более простую функцию, а именно:
А потом искал ответ на вопрос: где бы её применить? А тут как раз попалась статистическая задача…
Слайд 8Средняя арифметическая и её свойства
В числе средних величин, используемых в прогнозировании,
Средняя арифметическая представляет собой частное от деления суммы значений показателя на число элементов выборочной совокупности:
Важной характеристикой генеральной совокупности является дисперсия дискретной случайной величины, которая представляет собой сумму квадратов отклонения каждого значения случайной величины от её математического ожидания, умноженную на вероятность этого значения.
Для работы не с генеральной совокупностью, а с выборкой из неё используют такую формулу:
Слайд 9Прогноз случайной стационарной величины
Если есть основания считать, что случайная величина распределена
Прогнозируемая величина будет лежать в пределах:
m – число степеней свободы (число независимых наблюдений минус число оцениваемых статистических параметров)
Слайд 10Пример
Средняя арифметическая цены 0,5 литра ряженки по данным 126 магазинов Выборгского
Выборочное значение дисперсии оказалось равным :
Число степеней свободы – m=126-1. Значение t-статистики Стьюдента для 125 степеней свободы при уровне значимости 0,05 равно 1,9791.
Значит, с доверительной вероятностью в 95% прогнозная величина цены пол литра ряженки в магазине «О’кей» у метро «Озерки» будет лежать в пределах:
Слайд 11Чаще всего приходится иметь дело с нормально распределёнными случайными процессами
Это означает,
Находим модель, описывающую математическое ожидание процесса,
Вычисляем выборочное значение дисперсии,
Выполняем прогноз,
Оцениваем прогнозные границы.
Но поскольку данные обратимые процессы протекают в условиях неоднородности, возникает задача выявления и формального описания связки: причины во внешнем окружении → следствия в прогнозируемом процессе.
Это и есть искомая прогнозная модель.
Слайд 12Как выявить причинно-следственную связь?
Взаимосвязь между двумя случайными факторами называется «корреляционной».
Если мы
На первом этапе необходимо провести профессиональный анализ возможных взаимосвязей и обосновать наличие и возможную форму взаимосвязи.
На втором этапе необходимо использовать инструменты корреляционного анализа.
Слайд 13Как выявить причинно-следственную связь?
Наиболее часто в корреляционном анализе используется коэффициент парной
Поэтому этот коэффициент свидетельствует только о том, насколько предполагаемая связь между двумя факторами приближается к линейной.
Он не помогает выявить взаимосвязь, а свидетельствует о возможности её описания линейной зависимостью.
Слайд 14Типовые прогнозные модели
Самый простой случай для прогнозирования, — когда число изменяющихся
Поскольку характер изменения рядов социально-экономических показателей является многообразным, то и, описывающие его модели могут иметь самые различные формы. Чаще всего в практике социально-экономического прогнозирования в качестве моделей однофакторных зависимостей используют несколько элементарных функций. Рассмотрим их.
Слайд 22Метод наименьших квадратов
Рассмотрим вначале простую линейную модель:
Она описывает исходные значения показателя
Слайд 23Метод наименьших квадратов
Метод наименьших квадратов предусматривает нахождение таких коэффициентов модели, для
В простом случае коэффициенты линейной однофакторной модели
с помощью МНК определяются просто. Надо взять первые производные функции по каждому из коэффициентов и приравнять их нулю:
Слайд 24Метод наименьших квадратов, для квадратичной функции (и любой аддитивной функции) использовать
Слайд 25Нелинейные модели
Для мультипликативных моделей непосредственное использование МНК ведёт к необходимости решения
Для него получим такую систему уравнений МНК:
Слайд 26Нелинейные модели
В таком случае используют приём линеаризации модели:
Для линеаризованной модели
Слайд 27Как выполнить прогноз?
После вычисления с помощью МНК (или какого-нибудь другого метода)
После этого определяют значение факторной переменной xt в момент прогноза τ.
Подставляя это значение в модель, получим прогноз:
Поскольку у исходных данных была некоторая дисперсия (колеблемость), то и прогноз должен быть интервальным. Для определения прогнозного интервала используют формулу оценки доверительных границ:
Слайд 28Метод наименьших квадратов для многофакторных моделей
Многофакторные модели могут быть как линейными,
Метод наименьших квадратов для данной аддитивной функции использовать легко:
Слайд 30Мультиколлинеарность
Мультиколлинеарность, как следует из самого названия, возникает тогда, когда факторы модели
В этой ситуации оценки коэффициентов многофакторных моделей с помощью МНК будут очень неточными и неустойчивыми - они меняют свои значения и часто знаки даже при изменении порядка округления.
Так как оценки параметров оказываются неточными, то интерпретация влияния факторов на прогнозируемый показатель будет совершенно не той, которая есть на самом деле.
Ценность таких моделей крайне низка, так как неустойчивая модель даёт очень сильную вариацию своих коэффициентов, а значит и расчётных значений прогнозируемого показателя.
Модель, с помощью которой сделана попытка описать сложное многофакторное явление, не описывает это явление.