- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Индивидуальный спрос потребителя презентация
Содержание
- 1. Индивидуальный спрос потребителя
- 2. Свойства функций индивидуального спроса Анализ сравнительной статики
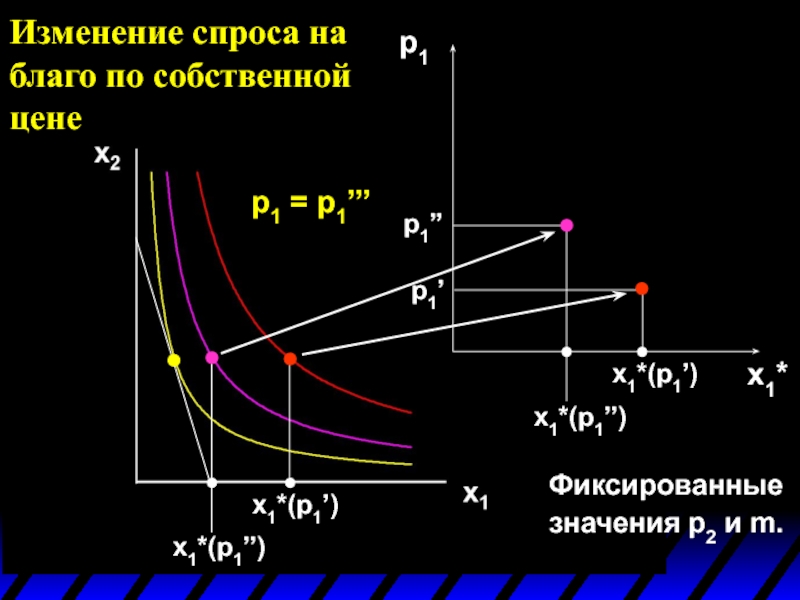
- 3. Изменение спроса на благо по собственной цене
- 4. x1 x2 p1 = p1’
- 5. Изменение спроса на благо по собственной цене
- 6. Изменение спроса на благо по собственной цене
- 7. p1 = p1’ Изменение спроса на благо
- 8. x1*(p1’) Изменение спроса на благо
- 9. x1*(p1’) p1 x1*(p1’) p1’
- 10. x1*(p1’) p1 x1*(p1’) p1’
- 11. x1*(p1’) x1*(p1’’) p1
- 12. x1*(p1’) x1*(p1’’) p1
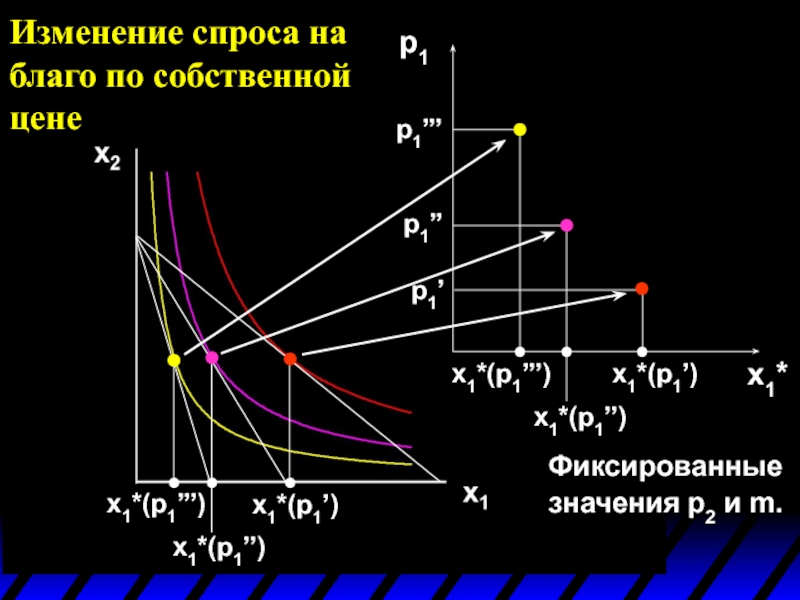
- 13. x1*(p1’) x1*(p1’’)
- 14. x1*(p1’’’) x1*(p1’) x1*(p1’’)
- 15. x1*(p1’’’) x1*(p1’) x1*(p1’’)
- 16. x1*(p1’’’) x1*(p1’) x1*(p1’’)
- 17. x1*(p1’’’) x1*(p1’) x1*(p1’’)
- 18. x1*(p1’’’) x1*(p1’) x1*(p1’’)
- 19. Изменение спроса на благо по собственной цене
- 20. Изменение спроса на благо по собственной цене
- 21. Изменение спроса на благо по собственной цене
- 22. Изменение спроса на благо по собственной цене
- 23. Изменение спроса на благо по собственной цене
- 24. Изменение спроса на благо по собственной цене
- 25. x1*(p1’’’) x1*(p1’) x1*(p1’’) Изменение
- 26. x1*(p1’’’) x1*(p1’) x1*(p1’’) p1
- 27. Изменение спроса на благо по собственной цене
- 28. Изменение спроса на благо по собственной цене
- 29. Изменение спроса на благо по собственной цене
- 30. Изменение спроса на благо по собственной цене
- 31. Изменение спроса на благо по собственной цене
- 32. Изменение спроса на благо по собственной цене
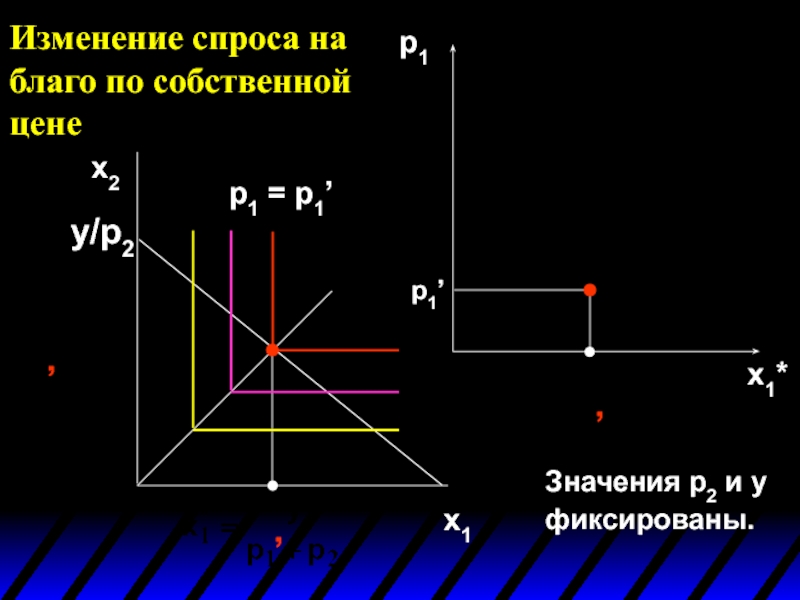
- 33. Значения p2 и y фиксированы. Изменение спроса на благо по собственной цене x1 x2
- 34. p1 x1* Значения p2 и y фиксированы.
- 35. p1 x1* Значения p2 и y фиксированы.
- 36. p1 x1* Значения p2 и y фиксированы.
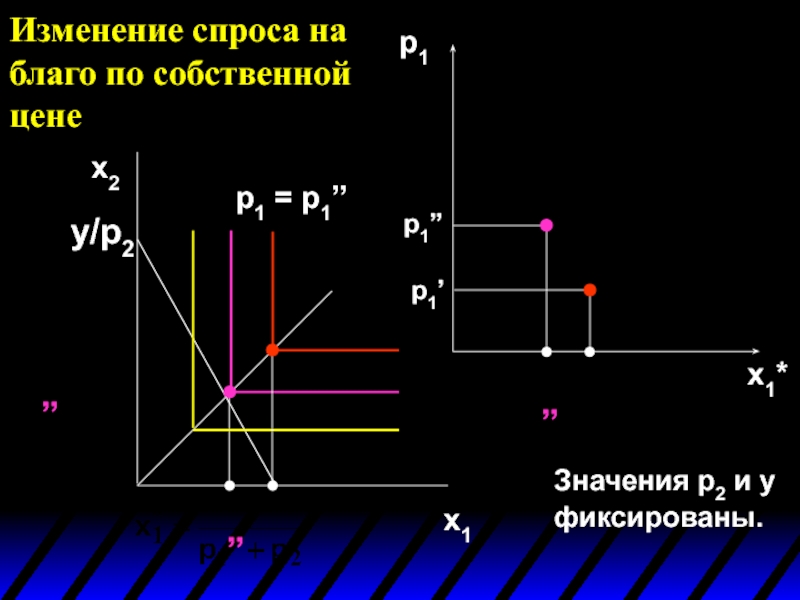
- 37. p1 x1* Кривая спроса на благо 1
- 38. Изменение спроса на благо по собственной цене
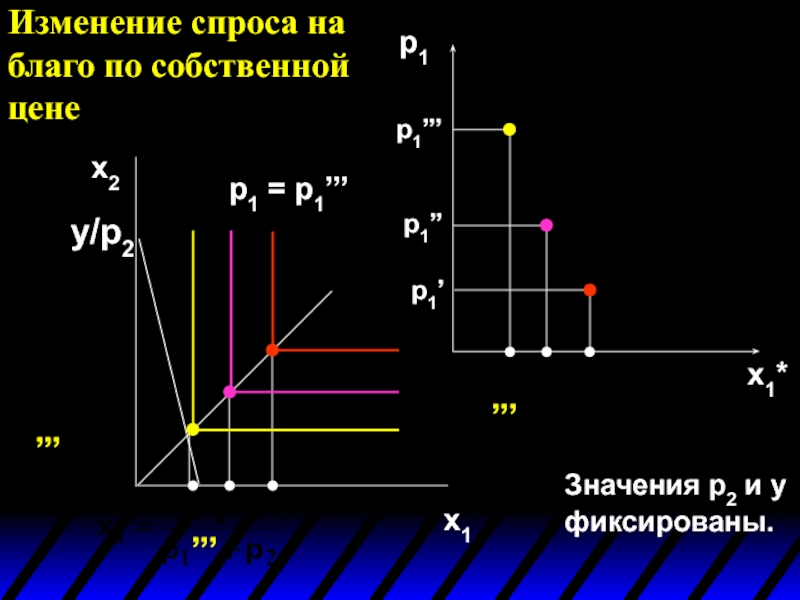
- 39. Изменение спроса на благо по собственной цене и
- 40. Изменение спроса на благо по собственной цене
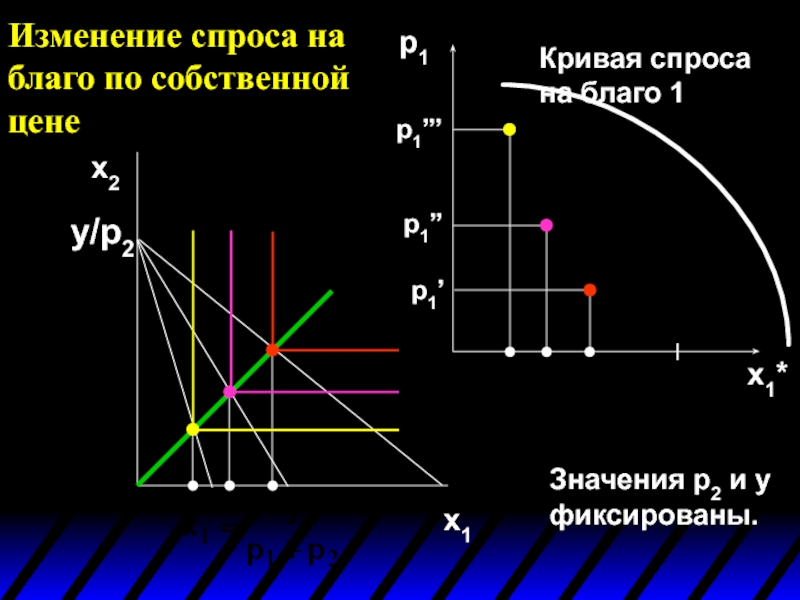
- 41. Изменение спроса на благо по собственной цене
- 42. Изменение спроса на благо по собственной цене
- 43. Изменение спроса на благо по собственной цене
- 44. Значения p2 и y фиксированы. Изменение
- 45. Изменение спроса на благо по собственной цене
- 46. Изменение спроса на благо по собственной цене
- 47. Изменение спроса на благо по собственной цене
- 48. Изменение спроса на благо по собственной цене
- 49. Изменение спроса на благо по собственной цене
- 50. Изменение спроса на благо по собственной цене
- 51. Изменение спроса на благо по собственной цене
- 52. Изменение спроса на благо по собственной цене
- 53. Изменение спроса на благо по собственной цене
- 54. Изменение спроса на благо по собственной цене
- 55. Изменение спроса на благо по собственной цене
- 56. Изменение спроса по доходу Каким образом скажется
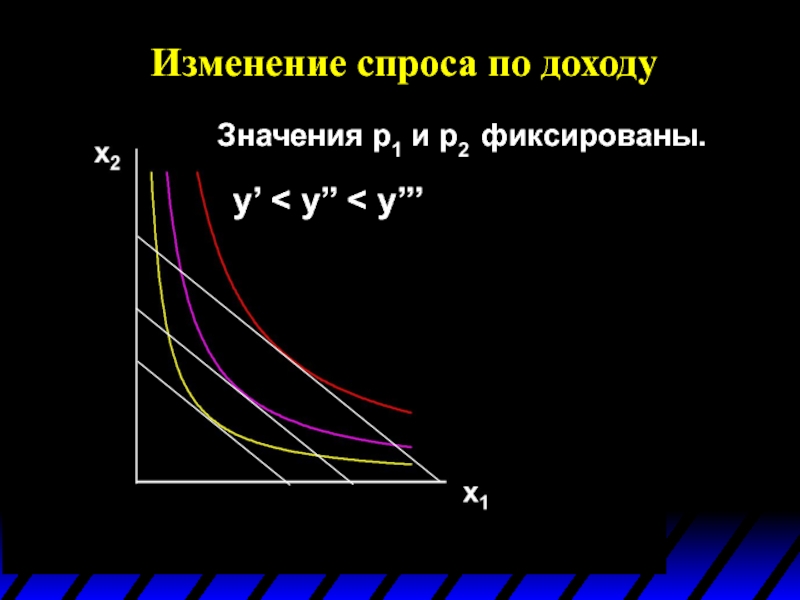
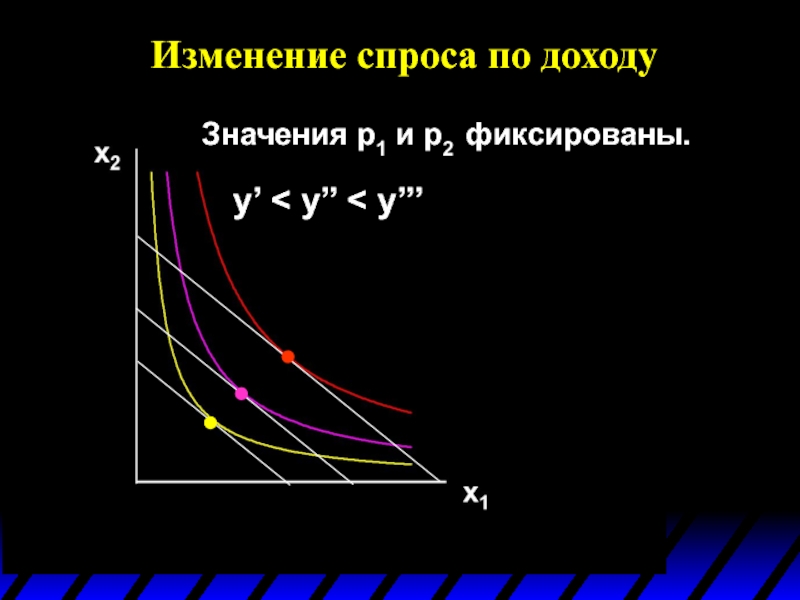
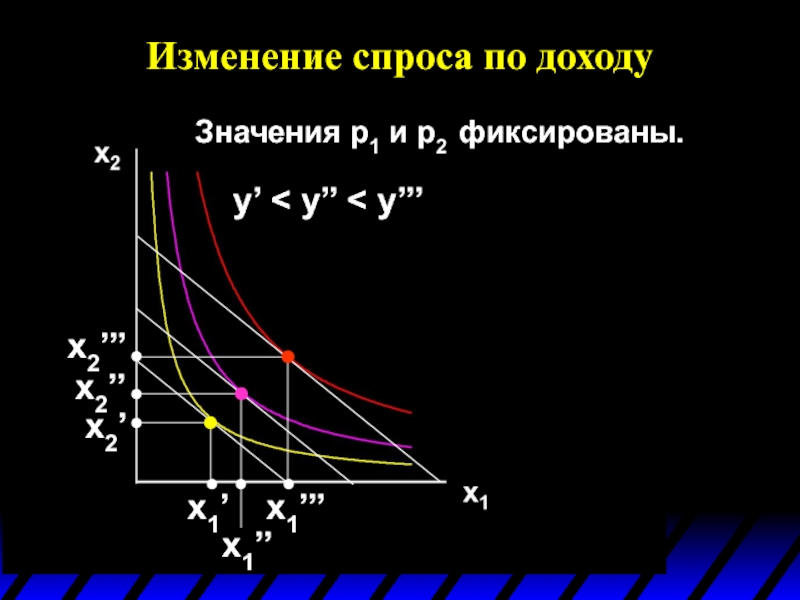
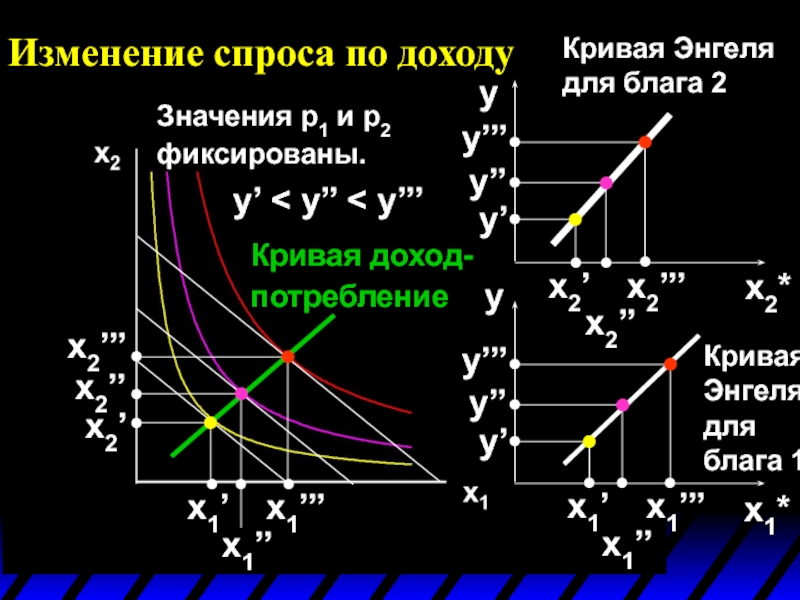
- 57. Изменение спроса по доходу Значения p1 и p2 фиксированы. y’ < y’’ < y’’’
- 58. Изменение спроса по доходу Значения p1 и
- 59. Изменение спроса по доходу Значения p1 и
- 60. Изменение спроса по доходу Значения p1 и
- 61. Изменение спроса по доходу График зависимости между
- 62. Изменение спроса по доходу Значения p1 и
- 63. Изменение спроса по доходу Значения p1 и
- 64. Изменение спроса по доходу Значения p1 и
- 65. Изменение спроса по доходу Значения p1 и
- 66. Изменение спроса по доходу Значения p1 и
- 67. Изменение спроса по доходу Значения p1 и
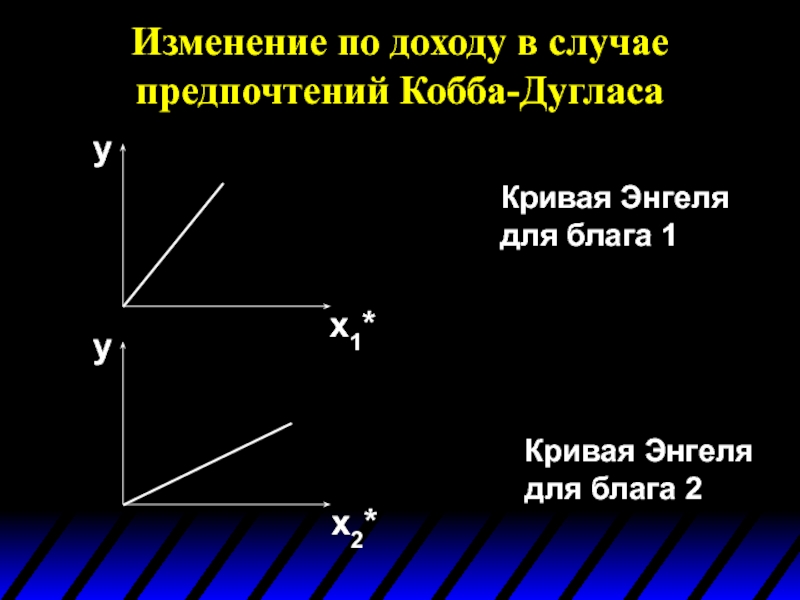
- 68. Изменение по доходу в случае предпочтений Кобба-Дугласа
- 69. Изменение по доходу в случае предпочтений Кобба-Дугласа
- 70. Изменение по доходу в случае предпочтений Кобба-Дугласа
- 71. Изменение спроса по доходу в случае взаимодополняемых
- 72. Изменение спроса по доходу в случае взаимодополняемых
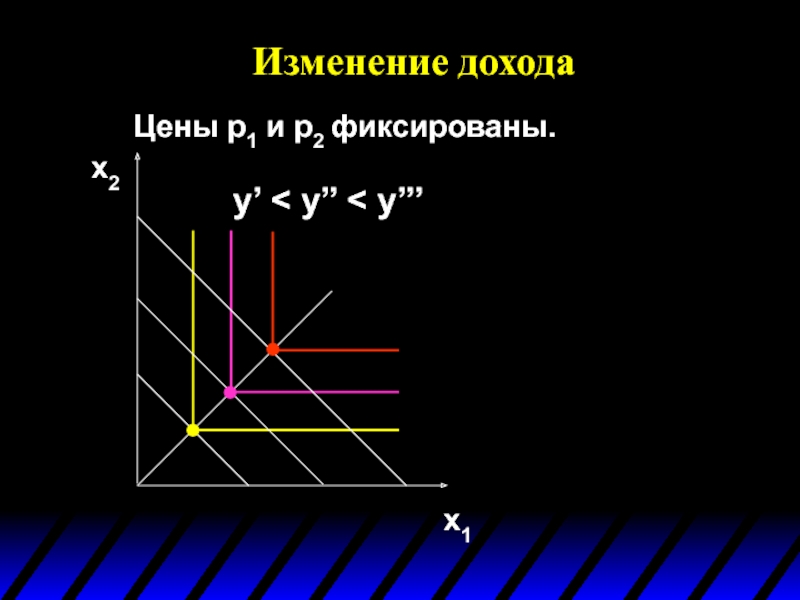
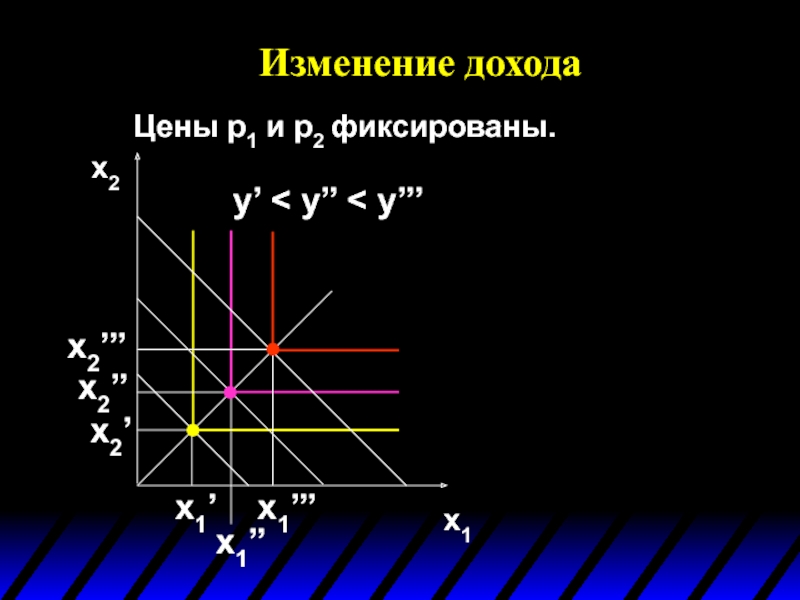
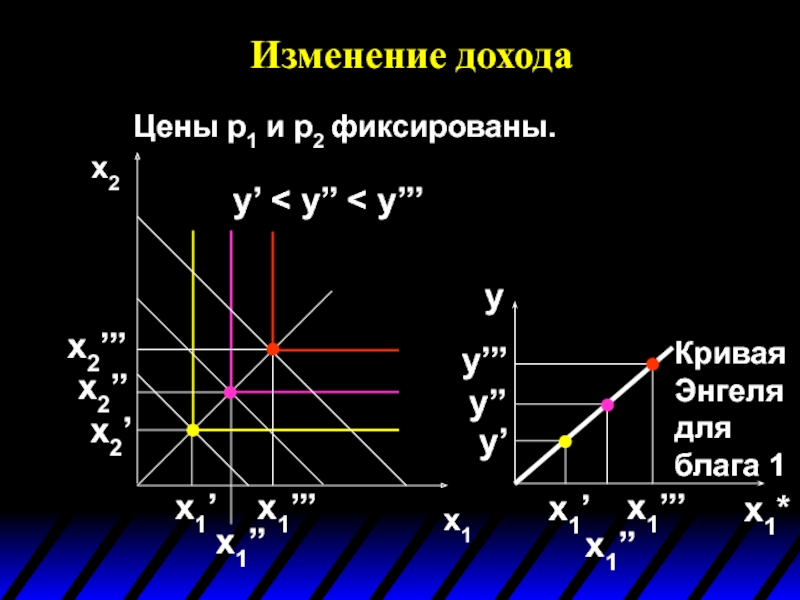
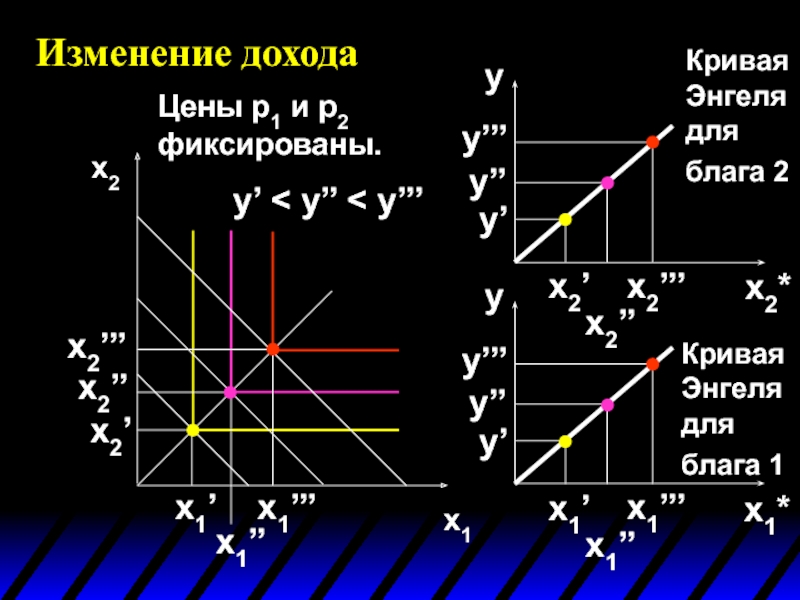
- 73. Цены p1 и p2 фиксированы. Изменение дохода x1 x2
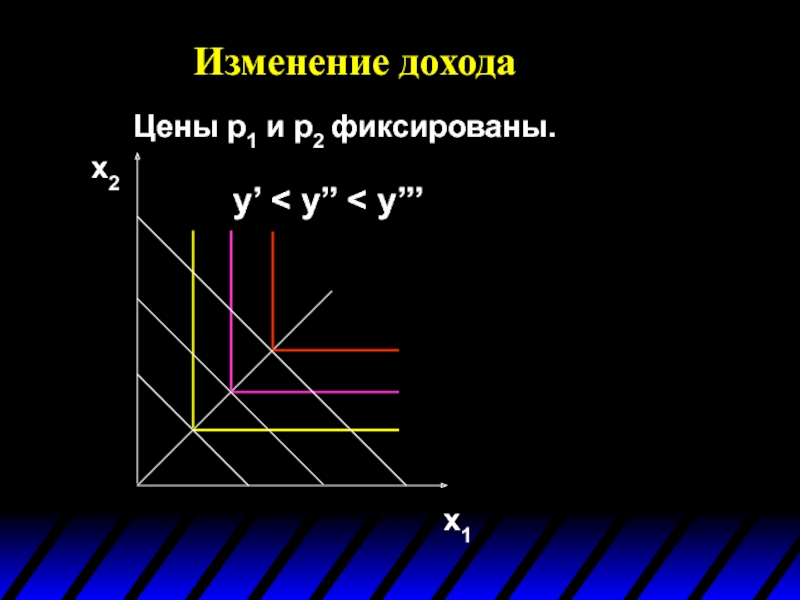
- 74. Изменение дохода x1 x2 y’ < y’’ < y’’’ Цены p1 и p2 фиксированы.
- 75. Изменение дохода x1 x2 y’ < y’’
- 76. Изменение дохода x1 x2 y’ < y’’
- 77. Изменение дохода x1 x2 y’ < y’’
- 78. Изменение дохода x1 x2 y’ < y’’
- 79. Изменение дохода x1 x2 y’ < y’’
- 80. Изменение дохода x1* x2* y y x2’’’
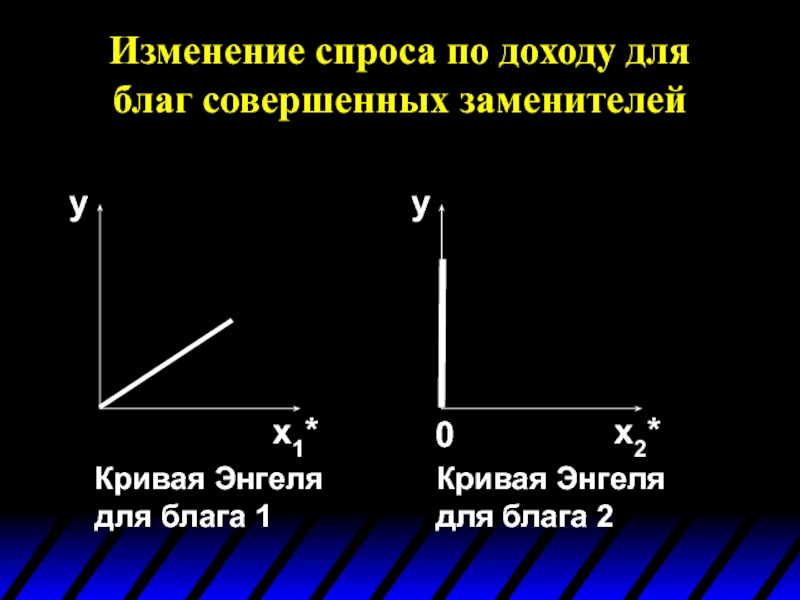
- 81. Изменение спроса по доходу для благ совершенных
- 82. Изменение спроса по доходу для благ совершенных заменителей
- 83. Изменение спроса по доходу для благ совершенных
- 84. Изменение спроса по доходу для благ совершенных заменителей Пусть p1 < p2. Тогда и
- 85. Изменение спроса по доходу для благ совершенных
- 86. Изменение спроса по доходу для благ совершенных
- 87. Изменение спроса по доходу В рассмотренных выше
- 88. Гомотетичное отношение предпочтения Отношение предпочтения называется
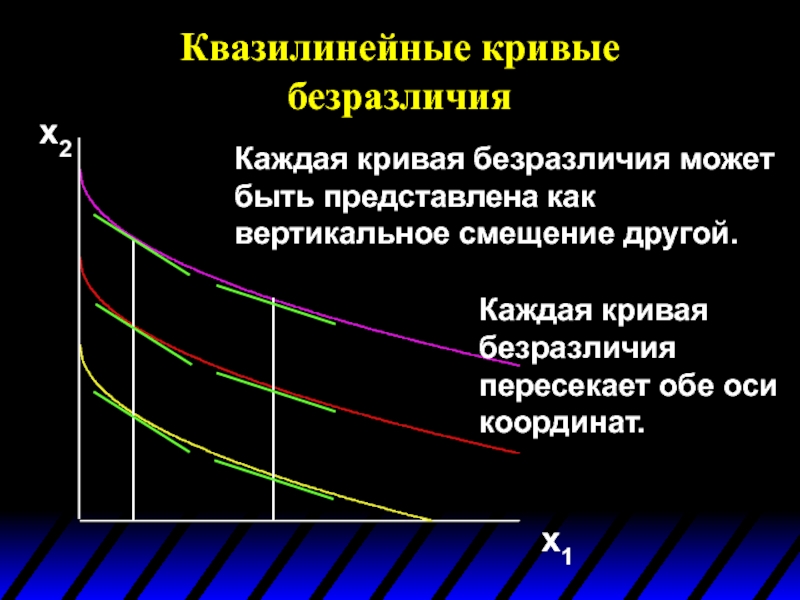
- 89. Эффекты дохода - пример негомотетичного предпочтения Квазилинейные
- 90. Квазилинейные кривые безразличия x2 x1 Каждая кривая
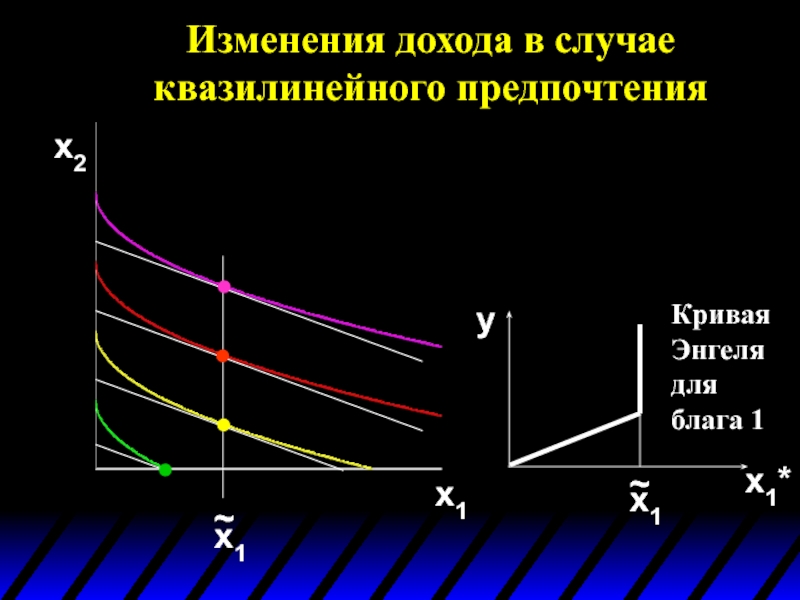
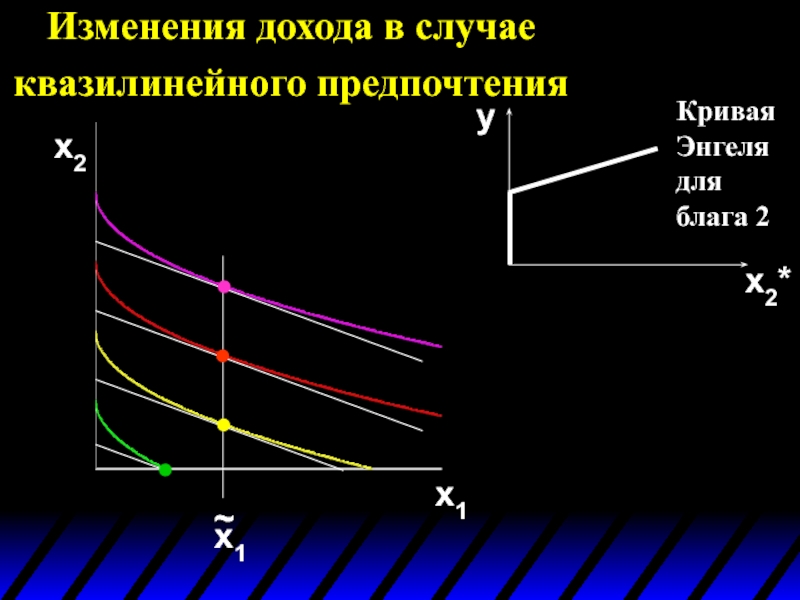
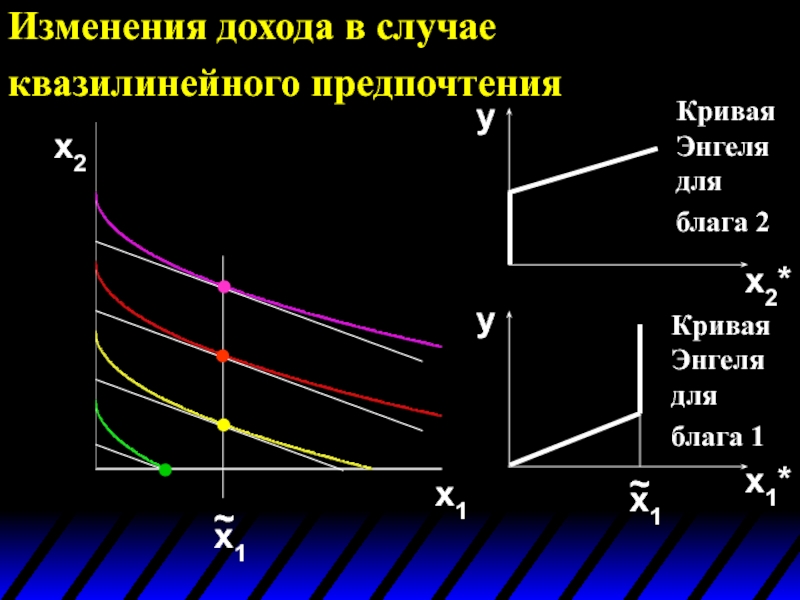
- 91. Изменения дохода в случае квазилинейного предпочтения x2 x1
- 92. Изменения дохода в
- 93. Изменения дохода в
- 94. Изменения дохода в
- 95. Характеристики изменения спроса Изменения спроса в соответствии
- 96. Гомотетичные предпочтения: функциональное представление Функция f:Rn+R называется
- 97. Гомотетичные предпочтения: функциональное представление Функция f:RnR называется
- 98. Характеристики изменения спроса Обозначим через xi*(pi) функцию,
- 99. Характеристики изменения спроса При изменении цены товара
- 100. Характеристики изменения спроса Аналогично, при изменении дохода
- 101. Эффект дохода Если для блага (товара) i
- 102. Эффект дохода Благо, спрос на которое падает с ростом дохода потребителя, т.е. xi*/ y
- 103. Изменение дохода: блага 1 и 2 нормальные
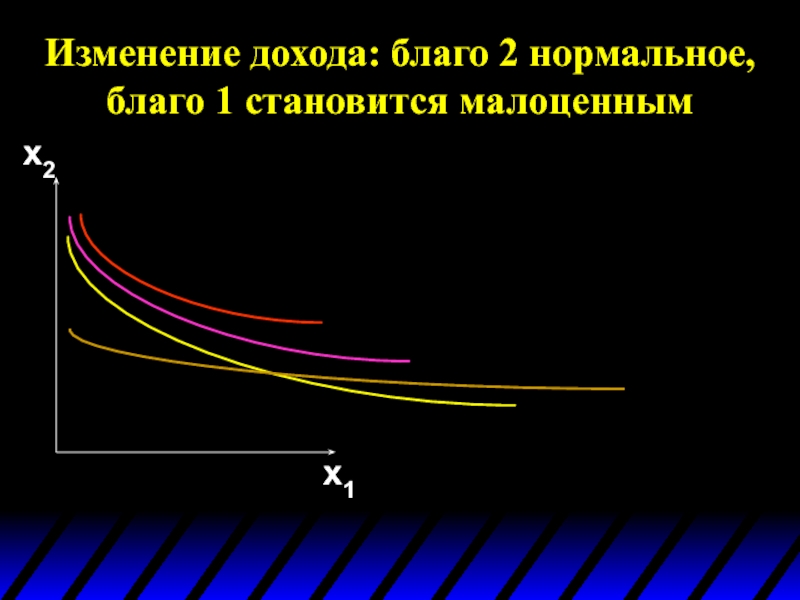
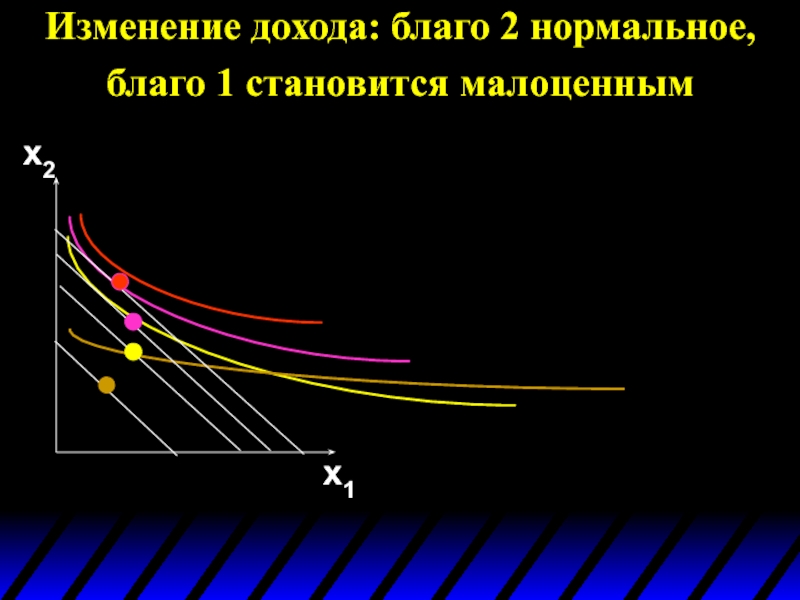
- 104. Изменение дохода: благо 2 нормальное, благо 1 становится малоценным x2 x1
- 105. Изменение дохода: благо 2 нормальное, благо 1
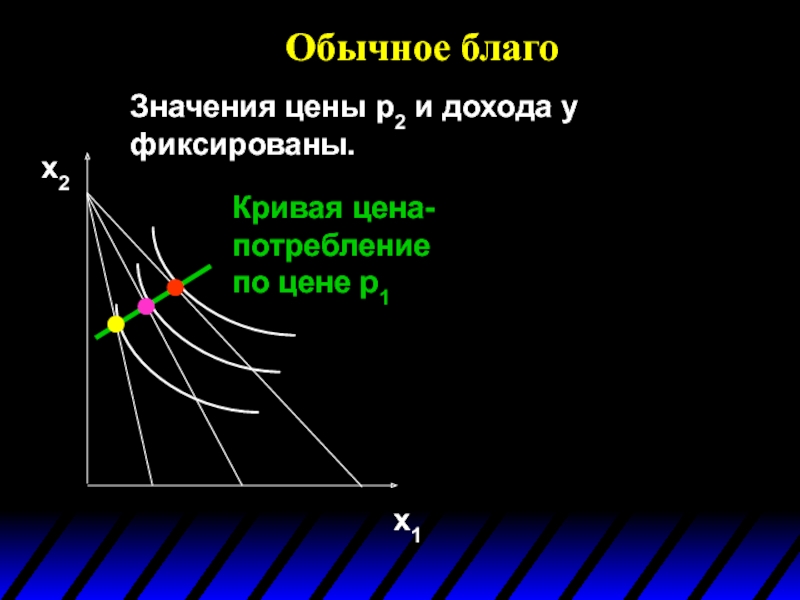
- 106. Обычное благо Благо (товар) i называется обычным,
- 107. Обычное благо Значения цены p2 и дохода
- 108. Обычное благо Значения цены p2 и
- 109. Гиффиновы блага (Giffen Goods) Если при некоторых
- 110. Oбычное благо Значения цены p2 и дохода y фиксированы. x1 x2
- 111. Oбычное благо Значения цены p2 и
- 112. Oбычное благо Значения цены p2
- 113. Перекрестные ценовые эффекты (Cross-Price Effects) В общем
- 114. Перекрестные ценовые эффекты Случай совершенных взаимодополнящих благ:
- 115. Перекрестные ценовые эффекты p1 x1* p1’
- 116. Перекрестные ценовые эффекты p1 x1* p1’
- 117. Перекрестные ценовые эффекты В случае функции полезности Кобба-Дугласа: откуда следует, что
- 118. Перекрестные ценовые эффекты В случае функции
- 119. Кривые Торнквиста Рассматривается кривая, которая описывает изменение
- 120. Кривые Торнквиста Особенности спроса на предметы (товары)
- 121. Кривые Торнквиста Товары первой необходимости Функция спроса
- 122. Кривые Торнквиста Особенности спроса на предметы длительного
- 123. Кривые Торнквиста Предметы длительного пользования Функция
- 124. Кривые Торнквиста Особенности спроса на предметы роскоши
- 125. Кривые Торнквиста Предметы длительного пользования Функция
- 126. Кривые Торнквиста a2 a1 M2 M3 x1(y) x2(y) x3(y) доход спрос
Слайд 2Свойства функций
индивидуального спроса
Анализ сравнительной статики функций индивидуального спроса - исследование характера
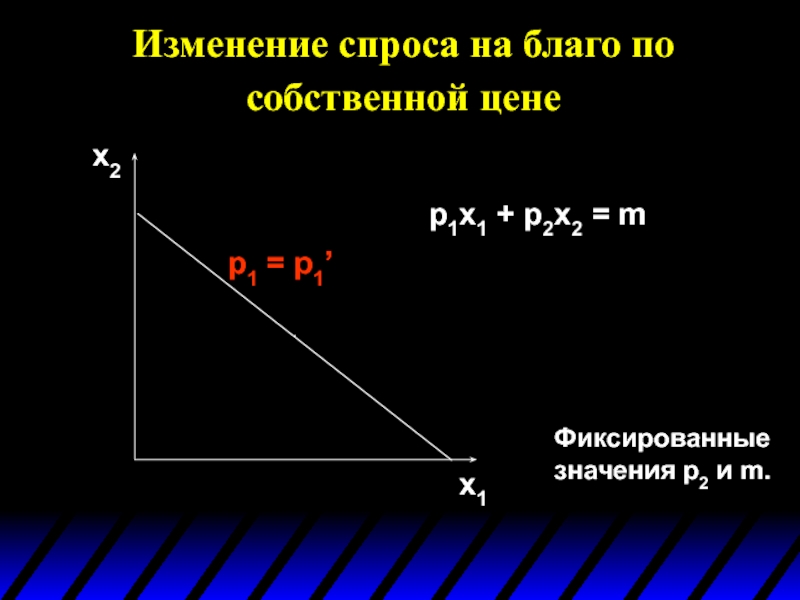
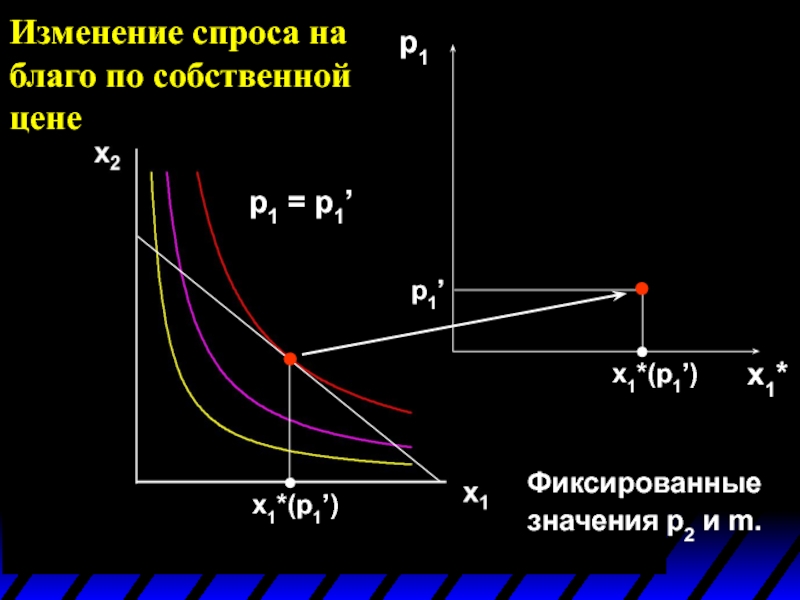
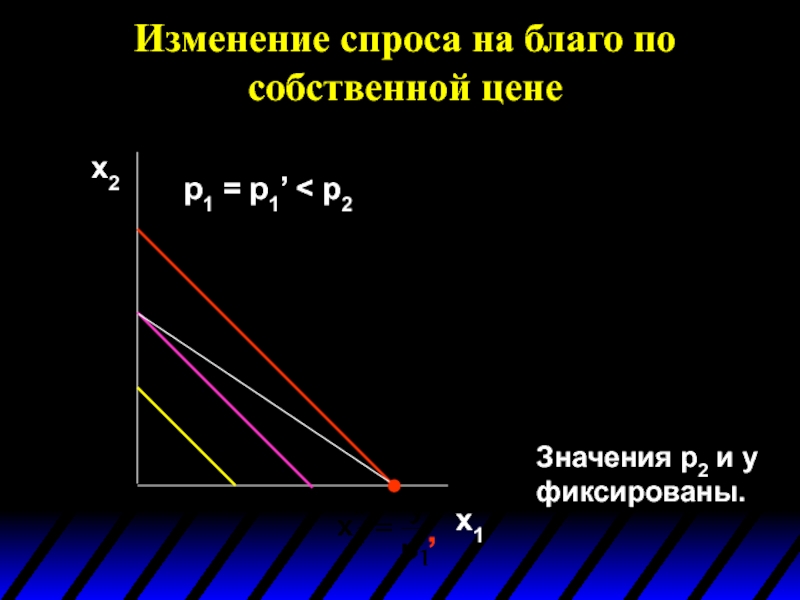
Слайд 3Изменение спроса на благо по собственной цене
Каким образом изменяется x1*(p1,p2,m) при
Предположим, что возрастает цена только первого блага p1: сначала с p1’ до p1’’, а затем с p1’’ до p1’’’.
Слайд 4
x1
x2
p1 = p1’
Фиксированные значения p2 и m.
p1x1 + p2x2 =
Изменение спроса на благо по собственной цене
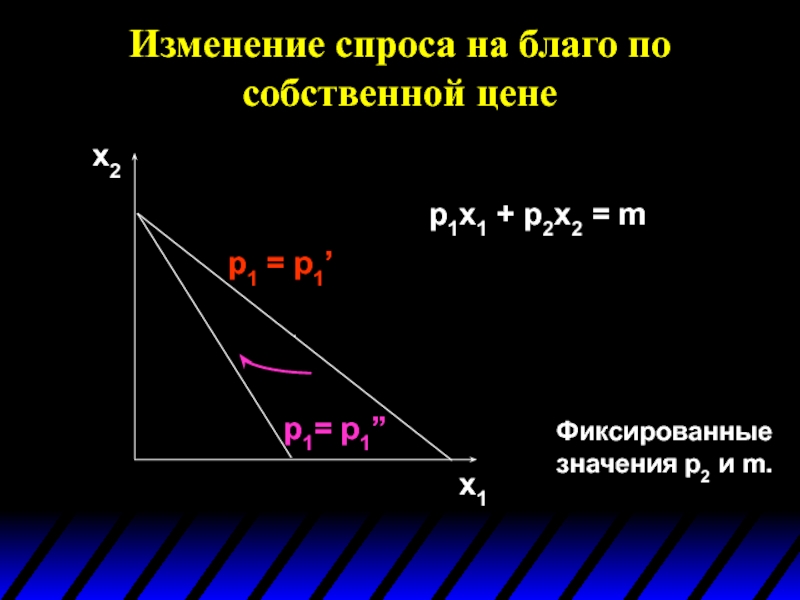
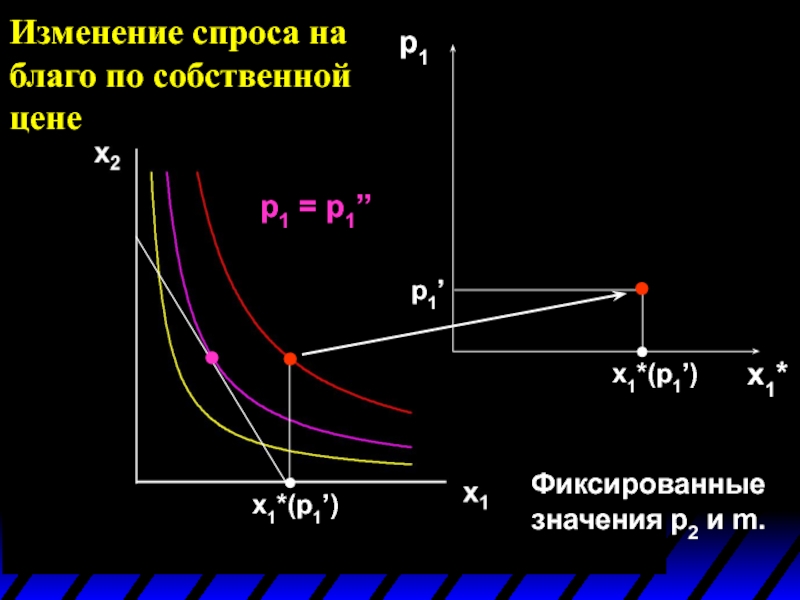
Слайд 5Изменение спроса на благо по собственной цене
x1
x2
p1= p1’’
p1 = p1’
Фиксированные значения
p1x1 + p2x2 = m
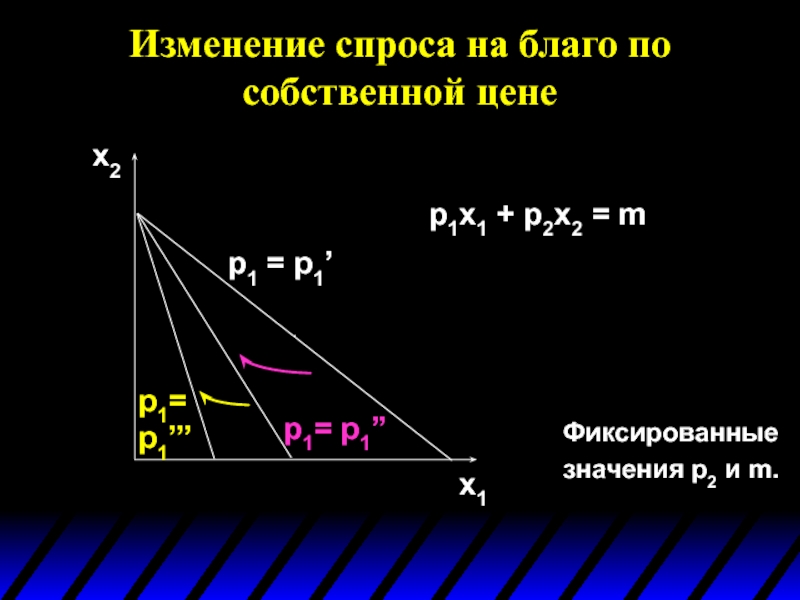
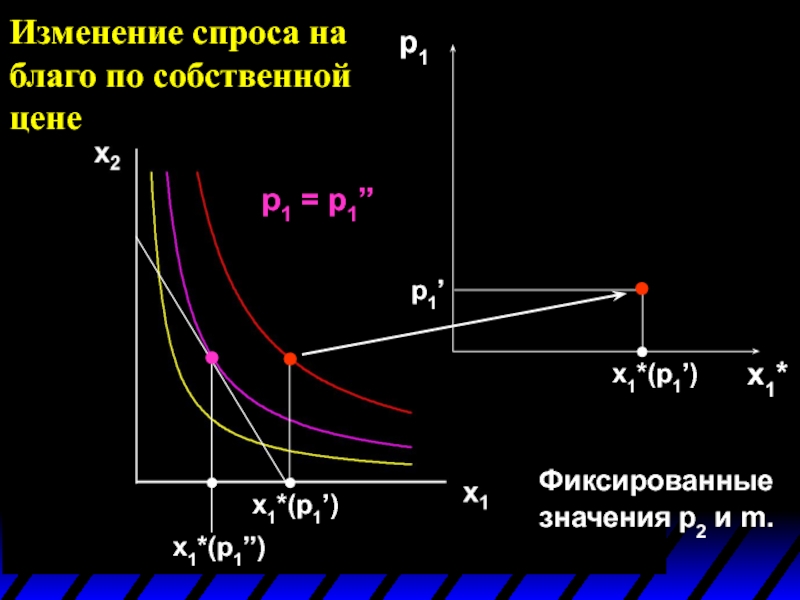
Слайд 6Изменение спроса на благо по собственной цене
x1
x2
p1= p1’’
p1=
p1’’’
Фиксированные значения p2 и
p1 = p1’
p1x1 + p2x2 = m
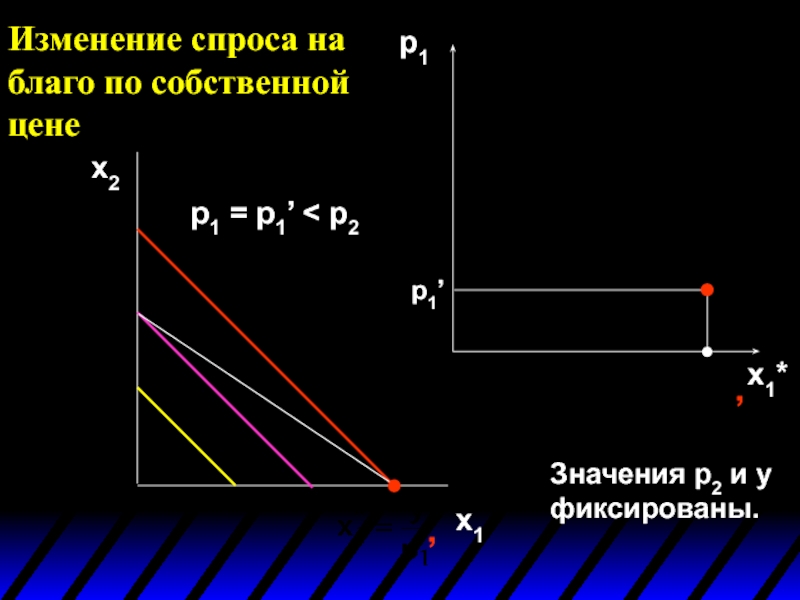
Слайд 9x1*(p1’)
p1
x1*(p1’)
p1’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2 и m.
p1 = p1’
Слайд 10
x1*(p1’)
p1
x1*(p1’)
p1’
p1 = p1’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2
Слайд 11
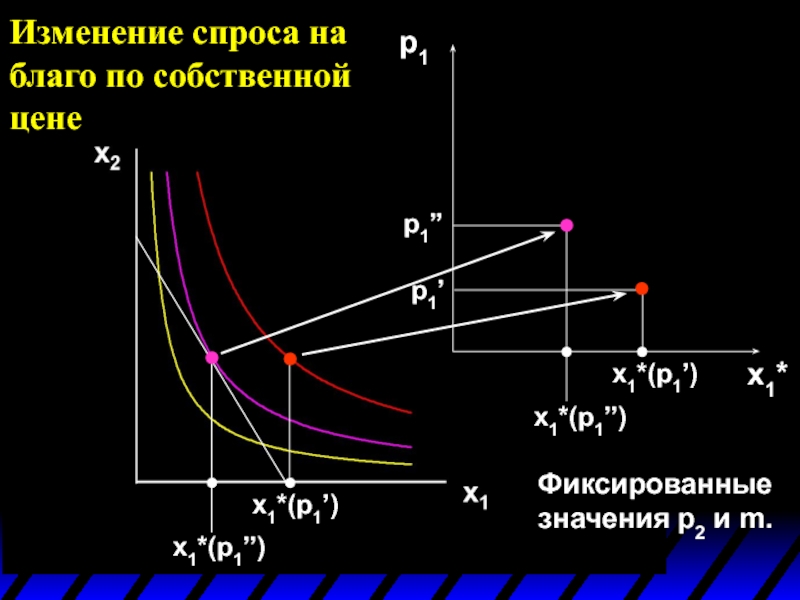
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
p1’
p1 = p1’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2
Слайд 12
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’)
p1’
p1’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2 и m.
Слайд 13
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’)
p1’
p1’’
p1 = p1’’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2
Слайд 14
x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’)
p1’
p1’’
p1 = p1’’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2
Слайд 15
x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’’)
x1*(p1’’)
p1’
p1’’
p1’’’
x1*
Изменение спроса на благо по собственной цене
Фиксированные значения p2 и m.
Слайд 16
x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’’)
x1*(p1’’)
p1’
p1’’
p1’’’
x1*
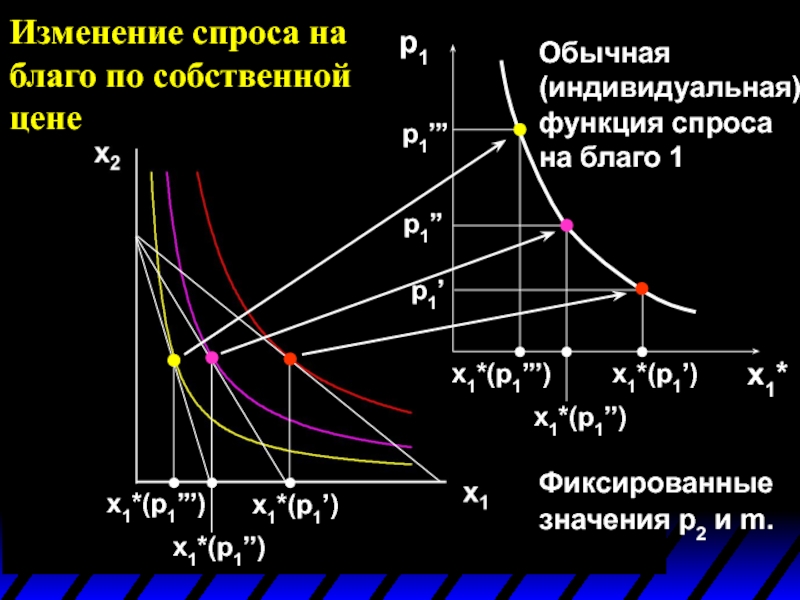
Изменение спроса на благо по собственной цене
Обычная (индивидуальная) функция спроса
на
Фиксированные значения p2 и m.
Слайд 17
x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’’)
x1*(p1’’)
p1’
p1’’
p1’’’
x1*
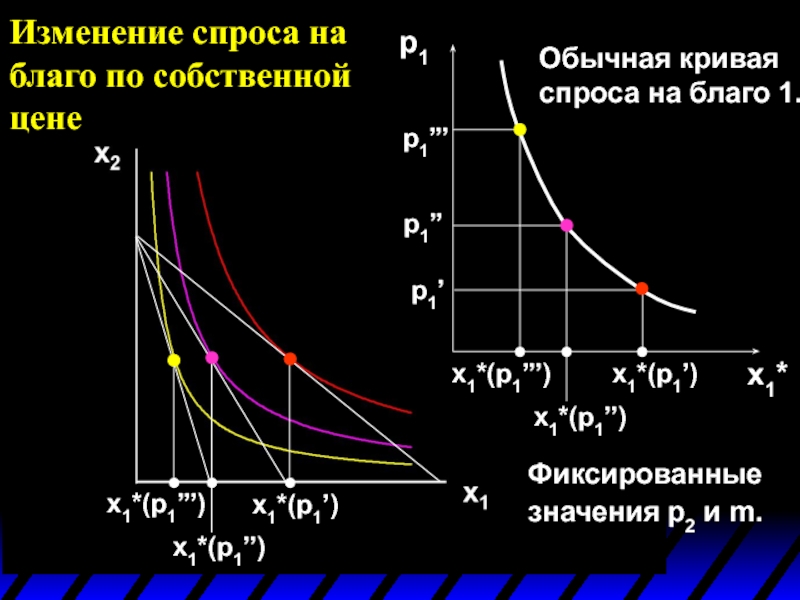
Изменение спроса на благо по собственной цене
Обычная кривая спроса на благо
Фиксированные значения p2 и m.
Слайд 18
x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*(p1’)
x1*(p1’’’)
x1*(p1’’)
p1’
p1’’
p1’’’
x1*
Изменение спроса на благо по собственной цене
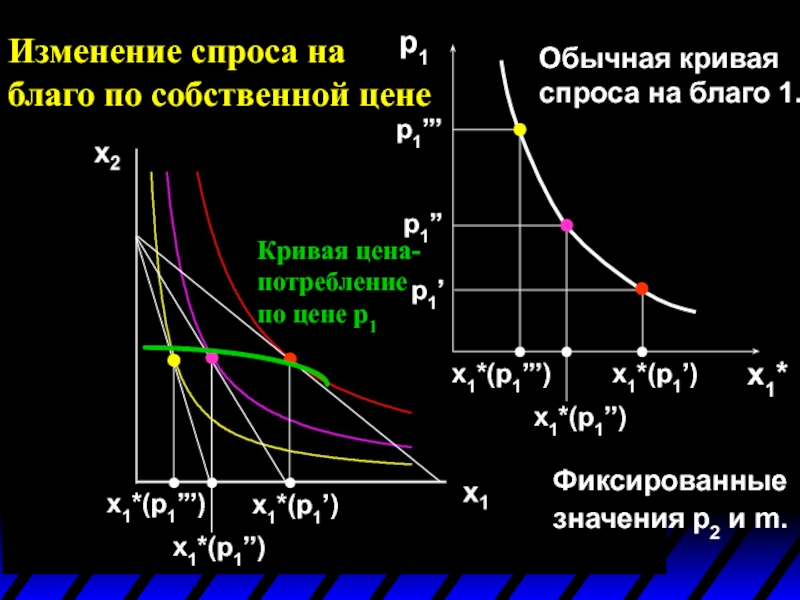
Обычная кривая спроса на благо
Кривая цена-потребление по цене p1
Фиксированные значения p2 и m.
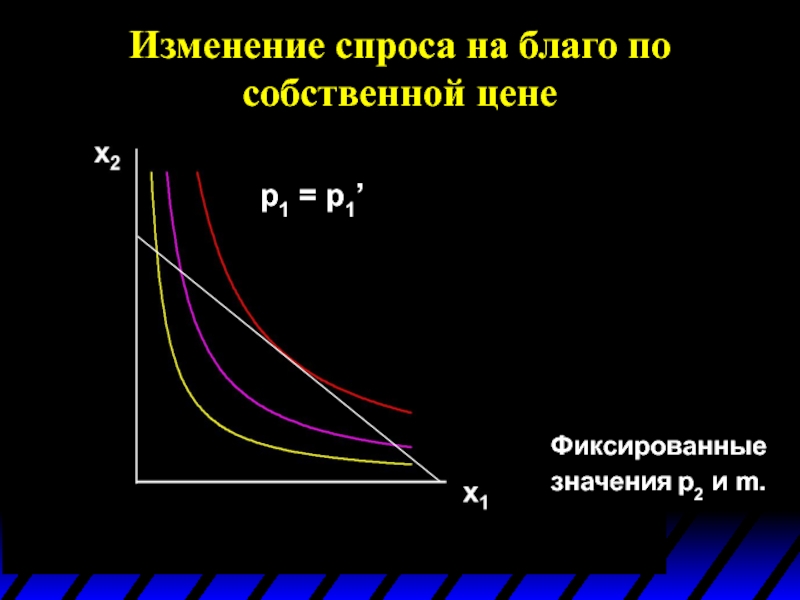
Слайд 19Изменение спроса на благо по собственной цене
Кривая, содержащая все максимизирующие полезность
График проекции кривой цена-потребление по цене p1 на ось координат x1 по перемен-ной p1 называется обычной кривой спроса (ordinary demand curve) на благо 1.
Слайд 20Изменение спроса на благо по собственной цене
Каким образом выглядит кривая цена-потребление
Слайд 21Изменение спроса на благо по собственной цене
Каким образом выглядит кривая цена-
Пусть Тогда обычные функции спроса на блага 1 и 2 по ценам p1 и p2 будут иметь вид:
Слайд 22Изменение спроса на благо по собственной цене
и
Заметим, что поскольку x2* не
Слайд 23Изменение спроса на благо по собственной цене
и
в которой вторая зависимость, характери-зующая
Слайд 24Изменение спроса на благо по собственной цене
и
В связи с тем, что
Слайд 25x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
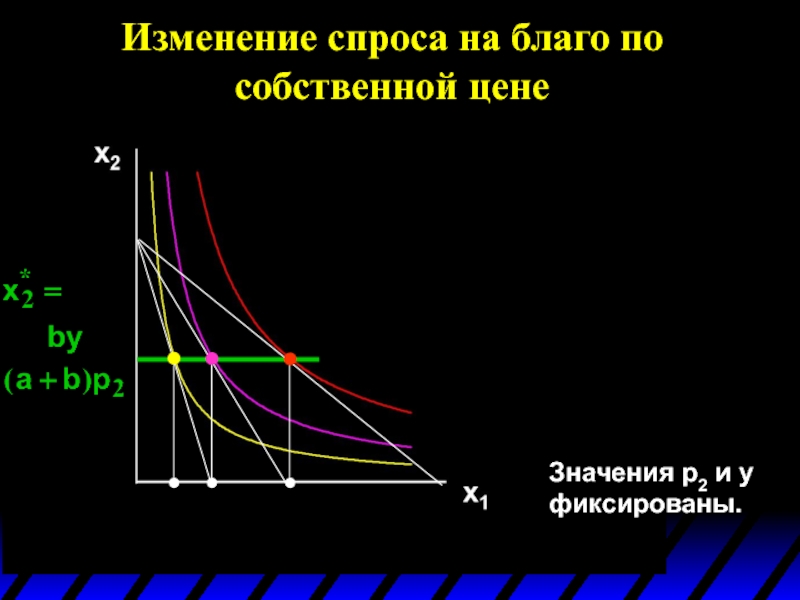
Изменение спроса на благо по собственной цене
Значения p2 и y фиксированы.
Слайд 26x1*(p1’’’)
x1*(p1’)
x1*(p1’’)
p1
x1*
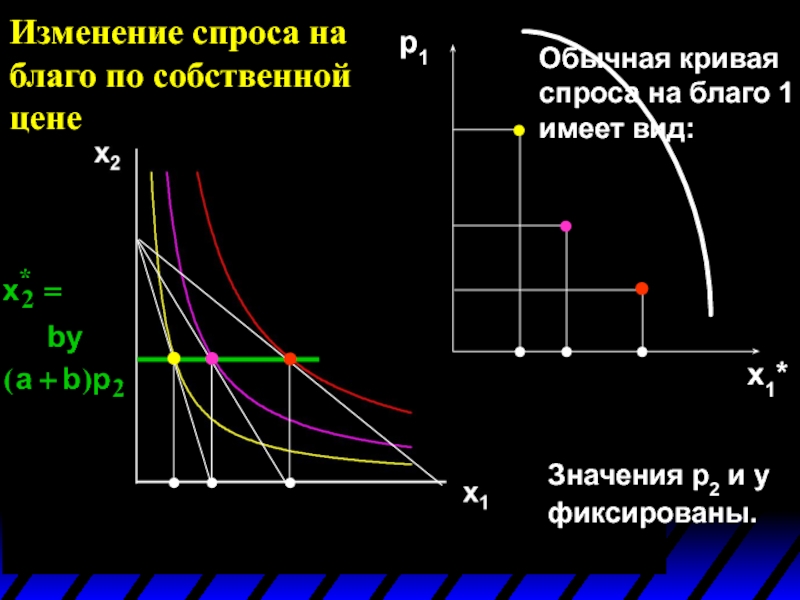
Изменение спроса на благо по собственной цене
Обычная кривая спроса на благо
Значения p2 и y фиксированы.
Слайд 27Изменение спроса на благо по собственной цене
Как выглядит кривая цена-потребление p1
Слайд 28Изменение спроса на благо по собственной цене
Как выглядит кривая цена-потребление p1
Тогда обычные кривые спроса на блага 1 и 2 выглядят следующим образом:
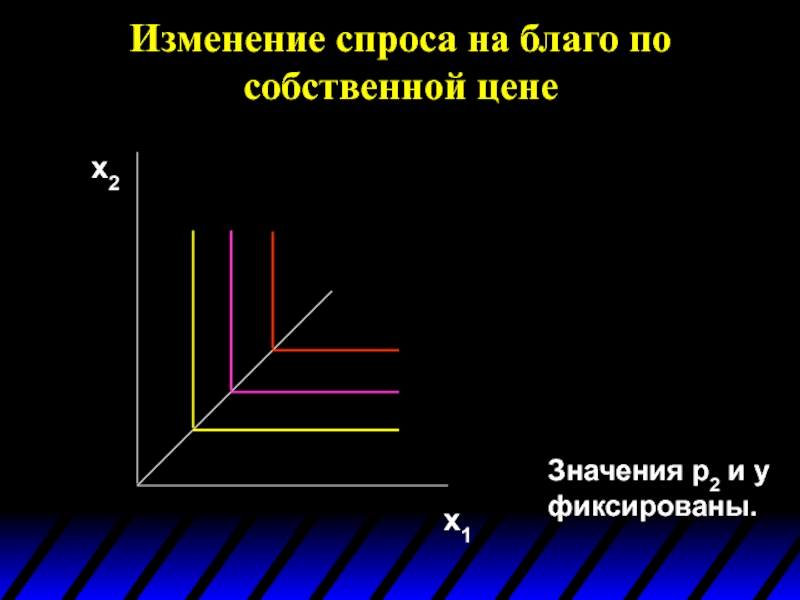
Слайд 30Изменение спроса на благо по собственной цене
При фиксированных значениях p2 и
Слайд 31Изменение спроса на благо по собственной цене
При заданных значениях p2 и
При
Слайд 32Изменение спроса на благо по собственной цене
При заданных значениях p2 и
При
При
Слайд 34p1
x1*
Значения p2 и y фиксированы.
Изменение спроса на благо по собственной
x1
x2
p1’
’
p1 = p1’
’
’
y/p2
Слайд 35p1
x1*
Значения p2 и y фиксированы.
Изменение спроса на благо по собственной
x1
x2
p1’
p1’’
p1 = p1’’
’’
’’
’’
y/p2
Слайд 36p1
x1*
Значения p2 и y фиксированы.
Изменение спроса на благо по собственной
x1
x2
p1’
p1’’
p1’’’
p1 = p1’’’
’’’
’’’
’’’
y/p2
Слайд 37p1
x1*
Кривая спроса на благо 1
Значения p2 и y фиксированы.
Изменение спроса на
x1
x2
p1’
p1’’
p1’’’
y/p2
Слайд 38Изменение спроса на благо по собственной цене
Как выглядит кривая цена-потребление p1
В этом случае обычные функции спроса на блага 1 и 2 имеют вид:
Слайд 41Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
Значения p2 и y фиксированы.
p1’
p1
’
’
Слайд 42Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
Значения p2 и y фиксированы.
p1’
p1
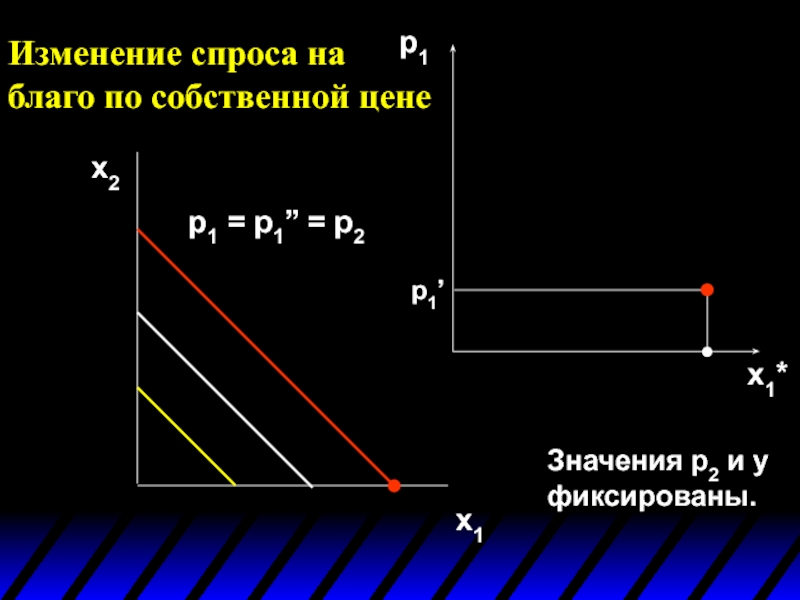
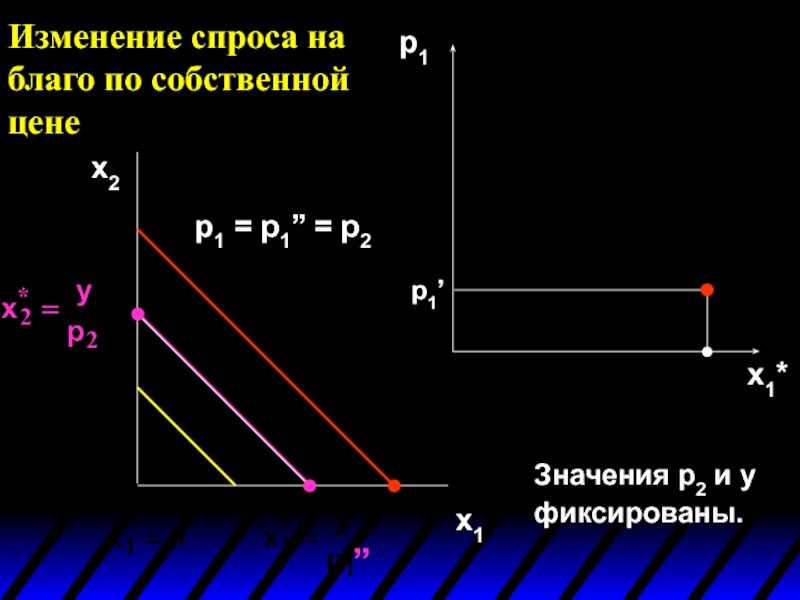
Слайд 43Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
Значения p2 и y фиксированы.
p1’
p1 = p1’’ = p2
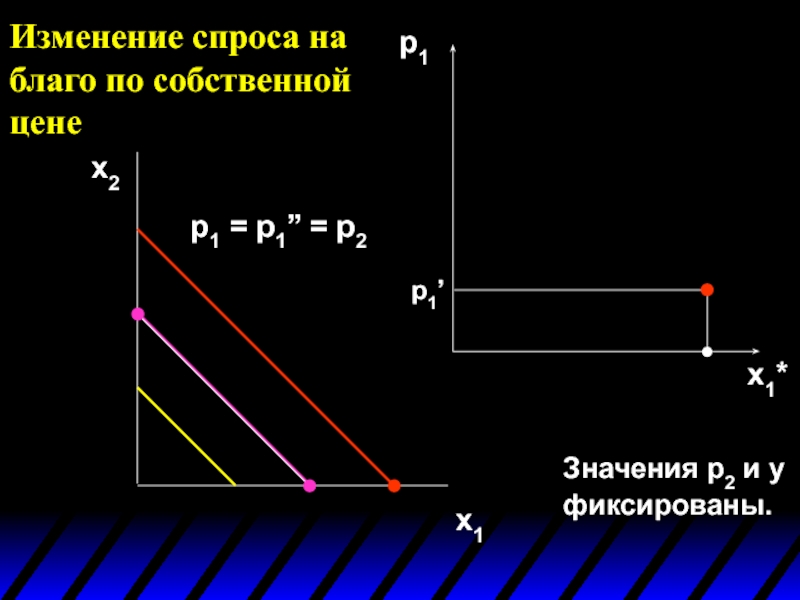
Слайд 44Значения p2 и y фиксированы.
Изменение спроса на благо по собственной
x2
x1
p1
x1*
p1’
p1 = p1’’ = p2
’’
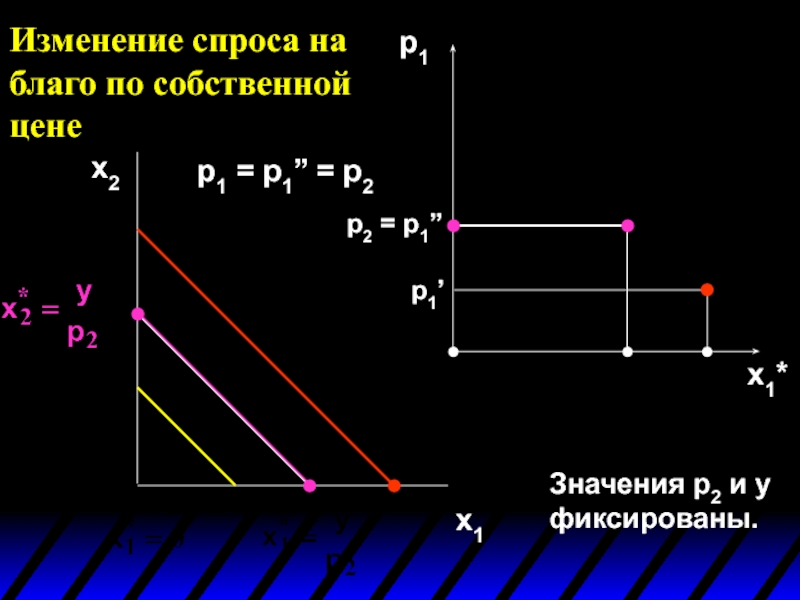
Слайд 45Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
p1’
p1 = p1’’ = p2
p2
Значения p2 и y фиксированы.
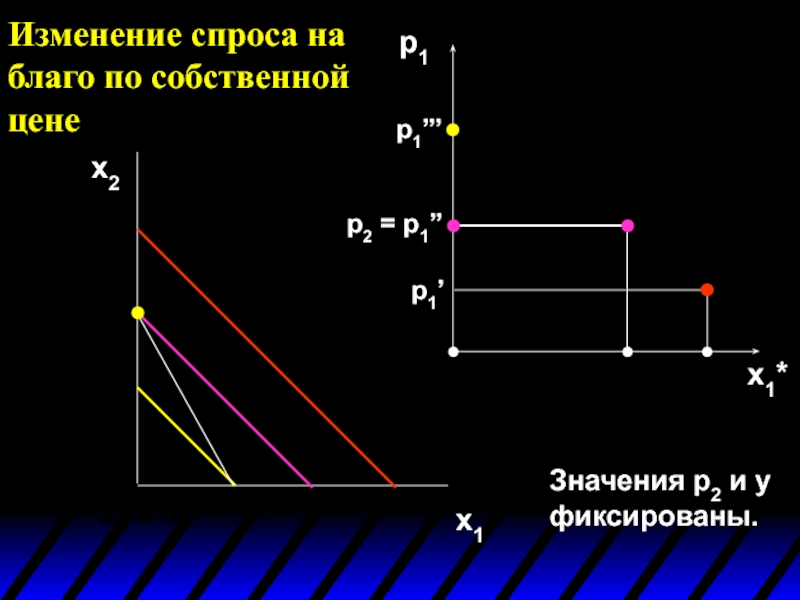
Слайд 46Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
Значения p2 и y фиксированы.
p1’
p1’’’
p2
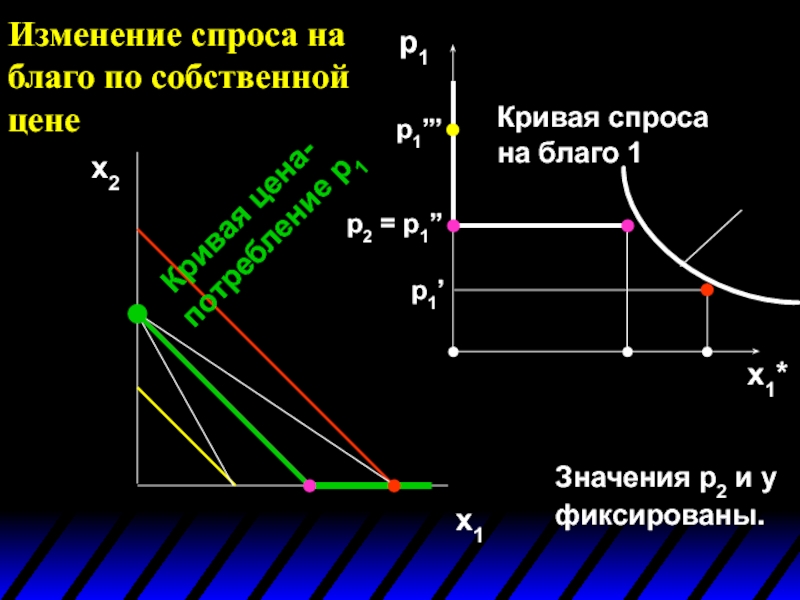
Слайд 47Изменение спроса на благо по собственной цене
x2
x1
p1
x1*
Значения p2 и y фиксированы.
p1’
p2
p1’’’
Кривая цена-потребление p1
Кривая спроса на благо 1
Слайд 48Изменение спроса на благо по собственной цене
Стандартная постановка задачи определения спроса
Однако возможна постановка и обратной задачи, а именно: определения цены, при которой заданное количество блага будет востребовано потребителем.
Слайд 49Изменение спроса на благо по собственной цене
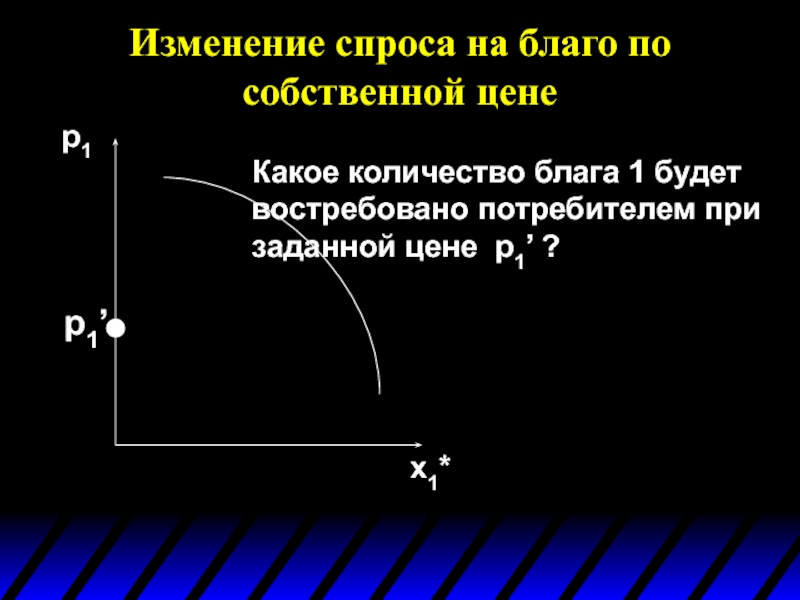
p1
x1*
p1’
Какое количество блага 1 будет
Слайд 50Изменение спроса на благо по собственной цене
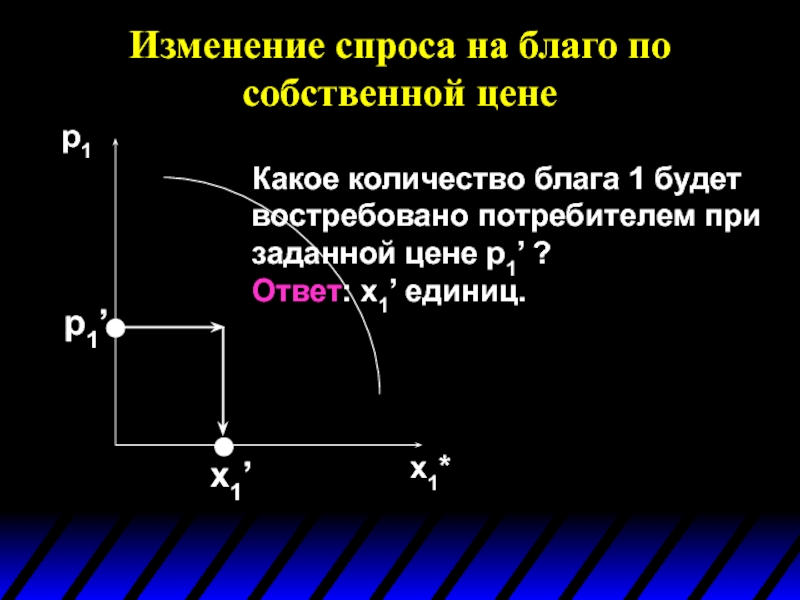
p1
x1*
p1’
Какое количество блага 1 будет
Ответ: x1’ единиц.
x1’
Слайд 51Изменение спроса на благо по собственной цене
p1
x1*
x1’
Какое количество блага 1 будет
Ответ: x1’ единиц.
Обратная постановка задачи: при какой
цене потребителем будет востребовано
x1’ единиц блага 1?
Слайд 52Изменение спроса на благо по собственной цене
p1
x1*
x1’
Какое количество блага 1 будет
Ответ: x1’ единиц.
Обратная постановка задачи: при какой
цене потребителем будет востребовано
x1’ единиц блага 1?
Ответ: p1’ .
p1’
Слайд 53Изменение спроса на благо по собственной цене
Рассматривая востребованное количество блага в
Слайд 54Изменение спроса на благо по собственной цене
В случае, когда полезность представлена
представляет собой индивидуальную функцию спроса, а:
есть обратная функция спроса.
Слайд 55Изменение спроса на благо по собственной цене
В случае, когда блага совершенно
является индивидуальной функцией спроса, а зависимость:
представляет собой обратную функцию спроса (inverse demand function).
Слайд 56Изменение спроса по доходу
Каким образом скажется на величине x1*(p1,p2,y) изменение дохода
Слайд 59Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
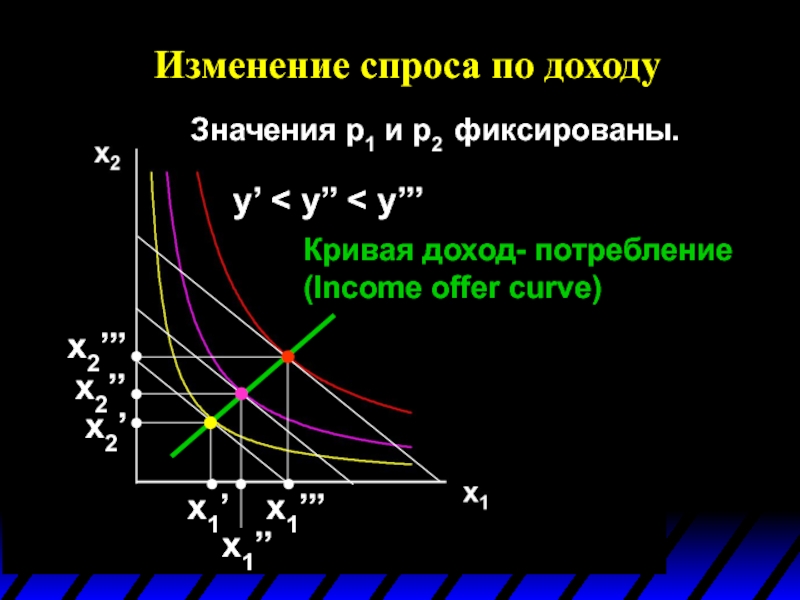
Слайд 60Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление (Income оffer curve)
Слайд 61Изменение спроса по доходу
График зависимости между величиной спроса потребителя на благо
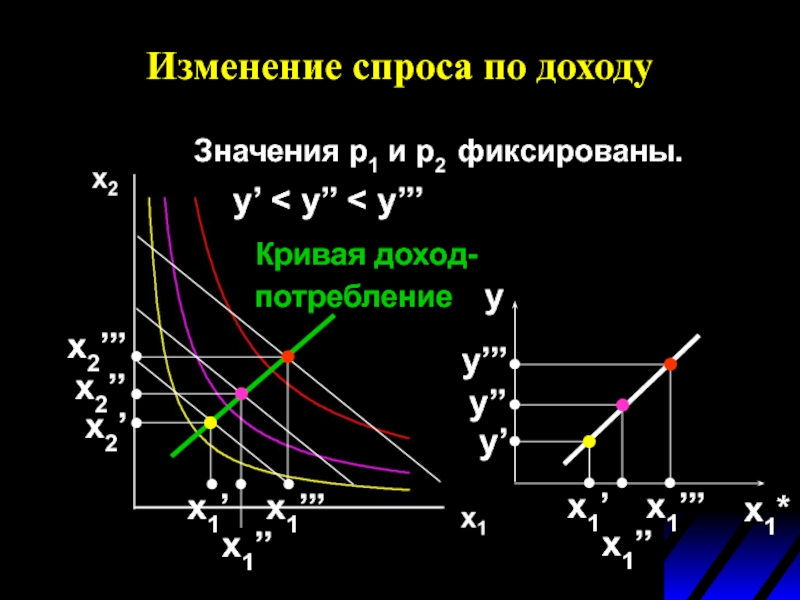
Слайд 62Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
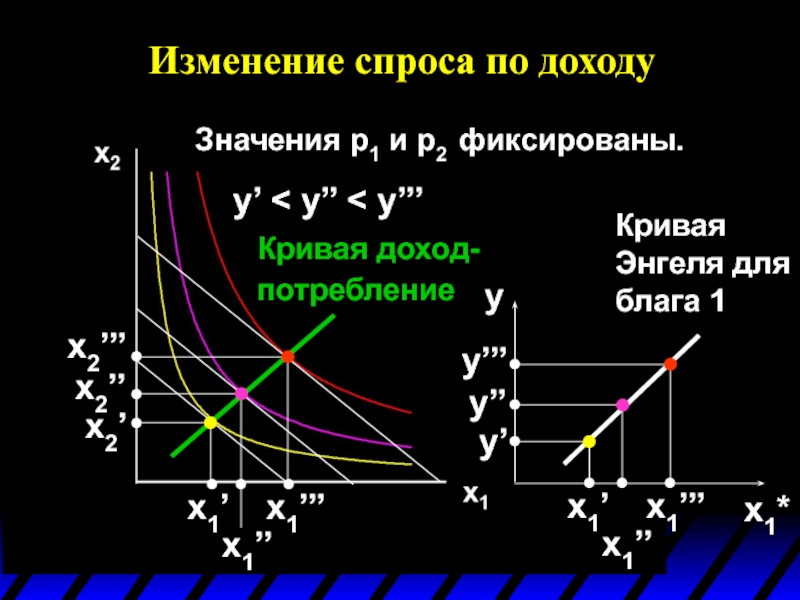
Слайд 63Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
x1*
y
x1’’’
x1’’
x1’
y’
y’’
y’’’
Слайд 64Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
x1*
y
x1’’’
x1’’
x1’
y’
y’’
y’’’
Кривая Энгеля для блага 1
Слайд 65Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
x2*
y
x2’’’
x2’’
x2’
y’
y’’
y’’’
Слайд 66Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
x2*
y
x2’’’
x2’’
x2’
y’
y’’
y’’’
Кривая Энгеля для блага 2
Слайд 67Изменение спроса по доходу
Значения p1 и p2 фиксированы.
y’ < y’’
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход- потребление
x1*
x2*
y
y
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
y’
y’’
y’’’
y’
y’’
y’’’
Кривая Энгеля для блага 2
Кривая Энгеля для блага 1
Слайд 68Изменение по доходу в случае предпочтений Кобба-Дугласа
Пример определения вида уравнений Энгеля
Уравнения спроса на блага имеют вид:
Слайд 69Изменение по доходу в случае предпочтений Кобба-Дугласа
Перепишем уравнения спроса так,
Кривая Энгеля для блага 1
Кривая Энгеля для блага 2
Слайд 70Изменение по доходу в случае предпочтений Кобба-Дугласа
y
y
x1*
x2*
Кривая Энгеля для блага 1
Кривая
Слайд 71Изменение спроса по доходу в случае взаимодополняемых благ
В случае взаимодополняемых благ
Функции спроса на блага 1 и 2 имеют вид:
Слайд 72Изменение спроса по доходу в случае взаимодополняемых благ
Перепишем уравнения спроса
Кривая Энгеля для блага 1
Кривая Энгеля для блага 2
Слайд 77Изменение дохода
x1
x2
y’ < y’’ < y’’’
x1’’
x1’
x2’’’
x2’’
x2’
x1’’’
x1*
y
y’
y’’
y’’’
Кривая Энгеля для блага 1
x1’’’
x1’’
x1’
Цены p1
Слайд 78Изменение дохода
x1
x2
y’ < y’’ < y’’’
x1’’
x1’
x2’’’
x2’’
x2’
x1’’’
x2*
y
x2’’’
x2’’
x2’
y’
y’’
y’’’
Кривая Энгеля для блага 2
Цены p1
Слайд 79Изменение дохода
x1
x2
y’ < y’’ < y’’’
x1’’
x1’
x2’’’
x2’’
x2’
x1’’’
x1*
x2*
y
y
x2’’’
x2’’
x2’
y’
y’’
y’’’
y’
y’’
y’’’
Кривая Энгеля для блага 2
Кривая
x1’’’
x1’’
x1’
Цены p1 и p2 фиксированы.
Слайд 80Изменение дохода
x1*
x2*
y
y
x2’’’
x2’’
x2’
y’
y’’
y’’’
y’
y’’
y’’’
x1’’’
x1’’
x1’
Кривая Энгеля для блага 2
Кривая Энгеля для блага 1
Цены p1 и p2 фиксированы.
Слайд 81Изменение спроса по доходу для благ совершенных заменителей
Определим аналитический вид
Функции спроса на блага 1 и 2 имеют вид:
Слайд 83Изменение спроса по доходу для благ совершенных заменителей
Для дальнейшего анализа
Слайд 86Изменение спроса по доходу для благ совершенных заменителей
y
y
x1*
x2*
0
Кривая Энгеля для блага
Кривая Энгеля для блага 2
Слайд 87Изменение спроса по доходу
В рассмотренных выше примерах кривые Энгеля представляли собой
Оказывается, что кривая Энгеля представи-ма в форме линейной зависимости в случае, когда отношение предпочтения потребителя является гомотетичным (homothetic).
Слайд 88Гомотетичное отношение предпочтения
Отношение предпочтения называется гомотетичным тогда и только тогда,
Гомотетичность отношения предпочтения означает, что предельная норма замены благ MRS неизменна вдоль лучей, исходящих из начала координат.
(x1,x2) (y1,y2) (kx1,kx2) (ky1,ky2).
Слайд 89Эффекты дохода - пример негомотетичного предпочтения
Квазилинейные предпочтения не являются гомотетичными. В
следующего вида:
Слайд 90Квазилинейные кривые безразличия
x2
x1
Каждая кривая безразличия может быть представлена как вертикальное смещение
Каждая кривая безразличия пересекает обе оси координат.
Слайд 94
Изменения дохода в случае квазилинейного предпочтения
x2
x1
x1*
x2*
y
y
x1
~
Кривая Энгеля для блага 2
Кривая Энгеля для блага 1
Слайд 95Характеристики изменения спроса
Изменения спроса в соответствии со значениями цен и дохода
Однако изменение спроса можно исследо-вать в терминах предельных (приростных) величин, т.е. анализируя приращения величин спроса и объясняющей переменной (цены или дохода).
Слайд 96Гомотетичные предпочтения: функциональное представление
Функция f:Rn+R называется однородной степени “k”, если для
Функция f:Rn+R называется линейно однородной или однородной степени 1, если для любого числа λ>0 на всей области определения функции выполнено f(λx)= λf(x).
Функция f:Rn+R называется однородной нулевой степени (однородной степени 0), если для любого числа λ>0 на всей области определения функции выполнено f(λx)= f(x).
Слайд 97Гомотетичные предпочтения: функциональное представление
Функция f:RnR называется гомотетичной, если она представима в
Если функция полезности U(x) является гомотетичной, то это означает, что она представима в виде монотонно возрастающего преобразования линейно однородной функции полезности.
Слайд 98Характеристики изменения спроса
Обозначим через xi*(pi) функцию, задающую кривую спроса, т.е. xi*(pi)=xi*(p,y)
Соответственно, через xi*(y) обозначим функцию, задающую кривую Энгеля для товара i, т.е. xi*(y)=xi*(p,y) при фиксированных значениях цен товаров.
Слайд 99Характеристики изменения спроса
При изменении цены товара i на величину
Приходящееся на единицу изменения цены приращение спроса составит xi*/pi. Данная величина показывает (служит оценкой) изменение(я) спроса в точке xi*(pi) в резуль-тате изменения цены на одну единицу.
Если описывающая кривую спроса функция дифференцируема, то возникающее в точке xi*(pi) в результате изменения цены приращение спроса будет равно xi*/ pi .
Слайд 100Характеристики изменения спроса
Аналогично, при изменении дохода потреби-теля на величину y =
Приращение спроса на единицу изменения дохода составит xi*/y. Данная величина служит оценкой изменения спроса в точке xi*(y) в результате изменения дохода на одну единицу.
Если описывающая кривую Энгеля функция дифференцируема, то в результате измене-ния цены приращение спроса в точке xi*(y) составит xi*/ y .
Слайд 101Эффект дохода
Если для блага (товара) i выполняется xi*/ y>0 (xi*/y
Тем самым, если рассматриваемое благо является нормальным, то соответствующая кривая Энгеля имеет положительный наклон.
Слайд 102Эффект дохода
Благо, спрос на которое падает с ростом дохода потребителя,
Таким образом, в случае малоценного блага кривая Энгеля имеет отрицательный наклон.
Слайд 103Изменение дохода: блага 1 и 2 нормальные
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
Кривая доход-
потребление
x1*
x2*
y
y
x1’’’
x1’’
x1’
x2’’’
x2’’
x2’
y’
y’’
y’’’
y’
y’’
y’’’
Кривая Энгеля для блага
Кривая Энгеля для блага 1
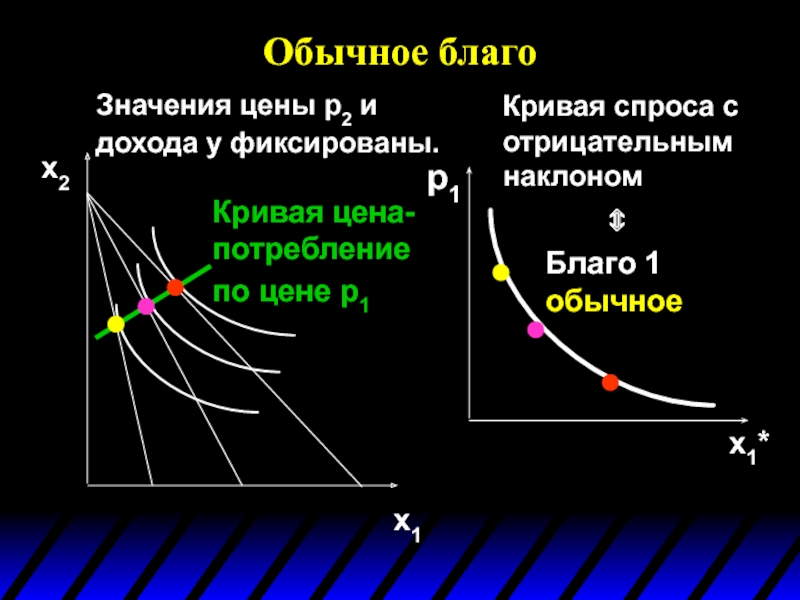
Слайд 106Обычное благо
Благо (товар) i называется обычным, если с увеличением его собственной
Таким образом, кривая спроса обычного блага имеет всюду отрицательный наклон.
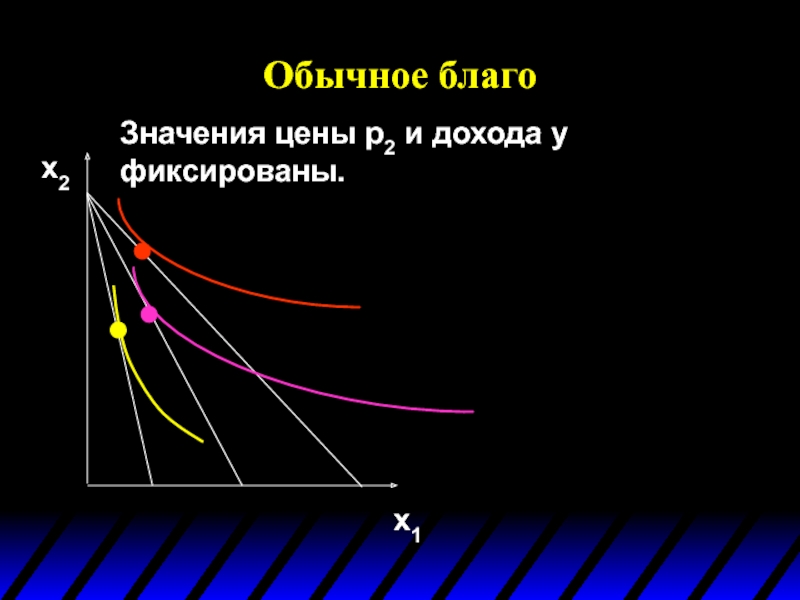
Слайд 107Обычное благо
Значения цены p2 и дохода y фиксированы.
x1
x2
Кривая цена-потребление по цене
Слайд 108Обычное благо
Значения цены p2 и дохода y фиксированы.
x1
x2
Кривая цена-потребление
x1*
Кривая спроса с отрицательным наклоном
Благо 1
oбычное
⇔
p1
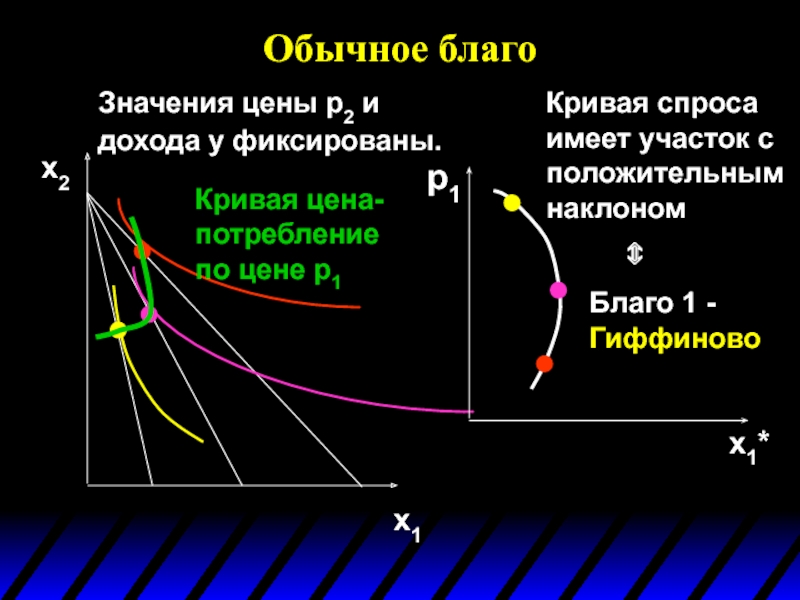
Слайд 109Гиффиновы блага (Giffen Goods)
Если при некоторых значениях цены блага спрос на
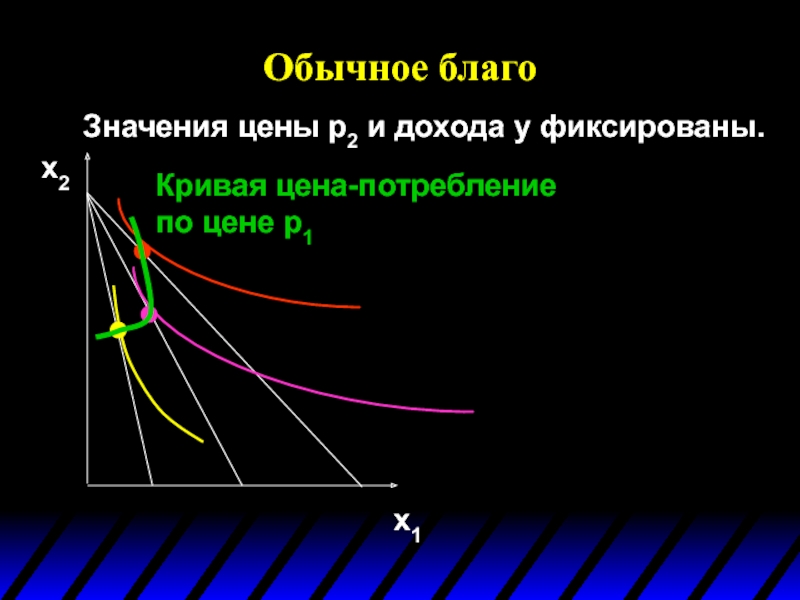
Слайд 111Oбычное благо
Значения цены p2 и дохода y фиксированы.
x1
x2
Кривая цена-потребление по
Слайд 112
Oбычное благо
Значения цены p2 и дохода y фиксированы.
x1
x2
Кривая цена-потребление
x1*
Кривая спроса имеет участок с положительным наклоном
Благо 1 -
Гиффиново
⇔
p1
Слайд 113Перекрестные ценовые эффекты
(Cross-Price Effects)
В общем случае индивидуальный спрос на то-вар i
Пусть n=2. Тогда, если возрастание цены p2
увеличивает спрос на благо 1, то благо 1 является валовым заменителем (gross substitute) блага 2.
сокращает спрос на благо 1, то благо 1 является валовым дополняющим продуктом (gross complement) блага 2.
Слайд 114Перекрестные ценовые эффекты
Случай совершенных взаимодополнящих благ:
Тем самым имеем
Таким образом, благо 2
Слайд 115Перекрестные ценовые эффекты
p1
x1*
p1’
p1’’
p1’’’
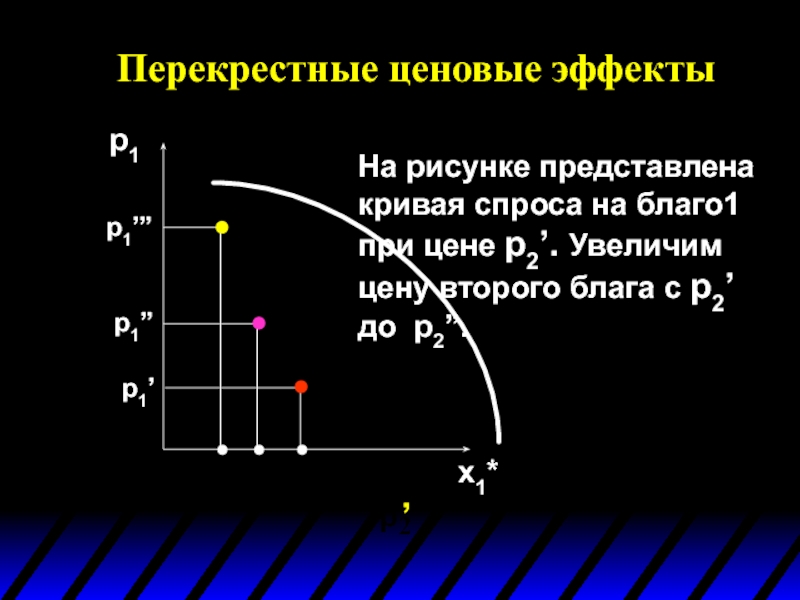
На рисунке представлена кривая спроса на благо1 при
Слайд 116Перекрестные ценовые эффекты
p1
x1*
p1’
p1’’
p1’’’
Увеличив цену блага 2 с p2’ до p2’’,
Слайд 118Перекрестные ценовые эффекты
В случае функции полезности Кобба-Дугласа:
откуда следует, что
Т.о., благо
Слайд 119Кривые Торнквиста
Рассматривается кривая, которая описывает изменение спроса на потребительские товары в
Обозначим доход потребителя через y, величину предъявляемого спроса через x.
В соответствии с конфигурацией кривой спроса выделяются три группы товаров (продуктов), присутствующих на потребительском рынке.
Слайд 120Кривые Торнквиста
Особенности спроса на предметы (товары) первой необходимости состоят в том,
физический объем потребления товаров данной группы ограничен и, соответственно, спрос на них имеет насыщение;
товары данной группы удовлетворяют первичные потребности и потому в бюджете потребителя расходы на них имеют перво-очередной приоритет, т.е., спрос на них предъявляется при любом, в том числе и низком, уровне дохода.
Товары первой необходимости
Слайд 121Кривые Торнквиста
Товары первой необходимости
Функция спроса на товары данной группы имеет вид:
y - доход потребителя,
x1 - объем спроса на товары первой
необходимости,
a1, c1 - параметры зависимости, причем
a1>0, c1>0.
Слайд 122Кривые Торнквиста
Особенности спроса на предметы длительного пользования состоят в том, что:
физический
спектр товаров, образующих данную группу, существенно шире, чем спектр группы товаров первой необходимости;
спрос на товары данной группы предъявля-ется только после того, как достигнут некото-рый уровень удовлетворения потребности в товарах первой необходимости.
Предметы длительного пользования
Слайд 123Кривые Торнквиста
Предметы длительного пользования
Функция спроса на товары данной группы имеет
, где
y - доход потребителя, y M2,
x2 - объем спроса на предметы длительного
пользования,
a2, c2, M2 - параметры зависимости, причем
a2>a1>0, c2>0, M2 >0.
Слайд 124Кривые Торнквиста
Особенности спроса на предметы роскоши состоят в том, что:
спрос на
по мере роста дохода спрос на товары данной группы неограниченно возрастает.
Предметы роскоши
Слайд 125Кривые Торнквиста
Предметы длительного пользования
Функция спроса на товары данной группы имеет
, где
y - доход потребителя, y M3,
x3 - объем спроса на предметы роскоши,
a3, c3, M3 - параметры зависимости, причем
a3>0, c3>0, M3>M2>0.