- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эконометрика. Методология VAR презентация
Содержание
- 1. Эконометрика. Методология VAR
- 2. Методология VAR
- 3. (1) экономика – это наука, (2)
- 4. Комиссия Коулса: Период с 1943 г.
- 5. Развитие соответствующих математических и статистических методов не
- 6. Значительное место в исследованиях под эгидой Комиссии
- 7. Cпецификация модели производится с априорным разделением переменных
- 8. Собственно эконометристы остаются отделенными от выбора модели,
- 9. Методология Комиссии Коулса: критика
- 10. Для преодоления указанных недостатков методологии Комиссии были
- 11. Методология LSE (Sargan, Hendry) Акценты смещаются с
- 12. Методология LSE Это приводит к статистической модели
- 13. Методология VAR (Sims) Разделение изменений
- 14. В основе методологии VAR
- 15. Простая VAR(1) для двух рядов (k =
- 16. Пример Эту VAR можно записать в
- 17. При этом, Корни уравнения лежат
- 18. Поэтому можно записать: Тем
- 19. Однако: Из-за того, что общем случае
- 20. “Фундаментальные” инновации Для преодоления указанного затруднения
- 21. В примере с двумерной VAR(1):
- 22. Импульсные функции отклика (impulse
- 23. Проблема отыскания матрицы D Если матрица
- 24. Отсюда: Для нахождения четырех неизвестных
- 25. упорядочивание инноваций в системе. Пусть фундаментальная инновация
- 26. Пример двумерной VAR(1) u1t u2t ?
- 27. Тогда Обозначим
- 28. Пусть в приведенной VAR(1) ковариационная матрица ошибок
- 29. Изменим теперь упорядочение инноваций Пусть
- 30. Структурная VAR имеет вид: Представляем:
- 31. Резюме: При первом упорядочении инноваций:
- 32. Рекурсивная система
- 33. Сравним функции отклика переменных y1t и y2t
- 34. При этом мы получаем измененную реализацию
- 35. Таким образом, мы получили следующие значения функций
- 36. При втором упорядочении Получаются следующие значения
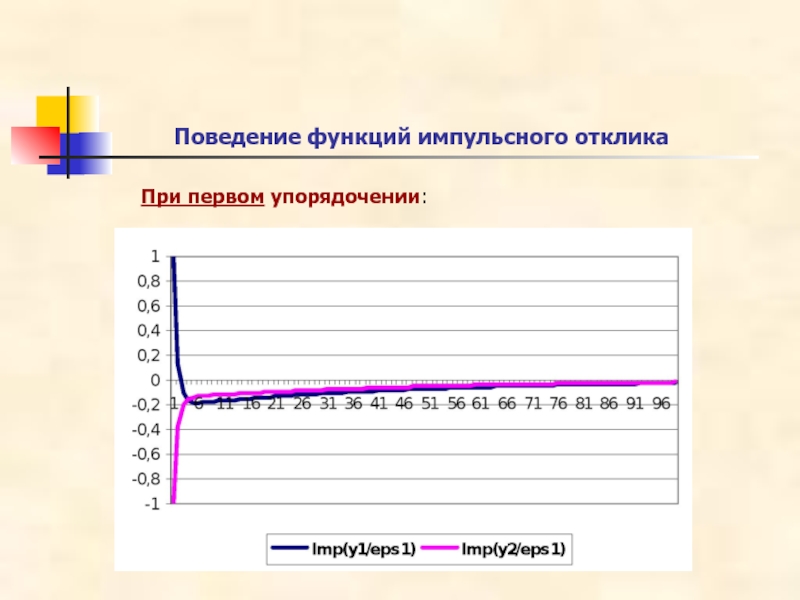
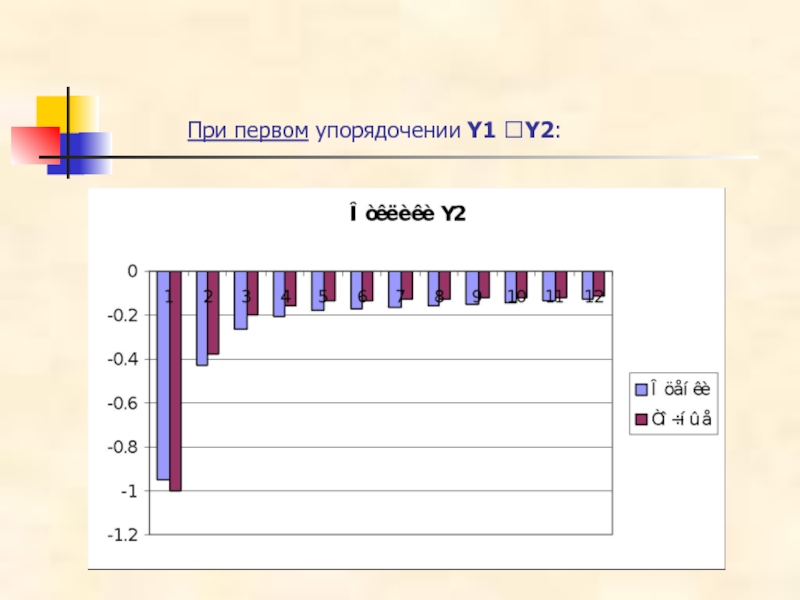
- 37. Поведение функций импульсного отклика При первом упорядочении:
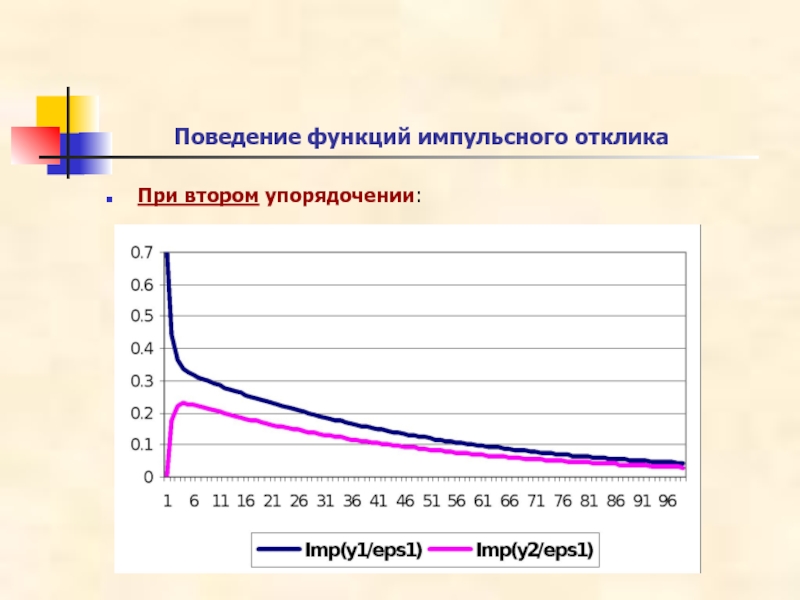
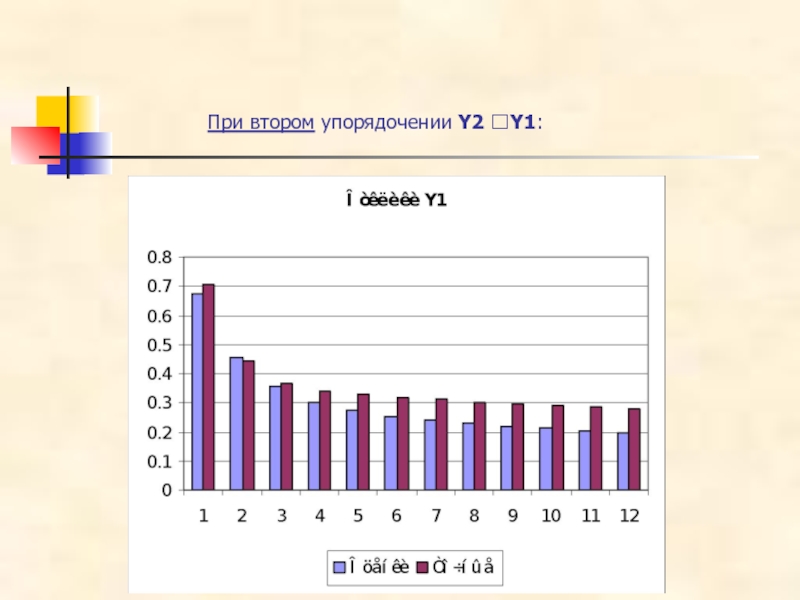
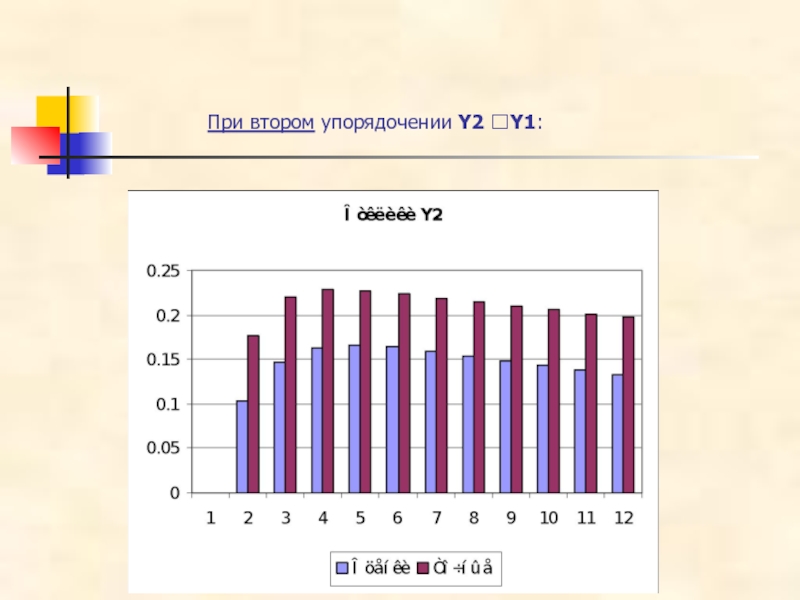
- 38. При втором упорядочении: Поведение функций импульсного отклика
- 39. Проблема:
- 40. В нашем примере: (impulse_new.wf1) (impulse_new_reord.wf1)
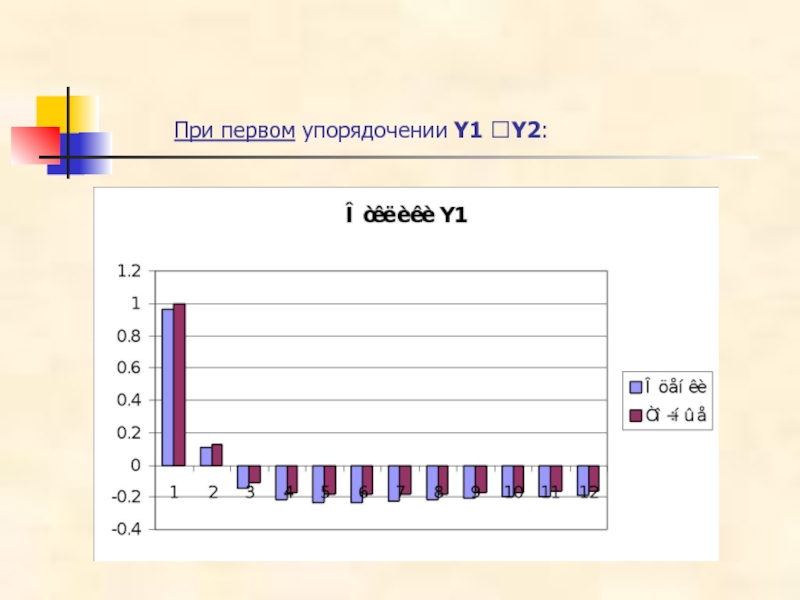
- 41. При первом упорядочении Y1 ?Y2:
- 42. При первом упорядочении Y1 ?Y2:
- 43. При втором упорядочении Y2 ?Y1:
- 44. При втором упорядочении Y2 ?Y1:
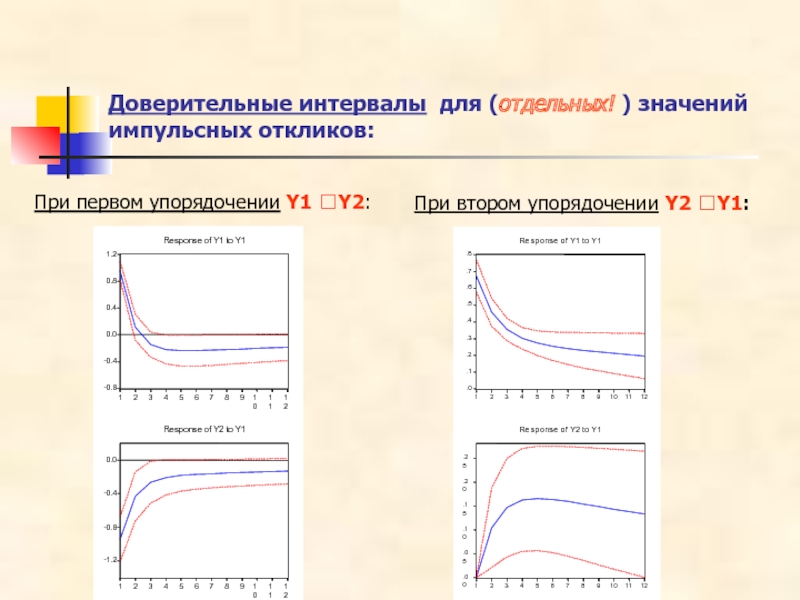
- 45. Доверительные интервалы для (отдельных! ) значений импульсных
- 46. Замечание Столь существенное различие в поведении функций
- 47. В общем случае предполагают, что структурная модель
- 48. Приведенная форма: Структурная форма:
- 49. Проблема идентификации структурных уравнений по приведенной форме
- 50. Матрица симметрична, и поэтому достаточно
- 51. Разложение Холецкого (Cholesky factorization) Методология Симса, которую
- 52. Факторизация матрицы D
- 53. Приравняем: Тогда (Нижняя треугольная матрица имеет обратную, которая также является нижней треугольной)
- 54. Резюме Если наложить на матрицы A и
- 55. Рекурсивная система В первое уравнение с
- 56. Вернемся к k -мерной VAR(p) Приведенная форма:
- 57. k -мерная VAR(p)
- 58. и если
- 59. Матрицу D можно представить в виде При
- 60. Разложение Холецкого (Cholesky factorization)
- 62. Декомпозиция (разложение) дисперсии ошибок прогнозов (variance
- 63. Ошибка прогноза по VAR на один шаг
- 64. Но dj – j-й столбец матрицы D
- 65. Дисперсия ошибки прогноза на один шаг вперед
- 66. Дисперсия ошибки прогноза на один шаг вперед
- 67. – составляющая ошибки прогноза
- 68. – составляющая ошибки прогноза на один
- 69. – дисперсия ошибки прогноза на один
- 70. – дисперсия ошибки прогноза на один
- 71. Вернемся к двумерной VAR(1) При упорядочении Y1 ? Y2
- 72. – доля дисперсии ошибки прогноза на один
- 73. Ошибка прогноза по VAR на h шагов
- 74. Ошибка прогноза по VAR на h шагов
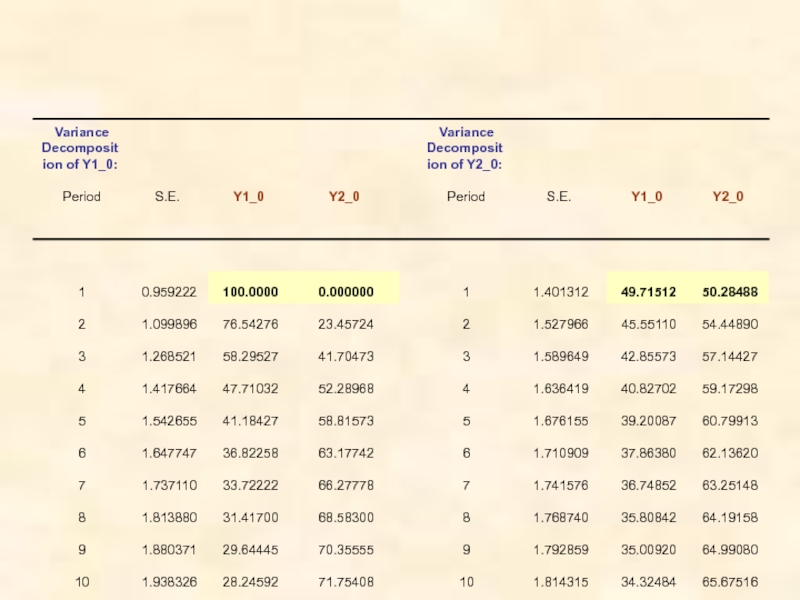
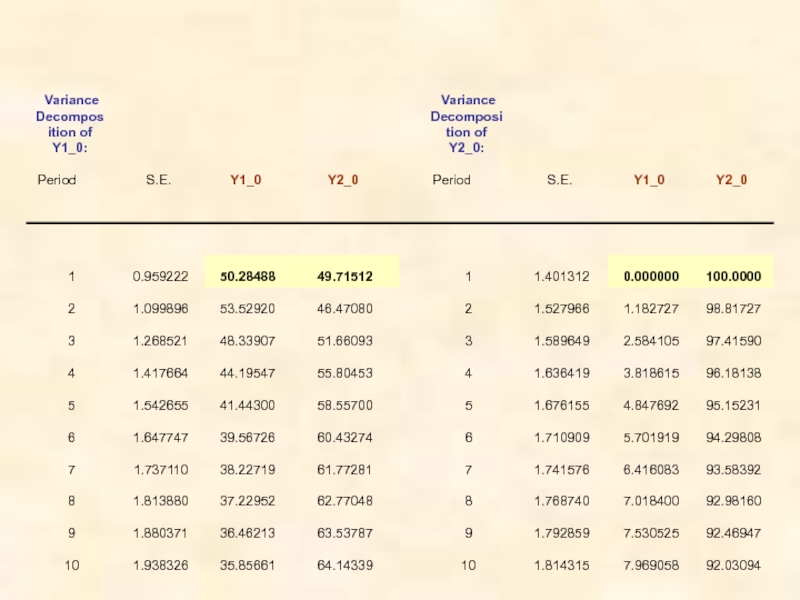
- 75. Декомпозиция дисперсии ошибок прогнозов Обычно
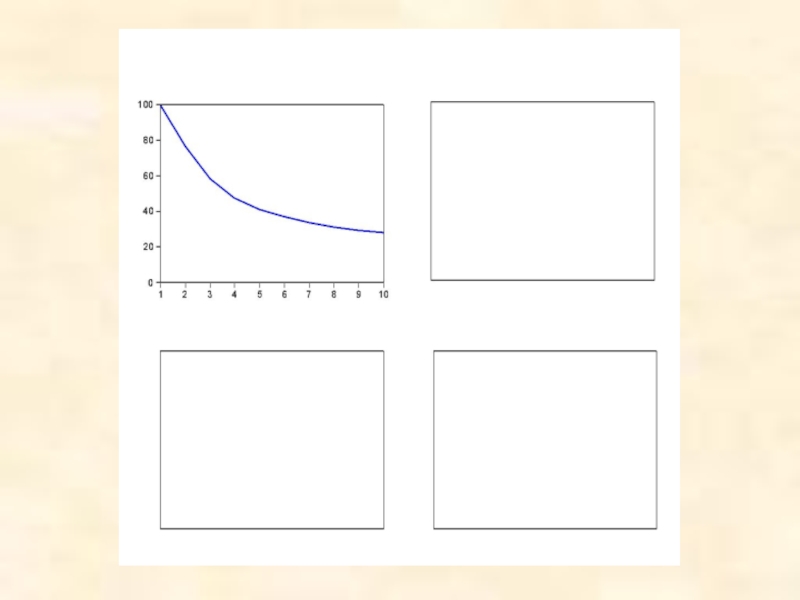
- 76. Cholesky Ordering: Y1 Y2
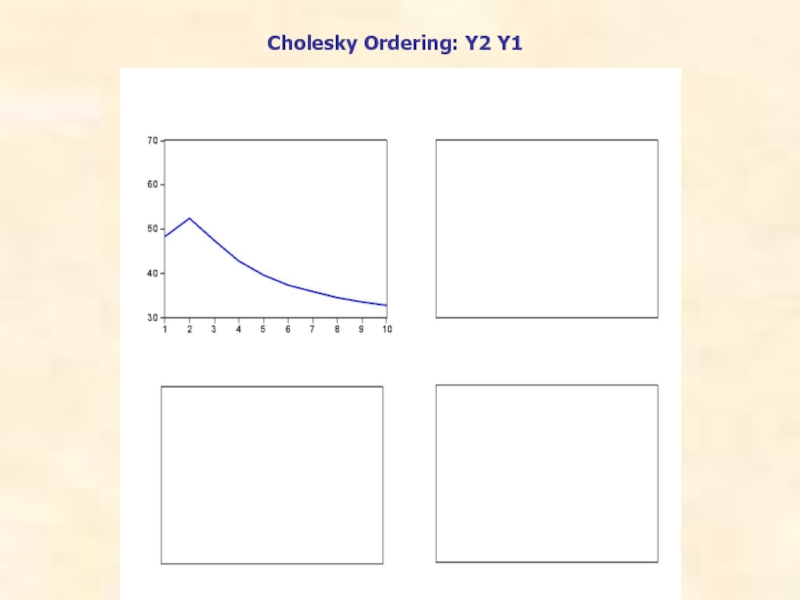
- 78. Cholesky Ordering: Y2 Y1
- 80. Оценивание SVAR в EViews При первом
- 81. Таким образом, при первом упорядочении SVAR (структурная VAR) принимает вид:
- 82. В рекурсивной структуре, полученной с использованием изложенного
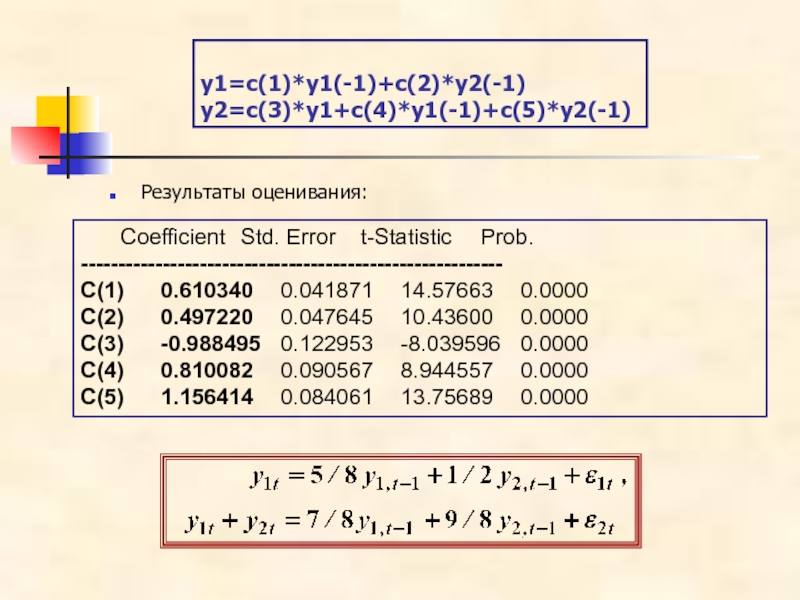
- 83. y1=c(1)*y1(-1)+c(2)*y2(-1) y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1) Результаты оценивания: Coefficient Std. Error t-Statistic Prob. --------------------------------------------------------- C(1) 0.610340 0.041871 14.57663 0.0000 C(2) 0.497220 0.047645 10.43600 0.0000 C(3) -0.988495 0.122953 -8.039596 0.0000 C(4) 0.810082 0.090567 8.944557 0.0000 C(5) 1.156414 0.084061 13.75689 0.0000
- 84. EViews: Оценивание матриц A и B
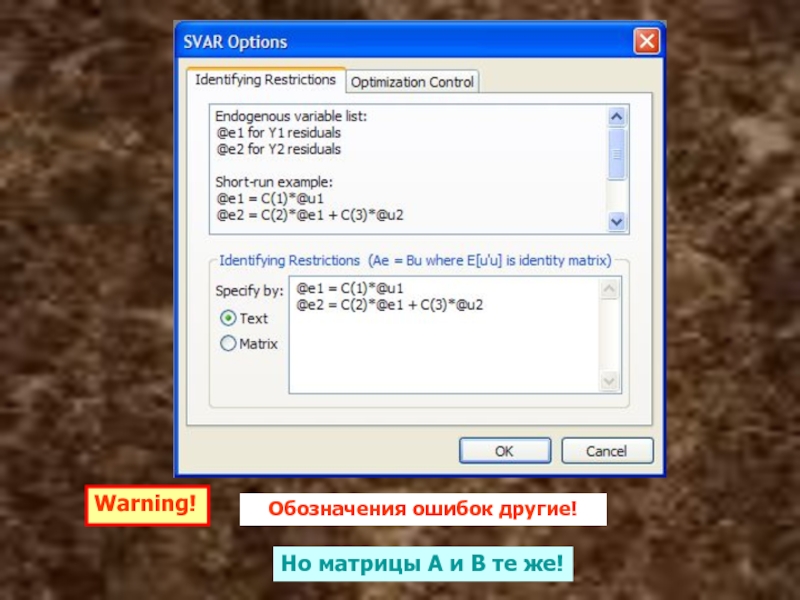
- 85. Warning! Обозначения ошибок другие! Но матрицы A и B те же!
- 86. Model: Ae = Bu where E[uu']=I
- 87. Замечания Принимая различные порядки последовательного вхождения переменных,
- 88. Пример. В модели двумерной VAR переменная y1t
- 89. Пример (продолжение) Упорядочение y2t ? y1t
Слайд 3(1) экономика – это наука,
(2) в этой науке очень важен
1932 г. – учреждение Комиссии Коулса
(The Cowles Commission for Research in Economics)
1932 г. – решение об издании журнала “Econometrica”
1933 г. (январь) – выход первого номера журнала
Два принципа журнала:
Слайд 4Комиссия Коулса: Период с 1943 г. – Джейкоб Маршак
Методы исследования должны быть обусловлены следующими характеристиками экономических данных и экономической теории:
Теория есть система одновременных уравнений, а не отдельное уравнение;
некоторые из этих уравнений включают "случайные" составляющие, отражающие многочисленные неустойчивые причины, в дополнение к нескольким "систематическим.
Многие данные выражены в виде временных рядов, причем последующие события зависят от предыдущих.
Многие опубликованные данные относятся скорее к агрегатам, а не к отдельным субъектам.
Слайд 5Развитие соответствующих математических и статистических методов не менее важно, чем получение
Применение математических результатов в практических исследованиях сопровождается также и обратным движением : возникновение новых ситуаций в процессе практической работы ставит и новые задачи перед математиками.
Комиссия Коулса
Слайд 6Значительное место в исследованиях под эгидой Комиссии заняла разработка моделей и
Цель –количественный анализ влияния изменений в переменных, контролируемых неким монетарным "полисмейкером“, на макроэкономические переменные, представляющие конечные цели этого полисмейкера.
Такой анализ предусматривает:
спецификацию и идентификацию теоретической модели,
оценивание параметров,
расчет динамических свойств модели с особым акцентом на долговременные свойства,
симуляцию динамической модели,
анализ последствий различных политик.
Комиссия Коулса
Слайд 7Cпецификация модели производится с априорным разделением переменных на экзогенные и эндогенные.
Идентификация достигается как результат накладывания большого количества ограничений.
При выявлении тех или иных отклонений от стандартных предположений метода наименьших квадратов модифицируется не модель, а метод оценивания.
Базовая симуляция обычно производится на основе имеющейся выборки; результаты базовой симуляции сравниваются с результатами, полученными в альтернативной симуляции, основанной на модификации соответствующих экзогенных переменных.
Анализ альтернативных политик базируется на динамических мультипликаторах.
Комиссия Коулса: системы одновременных уравнений
(simultaneous equations model – SEM)
Слайд 8Собственно эконометристы остаются отделенными от выбора модели, который является прерогативой экономистов,
Методология Комиссии Коулса
Слайд 9 Методология Комиссии Коулса: критика Лукаса и Симса (Lucas (1978),
Лукас:
Традиционные структурные макромодели бесполезны для целей симуляции политики, поскольку такие модели не принимают в расчет в явной форме ожидания экономических агентов.
Симс:
В моделях Комиссии идентификация достигается за счет произвольного объявления некоторых переменных экзогенными. Однако в мире агентов, поведение которых зависит от решения некоторых вперед-смотрящих межвременных оптимизационных моделей, никакая из переменных не может считаться экзогенной.
Кроме того, в теоретическую априорную модель может быть включено недостаточное количество переменных (и тогда возникает эффект пропущенных переменных) и недостаточное количество запаздываний.
Слайд 10Для преодоления указанных недостатков методологии Комиссии были предложены:
методология Лондонской Школы экономики
методология VAR (векторных авторегрессий).
Слайд 11Методология LSE (Sargan, Hendry)
Акценты смещаются с методов оценивания (априорно заданной модели)
Строится достаточно широкая базовая модель в виде векторной ADL в приведенной форме с достаточно большим количеством переменных и достаточно большим количеством запаздываний (если, конечно, это позволяют данные).
Эта модель редуцируется путем упрощения динамики (отбрасывания незначимых лагов) и уменьшения размерности (отбрасывания уравнений для тех переменных, для которых не отвергается гипотеза экзогенности).
Накладываются ограничения на матрицу, определяющую долговременное равновесие, и производится идентификация коинтегрирующих векторов.
Слайд 12Методология LSE
Это приводит к статистической модели для данных с возможным разделением
Если система идентифицируема точно, то на этом все заканчивается.
Если система сверхидентифицирована, то проверяется выполнение "лишних" ограничений.
Слайд 13Методология VAR (Sims)
Разделение изменений в монетарной политике на два
изменения, которые агенты экономики предвидят правильно;
изменения, которые являются неожиданными для агентов экономики.
Изменения первого типа должны производить нейтральные эффекты: пропорциональные изменения цен и других номинальных переменных и отсутствие влияния на реальные переменные.
Неожиданные изменения второго типа, напротив, могут отражаться и на реальных переменных.
В методологии Симса делается акцент на исследование откликов системы экономических показателей на неожиданные (шоковые) воздействия, которым подвергаются отдельные переменные.
Слайд 14 В основе методологии VAR (как и в основе
лежит общая структура вида:
ζ t – инновационная последовательность
i.i.d. случайных (k х 1)- векторов с нулевым математическим ожиданием.
В приведенной форме:
ut – инновационная последовательность
i.i.d. случайных (k х 1)- векторов с нулевым математическим ожиданием и ковариационной матрицей Σ .
Слайд 15Простая VAR(1) для двух рядов (k = 2, p = 1)
Вычисляя эти изменения последовательно для значений s = 0, 1, … , получаем функции откликов на шоки инноваций.
На сколько изменяются значения при изменении инновации
или на одно стандартное отклонение?
Слайд 17При этом,
Корни уравнения
лежат за пределами единичного круга, так что
рассматриваемая VAR
Слайд 18Поэтому можно записать:
Тем самым, мы имеем возможность построения функций откликов
обеих
Слайд 19Однако:
Из-за того, что общем случае
Из-за перекрестной коррелированности инноваций в приведенной форме, невозможно полностью изолировать шок для u1t от шока для u2t , т.е.,
Нельзя произвольно изменять значение u1t , сохраняя при этом значения неизменными.
Слайд 20“Фундаментальные” инновации
Для преодоления указанного затруднения предполагают, что система изменяется благодаря
Обычно предполагается, что все они имеют единичные дисперсии, так что – i.i.d. с нулевым математическим ожиданием и единичной ковариационной матрицей Ik .
При этом предполагается, что инновации являются линейными комбинациями фундаментальных инноваций, так что
Слайд 21 В примере с двумерной VAR(1):
Поскольку
,
Изменение u1t на одно стандартное отклонение складывается из изменений и , которые, в свою очередь, вызывают одновременное изменение u2t .
Слайд 22 Импульсные функции отклика (impulse response function – IRF )
С экономической точки зрения, первоочередной интерес представляют реакции значений на единичные импульсные изменения отдельных фундаментальных инноваций при фиксированных значениях всех остальных фундаментальных инноваций во все моменты времени.
Именно на построение таких импульсных функций отклика нацелены алгоритмы, реализуемые в пакетах статистических программ.
Слайд 24Отсюда:
Для нахождения четырех неизвестных d1 , d2 , d3
Следовательно, матрицу D идентифицировать невозможно,
если не накладывать априорных ограничений на ее структуру.
Слайд 25упорядочивание инноваций в системе.
Пусть фундаментальная инновация воздействует
Тогда фундаментальная инновация воздействует только на u2t , а фундаментальная инновация воздействует и на u1t и на u2t .
Предложение Симса:
Пример двумерной VAR(1)
Слайд 27
Тогда
Обозначим
Умножим обе части VAR(1) на матрицу A :
Получаем структурную модель
в которой
Представим:
Слайд 28Пусть в приведенной VAR(1) ковариационная матрица ошибок имеет вид
так что
Тогда
Слайд 31Резюме:
При первом упорядочении инноваций:
При втором упорядочении инноваций:
В обоих случаях выбранная
Слайд 32 Рекурсивная система (первое упорядочение: Y1 ? Y2
В первое уравнение с текущим значением входит только одна переменная y1t , т.е.,
y1t объясняется только запаздывающими значениями переменных y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят обе переменные y1t и y2t , т.е. ,
y2t объясняется с помощью y1t и yt – 1 , yt – 2 , . . . ,
Такой порядок вхождения переменных интерпретируется как последовательное включение переменных в порядке возрастания их эндогенности, так что последней в систему включается наиболее эндогенная переменная.
Слайд 33Сравним функции отклика переменных y1t и y2t на импульсный шок фундаментальной
При первом упорядочении:
Пусть в момент t = 1 имеет место шок фундаментальной инновации для переменной y1t (в первом уравнении рекурсивной системы), так что
а не изменяется ни при каком t
Вернемся к двумерной VAR(1)
Слайд 34При этом мы получаем измененную реализацию
для которой
Для простоты, пусть . Тогда при t =1
а при t =2
Слайд 35Таким образом, мы получили следующие значения функций импульсного отклика на единичный
Слайд 36При втором упорядочении
Получаются следующие значения функций импульсного отклика
на единичный шок
Принимая различный порядок последовательного вхождения
переменных, мы получили и различное поведение функций
импульсного отклика.
Слайд 39Проблема: В примере функции импульсного отклика
Будем считать теперь эти параметры неизвестными и использовать для построения функций отклика их оценки, построенные по смоделированным реализациям длины 100.
Слайд 45Доверительные интервалы для (отдельных! ) значений импульсных откликов:
При первом упорядочении Y1
При втором упорядочении Y2 ?Y1:
Слайд 46Замечание
Столь существенное различие в поведении функций импульсного отклика при альтернативных упорядочениях
В сгенерированных данных эта корреляция равна -0.628, а для остатков от оцененной VAR она равна -0.634.
Слайд 47В общем случае предполагают, что структурная модель VAR имеет вид
т.е.
где
Соответственно, в приведенной форме
k -мерная VAR(p)
Слайд 48Приведенная форма:
Структурная форма:
Здесь
Приведенную форму оцениваем OLS, получаем оценки матриц
. Но по этим оценкам не всегда удается восстановить структурную форму, т.к. не известны матрицы A и B.
Слайд 49Проблема идентификации структурных уравнений по приведенной форме
В рассматриваемой ситуации
Оценив
Замена на приводит к оценочному уравнению для A и B:
Слайд 50Матрица симметрична, и поэтому достаточно оценить
Общее количество неизвестных элементов в матрицах и равно .
Поэтому идентификация возможна лишь при наложении на матрицы и достаточного количества ограничений.
Слайд 51Разложение Холецкого (Cholesky factorization)
Методология Симса, которую мы применили выше, фактически основана
Всякую положительно полуопределенную матрицу можно представить в виде произведения , где – верхняя треугольная матрица с положительными диагональными элементами, причем такая матрица единственна.
Обозначая , запишем указанное представление в виде:
Здесь D – нижняя треугольная матрица с положительными диагональными элементами.
Слайд 53Приравняем:
Тогда
(Нижняя треугольная матрица имеет обратную, которая также является нижней треугольной)
Слайд 54Резюме
Если наложить на матрицы A и B ограничения:
A – нижняя треугольная
B – диагональная матрица с положительными диагональными элементами,
то уравнение
имеет единственное решение, т.е. имеет место точная идентифицируемость матриц A и B .
Диагональные элементы bjj матрицы B можно рассматривать как с.к.о. инновации в i-м уравнении структуры, а форма матрицы A соответствует рекурсивной системе .
Слайд 55Рекурсивная система
В первое уравнение с текущим значением входит только одна
y1t объясняется только запаздывающими значениями переменных y1t , y2t , . . . , ykt .
Во второе уравнение с текущими значениями входят только переменные y1t и y2t , т.е. ,
y2t объясняется с помощью y1t и yt – 1 , yt – 2 , . . . ,
. . .
В последнее, k-е уравнение с текущими значениями входят все переменные y1t , y2t , . . . , ykt , т.е.,
ykt объясняется с помощью y2t , . . . , yk-1,t и yt – 1 , yt – 2 , . . .
Такой порядок вхождения переменных интерпретируется как последовательное включение переменных в порядке возрастания их эндогенности, так что последней в систему включается наиболее эндогенная переменная.
При выбранной нормализации (единицы на диагонали матрицы ),
y1t – “наименее эндогенная” переменная,
ykt – “наиболее эндогенная” переменная
Слайд 56Вернемся к k -мерной VAR(p)
Приведенная форма:
Запишем ее в виде:
Если все корни
лежат за пределами единичного круга, то VAR стабильна, и можно записать:
Слайд 57k -мерная VAR(p)
Это есть векторное MA-представление k -мерного ряда y1t
основанное на инновационной последовательности ut .
Если для некоторого k-мерного случайного вектора выполнено соотношение
то
Слайд 58и если
так что матрица D является корнем из матрицы и имеет левую нижне-треугольную форму:
Ее элементы легко вычисляются рекуррентным образом
по элементам ковариационной матрицы .
Слайд 59Матрицу D можно представить в виде
При этом, представление
разложением Холецкого матрицы .
Слайд 60 Разложение Холецкого (Cholesky factorization)
P* – левая нижне-треугольная матрица с единицами на диагонали,
B – диагональная матрица.
Мы уже фактически использовали такую факторизацию ранее для матрицы
где
Слайд 61 Функция импульсных откликов
Теперь
и произвести подстановку .
В результате получаем разложение
основанное на инновационной последовательности
Элемент матрицы с индексом ij равен изменению i-ой переменной в момент времени t+h в ответ на единичное изменение шока j-ой переменной в момент времени t при сохранении неизменными всех остальных шоков во все моменты времени.
Слайд 62Декомпозиция (разложение) дисперсии ошибок прогнозов (variance decomposition)
Прогноз по VAR на
Ошибка прогноза по VAR на один шаг вперед:
Слайд 63Ошибка прогноза по VAR на один шаг вперед:
Рассмотрим матрицу
Ee математическое ожидание
на диагонали которой находятся значения дисперсий ошибок
прогнозов на один шаг вперед рядов y1 и y2 .
Слайд 65Дисперсия ошибки прогноза на один шаг вперед ряда y1
Дисперсия ошибки прогноза
Слайд 66Дисперсия ошибки прогноза на один шаг вперед ряда y1
Дисперсия ошибки прогноза
Получили декомпозиции дисперсий ошибок прогноза
– разложение каждой из них на две компоненты.
Что представляют собой эти компоненты?
Слайд 67
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– дисперсия ошибки прогноза на один шаг вперед ряда y1
Слайд 68 – составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– составляющая ошибки прогноза на один шаг вперед ряда y1,
обусловленная фундаментальной инновацией
– дисперсия ошибки прогноза на один шаг вперед ряда y1
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
Слайд 69 – дисперсия ошибки прогноза на один шаг вперед ряда y1
–
ряда y1, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
Слайд 70 – дисперсия ошибки прогноза на один шаг вперед ряда y2
–
ряда y2, обусловленная фундаментальной инновацией
– составляющая дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
Слайд 72– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1,
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y1, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
– доля дисперсии ошибки прогноза на один шаг вперед
ряда y2, обусловленная фундаментальной инновацией
Слайд 73Ошибка прогноза по VAR на h шагов вперед вычисляется по формуле:
где
Декомпозиция дисперсии ошибок прогнозов
Слайд 74Ошибка прогноза по VAR на h шагов вперед вычисляется по формуле:
Вкдад
Декомпозиция дисперсии ошибок прогнозов
Слайд 75 Декомпозиция дисперсии ошибок прогнозов
Обычно результат такой декомпозиции представляется как
В пакетах программ статистического анализа предлагаются также графики, показывающие динамику изменений каждой такой доли с изменением h, h =1, 2, . . .
Слайд 80Оценивание SVAR в EViews
При первом упорядочении
или
И, так как
и А – нижняя треугольная матрица с единицами на диагонали,
а B – диагональная матрица, то
Слайд 82В рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки в
Статистическая модель:
Слайд 83y1=c(1)*y1(-1)+c(2)*y2(-1)
y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1)
Результаты оценивания:
Coefficient Std. Error t-Statistic Prob. ---------------------------------------------------------
C(1) 0.610340 0.041871 14.57663 0.0000
C(2) 0.497220 0.047645 10.43600 0.0000
C(3) -0.988495 0.122953 -8.039596 0.0000
C(4) 0.810082 0.090567 8.944557 0.0000
C(5) 1.156414 0.084061 13.75689 0.0000
Слайд 84EViews:
Оценивание матриц A и B структурной формы
Создав объект VAR и
можно получить в рамках этого объекта и оценки указанных матриц.
Для этого заказываем: Proc ? Estimate Structural Factorization
В открывшемся окне указываем форму связи между ошибками в приведенной VAR и фундаментальными инновациями, соответствующую выбранному упорядочению в схеме Холецкого.
Слайд 86
Model: Ae = Bu where E[uu']=I
Restriction Type: short-run text form
@e1 =
@e2 = C(2)*@e1 + C(3)*@u2
where
@e1 represents Y1 residual
@e2 represents Y2 residuals
Coefficient
C(2) -0.997582
C(1) 0.962944
C(3) 1.143882
Estimated A matrix:
1.000000 0.000000
0.997582 1.000000
Estimated B matrix:
0.962944 0.000000
0.000000 1.143882
Результаты оценивания матриц A и B
Слайд 87Замечания
Принимая различные порядки последовательного вхождения переменных, мы получаем и различное поведение
В рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки в разных уравнениях являются взаимно некоррелированными случайными величинами. Это означает, что соответствующую систему одновременных уравнений можно оценивать, используя обычный метод наименьших квадратов (OLS).
Слайд 88Пример. В модели двумерной VAR переменная y1t может представлять объем производства (output),
Упорядочение y1t ? y2t соответствует схеме
В этой схеме шоки в объеме производства оказывают немедленное воздействие и на объем производства и на деньги, тогда как шоки в деньгах оказывают немедленное воздействие только на деньги.
Такое упорядочение соответствует представлению, согласно которому денежная политика имеет только запаздывающее влияние на объем производства.
u1t
u2t
Слайд 89Пример (продолжение)
Упорядочение y2t ? y1t соответствует схеме
В этой схеме шоки
Это соответствует представлению о том, что деньги поставляются центральным банком, а объем производства становится известным центральному банку лишь с опозданием. Поэтому деньги не могут немедленно реагировать на шоки в объеме производства.
u2t
u1t
























































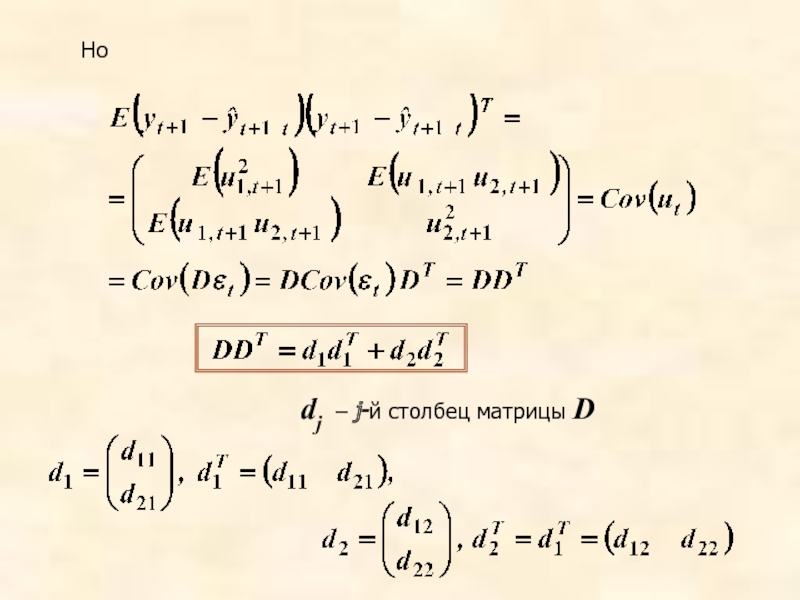















![Model: Ae = Bu where E[uu']=I Restriction Type: short-run text form @e1 = C(1)*@u1 @e2 = C(2)*@e1 +](/img/tmb/4/341220/43c116a68909fe6570a6d8ef0715c03e-800x.jpg)