- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эконометрика-II. Оценивание SVAR в EViews 6 презентация
Содержание
- 1. Эконометрика-II. Оценивание SVAR в EViews 6
- 2. Оценивание SVAR в EViews 6 При первом
- 3. Таким образом, при первом упорядочении SVAR (структурная VAR) принимает вид:
- 4. В рекурсивной структуре, полученной с использованием изложенного
- 5. y1=c(1)*y1(-1)+c(2)*y2(-1) y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1) Результаты оценивания: Coefficient Std. Error t-Statistic Prob. --------------------------------------------------------- C(1) 0.610340 0.041871 14.57663 0.0000
- 6. EViews 6: Оценивание матриц A и
- 7. Warning! Обозначения ошибок другие! Но матрицы A и B те же!
- 8. Model: Ae = Bu where E[uu']=I
- 9. Замечания Принимая различные порядки последовательного вхождения переменных,
- 10. Пример. В модели двумерной VAR переменная y1t
- 11. Пример (продолжение) Упорядочение y2t ➔ y1t
- 12. Методология VAR: Эмпирические исследования
- 13. Sims (1980): сравнение динамики экономики США в
- 14. Упорядочение y1t ➔ y2t ➔ y3t
- 15. Декомпозиции дисперсий ошибок прогнозов трех переменных на
- 16. Влияние процентной ставки VAR с 4
- 17. Упорядочение: R ➔ M1 ➔ P
- 18. Leeper, Sims, Zha (1996): модели VAR с
- 19. Отклики переменных LP и LY
- 20. Отклики переменной LM2
- 21. Декомпозиция дисперсий переменной LM2
- 22. В то же время, деньги играют более
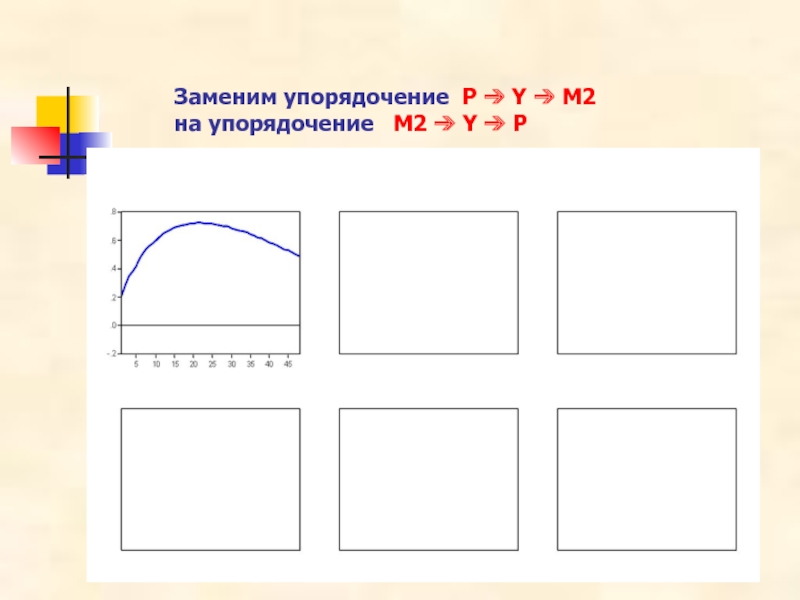
- 23. Заменим упорядочение P ➔ Y ➔ M2
- 25. Графики очень похожи! Почему все так
- 26. Причинность по Грейнджеру, функции импульсного отклика и
- 27. Если набор
- 28. Leeper, Sims, Zha (1996): модель VAR с
- 29. Декомпозиция дисперсий ошибок прогнозов
- 30. Функции импульсных откликов И здесь влияние инноваций
- 31. Нестабильные VAR Законно ли использование инструментария, предназначенного
- 32. Филлипс [Phillips (1995)] При наличии единичных
- 33. Филлипс [Phillips (1995)] Если имеет место коинтегрированность
- 34. Смоделирована VAR(1):
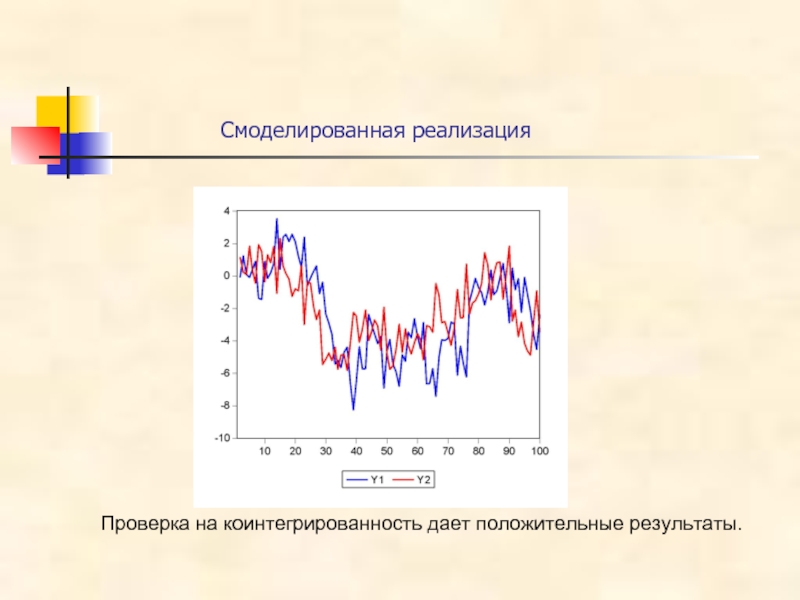
- 35. Смоделированная реализация Проверка на коинтегрированность дает положительные результаты.
- 36. Оцененная UVAR(1)
- 37. Отклики для оцененной UVAR
- 38. Поведение последовательностей откликов в модели, использованной в
- 39. Отклики приращений
- 40. Пример с тремя рядами DGP:
- 41. Смоделированная реализация
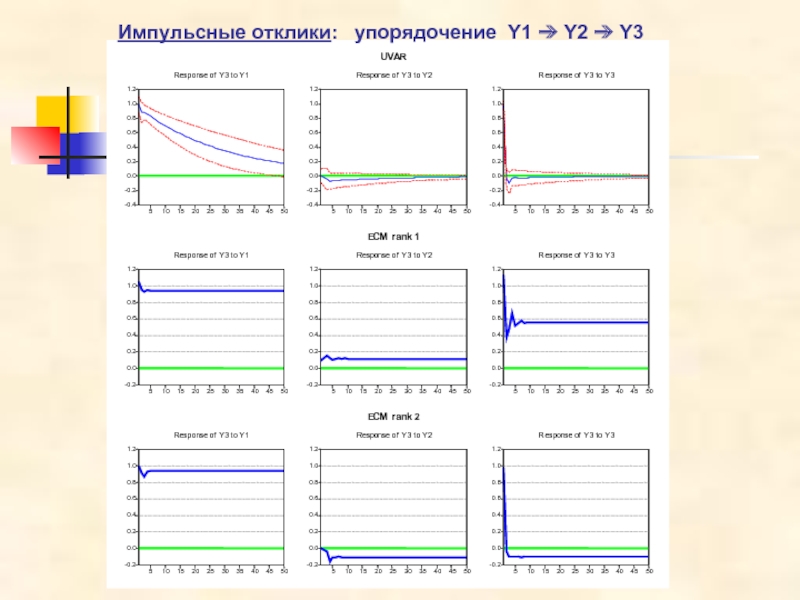
- 42. Импульсные отклики: упорядочение Y1 ➔ Y2 ➔ Y3
- 43. Выводы Использование при оценивании ECM различных предположений
Слайд 2Оценивание SVAR в EViews 6
При первом упорядочении
или
И, так как
и А – нижняя треугольная матрица с единицами на диагонали,
а B – диагональная матрица, то
Слайд 4В рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки в
Статистическая модель:
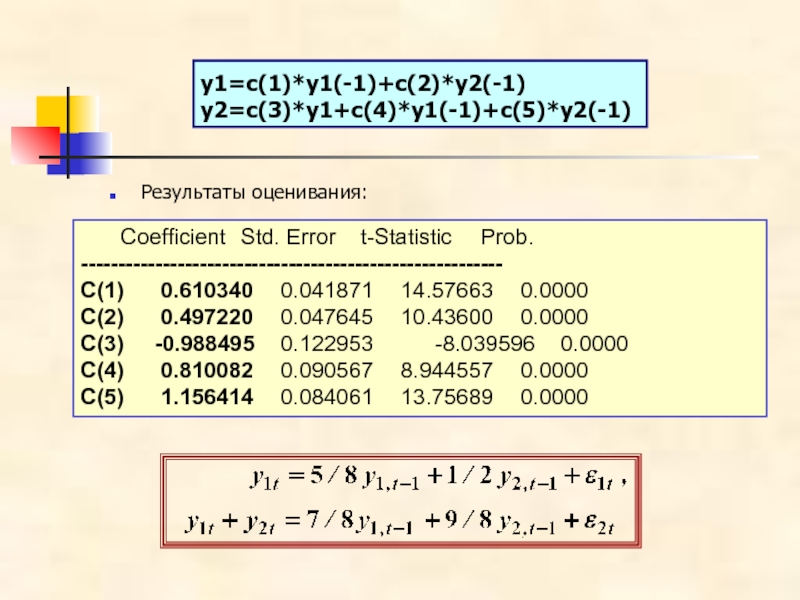
Слайд 5y1=c(1)*y1(-1)+c(2)*y2(-1)
y2=c(3)*y1+c(4)*y1(-1)+c(5)*y2(-1)
Результаты оценивания:
Coefficient Std. Error t-Statistic Prob. ---------------------------------------------------------
C(1) 0.610340 0.041871 14.57663 0.0000
C(2) 0.497220 0.047645 10.43600 0.0000
C(3) -0.988495 0.122953 -8.039596 0.0000
C(4) 0.810082 0.090567 8.944557 0.0000
C(5) 1.156414 0.084061 13.75689 0.0000
Слайд 6EViews 6:
Оценивание матриц A и B структурной формы
Создав объект VAR
можно получить в рамках этого объекта и оценки указанных матриц.
Для этого заказываем: Proc ➔ Estimate Structural Factorization
В открывшемся окне указываем форму связи между ошибками в приведенной VAR и фундаментальными инновациями, соответствующую выбранному упорядочению в схеме Холецкого.
Слайд 8
Model: Ae = Bu where E[uu']=I
Restriction Type: short-run text form
@e1 =
@e2 = C(2)*@e1 + C(3)*@u2
where
@e1 represents Y1 residual
@e2 represents Y2 residuals
Coefficient
C(2) -0.997582
C(1) 0.962944
C(3) 1.143882
Estimated A matrix:
1.000000 0.000000
0.997582 1.000000
Estimated B matrix:
0.962944 0.000000
0.000000 1.143882
Результаты оценивания матриц A и B
Слайд 9Замечания
Принимая различные порядки последовательного вхождения переменных, мы получаем и различное поведение
В рекурсивной структуре, полученной с использованием изложенного метода, случайные ошибки в разных уравнениях являются взаимно некоррелированными случайными величинами. Это означает, что соответствующую систему одновременных уравнений можно оценивать, используя обычный метод наименьших квадратов (OLS).
Слайд 10Пример. В модели двумерной VAR переменная y1t может представлять объем производства (output),
Упорядочение y1t ➔ y2t соответствует схеме
В этой схеме шоки в объеме производства оказывают немедленное воздействие и на объем производства и на деньги, тогда как шоки в деньгах оказывают немедленное воздействие только на деньги.
Такое упорядочение соответствует представлению, согласно которому денежная политика имеет только запаздывающее влияние на объем производства.
u1t
u2t
Слайд 11Пример (продолжение)
Упорядочение y2t ➔ y1t соответствует схеме
В этой схеме шоки
Это соответствует представлению о том, что деньги поставляются центральным банком, а объем производства становится известным центральному банку лишь с опозданием. Поэтому деньги не могут немедленно реагировать на шоки в объеме производства.
u2t
u1t
Слайд 13Sims (1980): сравнение динамики экономики США в период между двумя мировыми
VAR с 3 переменными (месячные данные)
M1 – денежный агрегат M1 (сезонно скорректированная);
IP – индекс промышленного производства (сезонно скорректированная);
P – индекс оптовых цен (сезонно скорректированная).
Все переменные брались в логарифмах, в правые части уравнений включались константы и по 12 лагов каждой переменной.
Упорядочение: Денежная масса ➔ Объем производства ➔ Цены
Соответственно, y1t ➔ y2t ➔ y3t , где
y1t = M1 , y2t = IP , y3t = P .
Слайд 14Упорядочение y1t ➔ y2t ➔ y3t соответствует схеме:
M1 – “
Схема влияния фундаментальных инноваций
u2t
u3t
u1t
Денежная масса ➔ Объем производства ➔ Цены
Слайд 15Декомпозиции дисперсий ошибок прогнозов трех переменных на 48 месяцев вперед
Для
Инновации M1 объясняют значительную часть дисперсии IP и существенную часть дисперсии P.
Все это вполне в духе монетаризма, если понимать монетаризм как точку зрения, согласно которой денежная политика играет центральную роль в цикле деловой активности, а динамика денежной массы является хорошим показателем денежной политики.
Денежная масса ➔ Объем производства ➔ Цены
Слайд 16Влияние процентной ставки
VAR с 4 переменными –
добавляется Rt –
Упорядочение: R ➔ M1 ➔ P ➔ IP
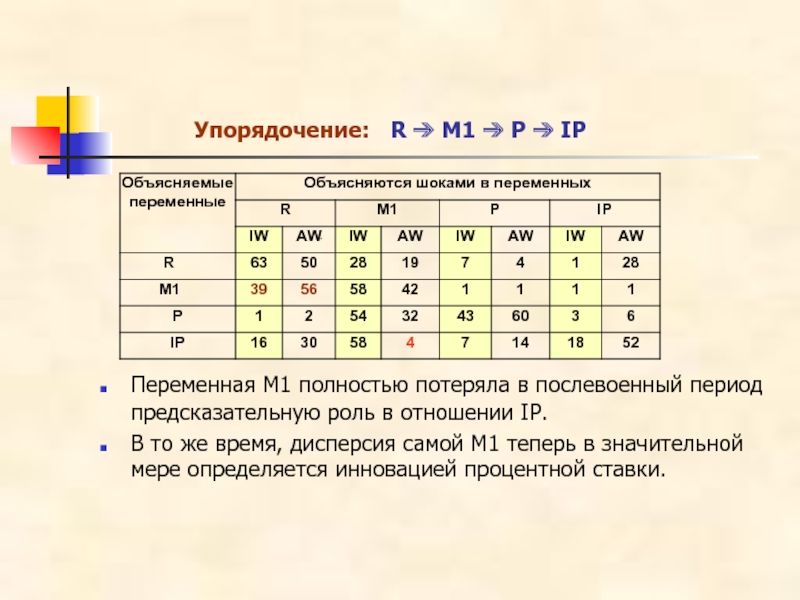
Слайд 17Упорядочение: R ➔ M1 ➔ P ➔ IP
Переменная M1 полностью
В то же время, дисперсия самой M1 теперь в значительной мере определяется инновацией процентной ставки.
Слайд 18Leeper, Sims, Zha (1996): модели VAR с 3, 4 и 5 переменными
VAR с 3 переменными
Переменные:
Оценивание на периоде 1960:01 – 1996:03 ( T=435)
В уравнения включались константы и по 6 лагов каждой переменной.
Упорядочение: P ➔ Y ➔ M2
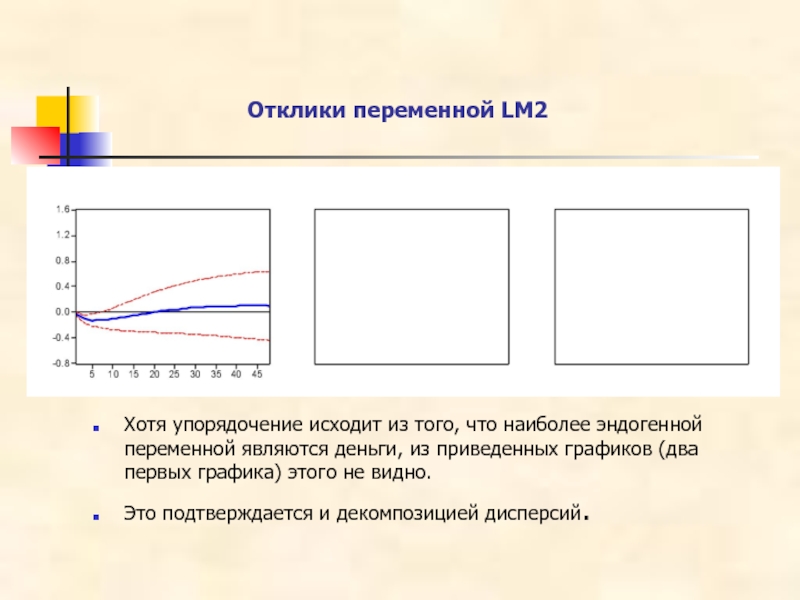
Слайд 20Отклики переменной LM2
Xотя упорядочение исходит из того, что наиболее эндогенной переменной
Это подтверждается и декомпозицией дисперсий.
Слайд 21Декомпозиция дисперсий переменной LM2
Цены и объем производства играют весьма ограниченную роль
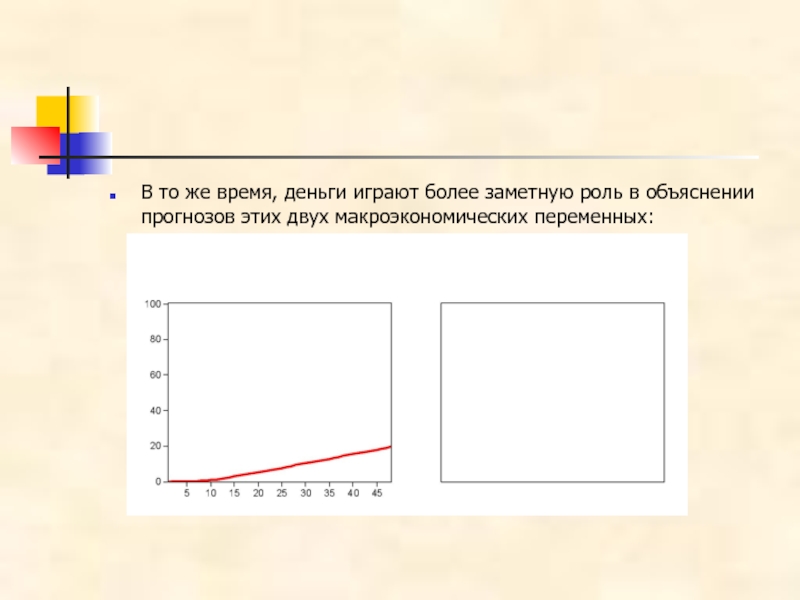
Слайд 22В то же время, деньги играют более заметную роль в объяснении
Слайд 25Графики очень похожи!
Почему все так похоже?
Получается, что порядок вхождения
Но это возможно только если инновации в приведенной VAR не коррелированы между собой.
Корреляции между остатками на сей раз имеют вид:
Во всяком случае, в обоих вариантах:
эндогенность M2 незаметна ;
M2 играет более заметную роль в объяснении дисперсий прогнозов реального GDP.
Слайд 26Причинность по Грейнджеру, функции импульсного отклика и декомпозиция дисперсий.
Тесты на наличие
В то же время, функции импульсного отклика и декомпозиции дисперсий позволяют проследить динамику влияния шоковых воздействий на будущие значения переменных.
Свойство отсутствия G-причинности между переменными двух групп является исключительным свойством двух подмножеств переменных данного процесса. В то же время, декомпозиция дисперсий ошибок прогнозов не единственна: она зависит от матрицы, приводящей к фундаментальным инновациям.
Слайд 27
Если набор переменных в составе yt
и переменные второй группы не являются Грейнджер-причиной для переменных первой группы, то это
вовсе не означает, что доли дисперсий ошибок прогнозов переменных группы 1, соответствующие инновациям в уравнениях для переменных второй группы, равны нулю.
Последнее может иметь место только если отсутствует перекрестная коррелированность инноваций в уравнениях для переменных группы 1 с инновациями в уравнениях для переменных группы 2.
Если же это условие нарушено, то доли дисперсий ошибок прогнозов переменных группы 1, соответствующие инновациям в уравнениях для переменных группы 2 отличны от нуля.
Слайд 28Leeper, Sims, Zha (1996):
модель VAR с 3 переменными
Переменные:
Упорядочение: P ➔
При оценивании на периоде 1974:01 – 1980:03 ( T=75 наблюдений) ранее было выявлено наличие G-причинной связи в направлении от LY к LM2.
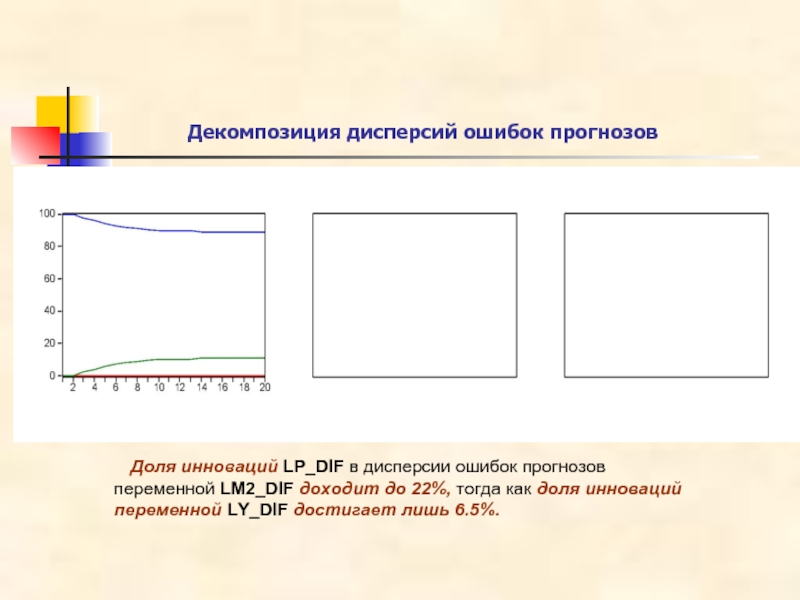
Слайд 29Декомпозиция дисперсий ошибок прогнозов
Доля инноваций LP_DIF в дисперсии
переменной LM2_DIF доходит до 22%, тогда как доля инноваций
переменной LY_DIF достигает лишь 6.5%.
Слайд 30Функции импульсных откликов
И здесь влияние инноваций LY_DIF на LM2_DIF значимо только
Слайд 31Нестабильные VAR
Законно ли использование инструментария, предназначенного для анализа стабильных моделей VAR,
Слайд 32Филлипс [Phillips (1995)]
При наличии единичных корней или корней, близких к
Импульсные отклики, полученные на основании оцененной приведенной VAR без ограничений, в долговременном плане сходятся в пределе не к истинным откликам, а к некоторым случайным величинам.
Предельное распределение не является нормальным и несимметрично.
Предсказания на основании нестационарной VAR без ограничений не сходятся к оптимальным прогнозам (по крайней мере, на больших горизонтах прогнозов), а дисперсия оптимального прогноза, как правило занижается.
Слайд 33Филлипс [Phillips (1995)]
Если имеет место коинтегрированность рядов, образующих VAR, и оценивается
Построенные по оцененной модели импульсные отклики и декомпозиции дисперсий прогнозов состоятельны, а прогнозы асимптотически оптимальны.
Правда, для этого надо или
правильно специфицировать ранг коинтеграции или
получить для него состоятельную оценку.
Слайд 34 Смоделирована VAR(1):
В этой модели один из корней характеристического уравнения равен
Слайд 36 Оцененная UVAR(1)
Соответствующая приведенная форма:
DGP:
Разница между оценками, полученными по моделям UVAR и ECM, весьма мала.
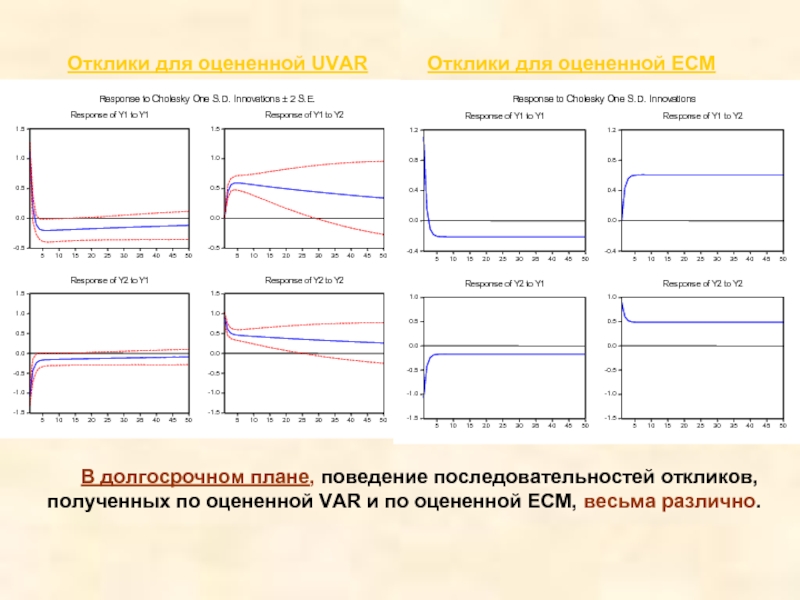
Слайд 37Отклики для оцененной UVAR
Отклики для оцененной ECM
В долгосрочном плане, поведение последовательностей откликов,
полученных по оцененной VAR и по оцененной ECM, весьма различно.
Слайд 38Поведение последовательностей откликов в модели, использованной в DGP
Из графиков видно,
поведение функций отклика
при использовании UVAR не соответствует
поведению функций отклика в DGP,
тогда как поведение функций отклика
при использовании ECM соответствует поведению функций отклика в DGP.
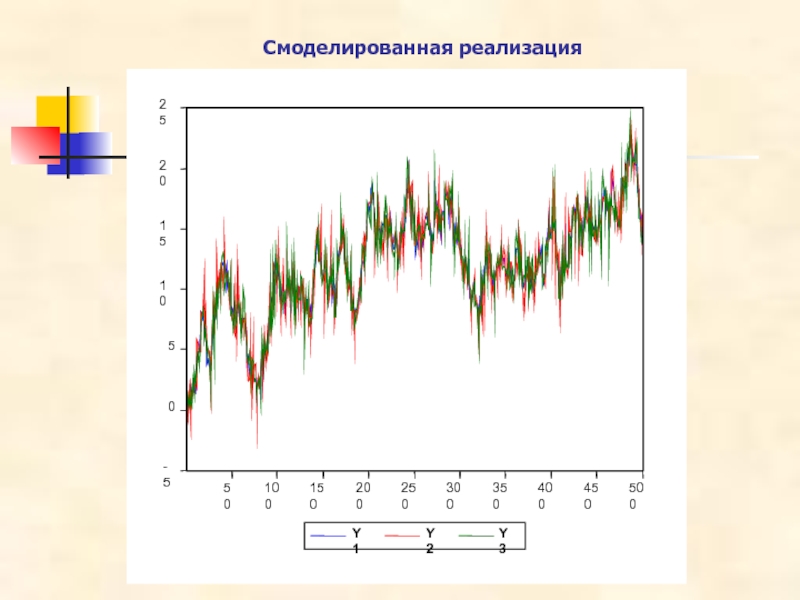
Слайд 40Пример с тремя рядами
DGP:
где
Получаемые I(1) ряды коинтегрированы, ранг коинтеграции равен 2.
Слайд 43Выводы
Использование при оценивании ECM различных предположений о ранге коинтеграции приводит к
Это весьма затрудняет интерпретацию результатов VAR анализа при обращении к данным экономической статистики.






![Model: Ae = Bu where E[uu']=I Restriction Type: short-run text form @e1 = C(1)*@u1 @e2 = C(2)*@e1 +](/img/tmb/2/167825/fa4657c1f1b265be367cb94b7f4a7cb6-800x.jpg)


















![Филлипс [Phillips (1995)] При наличии единичных корней или корней, близких к единице: Импульсные отклики, полученные](/img/tmb/2/167825/77584fe10b703e7d9d802af7fee1ceb5-800x.jpg)
![Филлипс [Phillips (1995)]Если имеет место коинтегрированность рядов, образующих VAR, и оценивается модель VAR, учитывающая ограничения,](/img/tmb/2/167825/8d7aac7b611cd243b4f2096583e8b82e-800x.jpg)