- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цилиндр, конус и шар презентация
Содержание
- 1. Цилиндр, конус и шар
- 2. Понятие цилиндра О О1
- 3. Тело, ограниченное цилиндрической поверхностью и
- 4. Сечения цилиндра : Если секущая плоскость проходит
- 5. Площадь поверхности цилиндра: За площадь боковой поверхности
- 6. Пусть дана плоскость
- 7. Проведем прямую, перпендикулярно этой плоскости, а
- 8. Выберем на прямой произвольную точку и
- 9. Поверхность, состоящая из всех таких отрезков,
- 10. Поверхность, состоящая из всех таких отрезков,
- 11. Поверхность, состоящая из всех таких отрезков, называется конической поверхностью
- 12. Тело, состоящее из конической поверхности и круга, граница которого принадлежит конической поверхности, называется круговым конусом
- 13. Конус в переводе с греческого «konos» означает
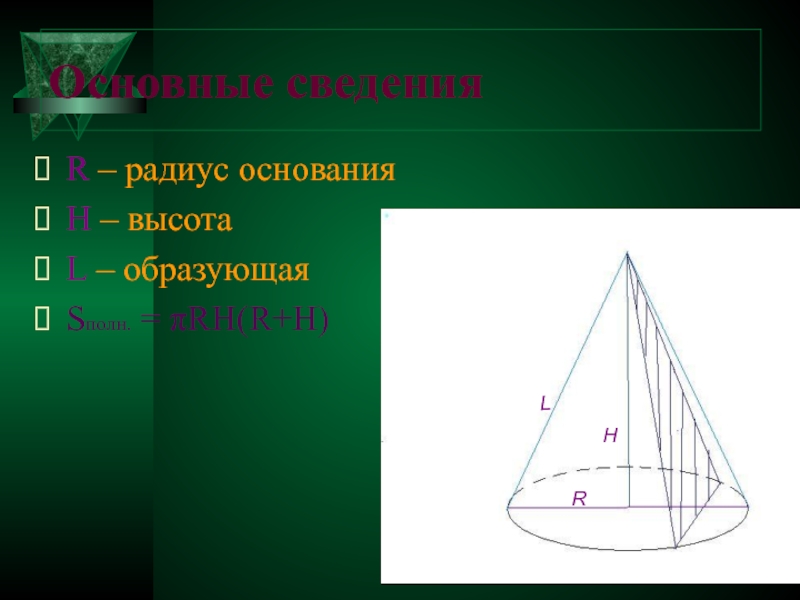
- 14. Основные сведения R – радиус основания H
- 15. Практическое применение конические детали в машинах и
- 16. Практическое применение
- 17. Практическое применение
- 18. Практическое применение
- 19. СФЕРА. Сферой называется поверхность, состоящая из всех
- 20. Теорема Радиус сферы, проведенный в точку касания
- 21. Волгина Таня Юдина Катя Жижелева Маша Учитель: Широкова О.В. НАД ПРОЕКТОМ РАБОТАЛИ:
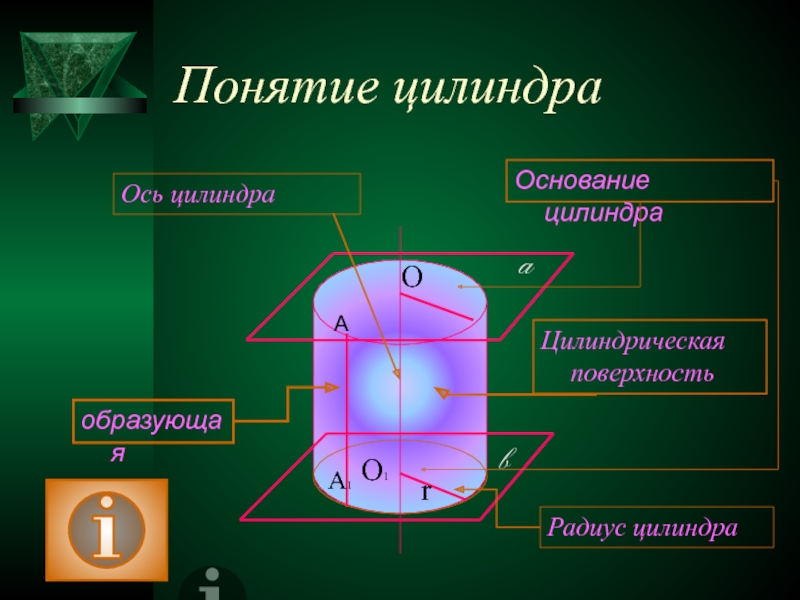
Слайд 2Понятие цилиндра
О
О1
a
b
А
А1
образующая
Основание цилиндра
Цилиндрическая поверхность
Ось цилиндра
r
Радиус цилиндра
Слайд 3
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами, называется цилиндром.
Цилиндрическая
Длина образующей – высота цилиндра.
Цилиндр можно получить вращением прямоугольника вокруг одной из его сторон
Слайд 4Сечения цилиндра :
Если секущая плоскость проходит через ось цилиндра, то сечение
Такое сечение называется осевым.
Сечение является кругом, если секущая плоскость перпендикулярна к оси цилиндра
Слайд 5Площадь поверхности цилиндра:
За площадь боковой поверхности цилиндра принимается площадь её развёртки
Площадь
S = 2Пr(r + h)
Sбок = 2пrh
Слайд 7
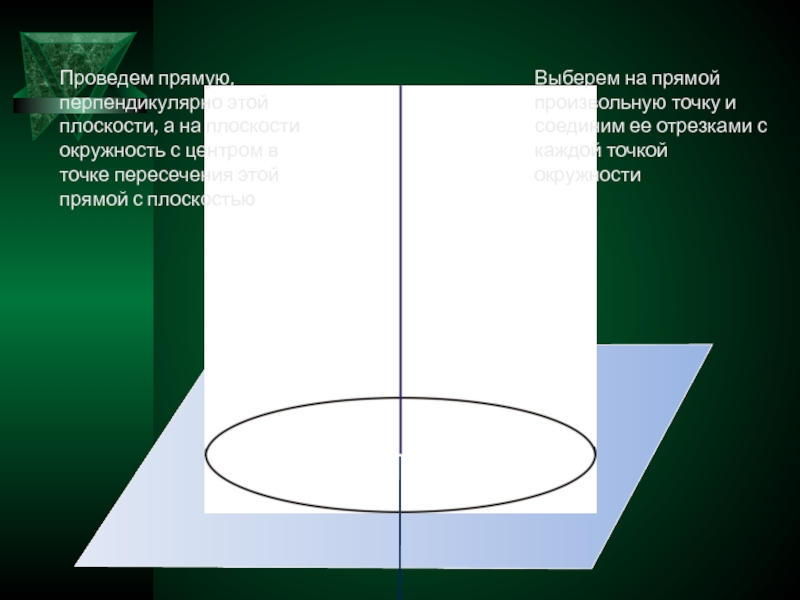
Проведем прямую, перпендикулярно этой плоскости, а на плоскости окружность с центром
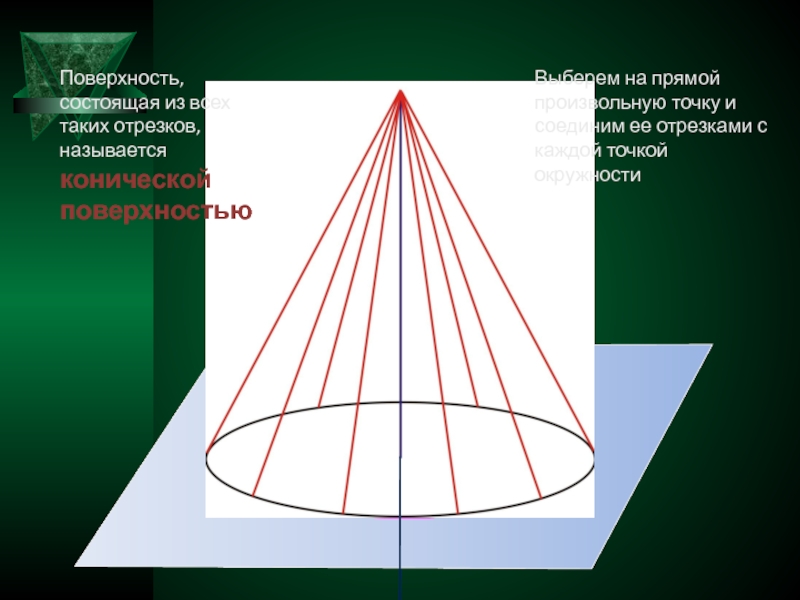
Выберем на прямой произвольную точку и соединим ее отрезками с каждой точкой окружности
Слайд 8
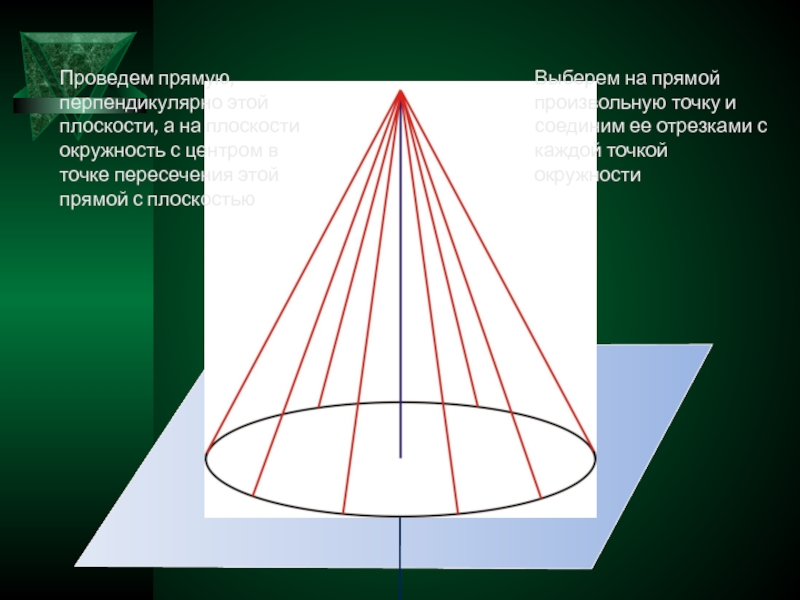
Выберем на прямой произвольную точку и соединим ее отрезками с каждой
Проведем прямую, перпендикулярно этой плоскости, а на плоскости окружность с центром в точке пересечения этой прямой с плоскостью
Слайд 9
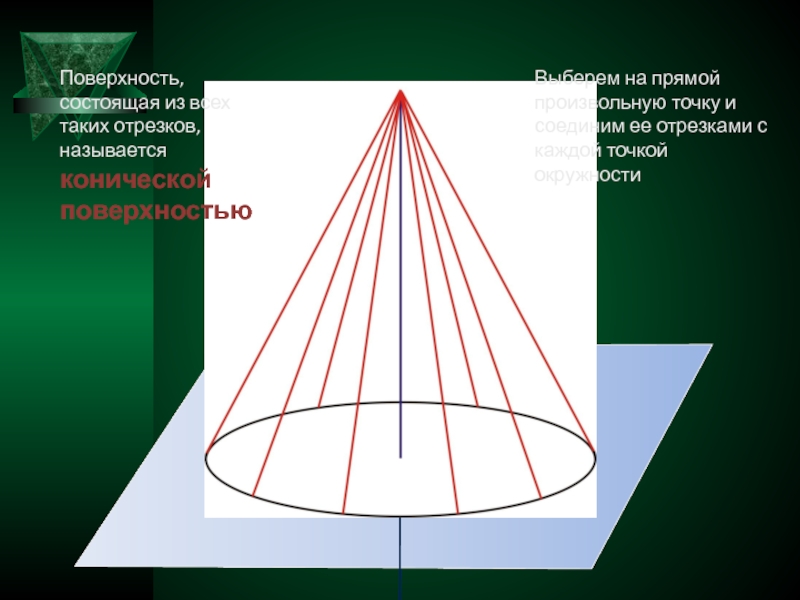
Поверхность, состоящая из всех таких отрезков, называется
конической поверхностью
Выберем на прямой
Слайд 10
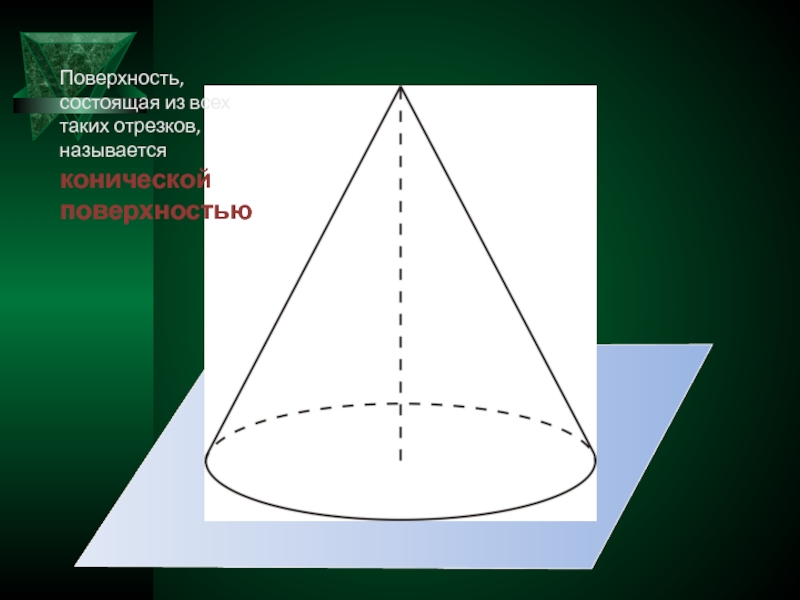
Поверхность, состоящая из всех таких отрезков, называется
конической поверхностью
Выберем на прямой
Слайд 12Тело, состоящее из конической поверхности и круга, граница которого принадлежит конической
Слайд 13Конус в переводе с греческого «konos» означает «сосновая шишка». С конусом
Много сделала для геометрии школа Платона (428-348 гг. до н.э.). Платон был учеником Сократа (470-399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: «Пусть сюда не входит никто, не знающий геометрии». Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260-170 гг. до н.э.) – учеником Евклида (III в. До н.э.), который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Слайд 15Практическое применение
конические детали в машинах и механизмах;
в автомобилях, танках, бронетранспортёрах –
носовая часть самолётов и ракет.
Слайд 19СФЕРА.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном
Слайд 20Теорема
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к
Теорема
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.