- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Триггеры и колебания в биологии презентация
Содержание
- 1. Триггеры и колебания в биологии
- 3. Бифуркационный анализ Поиск качественных изменений в решении
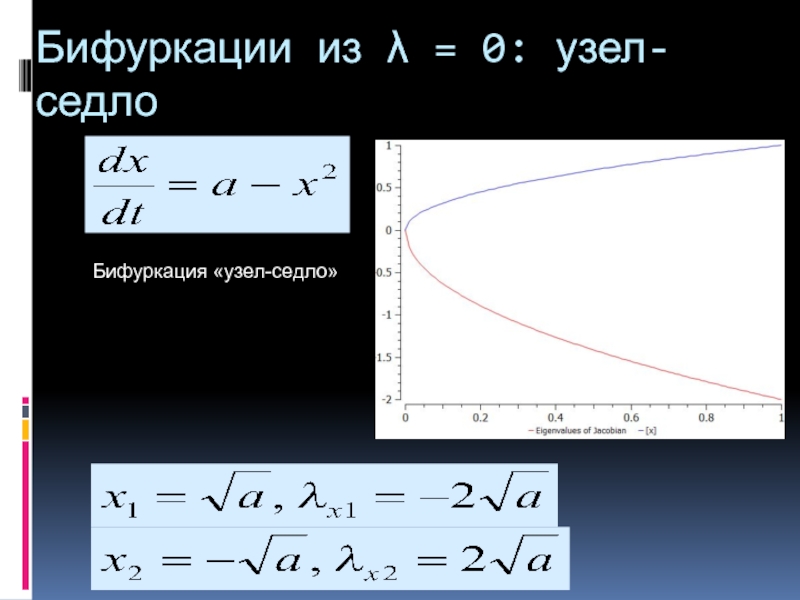
- 4. Бифуркация «узел-седло» Бифуркации из λ = 0: узел-седло
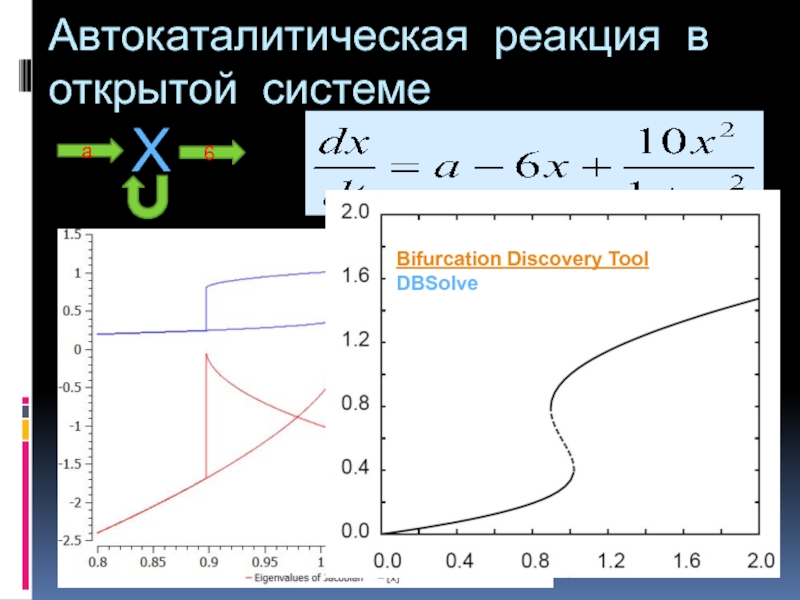
- 5. Автокаталитическая реакция в открытой системе Bifurcation Discovery Tool DBSolve X a 6
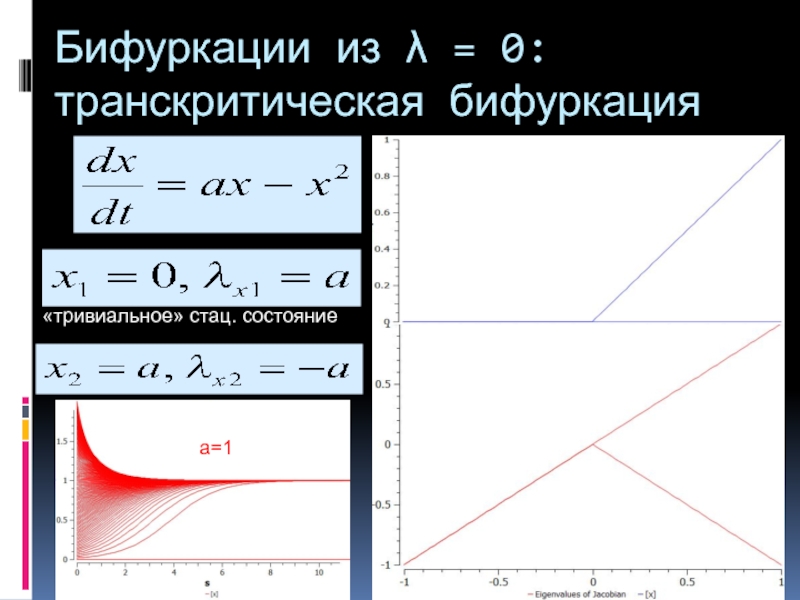
- 7. Бифуркации из λ = 0: транскритическая бифуркация «тривиальное» стац. состояние a=1
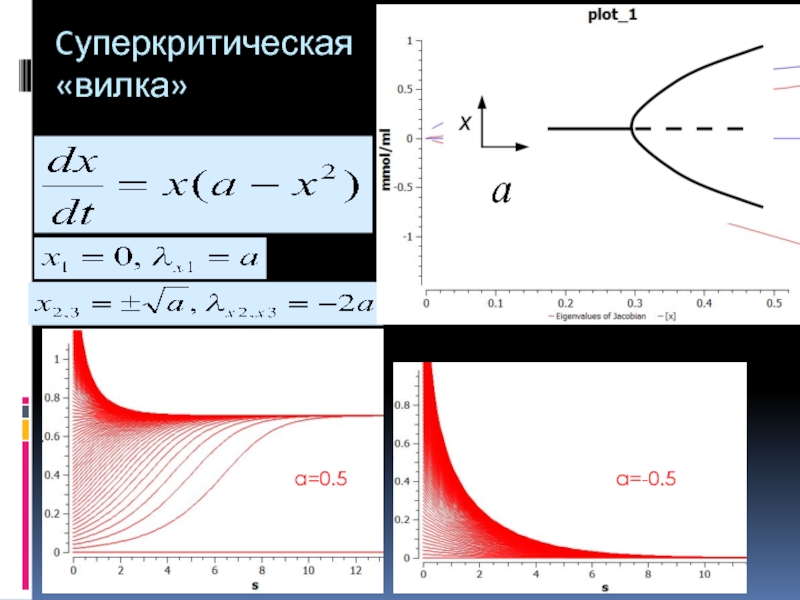
- 8. Cуперкритическая «вилка» a=0.5 a=-0.5
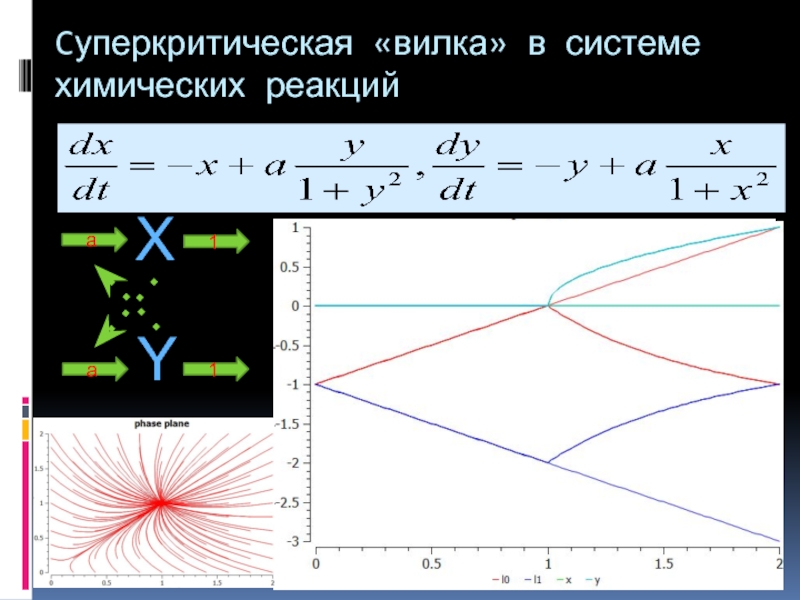
- 9. Cуперкритическая «вилка» в системе химических реакций X a 1 Y 1 a
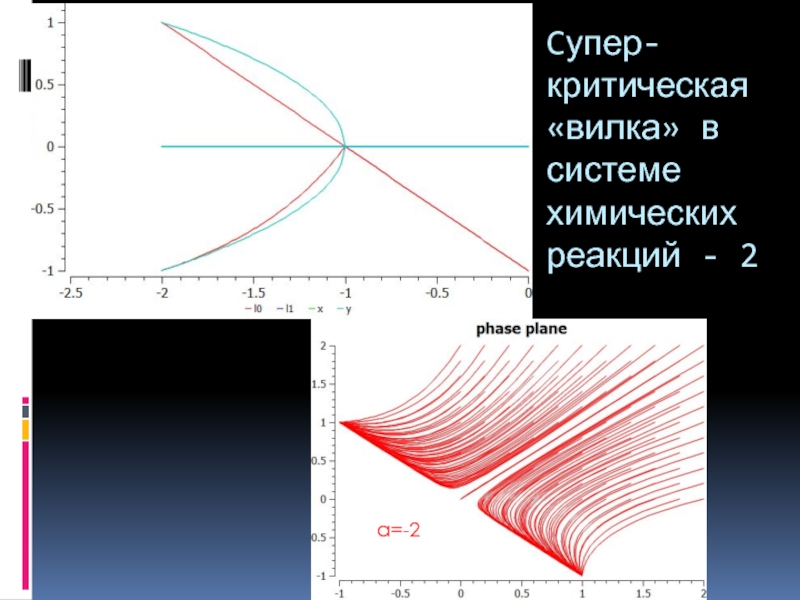
- 10. Cупер-критическая «вилка» в системе химических реакций - 2 a=-2
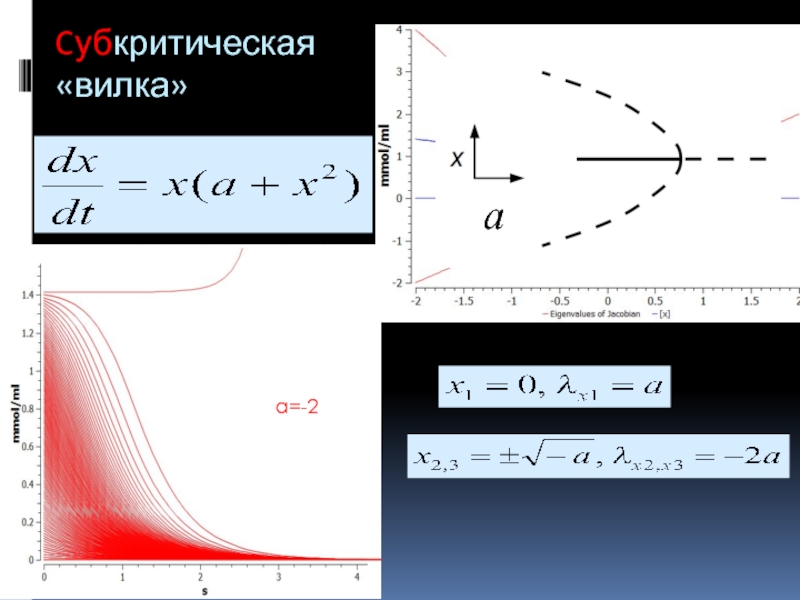
- 11. Cубкритическая «вилка» a=-2
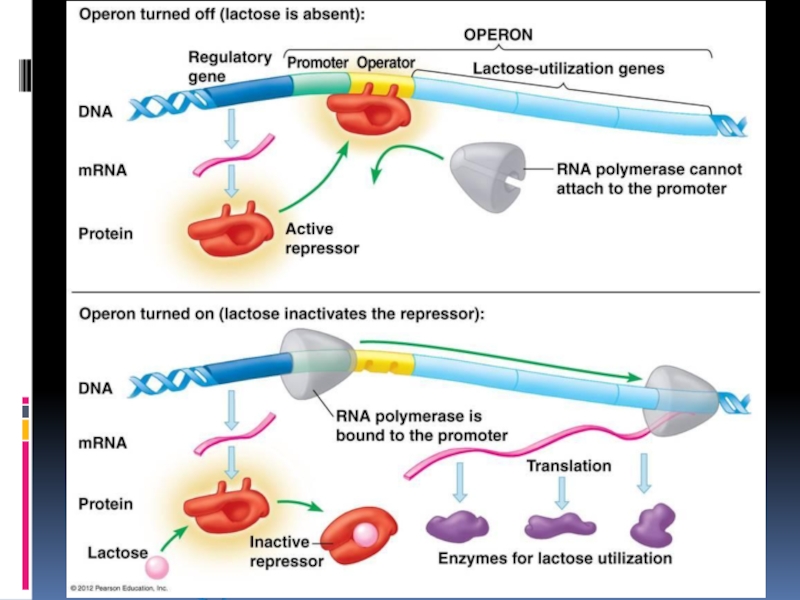
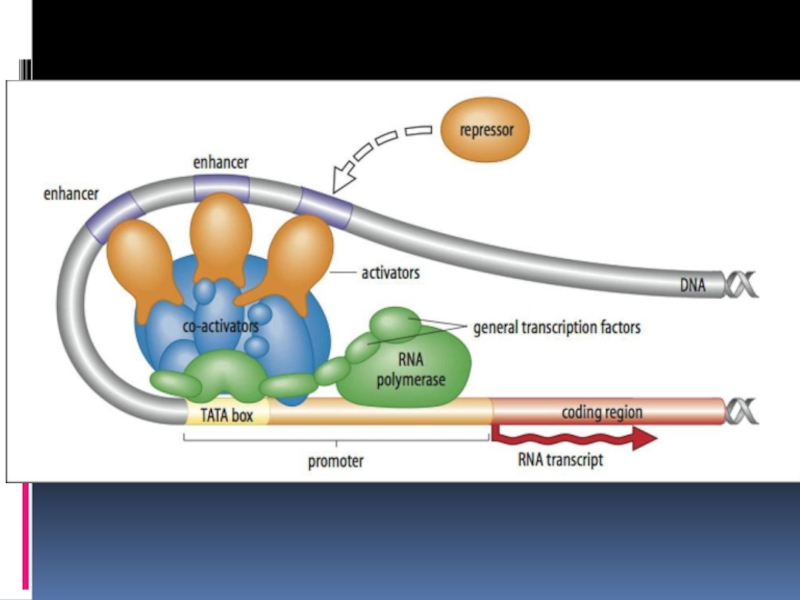
- 12. Регуляция экспрессии генов Прокариоты: оперон Эукариоты: все уровни
- 14. E. Coli trp Repressor
- 16. Messenger RNA (M) Operon-polymerase
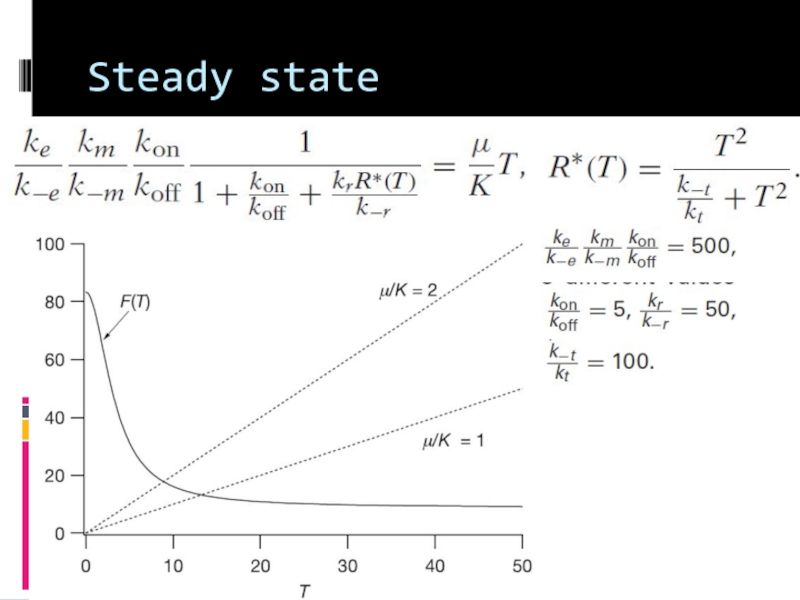
- 17. Steady state
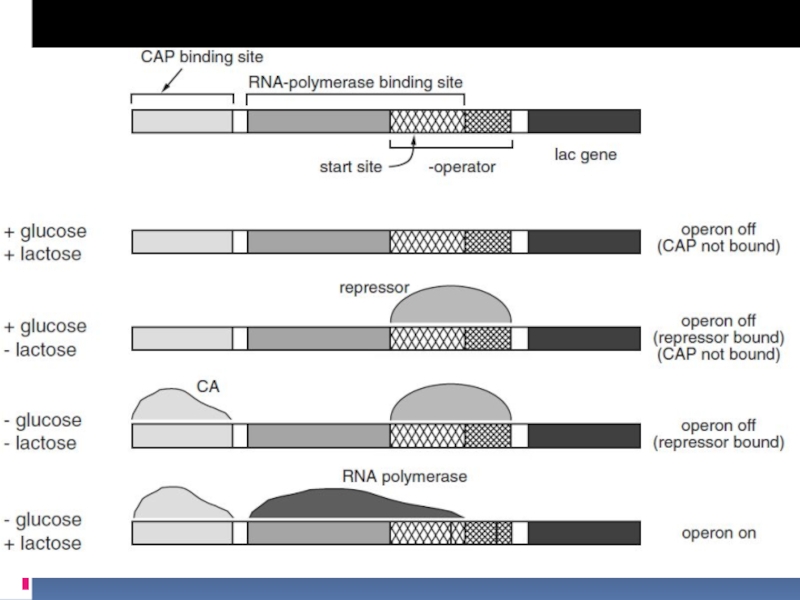
- 18. E. Coli lac operon lactose permease
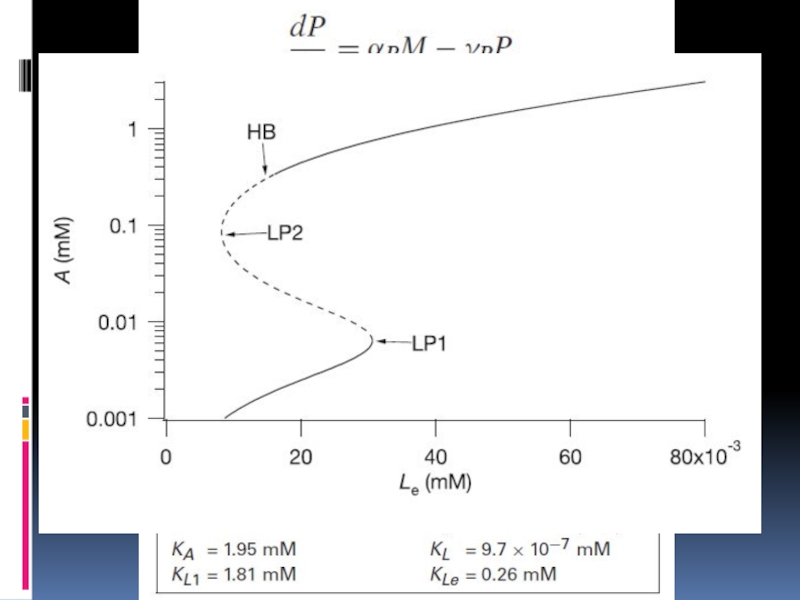
- 21. Allolactose (А), lactose (L), permease (P)
- 23. Триггер Жакоба-Мано
- 24. Триггер Жакоба-Мано: γ=1, L=4 m
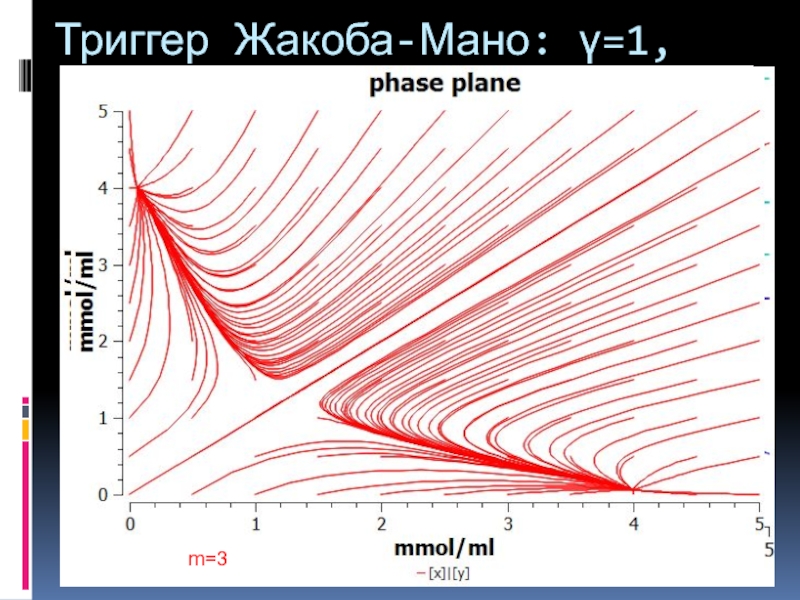
- 25. Триггер Жакоба-Мано: m=3, L=1.61 gamma
- 26. Предельный цикл О1. Предельным циклом векторного поля
- 27. Предельный цикл С каждой из сторон
- 28. Теорема Пуанкаре-Бендиксона О2. Предельное множество —это множество
- 29. Теорема Пуанкаре-Бендиксона
- 30. Критерий Бендиксона Если дивергенция векторного поля на
- 31. Бифуркации из пары комплексно-сопряженных λ:
- 32. Бифуркация Андронова-Хопфа суперкритическая бифуркация
- 33. Бифуркация Андронова-Хопфа субкритическая бифуркация с <
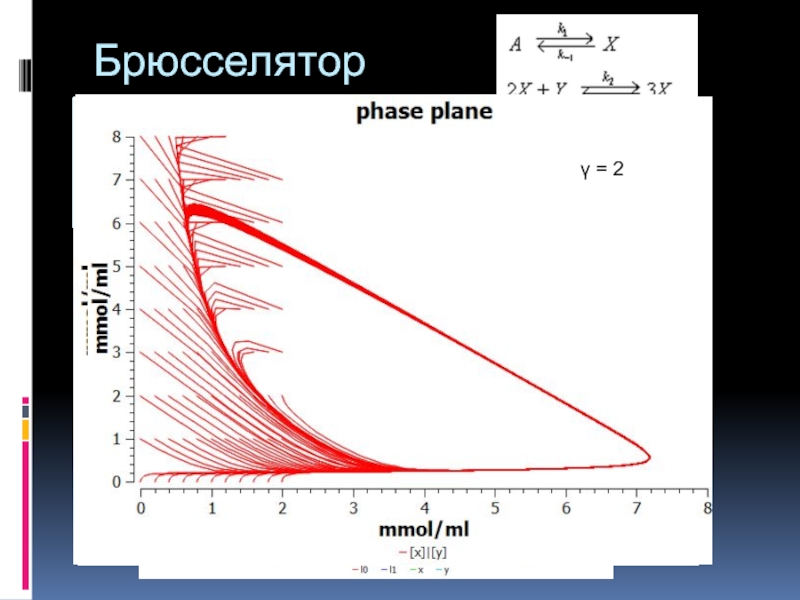
- 34. Брюсселятор
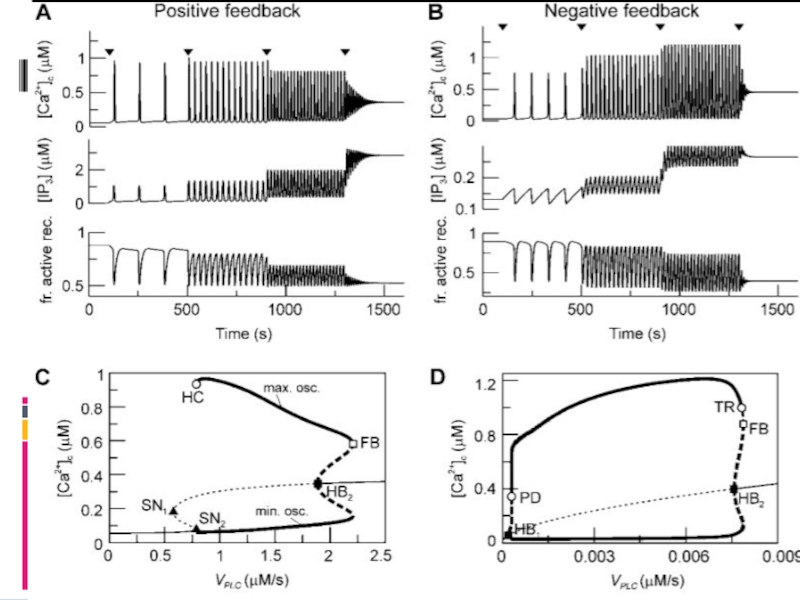
- 36. Я автокатализ автоингибирование Положительная обратная связь Отрицательная обратная связь Длинная обратная связь
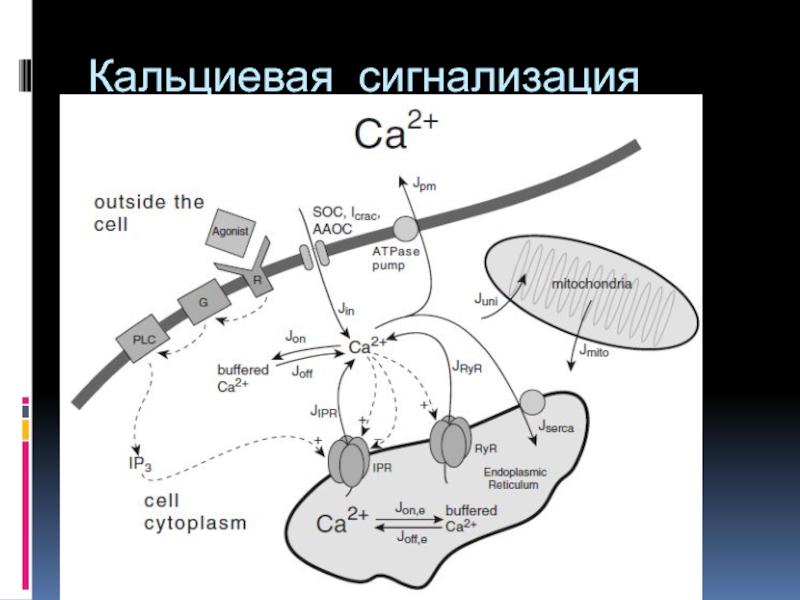
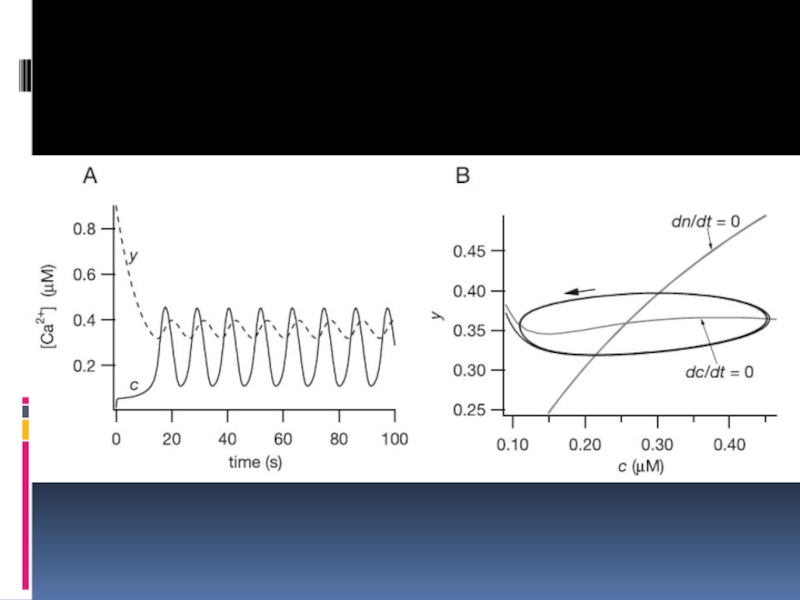
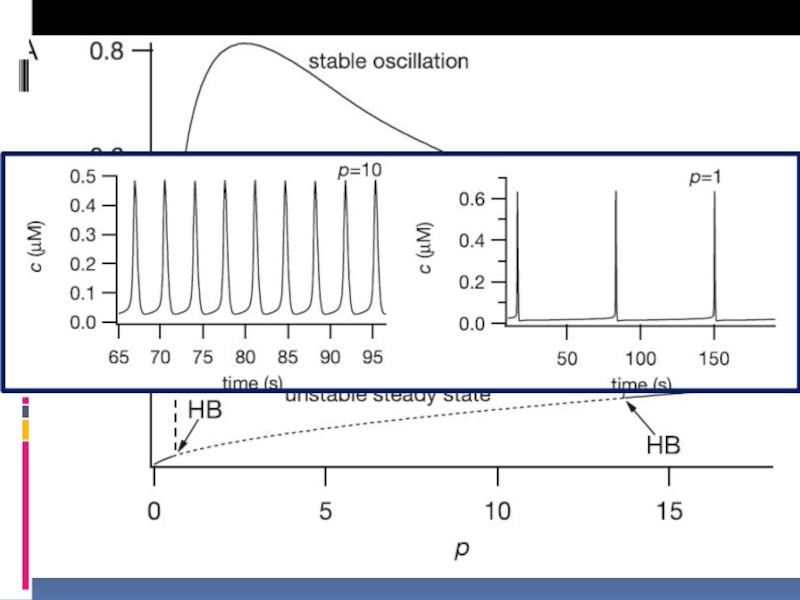
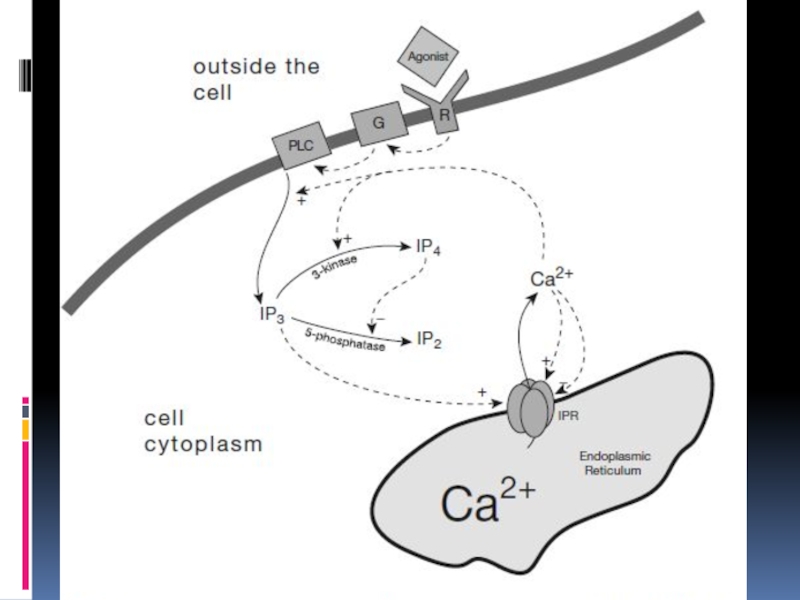
- 37. Кальциевая сигнализация
- 42. Открытая система
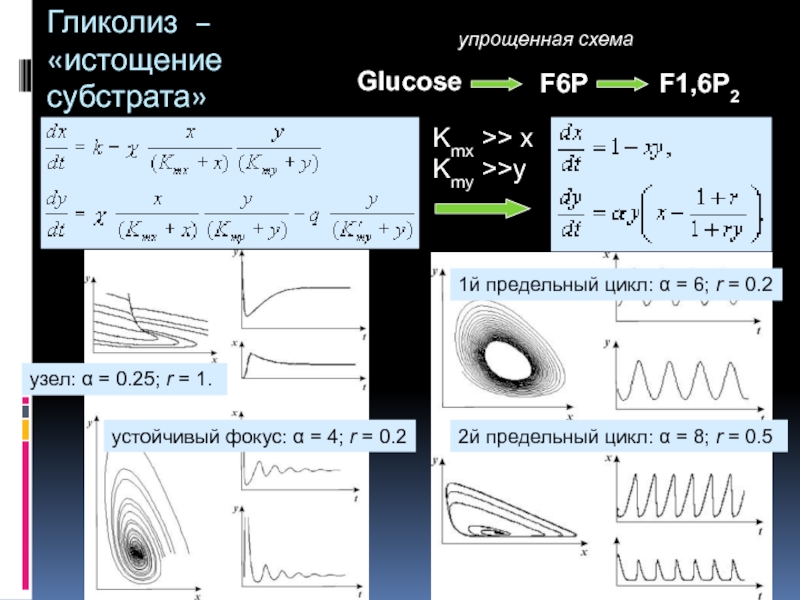
- 47. Гликолиз – «истощение субстрата» Glucose F6P F1,6P2
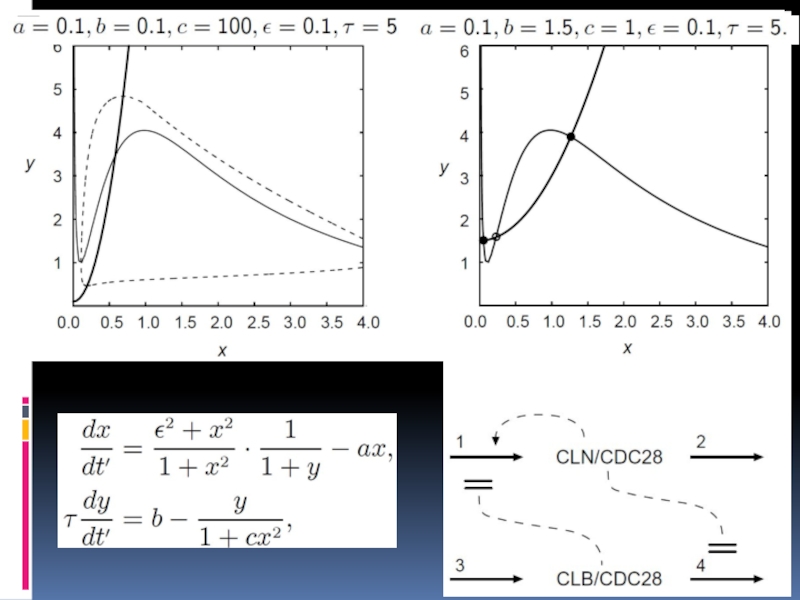
- 48. Циклины – «активатор-ингибитор»
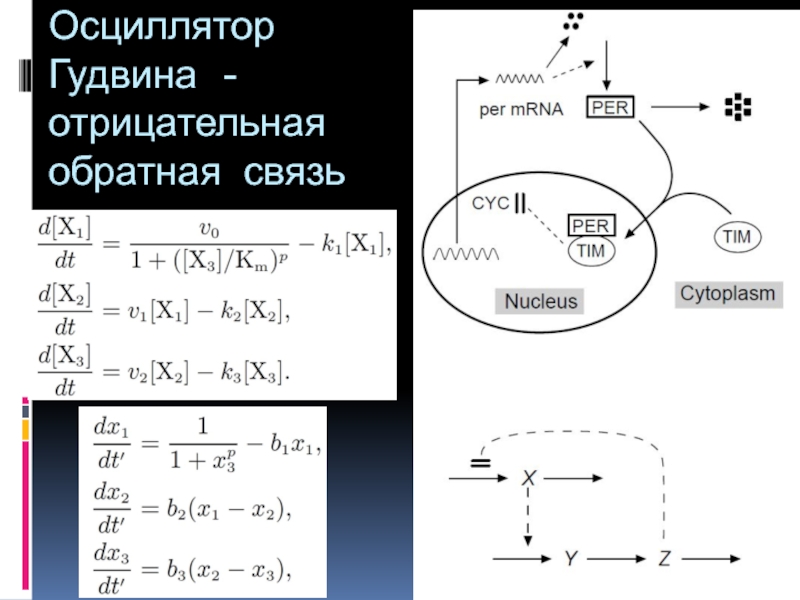
- 49. Осциллятор Гудвина - отрицательная обратная связь
- 50. Спасибо за внимание!
- 51. Предельный цикл Теорема 1. Пусть на фазовой плоскости существует
Бифуркационный анализ Поиск качественных изменений в решении системы дифференциальных уравнений при изменении параметров системы График зависимости стационарного состояния от бифуркационного параметра называется бифуркационной диаграммой Бифуркации стационых состояний: λ (real) λr =0
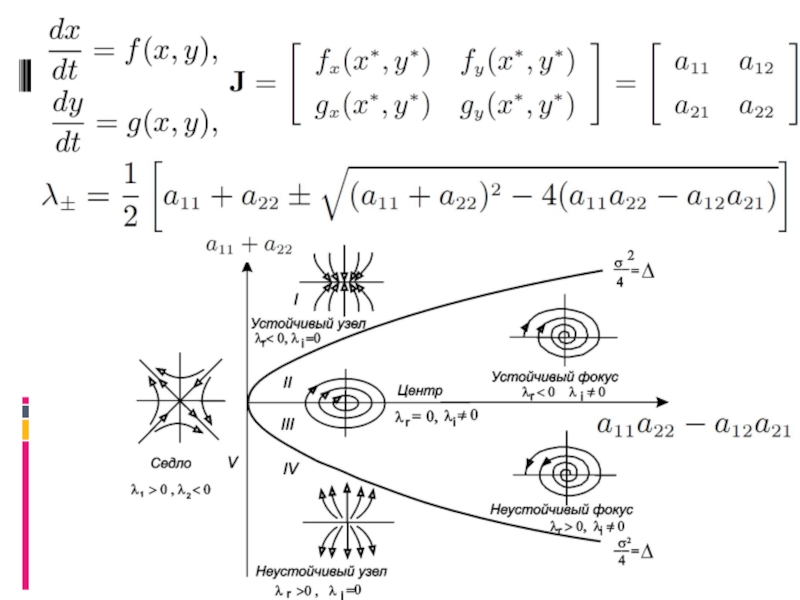
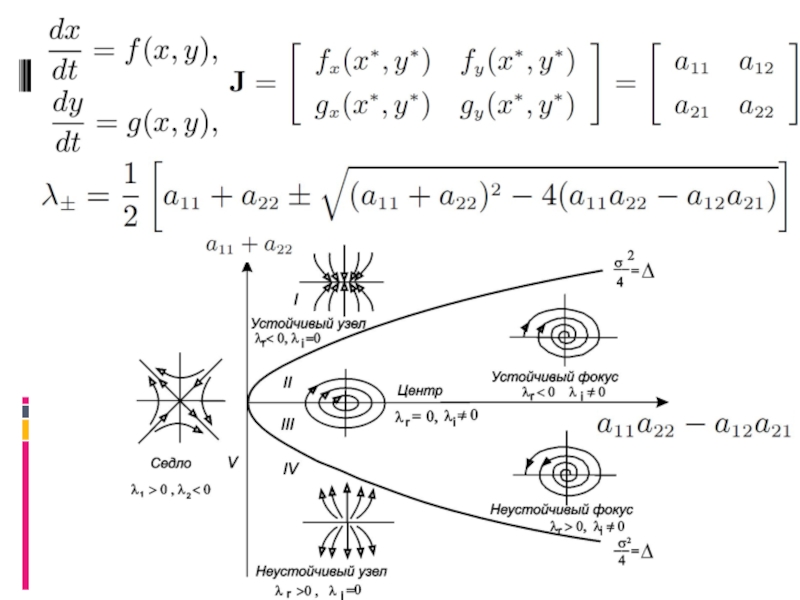
Слайд 3Бифуркационный анализ
Поиск качественных изменений в решении системы дифференциальных уравнений при изменении
параметров системы
График зависимости стационарного состояния от бифуркационного параметра называется бифуркационной диаграммой
Бифуркации стационых состояний:
λ (real) <0 -> λr =0 -> λr >0
График зависимости стационарного состояния от бифуркационного параметра называется бифуркационной диаграммой
Бифуркации стационых состояний:
λ (real) <0 -> λr =0 -> λr >0
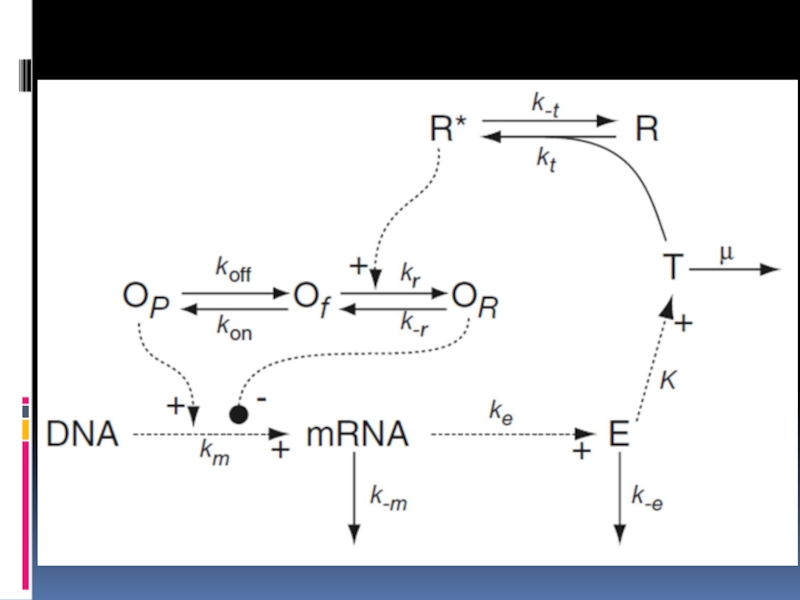
Слайд 16
Messenger RNA (M)
Operon-polymerase
Operon- repressor
oP + of + oR = 1
activated repressor
Enzyme
Trp
Слайд 18E. Coli lac operon
lactose
permease
β-galactosidase
thiogalactoside
transacetylase
расщепление
лактозы
транспорт
Лактозы в клетку
Слайд 21
Allolactose (А), lactose (L), permease (P)
β-galactosidase (B), mRNA (M), repressor (R)
Operon-repressor
(or), operon-producing (op)
Steady-state
Steady-state
Слайд 26Предельный цикл
О1. Предельным циклом векторного поля на фазовой плоскости называется замкнутая
(периодическая) траектория этого векторного поля, в окрестности которой нет других периодических траекторий.
Слайд 27Предельный цикл
С каждой из сторон предельный цикл является либо отталкивающим,
либо притягивающим. Если поведение с обеих сторон одинаково — цикл называется соответственно отталкивающим или притягивающим. Если же с одной стороны происходит притяжение, а с другой отталкивание — говорят о полуустойчивом цикле
Слайд 28Теорема Пуанкаре-Бендиксона
О2. Предельное множество —это множество состояний, к которым объект неограниченно
приближается при неограниченном возрастании (или убывании) времени.
Т1. Пусть задано C1-гладкое векторное поле на плоскости или в некоторой области плоскости, имеющее лишь конечное число особых точек. Тогда ω-предельное множество любой траектории — это либо (1) особая точка, либо (2) периодическая траектория, либо (3) полицикл (объединение особых точек и соединяющих их отрезков траекторий).
Т1. Пусть задано C1-гладкое векторное поле на плоскости или в некоторой области плоскости, имеющее лишь конечное число особых точек. Тогда ω-предельное множество любой траектории — это либо (1) особая точка, либо (2) периодическая траектория, либо (3) полицикл (объединение особых точек и соединяющих их отрезков траекторий).
Слайд 30Критерий Бендиксона
Если дивергенция векторного поля на плоскости знакопостоянна и отлична от
нуля в некоторой односвязной области, то отсутствуют замкнутые фазовые кривые этого поля, целиком лежащие в этой области.
Слайд 31
Бифуркации из пары комплексно-сопряженных λ: теорема Хопфа
Тогда в системе есть предельный
цикл в области a0, причем радиус цикла пропорционален и частота близка к ω0
Цикл стабильный если ν > 0 и цикл существует при а > а0, либо если ν < 0 и цикл существует при а < а0. В противном случае он нестабильный.
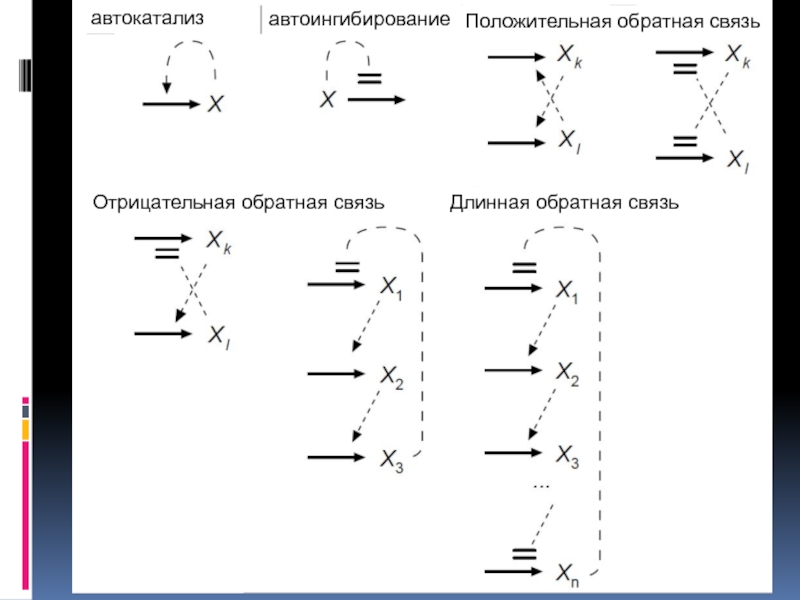
Слайд 36Я
автокатализ
автоингибирование
Положительная обратная связь
Отрицательная обратная связь
Длинная обратная связь
Слайд 47Гликолиз – «истощение субстрата»
Glucose
F6P
F1,6P2
упрощенная схема
Kmx >> x
Kmy >>y
узел: α = 0.25; r = 1.
устойчивый фокус:
α = 4; r = 0.2
1й предельный цикл: α = 6; r = 0.2
2й предельный цикл: α = 8; r = 0.5
Слайд 51Предельный цикл
Теорема 1. Пусть на фазовой плоскости существует область, из которой фазовые траектории
не выходят, и в которой нет положений равновесия (особых точек). Тогда в этой области обязательно существует предельный цикл, причем все остальные траектории обязательно наматываются на него.
Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл
Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл
