f(x1)= f(x2) > f(x3)
§ 17. Исследование поведения функции
Аналитические признаки монотонности функции
а) возрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1) b) убывающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)>f(x2); c) невозрастающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)≥f(x2); d) неубывающей на (a,b), если ∀x1, x2∈(a,b) при x1< x2 f(x1)≤f(x2).

![Теорема 17.1. (Достаточное условие строгой монотонности)Пусть y=f(x) непрерывна на [a,b] и дифференцируема на (a,b), тогда](/img/tmb/4/315256/3c07374a7e1a801f3a219c955158aaba-800x.jpg)
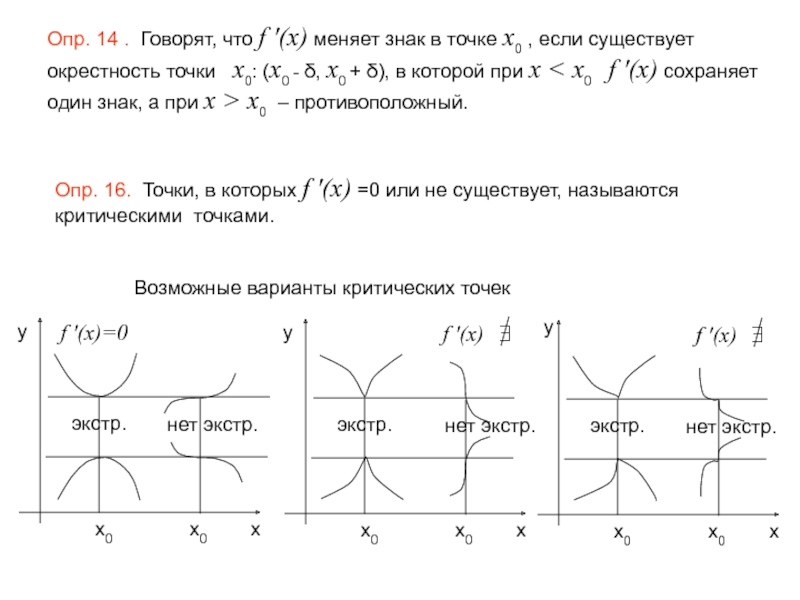

![Отыскание наибольшего и наименьшего значения функции на [a, b]Вспомним:Если ∀ x ∈ [a, b] выполняется](/img/tmb/4/315256/64a08d762b728017931d5806ffdf41fe-800x.jpg)
![Теорема 17.4. (Достаточное условие выпуклости и вогнутости кривой)Пусть y = f (x) непрерывна на [a,b],](/img/tmb/4/315256/acb0cd4cd00a1c7d021442d225fcd367-800x.jpg)






