- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Знакомый – незнакомый ряд презентация
Содержание
- 1. Знакомый – незнакомый ряд
- 2. Цель работы: показать красоту
- 3. Один, два, три, четыре, пять –
- 4. Ряд чисел 1, 2, 3, 4, 5,
- 5. Архимед «Псаммит, или Исчисление песчинок» Архимеду удалось
- 6. Наибольшее число системы Архимеда содержит 84016 нулей.
- 7. Пифагор (ок. 580 –500 г. до н.э.)
- 8. 2 +
- 9. «Божественное» число 7
- 10. Пифагорейцы показали, как заполнить плоскость системами правильных
- 11. Интересными свойствами обладают числа: 135 =
- 12. 37 * 3 = 111 37
- 13. Сумма любого количества последовательных нечетных чисел, начиная
- 14. Сумма кубов натурального ряда чисел, начиная с
- 15. Тройки Пифагора 3 4 5 S
- 16. Гаусс
- 17. Видит тот, кто хочет
- 18. Вывод: Многие ученики недооценивают математику, не видят
Слайд 2Цель работы:
показать красоту и раскрыть тайну чисел натурального
ряда.
Задачи:
изучить свойства натуральных чисел, раскрыть закономерности,
повысить уровень вычислительных навыков.
Задачи:
изучить свойства натуральных чисел, раскрыть закономерности,
повысить уровень вычислительных навыков.
Слайд 4Ряд чисел 1, 2, 3, 4, 5, 6, 7, 8… называется
натуральным, а сами эти числа – натуральными.
Возник этот ряд на заре цивилизации из практических нужд людей как результат счета предметов.
Это был первый шаг к созданию математики.
Возник этот ряд на заре цивилизации из практических нужд людей как результат счета предметов.
Это был первый шаг к созданию математики.
Слайд 5Архимед «Псаммит, или Исчисление песчинок»
Архимеду удалось расширить ряд натуральных чисел до
небывалых размеров, он, пользуясь созданной им самим системой счисления, подсчитал число песчинок, наполняющих шар радиусом151012 км. Это число содержит 84016 нулей.
Слайд 7Пифагор (ок. 580 –500 г. до н.э.)
В школе Пифагора процветала числовая
мистика, пифагорейцы обожествляли число.
Слайд 10Пифагорейцы показали, как заполнить плоскость системами правильных треугольников, квадратов или правильных
шестиугольников, а пространство – системой кубов.
Слайд 11Интересными свойствами обладают числа:
135 = (1 + 3 + 5) *
1 * 3 * 5
144 = (1 + 4 + 4) * 1 * 4 * 4
Эти числа равны произведению своих цифр на сумму этих цифр.
144 = (1 + 4 + 4) * 1 * 4 * 4
Эти числа равны произведению своих цифр на сумму этих цифр.
Слайд 1237 * 3 = 111
37 * 6 = 222
37 * 9 = 333
37 * 12 = 444
37 * 15 = 555
37 * 18 = 666
37 * 21 = 777
37 * 24 = 888
37 * 27 = 999
Слайд 13Сумма любого количества последовательных нечетных чисел, начиная с 1, всегда дает
точный квадрат.
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25
Слайд 14Сумма кубов натурального ряда чисел, начиная с 1, равна квадрату суммы
этих чисел
13 + 23 = (1+2)2
13 + 23 + 33 = (1+2+3)2
13 + 23 + 33 + 43 = (1+2+3+4)2
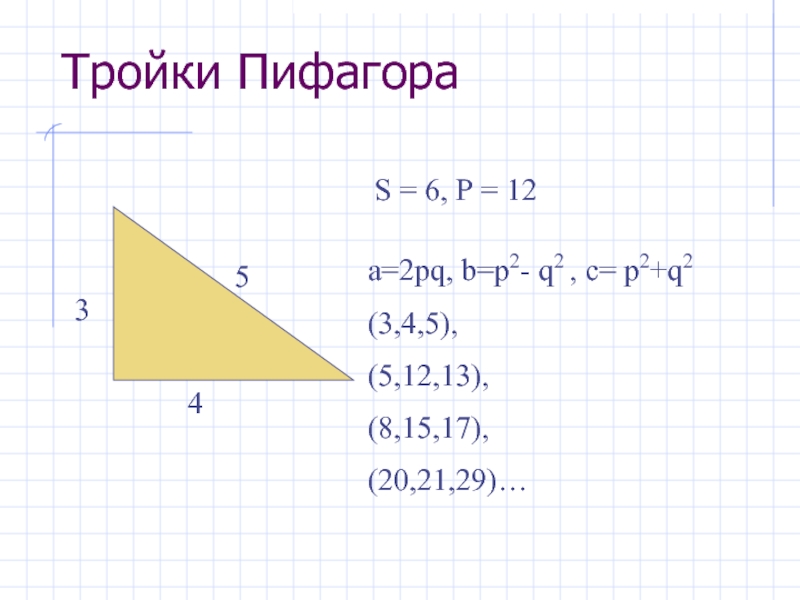
Слайд 15Тройки Пифагора
3
4
5
S = 6, P = 12
a=2pq, b=p2- q2 , c=
p2+q2
(3,4,5),
(5,12,13),
(8,15,17),
(20,21,29)…
(3,4,5),
(5,12,13),
(8,15,17),
(20,21,29)…
Слайд 18Вывод:
Многие ученики недооценивают математику, не видят её красоты. Данный проект составлен
на необычную тему, для привлечения внимания к математике остальных. Тех, кто ещё не увидел её с другой, красивой и таинственной стороны.