- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи В4 презентация
Содержание
- 1. Задачи В4
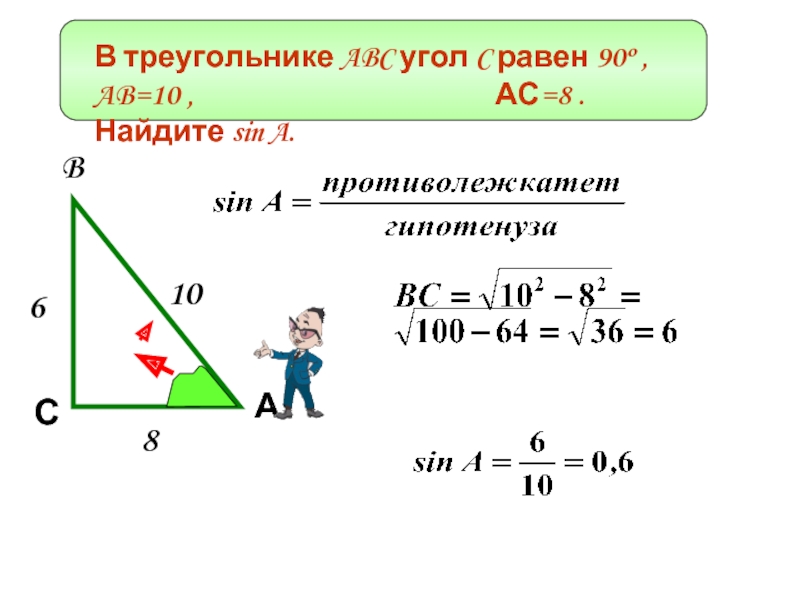
- 2. В треугольнике ABC угол C равен
- 3. В треугольнике ABC угол C
- 4. В треугольнике ABC угол C
- 5. С 5
- 6. А В параллелограмме АВСD высота, опущенная на
- 7. Найдите tg A Найдите соs A
- 8. В треугольнике ABC угол C равен
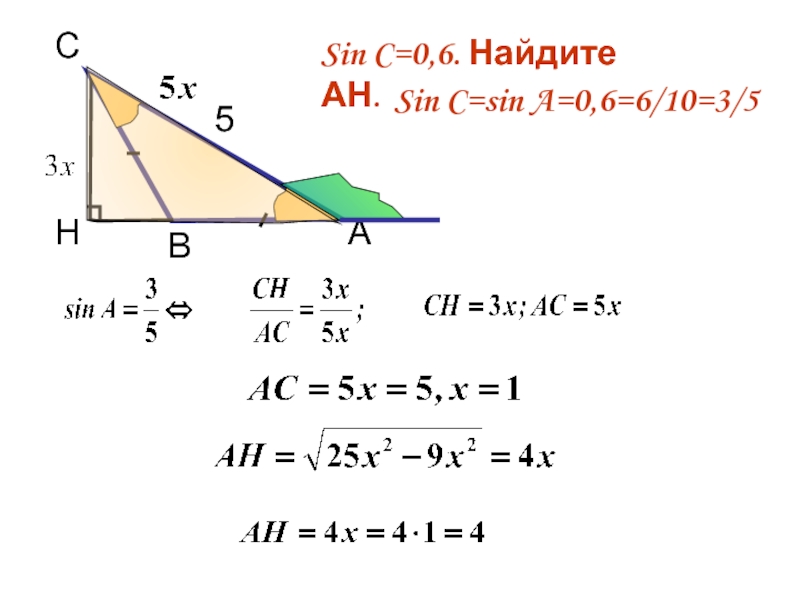
- 9. А С Н 4 5
- 10. С 5
- 11. Отрезки касательных к окружности, проведённые из
- 12. B4 (№ 54689) К окружности, вписанной
- 13. B4 (№ 54309) Окружность, вписанная в равнобедренный
- 14. В четырёхугольник можно вписать окружность тогда
- 15. B4 (№ 54599) В четырехугольник ABCD
- 16. № 54639 1х+14х=9х+… Р=30х=150, х=5 14х=14·5=70
- 17. Центральный угол равен дуге,на которую опирается,
- 18. Медиана прямоугольного треугольника, проведённая с
- 19. Около четырёхугольника можно описать окружность тогда и
- 20. Два угла вписанного в окружность четырёхугольника равны
- 21. Сторона AB треугольника ABC равна
Слайд 4
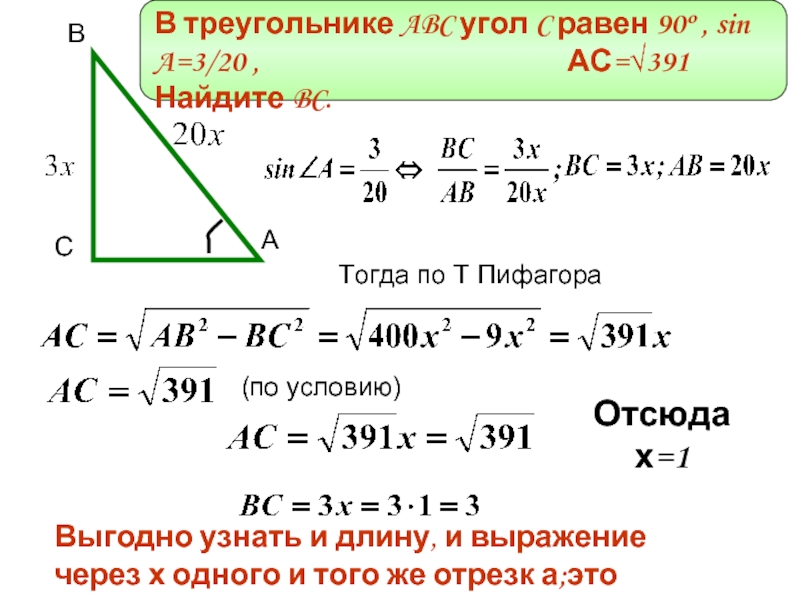
В треугольнике ABC угол C равен 90º , sin A=3/20 ,
С
В
А
Тогда по Т Пифагора
Отсюда х=1
(по условию)
Выгодно узнать и длину, и выражение через х одного и того же отрезк а;это поможет узнать величину х.
Слайд 5
С
5
4
А
Н
В
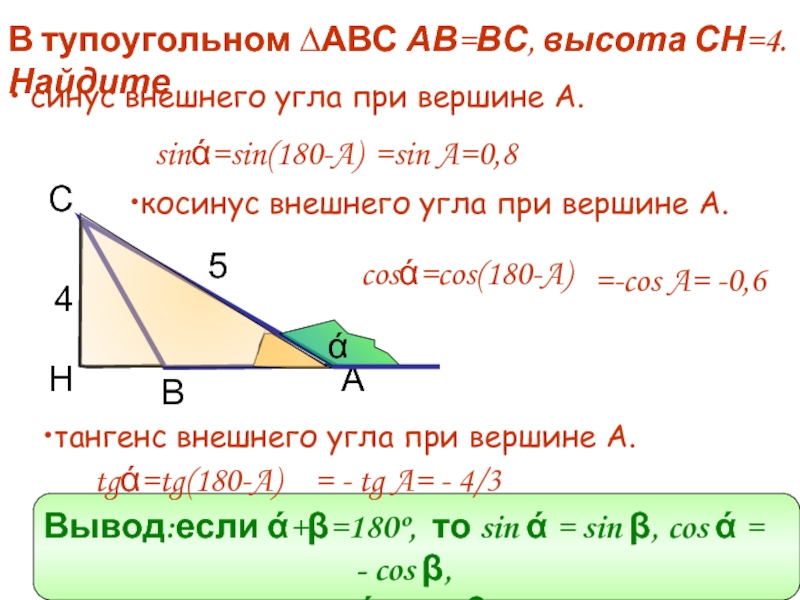
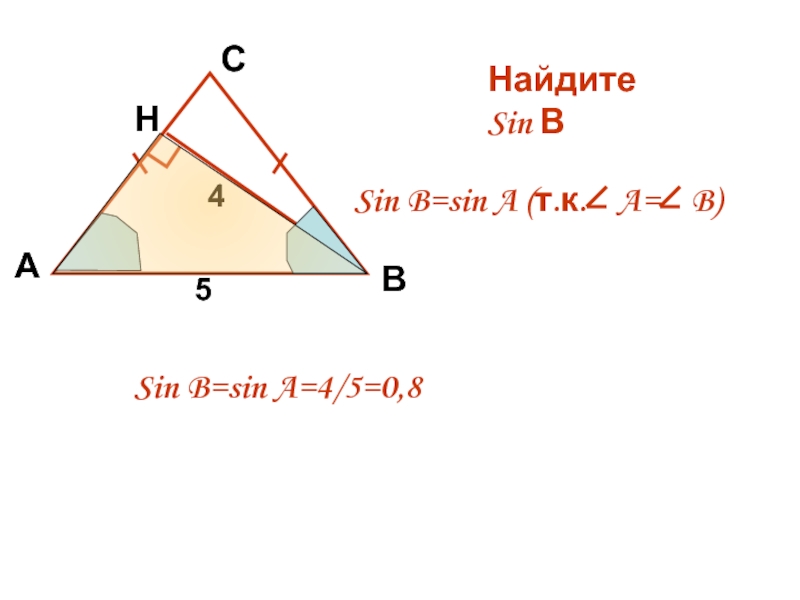
В тупоугольном ∆АВС АВ=ВС, высота СН=4. Найдите
косинус внешнего угла при вершине
синус внешнего угла при вершине А.
тангенс внешнего угла при вершине А.
ά
sinά=sin(180-A)
=sin A=0,8
cosά=cos(180-A)
=-cos A= -0,6
tgά=tg(180-A)
= - tg A= - 4/3
Вывод:если ά+β=180º, то sin ά = sin β, cos ά = - cos β, tg ά = - tg β
Слайд 6А
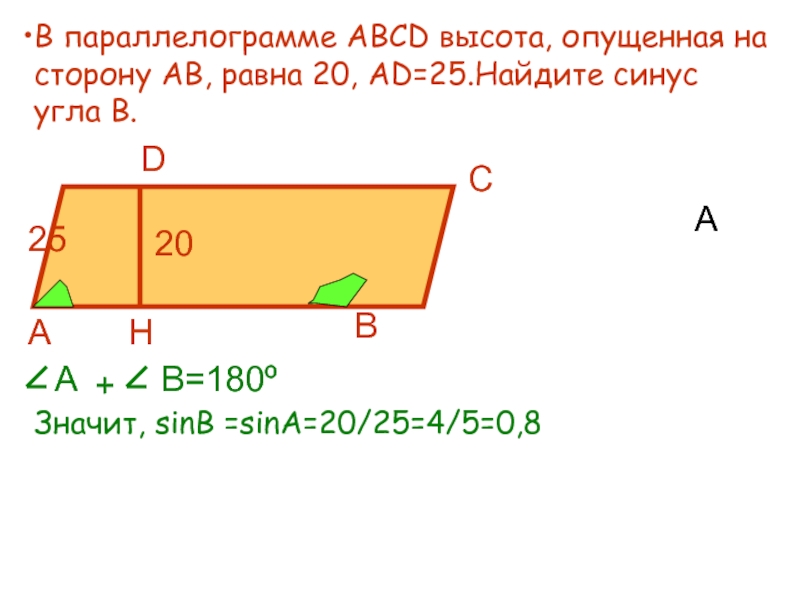
В параллелограмме АВСD высота, опущенная на сторону АВ, равна 20, АD=25.Найдите
Значит, sinB =sinA=20/25=4/5=0,8
20
25
Слайд 7
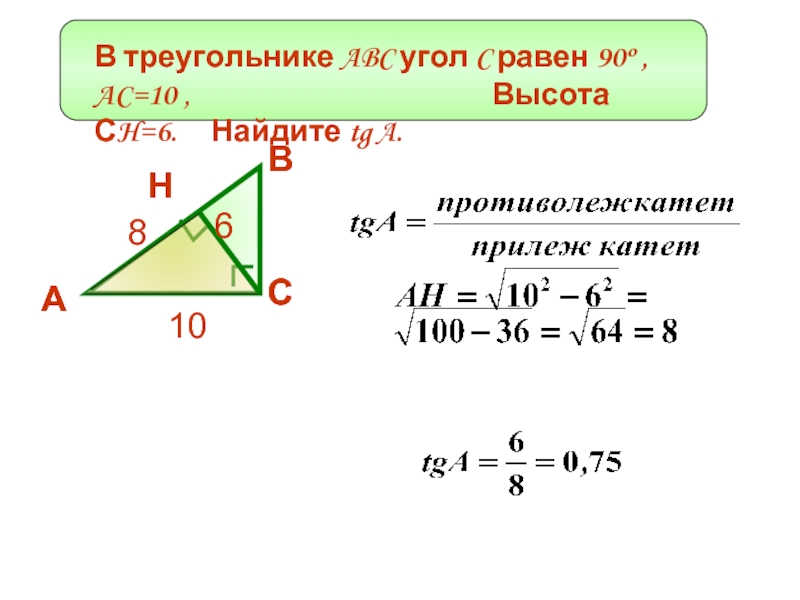
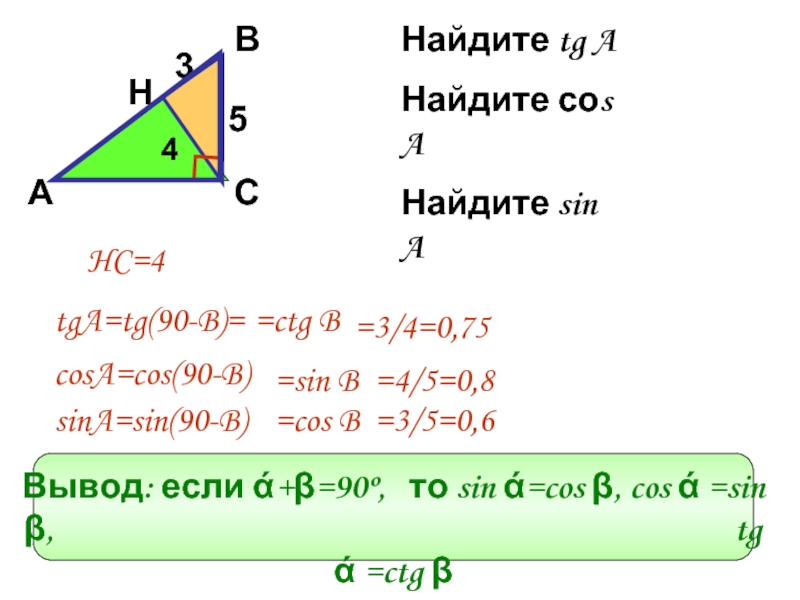
Найдите tg A
Найдите соs A
Найдите sin A
tgA=tg(90-B)=
=ctg B
cosA=cos(90-B)
=sin B
sinA=sin(90-B)
=cos B
=3/4=0,75
=4/5=0,8
=3/5=0,6
HC=4
Вывод:
4
Слайд 8
В треугольнике ABC угол C равен 90º, СH-высота ,
cos A=0,8
Н
С
А
В
С
А
В
Н
10x
6
8x
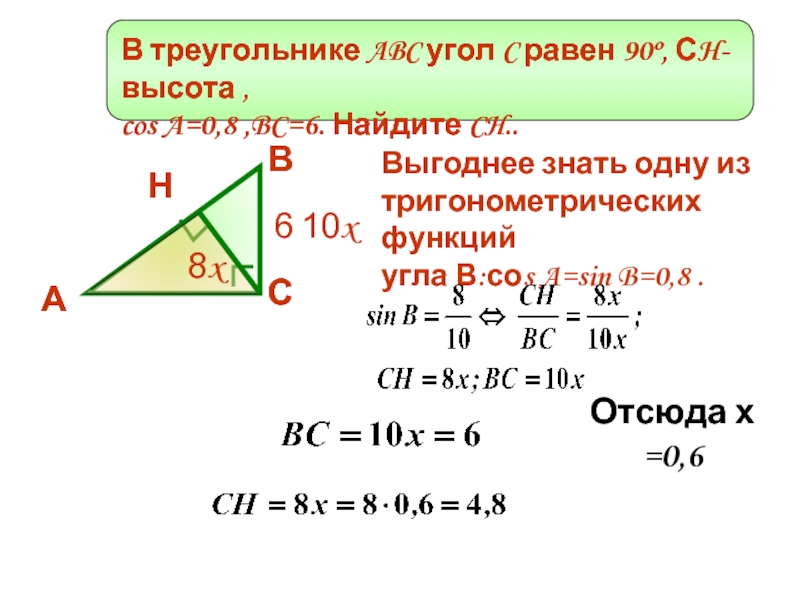
Выгоднее знать одну из
тригонометрических функций
угла В:соs A=sin B=0,8 .
Отсюда х =0,6
В треугольнике ABC угол C равен 90º, СH-высота ,
cos A=0,8 ,BC=6. Найдите CH..
Слайд 11
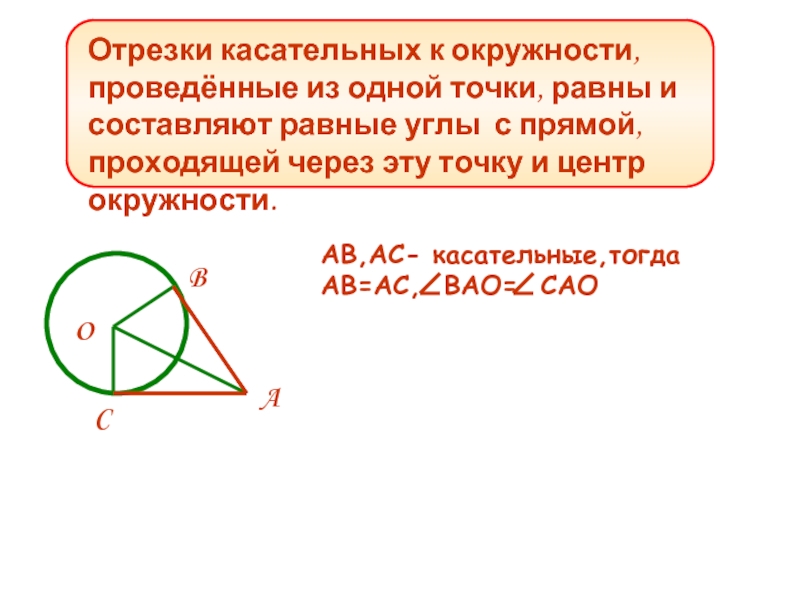
Отрезки касательных к окружности, проведённые из одной точки, равны и составляют
A
O
C
B
AB,AC- касательныe,тогда
AB=AC, BAO= CAO
Слайд 12
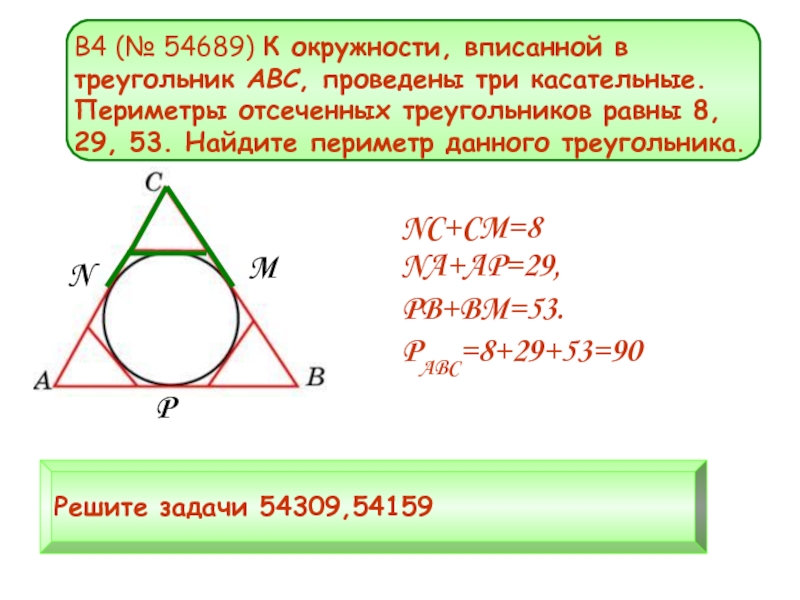
B4 (№ 54689) К окружности, вписанной в треугольник ABC, проведены три
N
M
NC+CM=8
P
NA+AP=29, PB+BM=53.
PABC=8+29+53=90
Решите задачи 54309,54159
Слайд 13B4 (№ 54309) Окружность, вписанная в равнобедренный треугольник, делит в точке
Р=(2+21)·2+(2+2)=50
(№ 54159) Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 22. Найдите гипотенузу c этого треугольника. В ответе укажите
.
22
х
22
х
21
2
Слайд 14
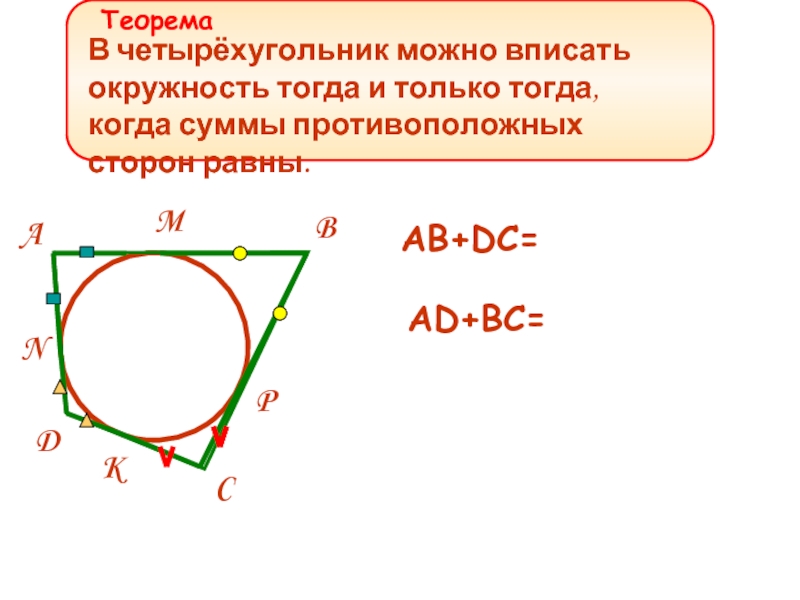
В четырёхугольник можно вписать окружность тогда и только тогда, когда суммы
P
K
N
M
D
C
B
A
AB+DC=
AD+BC=
Теорема
Слайд 15
B4 (№ 54599) В четырехугольник ABCD вписана окружность,
АВ=6, ВС=2, СД=14.
A
B
C
D
AB+CD=AD+DC=
6+14=AD+2
AD=20-2=18
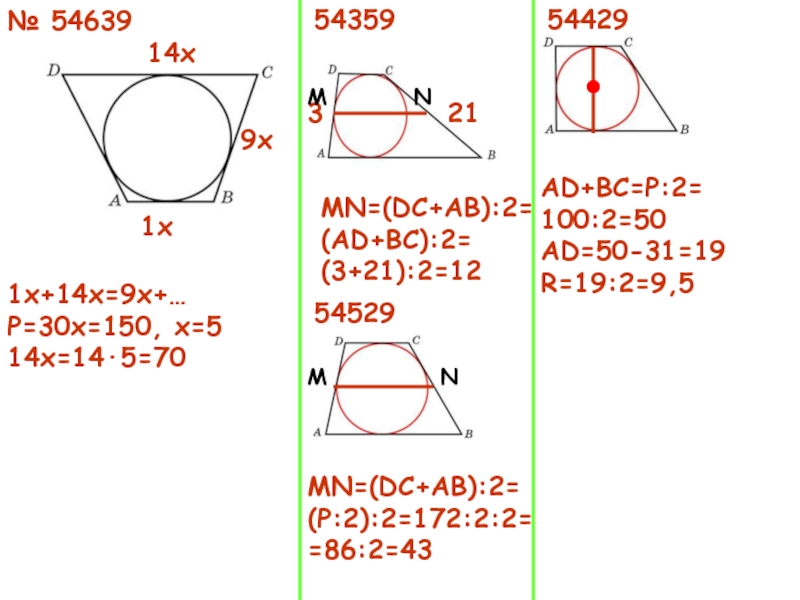
Слайд 16№ 54639
1х+14х=9х+…
Р=30х=150, х=5
14х=14·5=70
54359
1х
9х
14х
21
3
МN=(DC+AB):2=
(AD+BC):2=
(3+21):2=12
54529
N
M
МN=(DC+AB):2=
(P:2):2=172:2:2=
=86:2=43
54429
AD+BC=P:2=
100:2=50
AD=50-31=19
R=19:2=9,5
Слайд 17
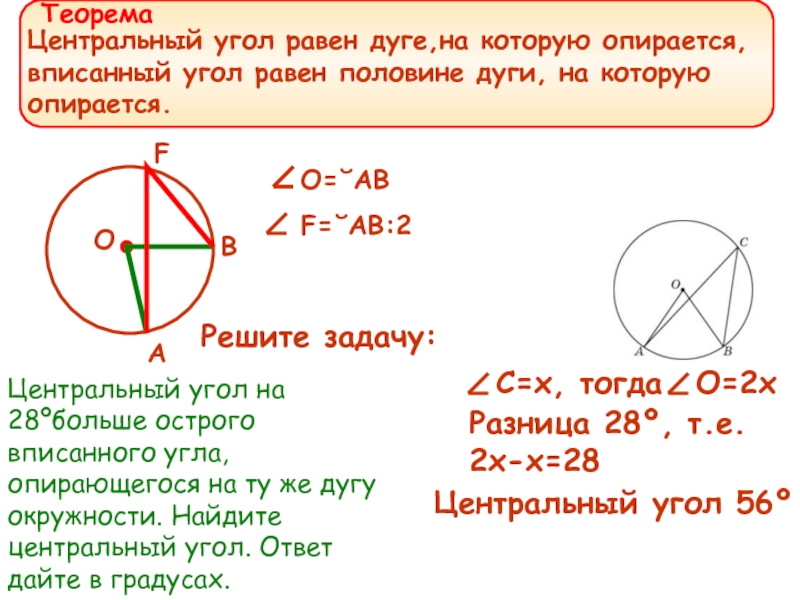
Центральный угол равен дуге,на которую опирается,
вписанный угол равен половине дуги,
O=˘AB
F=˘AB:2
Центральный угол на 28ºбольше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите центральный угол. Ответ дайте в градусах.
Решите задачу:
Теорема
Слайд 18
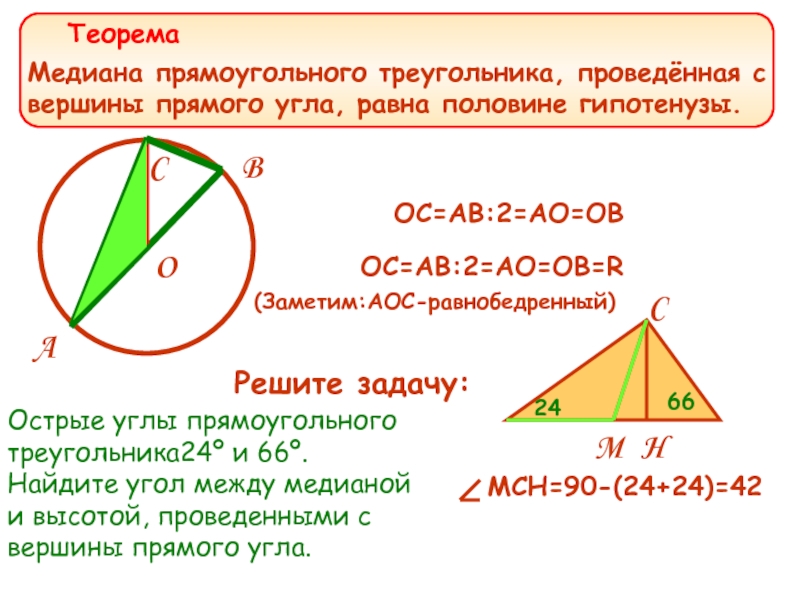
Медиана прямоугольного треугольника, проведённая с вершины прямого угла, равна половине гипотенузы.
OC=AB:2=AO=OB
O
C
B
A
OC=AB:2=AO=OB=R
Решите задачу:
Острые углы прямоугольного треугольника24º и 66º. Найдите угол между медианой и высотой, проведенными с вершины прямого угла.
24
66
(Заметим:AOC-равнобедренный)
M
C
H
MCH=90-(24+24)=42
Теорема
Слайд 19Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы
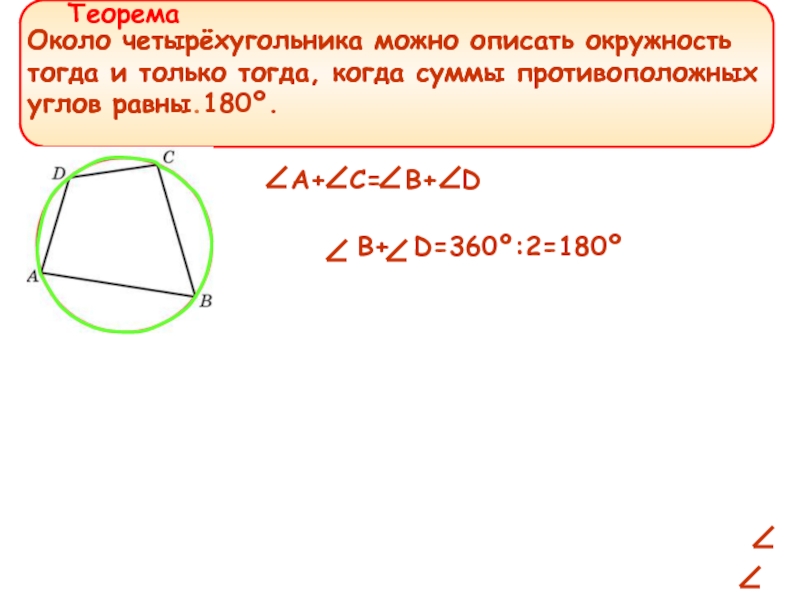
Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны.
Около четырёхугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны 180º.
А+ С= В+ D
В+ D=360º:2=180º
Теорема
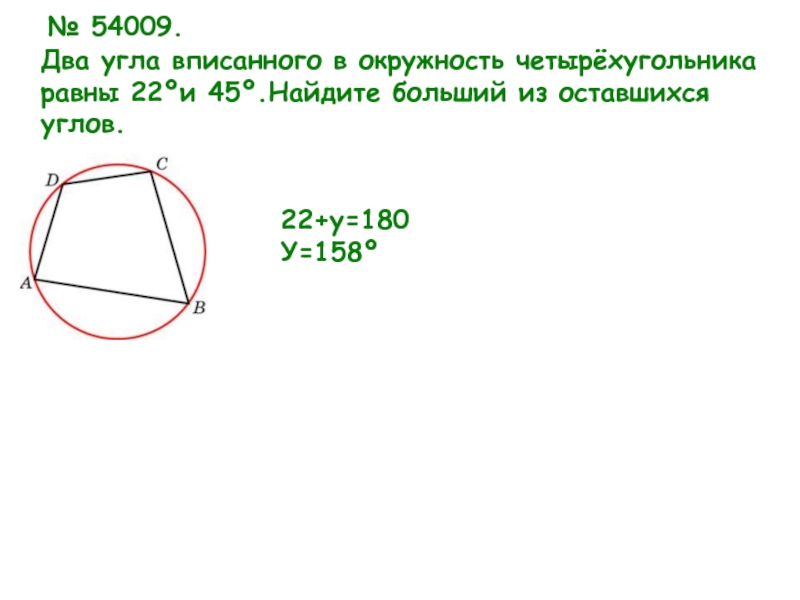
Слайд 20Два угла вписанного в окружность четырёхугольника равны 22ºи 45º.Найдите больший из
№ 54009.
22+у=180
У=158º
Слайд 21
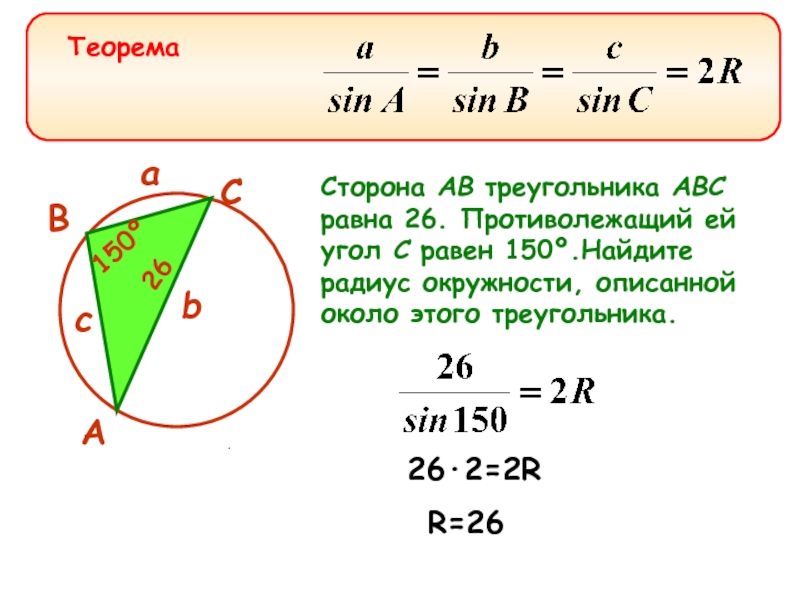
Сторона AB треугольника ABC равна 26. Противолежащий ей угол C равен
26·2=2R
R=26
Теорема