Задачи поиска в структурах данных презентация

Содержание

Задачи поиска в структурах данных Кроме поиска совпадению аргумента поиска с ключом записи, существует поиск по близости аргумента и ключа и поиск по интервалу, означающий попадание

Слайд 1Задачи поиска в структурах данных
Поиск - нахождение какой-либо конкретной информации

в большом объеме ранее собранных данных.
Данные делятся на записи, и каждая запись имеет хотя бы один ключ. Ключ используется для того, чтобы отличить одну запись от другой.
Целью поиска является нахождение всех записей подходящих к заданному ключу поиска.

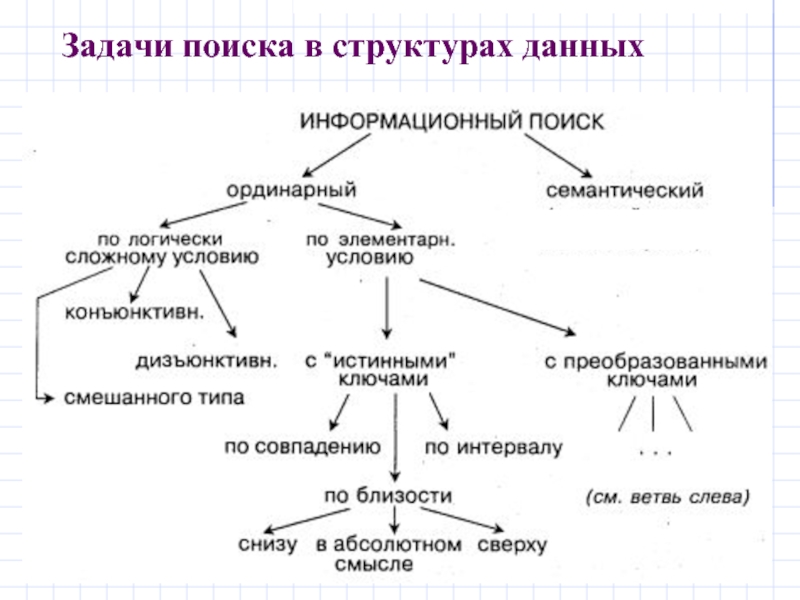
Слайд 2Задачи поиска в структурах данных

Кроме поиска совпадению аргумента

поиска с ключом записи, существует поиск по близости аргумента и ключа и поиск по интервалу, означающий попадание ключа в заданный двумя аргументами (границами) интервал.
Логически сложные условия поиска могут быть конъюнктивными (обязательно выполнение в искомых записях всех заданных элементарны условий), дизъюнктивными (достаточно выполнения одного из них) смешанной природы.

Слайд 3Задачи поиска в структурах данных

d

Слайд 4Задачи поиска в структурах данных
Var a:

array[0..N -1] of Item;
Item описывает запись с некоторым полем, играющим роль ключа.
Задача заключается в поиске элемента, ключ которого равен заданному аргументу поиска x



Слайд 5Задачи поиска в структурах данных
Полученный в результате индекс i,

удовлетворяющий условию а[i].key = x, обеспечивает доступ к другим полям обнаруженного элемента.

Так как мы рассматриваем, прежде всего, сам процесс поиска, то мы будем считать, что тип Item включает только ключ key


Слайд 6Линейный поиск
Если нет никакой дополнительной информации о разыскиваемых данных, то

очевидный подход - простой последовательный просмотр массива с увеличением шаг за шагом той его части, где желаемого элемента не обнаружено.

Такой метод называется линейным поиском



Слайд 7Линейный поиск
Алгоритм 1.
i:=0;

while (iх) do
i:=i+1;



Слайд 8Линейный поиск
Алгоритм 2.( алгоритм линейного

поиска с барьером )
а: array[0..N] of integer

a[N]:=x; i:=0;
while a[i]<>x do
i:=i+1;




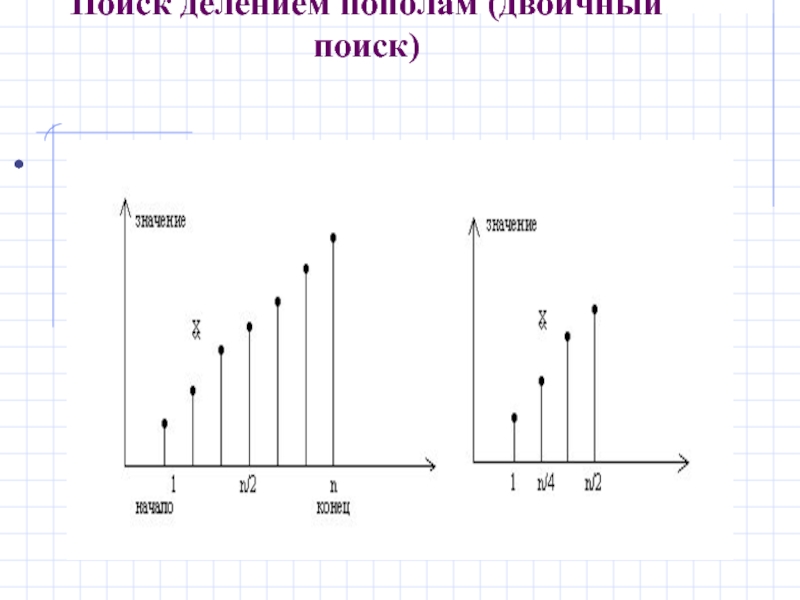
Слайд 9 Поиск делением пополам (двоичный поиск)
массив A упорядочен, т. е.

удовлетворяет условию
ak-1≤ ak, 1≤ k< N





Слайд 10 Поиск делением пополам (двоичный поиск)






Слайд 11 Поиск делением пополам (двоичный поиск)
L:=0; R:=N-1; Found:=false;
while(L

do
begin
         m:=(L+R) div 2;
         if a[m]=x then Found:= true
                         else
                            if a[m] else R:=m-1
                    
end;






Слайд 12 Поиск делением пополам (двоичный поиск)
Максимальное число сравнений для этого

алгоритма равно log2n

Линейный поиск - N/2







Слайд 13 Поиск делением пополам (двоичный поиск)
Быстрый алгоритм
L:=0; R:=N;
while L


begin
           m:=(L+R) div 2;
           if а[m] then L:=m+1
else R:=m
end;
If a[R] = x then …. {элемент найден}





Слайд 14 Поиск в таблице
Поиск в массиве иногда называют поиском в

таблице, особенно если ключ сам является составным объектом, таким, как массив чисел или символов
Type String = array[0..М-1] of char;
отношение порядка для строк x и y:
x = y, если xj = yj для 0=< j < M
x < y, если xi < yi для 0=< i < M
и xj = yj для 0 =< j < i





Слайд 15 Поиск в таблице
Схема поиска с концевым символом


i:=0;
while (x[i]=y[i])

and (x[i]<>*) do i:=i+1

Концевой символ работает здесь как барьер





Слайд 16 Поиск в таблице
Пусть таблица T и аргумент поиска

x определяются следующим образом:

T: array[0..N-1] of String;
x: String;
Пусть N достаточно велико и таблица упорядочена в алфавитном порядке





Слайд 17 Поиск в таблице
L:=0; R:=N;
while L

begin
             m:=(L+R) div 2; i:=0;
           while (T[m,i]=x[i]) and (x[i]<>*) do i:=i+1;
              if T[m,i] end;






Слайд 18 Поиск в таблице
if R

begin
           i:=0;
           while (T[R,i]=х[i]) and (х[i]<>*) do
i:=i+1
end
{(R





Слайд 19 Прямой поиск строки
Пусть задан массив s из

N элементов и массив p из M элементов, причем 0 < M =< N. Описаны они так:
s: array[0..N-1] of Item
р: array[0..M-1] of Item

Поиск строки обнаруживает первое вхождение p в s.





Слайд 20 Прямой поиск строки
Алгоритм прямого поиска

i:=-1;
repeat
           i:=i+1; j:=0;
           while (j j:=j+1;
until (j=M) or (i=N-M)



Слайд 21 Алгоритм Кнута, Мориса и Пратта



R


F



Слайд 22 Алгоритм Кнута, Мориса и Пратта



Слайд 23 Алгоритм Кнута, Мориса и Пратта
Общая схема КМП-алгоритма


i:= 0; j:=0;
While (j begin
While (j>=0) and (s[i] <>p[j]) do
j:=d;
i:= i+1; j := j+1
end
shift

Слайд 24 Алгоритм Кнута, Мориса и Пратта
Program KMP;

const
        Mmax = 100; Nmax = 10000;
var
        i, j, k, M, N: integer;
        p: array[0..Mmax-1] of char; {слово}
        s: array[0..Nmax-1] of char; {текст}
        d: array[0..Mmax-1] of integer;


Слайд 25 Алгоритм Кнута, Мориса и Пратта
begin

{Ввод текста s и слова p}
Write('N:'); Readln(N);
Write('s:'); Readln(s);
Write('M:'); Readln(M);
Write('p:'); Readln(p);
{Заполнение массива d}
j:=0; k:=-1; d[0]:=-1;


Слайд 26 Алгоритм Кнута, Мориса и Пратта
while j


begin
            while(k>=0) and (p[j]<>p[k]) do
k:=d[k];
            j:=j+1; k:=k+1;
            if p[j]=p[k] then d[j]:=d[k]
            else d[j]:=k;
end;



Слайд 27 Алгоритм Кнута, Мориса и Пратта
{Поиск слова p

в тексте s}

i:=0; j:=0;
while (j begin
         while (j>=0) and (s[i]<>p[j]) do
j:=d[j]; {Сдвиг слова}
          i:=i+1; j:=j+1;
end;




Слайд 28 Алгоритм Кнута, Мориса и Пратта
{Вывод результата

поиска}
if j=M then Writeln('Yes') {найден }
else Writeln('No'); {не найден}
Readln;
end.
Число сравнений – m+n





Слайд 29 Алгоритм Боуера и Мура






Слайд 30 Алгоритм Боуера и Мура






Program BM;
const
        Mmax = 100; Nmax = 10000;
var
        i, j, k, M, N: integer;
         ch: char;
        p: array[0..Mmax-1] of char; {слово}
       s: array[0..Nmax-1] of char; {текст}
        d: array[' '..'z'] of integer;

Слайд 31 Алгоритм Боуера и Мура







begin
{Ввод текста s и слова p}
Write('N:'); Readln(N);
Write('s:'); Readln(s);
Write('M:'); Readln(M);
Write('p:'); Readln(p);
{Заполнение массива d}
for ch:=' ' to 'z' do d[ch]:=M;

Слайд 32 Алгоритм Боуера и Мура
for j:=0 to M-2 do

d[p[j]]:=M-j-1;
i:=M;
repeat
          j:=M; k:=i;
          repeat {Цикл сравнения символов }
                     k:=k-1; j:=j-1; {слова, начиная с правого.}
          until (j<0) or (p[j]<>s[k]); {Выход, если сравнили все}
          {слово или несовпадение. }
          i:=i+d[s[i-1]]; {Сдвиг слова вправо }
until (j<0) or (i>N);









Слайд 33 Алгоритм Боуера и Мура

{Вывод результата поиска}
if j<0 then Writeln('Yes') {найден }
else Writeln('No'); {не найден}
Readln;
end.









Похожие презентации

Керамические материалы. Стекло и материалы на основе стекла 1260
Киноклуб Подросток 293
Литий-ионные аккумуляторы – зеленая экономика 271
РОССИЙСКАЯ АКАДЕМИЯ НАУК ИНСТИТУТ МИРОВОЙ ЭКОНОМИКИ И МЕЖДУНАРОДНЫХ ОТНОШЕНИЙ Прогноз развития мировой экономики2006 – 2020 гг . 208
5 Cars To Keep Your New Year's Resolution 193
"О, весна без конца и без краю..." 409

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика