- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Взаимное расположение прямых и плоскостей в пространстве презентация
Содержание
- 1. Взаимное расположение прямых и плоскостей в пространстве
- 2. Взаимное расположение прямых в пространстве Возможны три
- 3. Аксиомы стереометрии А1 Через любые три точки,
- 4. А2 Если две точки прямой лежат в
- 5. А3 Если две плоскости имеют
- 6. Параллельность прямой и плоскости Если две точки
- 7. Признак или теорема о параллельности прямой и
- 8. Параллельность плоскостей Итак, мы
- 9. Теорема Если две пересекающиеся прямые одной
Взаимное расположение прямых в пространстве Возможны три случая взаимного расположения двух прямых в пространстве: - прямые пересекаются, т.е. имеют только одну общую точку - прямые параллельны, т.е. лежат в
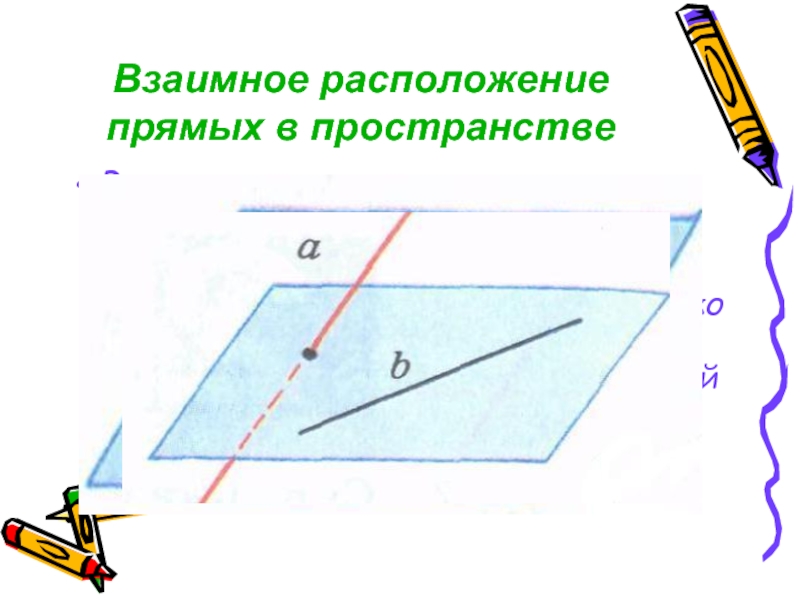
Слайд 2Взаимное расположение прямых в пространстве
Возможны три случая взаимного расположения двух прямых
в пространстве:
- прямые пересекаются, т.е. имеют только одну общую точку
- прямые параллельны, т.е. лежат в одной плоскости и не пересекаются
- прямые скрещиваются, т.е. не лежат в одной плоскости
- прямые пересекаются, т.е. имеют только одну общую точку
- прямые параллельны, т.е. лежат в одной плоскости и не пересекаются
- прямые скрещиваются, т.е. не лежат в одной плоскости
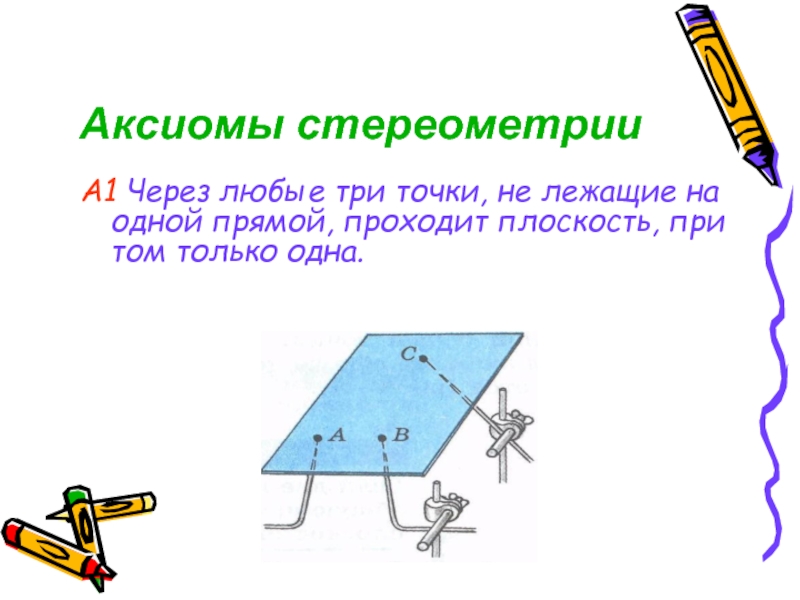
Слайд 3Аксиомы стереометрии
А1 Через любые три точки, не лежащие на одной прямой,
проходит плоскость, при том только одна.
Слайд 4А2 Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ними и поверхностью стола образуется просвет.
Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки. С этой целью линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный (прямолинейный), то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ними и поверхностью стола образуется просвет.
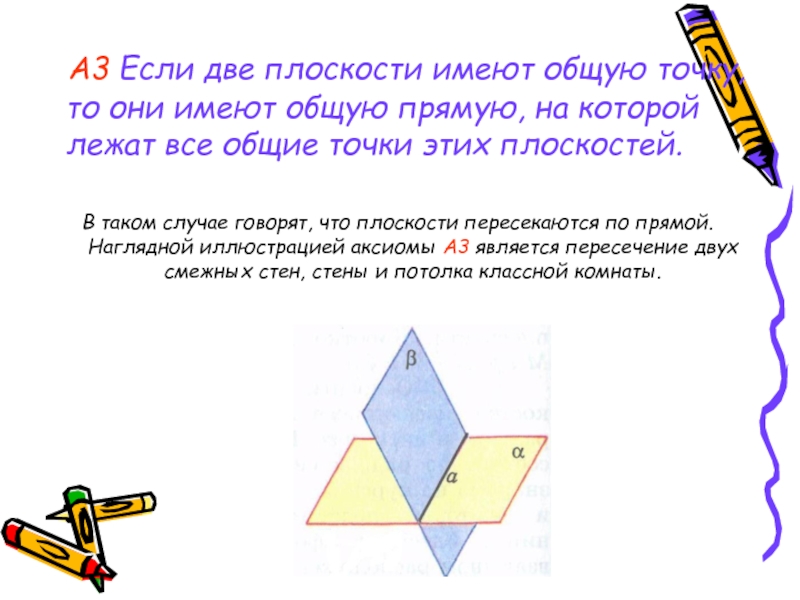
Слайд 5 А3 Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, что плоскости пересекаются по прямой. Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
В таком случае говорят, что плоскости пересекаются по прямой. Наглядной иллюстрацией аксиомы А3 является пересечение двух смежных стен, стены и потолка классной комнаты.
Слайд 6Параллельность прямой и плоскости
Если две точки прямой лежат в данной плоскости,
то согласно А2 вся прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:
а) прямая лежит плоскости
б) прямая и плоскость имеют одну общую точку, т. е. пересекаются
в) прямая и плоскость не имеют ни одной общей точки
а) прямая лежит плоскости
б) прямая и плоскость имеют одну общую точку, т. е. пересекаются
в) прямая и плоскость не имеют ни одной общей точки
Слайд 7Признак или теорема о параллельности прямой и плоскости
Если прямая, не лежащая
в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Слайд 8Параллельность плоскостей
Итак, мы знаем что если две плоскости имеют общую
точку, то они пересекаются по прямой (аксиома А3). Отсюда следует, что две плоскости либо пересекаются по прямой, либо не пересекаются, т. е. не имеют ни одной общей точки.
Определение
Две плоскости называются параллельными, если они не пересекаются.
Представление о параллельных плоскостях дают пол и потолок комнаты, две противоположные стены, поверхность стола и плоскость пола.
Определение
Две плоскости называются параллельными, если они не пересекаются.
Представление о параллельных плоскостях дают пол и потолок комнаты, две противоположные стены, поверхность стола и плоскость пола.
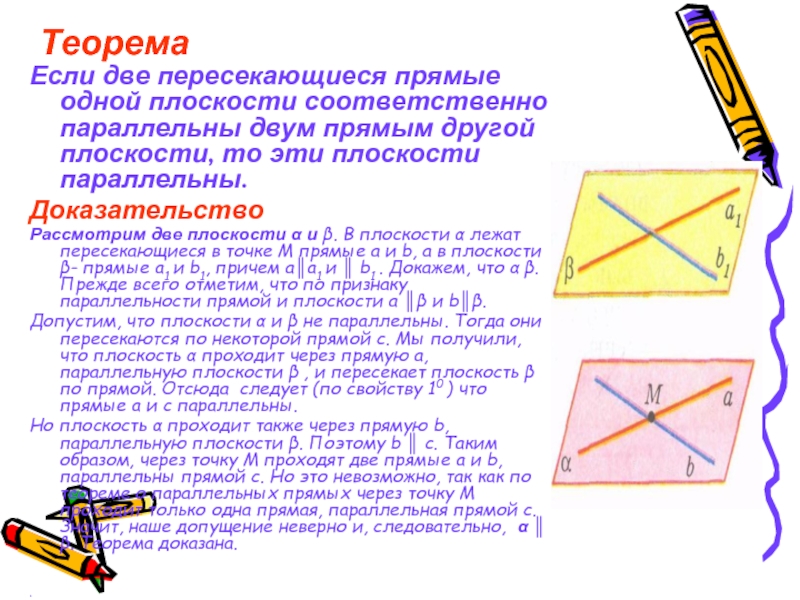
Слайд 9 Теорема
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым
другой плоскости, то эти плоскости параллельны.
Доказательство
Рассмотрим две плоскости α и β. В плоскости α лежат пересекающиеся в точке М прямые a и b, а в плоскости β- прямые a1 и b1, причем а║а1 и ║ b1 . Докажем, что α β. Прежде всего отметим, что по признаку параллельности прямой и плоскости а ║β и b║β.
Допустим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой с. Мы получили, что плоскость α проходит через прямую а, параллельную плоскости β , и пересекает плоскость β по прямой. Отсюда следует (по свойству 10 ) что прямые а и с параллельны.
Но плоскость α проходит также через прямую b, параллельную плоскости β. Поэтому b ║ с. Таким образом, через точку М проходят две прямые а и b, параллельны прямой с. Но это невозможно, так как по теореме о параллельных прямых через точку М проходит только одна прямая, параллельная прямой с. Значит, наше допущение неверно и, следовательно, α ║ β. Теорема доказана.
.
Доказательство
Рассмотрим две плоскости α и β. В плоскости α лежат пересекающиеся в точке М прямые a и b, а в плоскости β- прямые a1 и b1, причем а║а1 и ║ b1 . Докажем, что α β. Прежде всего отметим, что по признаку параллельности прямой и плоскости а ║β и b║β.
Допустим, что плоскости α и β не параллельны. Тогда они пересекаются по некоторой прямой с. Мы получили, что плоскость α проходит через прямую а, параллельную плоскости β , и пересекает плоскость β по прямой. Отсюда следует (по свойству 10 ) что прямые а и с параллельны.
Но плоскость α проходит также через прямую b, параллельную плоскости β. Поэтому b ║ с. Таким образом, через точку М проходят две прямые а и b, параллельны прямой с. Но это невозможно, так как по теореме о параллельных прямых через точку М проходит только одна прямая, параллельная прямой с. Значит, наше допущение неверно и, следовательно, α ║ β. Теорема доказана.
.
