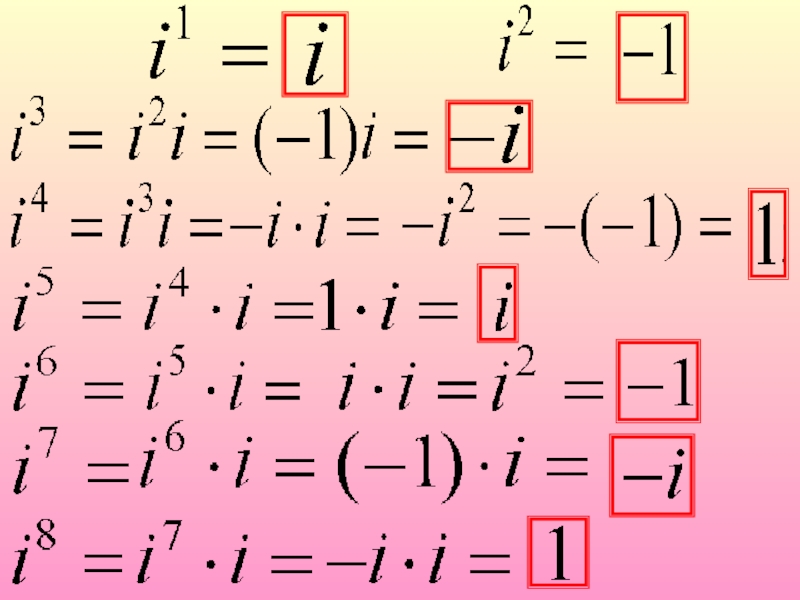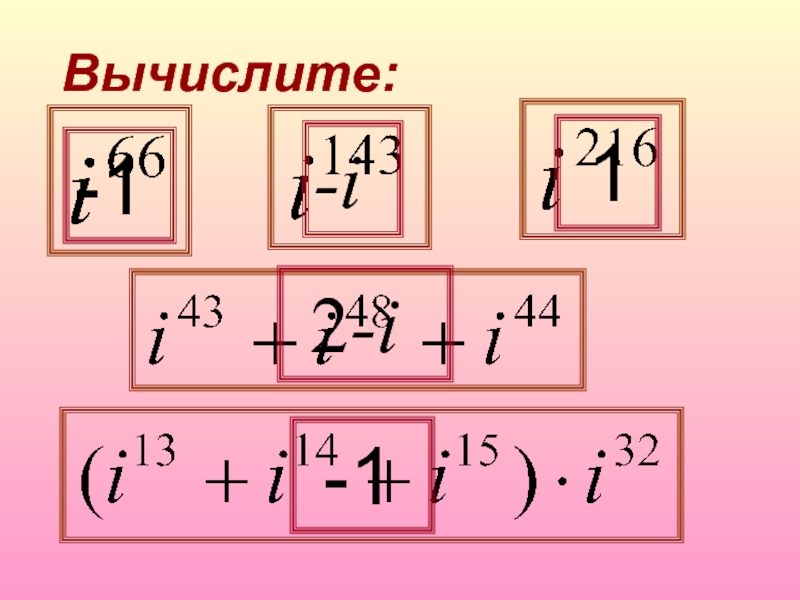
Вычислите: презентация

Содержание

1. Вычислите:
2. Мнимая единица
3. Например, Вычислите:
5. Значения степеней числа i повторяются
6. Решение.
7. Вычислите: -1
8. Комплексные числа Определение 1. Числа
9. VII в.н.э.- квадратный корень из положительного числа
10. В XVI веке в связи с
11. Он предложил
12. в 1572 году итальянский
13. Название “мнимые числа” ввёл
14. один из крупнейших математиков
15. гораздо В настоящее время
16. Комплексные числа имеют прикладное значение
17. Применяются при
18. При вычерчивании географических карт
19. В исследовании
20. a + bi = c + di,
21. Решение. Согласно условию равенства комплексных чисел
22. (а+bi)
23. Выполните действия: z1 = 2 + 3i,
24. Умножение (c+di) = ac bс i =
25. Выполните действия: (5 + 3i)(5 –
26. Определение 3. Два комплексных числа называются
27. Деление = = =
28. Выполните действия: = = = 2
29. Домашняя работа 2) Найти x

Мнимая единица i – начальная буква французского слова imaginaire – «мнимый»

Слайд 1Вычислите:

Слайд 2Мнимая единица
i – начальная буква французского слова

imaginaire – «мнимый»

Слайд 3Например,

Вычислите:

Слайд 4

Слайд 5
Значения степеней числа i
повторяются с периодом,

равным 4.

Найдем:

Слайд 6
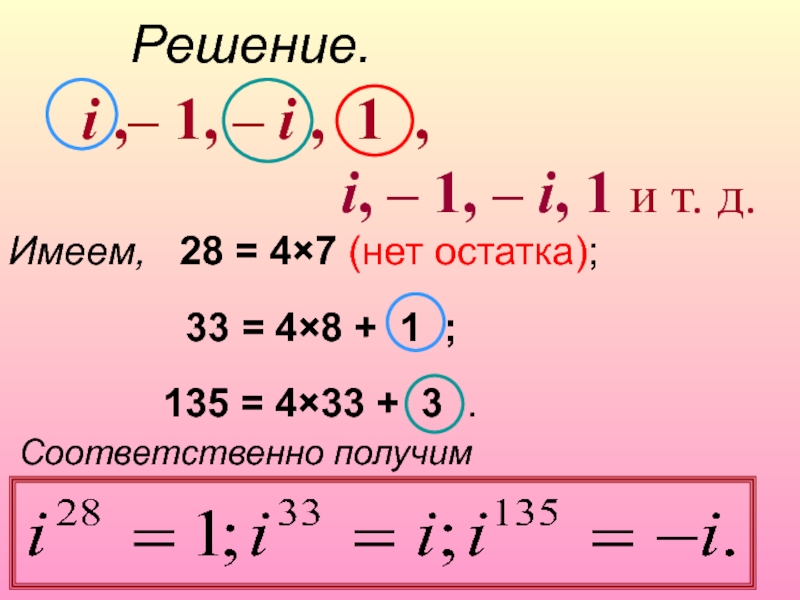
Решение.
i ,– 1, – i ,

1 ,
i, – 1, – i, 1 и т. д.
Имеем, 28 = 4×7 (нет остатка);

33 = 4×8 + 1 ;

135 = 4×33 + 3 .
Соответственно получим

Слайд 7Вычислите:

-1
-i
1
2-i
-1

Слайд 8Комплексные числа

Определение 1. Числа вида a + bi,

где a и b – действительные числа,
i – мнимая единица,
называются комплексными.

a - действительная часть комплексного числа,
bi – мнимая часть комплексного числа,
b – коэффициентом при мнимой части.

Слайд 9VII в.н.э.-
квадратный корень из положительного числа имеет два значения – положительное

и отрицательное, а из отрицательных чисел квадратные корни извлечь нельзя: нет такого числа х, чтобы
х2 = -9.

Слайд 10В XVI веке
в связи с изучением
кубических уравнений
оказалось необходимым
извлекать квадратные

корни
из отрицательных чисел.
Первым учёным,
предложившим ввести
числа новой природы,
был Джорж Кордано.

Слайд 11Он предложил

Кордано назвал такие величины
“чисто отрицательными” или даже “софистически отрицательными”, считая их бесполезными и стремился не применять их.

Слайд 12в 1572
году
итальянский учёный
Бомбелли
выпустил книгу, в

которой были
установлены первые правила
арифметических операций над
комплексными числами,
вплоть до извлечения из них
кубических корней.

Слайд 13 Название “мнимые числа” ввёл французский математик

и философ Р. Декарт

в 1637
году

Слайд 14 один из крупнейших математиков XVIII века – Л. Эйлер

предложил использовать первую букву французского слова imaginare (мнимый) для обозначения

в 1777
году

Слайд 15
гораздо
В настоящее время
в математике
шире,
комплексные числа
используются
действительные
чем

Слайд 16Комплексные
числа имеют
прикладное значение
во многих областях науки, являются
основным

аппаратом
для расчетов
в электротехнике и связи.

Слайд 17Применяются при конструировании ракет

и самолетов

Слайд 18При вычерчивании географических карт

Слайд 19В исследовании

течения воды, а также во многих других науках.

Слайд 20a + bi = c + di, если a

= c и b = d.

Определение 2.

Слайд 21Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x

= – 7. Отсюда

Найти x и y из равенства: 3y + 5xi = 15 – 7i;

Пример .

Слайд 22(а+bi)

Вычитание

=(a+c)
+
(c+di)
Сложение
(b+d)
+
i
(а+bi)
-
(c+di)
=(a-c)
+
(b-d)
i

Слайд 23Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.

Найти: а) z1 + z2; б) z1 – z2;

а) z1 + z2 =(2 + 3i) + (5 – 7i) =
=(2 + 5) + (3i – 7i) = 7 – 4i;

б) z1 – z2 =(2 + 3i) – (5 – 7i) =
=(2 – 5) + (3i + 7i) = – 3 + 10i;

Решение.

Слайд 24Умножение
(c+di)
= ac
bс
i
=

+
+
+
аd
bd
(а+bi)
i

=
=
(ac-bd)
+
(аd+bc)
i
i2

Слайд 25Выполните действия:
(5 + 3i)(5 – 3i)
(2 + 3i)(5 –

7i)

(2 – 7i)2

(10+21) + (-14+15)i

31+i

25-9i2

4 - 28i + 49i2

-45-28i

25m2+16

(5m-4i)(5m+4i)

25m2 -16i2

Слайд 26Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг

от друга только знаками перед мнимой частью. z1= a+bi и z2=a-bi

Слайд 27Деление

=
=

=

Слайд 28Выполните действия:

=

=
=
2

Слайд 29Домашняя работа

2) Найти x и y из равенства:
(2x +

3y) + (x – y)i = 7 + 6i.

1) (i63+i17+i13+i82)(i72–i34);

Скачать презентацию

Вычислите: презентация

Содержание

Слайд 1Вычислите:

Слайд 2Мнимая единица
i – начальная буква французского слова

Слайд 3Например,

Вычислите:

Слайд 4

Слайд 5
Значения степеней числа i
повторяются с периодом,

Слайд 6
Решение.
i ,– 1, – i ,

Слайд 7Вычислите:

-1
-i
1
2-i
-1

Слайд 8Комплексные числа

Определение 1. Числа вида a + bi,

Слайд 9VII в.н.э.-
квадратный корень из положительного числа имеет два значения – положительное

Слайд 10В XVI веке
в связи с изучением
кубических уравнений
оказалось необходимым
извлекать квадратные

Слайд 11Он предложил

Слайд 12в 1572
году
итальянский учёный
Бомбелли
выпустил книгу, в

Слайд 13 Название “мнимые числа” ввёл французский математик

Слайд 14 один из крупнейших математиков XVIII века – Л. Эйлер

Слайд 15
гораздо
В настоящее время
в математике
шире,
комплексные числа
используются
действительные
чем

Слайд 16Комплексные
числа имеют
прикладное значение
во многих областях науки, являются
основным

Слайд 17Применяются при конструировании ракет

Слайд 18При вычерчивании географических карт

Слайд 19В исследовании

Слайд 20a + bi = c + di, если a

Слайд 21Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x

Слайд 22(а+bi)

Вычитание

=(a+c)
+
(c+di)
Сложение
(b+d)
+
i
(а+bi)
-
(c+di)
=(a-c)
+
(b-d)
i

Слайд 23Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.

Слайд 24Умножение
(c+di)
= ac
bс
i
=

+
+
+
аd
bd
(а+bi)
i

=
=
(ac-bd)
+
(аd+bc)
i
i2

Слайд 25Выполните действия:
(5 + 3i)(5 – 3i)
(2 + 3i)(5 –

Слайд 26Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг

Слайд 27Деление

=
=

=

Слайд 28Выполните действия:

=

=
=
2

Слайд 29Домашняя работа

2) Найти x и y из равенства:
(2x +

Обратная связь

Что такое ThePresentation.ru?

Вычислите: презентация

Содержание

Слайд 1Вычислите:

Слайд 2Мнимая единицаi – начальная буква французского слова

Слайд 3Например,Вычислите:

Слайд 4

Слайд 5Значения степеней числа i повторяются с периодом,

Слайд 6 Решение. i ,– 1, – i ,

Слайд 7Вычислите:-1-i 1 2-i -1

Слайд 8Комплексные числа Определение 1. Числа вида a + bi,

Слайд 9VII в.н.э.-квадратный корень из положительного числа имеет два значения – положительное

Слайд 10В XVI векев связи с изучением кубических уравнений оказалось необходимымизвлекать квадратные

Слайд 11Он предложил

Слайд 12в 1572 году итальянский учёный Бомбелли выпустил книгу, в

Слайд 13 Название “мнимые числа” ввёл французский математик

Слайд 14 один из крупнейших математиков XVIII века – Л. Эйлер

Слайд 15гораздоВ настоящее время в математикешире,комплексные числаиспользуются действительные чем

Слайд 16Комплексные числа имеют прикладное значение во многих областях науки, являются основным

Слайд 17Применяются при конструировании ракет

Слайд 18При вычерчивании географических карт

Слайд 19В исследовании

Слайд 20a + bi = c + di, если a

Слайд 21Решение. Согласно условию равенства комплексных чисел имеем 3y = 15, 5x

Слайд 22(а+bi) Вычитание=(a+c)+(c+di)Сложение(b+d)+i(а+bi)-(c+di)=(a-c)+(b-d)i

Слайд 23Выполните действия:z1 = 2 + 3i, z2 = 5 – 7i.

Слайд 24Умножение(c+di)= acbсi=+++аdbd(а+bi)i==(ac-bd)+(аd+bc)ii2

Слайд 25Выполните действия: (5 + 3i)(5 – 3i) (2 + 3i)(5 –

Слайд 26Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг

Слайд 27Деление===

Слайд 28Выполните действия:===2

Слайд 29Домашняя работа 2) Найти x и y из равенства: (2x +

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 2Мнимая единица
i – начальная буква французского слова

Слайд 3Например,

Вычислите:

Слайд 5
Значения степеней числа i
повторяются с периодом,

Слайд 6
Решение.
i ,– 1, – i ,

Слайд 7Вычислите:

-1
-i
1
2-i
-1

Слайд 8Комплексные числа

Определение 1. Числа вида a + bi,

Слайд 9VII в.н.э.-
квадратный корень из положительного числа имеет два значения – положительное

Слайд 10В XVI веке
в связи с изучением
кубических уравнений
оказалось необходимым
извлекать квадратные

Слайд 12в 1572
году
итальянский учёный
Бомбелли
выпустил книгу, в

Слайд 15
гораздо
В настоящее время
в математике
шире,
комплексные числа
используются
действительные
чем

Слайд 16Комплексные
числа имеют
прикладное значение
во многих областях науки, являются
основным

Слайд 22(а+bi)

Вычитание

=(a+c)
+
(c+di)
Сложение
(b+d)
+
i
(а+bi)
-
(c+di)
=(a-c)
+
(b-d)
i

Слайд 23Выполните действия:
z1 = 2 + 3i, z2 = 5 – 7i.

Слайд 24Умножение
(c+di)
= ac
bс
i
=

+
+
+
аd
bd
(а+bi)
i

=
=
(ac-bd)
+
(аd+bc)
i
i2

Слайд 25Выполните действия:
(5 + 3i)(5 – 3i)
(2 + 3i)(5 –

Слайд 27Деление

=
=

=

Слайд 28Выполните действия:

=

=
=
2

Слайд 29Домашняя работа

2) Найти x и y из равенства:
(2x +