- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Волновые свойства микрочастиц презентация
Содержание
- 1. Волновые свойства микрочастиц
- 2. Волновое движение носит разнообразный характер и весьма
- 3. Но на рубеже XIX и XX
- 4. Электромагнитное излучение характеризуется волновым вектором k
- 5. В результате корпускулярная интерпретация формулы (1)
- 6. Физика в своем развитии часто встречалась с
- 7. Гипотеза де Бройля Такая двойственность теории
- 8. Волна-частица обладает энергией и импульсом. Де
- 9. В 1923 году в одном из своих
- 11. Первый эксперимент осуществили в 1927 г. американские
- 12. Были воспроизведены с дополнениями условия опыта, поставленного
- 13. Дифракция на щели Дифракция на щели
- 15. Эрвин Шрёдингер Erwin Rudolf Josef Alexander
- 16. Уравнение Шредингера не выводится строго, но его
- 17. Теперь уравнение
- 18. Это и есть волновое уравнение
- 19. Это уравнение получило название нестационарного
- 20. Используем это решение
- 21. Из указанных вариантов нестационарное уравнение является универсальным
- 22. Шредингер полагал, что в волновой механике «…обычные
- 23. Первая статья называлась "Квантование как задача о
- 24. Принцип неопределенности Гейзенберга В 1927 годы
- 26. Теперь рассмотрим
- 27. Последний результат обобщен Гейзенбергом и сформулирован как
- 28. Волны вероятности, введенные М. Борном, поссорили
- 29. В классической механике предполагается, что человек
- 30. Принцип неопределённости указывает на то, что
- 31. Квантовая теория - единственная физическая теория,
- 32. Осенью 1926 г. Шредингер приехал по приглашению
- 33. Шрёдингер полагал, что частицы можно наглядно
- 34. «Шредингер был,
- 35. Члены международной научной группы под общим руководством
- 36. Атом находится в электрическом поле Е и
- 37. Члены международной научной группы под общим руководством
Слайд 2Волновое движение носит разнообразный характер и весьма распространено в природе.
Любая
До конца XIX в. считалось, что излучение имеет чисто волновую природу. Правда, гипотеза о корпускулярном строении света высказывалась ранее неоднократно. Её разделял, например, Ньютон. Однако, после исследований Френеля и Юнга в начале XIX в. по интерференции и дифракции световых волн и, особенно, после создания Максвеллом электродинамики во второй половине XIX в. возобладала волновая концепция.
Слайд 3
Но на рубеже XIX и XX вв. появились факты, свидетельствующие в
В 1900 г. Планк в основу теории чёрного тела положил гипотезу о квантованных осцилляторах. Он предположил, что стенки полости обмениваются энергией с полем излучения, причём порции энергии не могут быть меньше, чем ħω, где ω — собственная частота осциллятора.
Позднее, в 1905 г. Эйнштейн предложил объяснение фотоэффекта, в котором квантовые свойства имеет уже само излучение, а не только гипотетические осцилляторы полости.
Слайд 4
Электромагнитное излучение характеризуется волновым вектором k и частотой ω. Описание плоской
где ψ— любая величина, принимающая участие в волновом движении, а ψ0 — её амплитуда
По Планку энергия кванта (фотона) связана с частотой волны:
а его импульс — с её волновым вектором:
Слайд 5
В результате корпускулярная интерпретация формулы (1)
выглядит следующим образом:
В этом
Слайд 6Физика в своем развитии часто встречалась с границами применимости существующих теорий.
Совсем по-другому сложились взаимоотношения волновой и квантовой оптики. Ни одна из них не стала частью другой. Остались задачи (дифракция, интерференция, поляризация электромагнитных волн) которые решаются в рамках только волновой теории излучения. С другой стороны, были обнаружены явления (фотоэффект, эффект Комптона, “ультрафиолетовая катастрофа” в теории Рэлея-Джинса теплового излучения), которые объясняются только корпускулярной природой света.
Как пошутил Уильям Брэгг, «сложилась ситуация, когда каждый физик вынужден по понедельникам, средам и пятницам считать свет состоящим из частиц, а в остальные дни – из волны».
Слайд 7Гипотеза де Бройля
Такая двойственность теории излучения – корпускулярно-волновой дуализм света привела
Если волна – частица, то и материальная частица – волна.
Он показал, что движению электрона может соответствовать некоторая волна материи, так же как движению светового кванта соответствует световая волна. Де Бройль предложил объяснить квантовые условия теории Бора с помощью представления о волнах материи. Волна, движущаяся вокруг ядра атома, по геометрическим соображениям может быть только стационарной волной; длина орбиты должна быть кратной целому числу длин волн.
Слайд 8
Волна-частица обладает энергией и импульсом. Де Бройль назвал ее “фазовой волной”.
Волны Де Бройля для электрона с n = 2, 3, 4
Слайд 9В 1923 году в одном из своих докладов Парижской Академии наук
«Поток электронов, проходя через узкую щель, должен был бы дать явление дифракции»
Однако первое подтверждение справедливости волновой механики было получено в опытах по интерференции электронов.
Слайд 10
Пучок ускоренных электронов падает на экран с двумя узкими щелями. Если закрыть одну щель, то электроны, прошедшие через другую, дадут определенное распределение интенсивности. Подобное же распределение, но несколько смещенное будет получено, если закрыть вторую щель и открыть первую. Теперь оставим открытыми обе щели. Здравый смысл подсказывает, что новое распределение частиц должно равняться сумме первых двух (распределение 1). Однако опыт свидетельствует совсем о другом ( распределение 2).
Распределение электронов отвечает интерференции двух когерентных волн. Таким образом, на движение каждого отдельного электрона оказывают влияние обе щели. Этот эксперимент подтверждает тот факт, что микрочастица-волна не просто «маленькое» материальное тело.
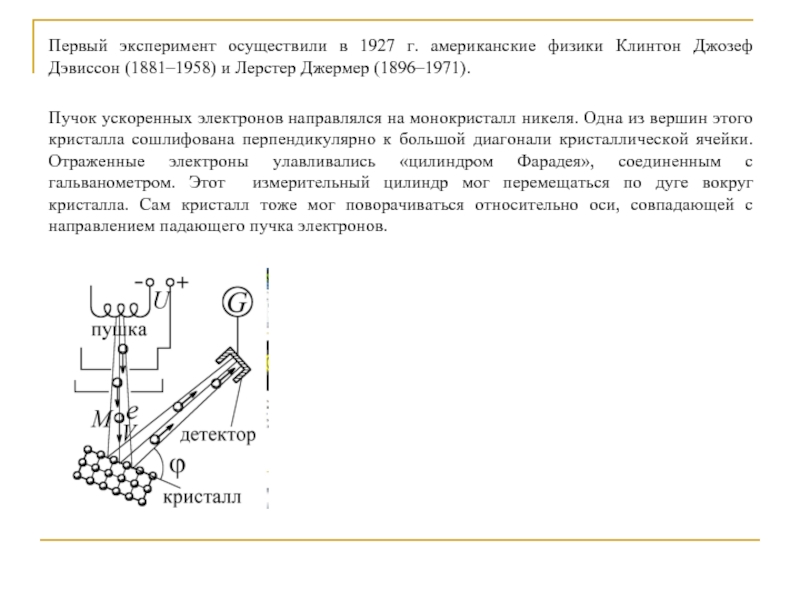
Слайд 11Первый эксперимент осуществили в 1927 г. американские физики Клинтон Джозеф Дэвиссон
Пучок ускоренных электронов направлялся на монокристалл никеля. Одна из вершин этого кристалла сошлифована перпендикулярно к большой диагонали кристаллической ячейки. Отраженные электроны улавливались «цилиндром Фарадея», соединенным с гальванометром. Этот измерительный цилиндр мог перемещаться по дуге вокруг кристалла. Сам кристалл тоже мог поворачиваться относительно оси, совпадающей с направлением падающего пучка электронов.
Слайд 12Были воспроизведены с дополнениями условия опыта, поставленного Дэвиссоном еще в 1921
Расстояние между атомными плоскостями монокристалла никеля – d было известно из рентгенографических исследований. Сила тока рассеянных электронов оказалась максимальной при определенном значении угла рассеяния θ. Длина волны, соответствующая этому интерференционному максимуму, оказалась равной
d cosθ = m λ ⇒ λ = 1.65 Å.
В то же время легко рассчитать длину волны де-Бройля падающих электронов
λ = 2πh / p = 2πh /(mv) =1.65A,
где v = 2eU m — скорость электронов при ускоряющем напряжении U = 54 В.
Совпадение этих длин волн и явилось первым подтверждением волновых свойств частиц – в данном случае электронов.
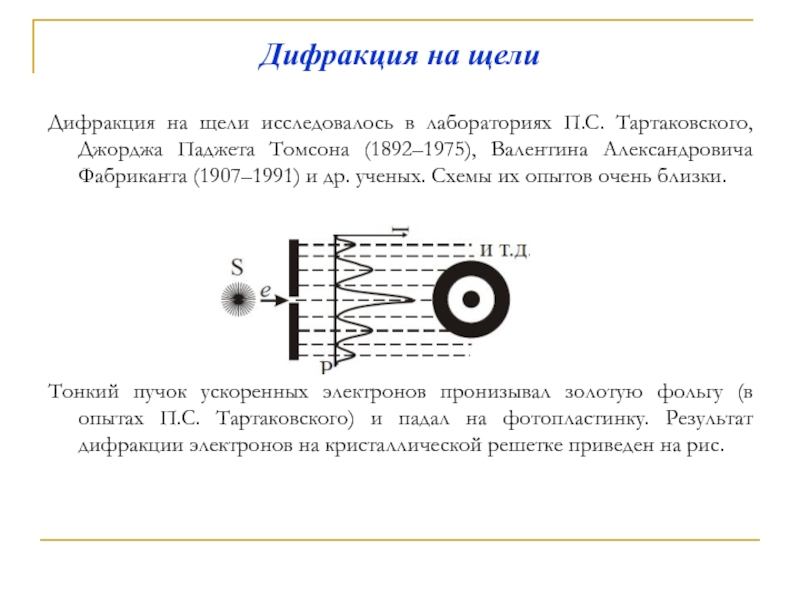
Слайд 13Дифракция на щели
Дифракция на щели исследовалось в лабораториях П.С. Тартаковского, Джорджа
Тонкий пучок ускоренных электронов пронизывал золотую фольгу (в опытах П.С. Тартаковского) и падал на фотопластинку. Результат дифракции электронов на кристаллической решетке приведен на рис.
Слайд 14 Уравнение Шредингера
При решении задачи построения физических теорий, объясняющих некоторые экспериментальные факты, обычно сначала выдвигается физическая идея, объясняющая явление качественно, «на пальцах». Затем идея проверяется на количественное согласие с экспериментом, если ее удается корректно представить в понятиях математики. В этой процедуре все величины, входящие в уравнения, получают свое истолкование на стадии составления уравнений, поэтому проблем с интерпретацией их физического смысла не возникает.
В ряде случаев, однако, за неимением иной возможности, поступают противоположным образом. Сначала, после ряда математических операций, добывают результат, а затем решают вопрос физического смысла входящих в решение уравнения величин. Так было в случае с уравнениями Максвелла, преобразованиями Лорентца, соотношением неопределенности, так было и с уравнением Шредингера.
Слайд 15Эрвин Шрёдингер
Erwin Rudolf Josef Alexander Schrödinger
(1887—1961)
Австрийский физик-теоретик, один из создателей
Лауреат Нобелевской премии по физике (1933).
Шрёдингеру принадлежит ряд фундаментальных результатов в области квантовой теории, которые легли в основу волновой механики: он сформулировал волновые уравнения (стационарное и зависящее от времени уравнения Шрёдингера), показал тождественность развитого им формализма и матричной механики, разработал волновомеханическую теорию возмущений, получил решения ряда конкретных задач.
Шрёдингер предложил оригинальную трактовку физического смысла волновой функции; в последующие годы неоднократно подвергал критике общепринятую копенгагенскую интерпретацию квантовой механики (парадокс «кота Шрёдингера» и прочее).
Кроме того, он является автором множества работ в различных областях физики: статистической механике и термодинамике, физике диэлектриков, теории цвета, электродинамике, общей теории относительности и космологии; он предпринял несколько попыток построения единой теории поля. В книге «Что такое жизнь?» Шрёдингер обратился к проблемам генетики, взглянув на феномен жизни с точки зрения физики. Он уделял большое внимание философским аспектам науки, античным и восточным философским концепциям, вопросам этики и религии.
Слайд 16Уравнение Шредингера не выводится строго, но его можно получить из так
Согласно гипотезе де Бройля, каждой движущейся микрочастице должна быть сопоставлена волна.
Пусть свободной микрочастице, летящей вдоль оси x, cоответствует плоская волна.
Свяжем параметры волны с энергией и импульсом микрочастицы
Слайд 17Теперь уравнение
Продифференцируем это выражение один раз по времени и дважды – по координате:
В случае свободного движения нерелятивистской частицы, ее энергия и импульс связаны простым соотношением E=p2/2m. Теперь, принимая во внимание это соотношение, легко связать предыдущие уравнения
Слайд 18
Это и есть волновое уравнение Шредингера для одномерного движения свободной частицы.
В
получим:
Это уравнение Шредингера для одномерного движения микрочастицы в силовом поле. Для частицы, движущейся в произвольном направлении, запишем волновое уравнение в таком виде:
Слайд 19
Это уравнение получило название нестационарного волнового уравнение Шредингера . Здесь
При движении
Слайд 20Используем это решение
Сократив на общий множитель exp[−i(E/h)t], получим УШ для стационарных состояний
Слайд 21Из указанных вариантов нестационарное уравнение является универсальным
Шрёдингер ввел греческую букву ψ
Однако в общем случае функция ψ в общем случае комплекснозначная, и поэтому было трудно понять, каков ее физический смысл.
Слайд 22Шредингер полагал, что в волновой механике «…обычные правила квантования могут быть
То есть самым существенным Шредингеру кажется то, что он смог описать таинственные квантовые явления методами, характерными для сугубо классической физики того времени.
"Не требует особых разъяснений то обстоятельство, что представление, по которому при квантовом переходе энергия преобразуется из одной колебательной формы в другую значительно более удовлетворительно, чем представление о перескакивающем электроне. Изменение формы колебаний всегда может происходить непрерывно в пространстве и времени, оно может длиться время, равное определяемому экспериментально времени процесса излучения...".
Основополагающая серия работ в журнале «Annalen der Physik» с 27 января по 21 июня 1926 года.
Слайд 23Первая статья называлась "Квантование как задача о собственных значениях" ("Quantisierung als
Спустя 35 лет Макс Борн писал: "Что существует более выдающегося в теоретической физике, чем его первые шесть работ по волновой механике?"
В "первые шесть работ" Шредингера, входят четыре статьи под общим названием "Квантование как задача о собственных значениях", работа "Об отношении квантовой механики Гейзенберга-Борна-Иордана к моей", в которой показана математическая эквивалентность матричной и волновой механик, и работа "Непрерывный переход от микро- к макромеханике" - самая слабая в цикле, но сильно повлиявшая на взгляды самого Шредингера, который почти до конца своей жизни пытался строить компактные волновые пакеты, которые бы соответствовали движению микрочастиц, так как это впервые было им проделано в "Непрерывном переходе..." для частного случая потенциала гармонического осцилятора.
Основные работы Э.Шредингера переведены на русский язык
Слайд 24Принцип неопределенности Гейзенберга
В 1927 годы Гейзенберг и его научный руководитель Макс
М. Борну было 44 года, он был на три года старше Бора и на два года младше Эйнштейна. (Гейзенбергу было 25 лет).
Иными словами Борн и Гейзенберг предполагают существование частицы и связанной с ней непрерывной волны Ψ, но частица не имеет ни определённой скорости, ни определённой траектории. Речь может идти лишь о вероятности нахождения частицы в той или иной области пространства.
Слайд 25
Поток микрочастиц подлетает к экрану
Достоверно известно, что перед щелью х-компонента импульса микрочастицы рx = 0. Здесь скорость частиц перпендикулярна экрану, т.е. оси x. Погрешность этого сведения Δрx = 0. Однако при этом совершенно не определена х-координата частицы.
Слайд 26
Теперь рассмотрим движение частицы-волны за щелью Δх. За щелью дифрагировавшие частицы
Кроме того, теперь в щели мы можем указать х-координату с погрешностью Δx . Тогда Δpx = 2πh / Δx или Δp ⋅Δx = 2πh = h .
Слайд 27Последний результат обобщен Гейзенбергом и сформулирован как один из основных принципов
ΔA⋅ΔB ≥ h
Сопряженными величинами являются координаты и соответствующие проекции импульса, энергия и время. Произведение неопределенностей этих величин не может быть меньше по порядку величины постоянной Планка ħ , т.е.
Последнее соотношение означает, что чем точнее мы хотели бы измерить энергию частицы, тем большее время займет это измерение.
Слайд 28
Волны вероятности, введенные М. Борном, поссорили его с Гейзенбергом, который обвинил
Бор отнесся к представлениям Борна с пониманием, он был убежден, что глубины материи - мир вероятностных закономерностей.
Гейзенберг не оспаривал этого, он был возмущен тем, что М. Борн в своем исследовании опирался на волновую механику Шредингера, а не на матричную механику.
Слайд 29
В классической механике предполагается, что человек может наблюдать явление, не нарушая
В микромире дело обстоит иначе. Например, исследуя движение электрона с помощью микроскопа (если бы такое было возможно), мы бы наблюдали отраженные от электрона волны света, энергия которых по величине сопоставима с энергией самих исследуемых частиц. Поэтому при выполнении измерений нами неизбежно вносились бы изменения в состояние электрона (местоположение, скорость, направление движения и т.д.). Значит, на основании наших измерений бессмысленно говорить о точном местоположении электрона в каждый момент времени.
Слайд 30
Принцип неопределённости указывает на то, что частицы могут вести себя как
Таким образом, квантовая механика фиксирует корпускулярно-волновой дуализм – в одних случаях удобнее частицы считать волнами, в других, наоборот, волны частицами.
С принципом неопределённости поначалу соглашались далеко не все физики; его всеобщему признанию предшествовала довольно длительная дискуссия. Осуществлённая Гейзенбергом и развитая Бором интерпретация квантовой теории получила название копенгагенской, названной так по месту жительства основателя этой школы Нильса Бора.
Слайд 31
Квантовая теория - единственная физическая теория, которая имеет не одну, а
Копенгагенская интерпретация предполагает, с одной стороны, описание экспериментов в понятиях классической физики, а с другой - признание этих понятий неточно соответствующими действительному положению вещей. В рамках данной интерпретации основным положением квантовой теории выступает принцип дополнительности, означающий требование применять для получения в процессе познания целостной картины изучаемого объекта взаимоисключающие классы понятий, приборов и исследовательских процедур, которые используются в своих специфических условиях и взаимозаполняют друг друга.
Слайд 32Осенью 1926 г. Шредингер приехал по приглашению Бора в Копенгаген. Гейзенберг
Он лежал больной в институтской квартире Бора, дискуссии не прекращались. Бор часто повторял: "Но, Шредингер, Вы все-таки должны согласиться…" А Шредингер не соглашался. Бор (в пересказе Гейзенберга): "То, что Вы говорите, абсолютно правильно. Но это не доказывает, что квантовых скачков нет. Это означает, что мы не можем их вообразить, что предметно-изобразительные представления, с помощью которых мы описываем события повседневной жизни и эксперименты классической физики, становятся непригодными, когда мы переходим к описанию квантовой прерывности".
На что Шредингер заявил, что формулирование представления о природе его вообще не интересует: "Я предпочитаю оставить это философам". Это было пренебрежение к философско-физическим размышлениям Бора, и Бор превратился, по словам Гейзенберга, в "почти лишенного милосердия фанатика".
Бор всегда не мог дождаться, когда проснется больной Шредингер, и будил его для продолжения дискуссий. В конце концов, изнуренный Шредингер заявил: "Если эти проклятые квантовые скачки сохранятся в физике, я простить себе не смогу, что вообще связался с квантовой теорией!"
Слайд 33
Шрёдингер полагал, что частицы можно наглядно представлять как волновые пакеты, должным
Невозможность этого обяснялась современными ему учеными: в общем случае волновые пакеты неизбежно расплываются, что находится в противоречии с явно корпускулярным поведением частиц в экспериментах по рассеянию электронов.
Решение проблемы данное Максом Борном, предложившим вероятностную интерпретацию волновой функции, была для него абсолютно неприемлема
Слайд 34
«Шредингер был, по меньшей мере, столь же, как
М. Борн
Высказывание Шредингера, сделанное им уже в преклонном возрасте – в 1957 году:
«Я хочу ясно сказать, что отныне и впредь беру на себя всю ответственность за свое упрямство. Я иду против течения, но направление потока изменится»
Слайд 35Члены международной научной группы под общим руководством Анеты Стодольна из лаборатории
Внутри закрытой камеры устанавливаются два лазера, между которыми помещается атом водорода. Лазеры начинают обстреливать этот атом, в результате чего электрон вылетает из него со скоростью и в направления и, которые зависят от его волновой функции излучения. Если в камере не один, а несколько атомов, то те, соответственно, выпустят несколько электронов, которые будут интерферировать.
Отделившиеся электроны направляются на чувствительную матрицу через положительно заряженное кольцо, причем положение электрона в момент столкновения с матрицей отражает положение электрона в момент ионизации атома. Заряженное кольцо, отклоняющее электроны в сторону, играет роль линзы и с его помощью изображение увеличивается в 20 тысяч раз.
Слайд 36Атом находится в электрическом поле Е и возбуждается лазерными импульсами (показанных
Hydrogen Atoms under Magnification: Direct Observation ofHydrogen Atoms under Magnification: Direct Observation of Hydrogen Atoms under Magnification: Direct Observation of the Nodal Structure of Stark States
A. S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H.A. S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. A. S. Stodolna, A. Rouzée, F. Lépine, S. Cohen, F. Robicheaux, A. Gijsbertsen, J. H. Jungmann, C. Bordas, and M. J. J. Vrakking
Слайд 37Члены международной научной группы под общим руководством Анеты Стодольна из лаборатории
Внутри закрытой камеры устанавливаются два лазера, между которыми помещается атом водорода. Лазеры начинают обстреливать этот атом, в результате чего электрон вылетает из него со скоростью и в направления и, которые зависят от его волновой функции излучения. Если в камере не один, а несколько атомов, то те, соответственно, выпустят несколько электронов, которые будут интерферировать.
Размер фотографии 4 на 4 мм