- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вейвлеты при анализе скважинных данных презентация
Содержание
- 1. Вейвлеты при анализе скважинных данных
- 2. План Кратномасштабный вейвлет-анализ Произвольный информационный сигнал
- 3. Вспомним про вейвлеты: Берем порождающий вейвлет (функция
- 4. НО! И непрерывное и дискретное вейвлет-преобразования с
- 5. Произвольный информационный сигнал = региональная функция
- 6. Выделение пластов Фильтрация данных Корреляция скважин и т.д.
- 7. Применение к задаче выделения пластов
- 8. Сигнал есть сумма функций, каждая из которых
- 9. Преобразование коэффициентов методом трешолдинга (кратко: применяем преобразование
- 10. Применение к задаче выделения пластов
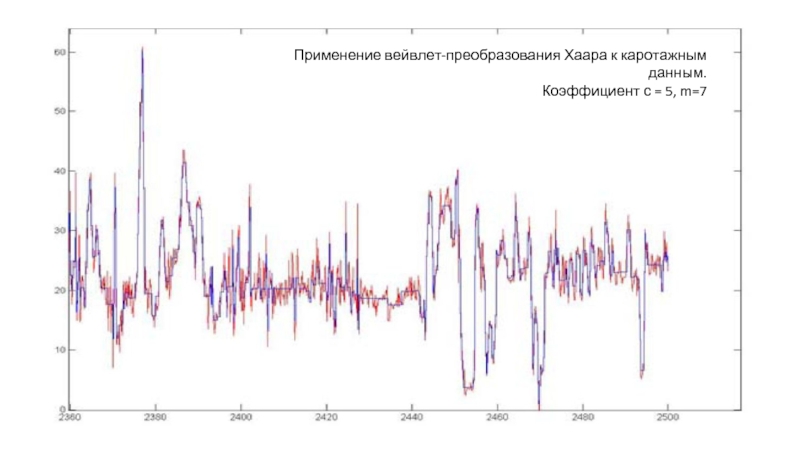
- 11. Применение вейвлет-преобразования Хаара к каротажным данным. Коэффициент с = 5, m=7
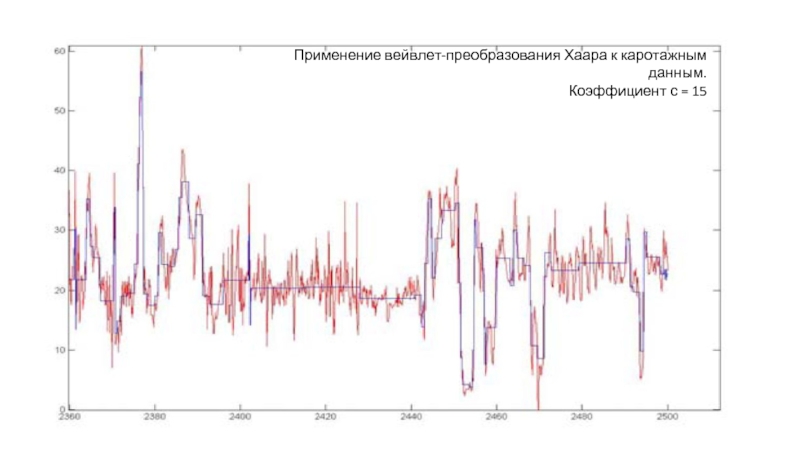
- 12. Применение вейвлет-преобразования Хаара к каротажным данным. Коэффициент с = 15
- 13. Подвергнем коэффициент dk,i’дополнительному преобразованию, которое зануляет все
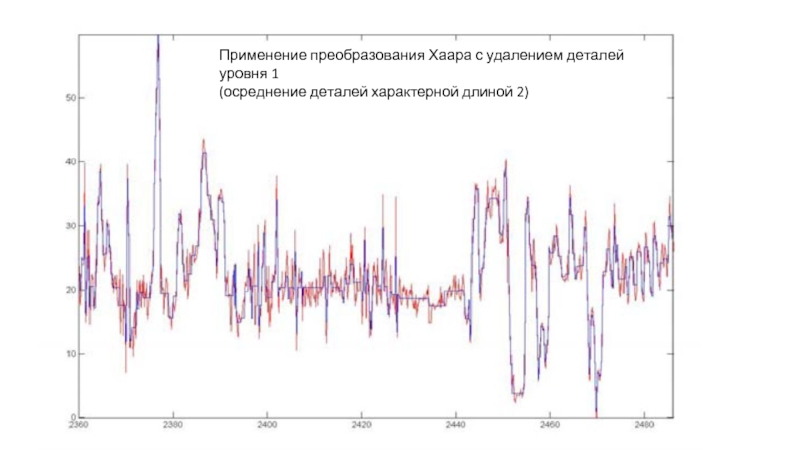
- 14. Применение преобразования Хаара с удалением деталей уровня 1 (осреднение деталей характерной длиной 2)
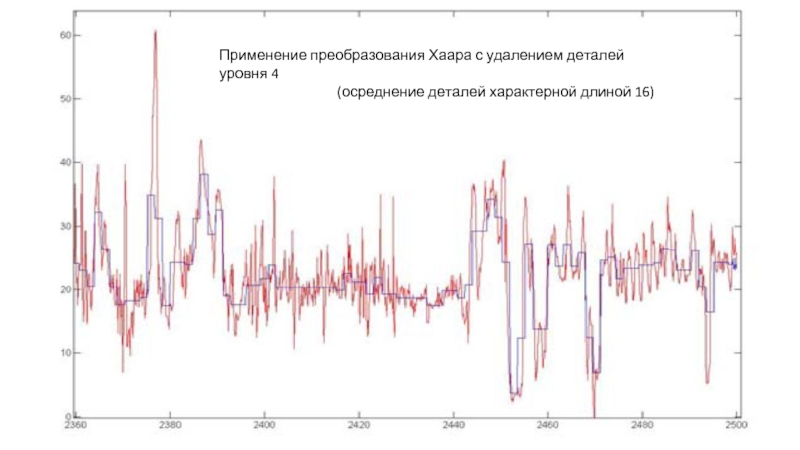
- 15. Применение преобразования Хаара с удалением деталей уровня 4 (осреднение деталей характерной длиной 16)
- 16. Выводы 1) использование вейвлет-преобразований Хаара в большинстве
- 17. Да, мы все поняли
- 18. Вопросы Основная идея кратномасштабного вейвлет-анализа Для решения
- 19. Список литературы С.С. Крайниковский, «ВЕЙВЛЕТ-ОБРАБОТКА ДАННЫХ В
Слайд 1Вейвлеты при анализе скважинных данных
Кидрасова Гульназ 410
Ни одна вещь не возникает
Анаксагор. Древнегреческий философ, IV в. до н.э.
Слайд 2План
Кратномасштабный вейвлет-анализ
Произвольный информационный сигнал
Решаемые задачи
Примеры
Выводы
Вопросы
Шестая пара
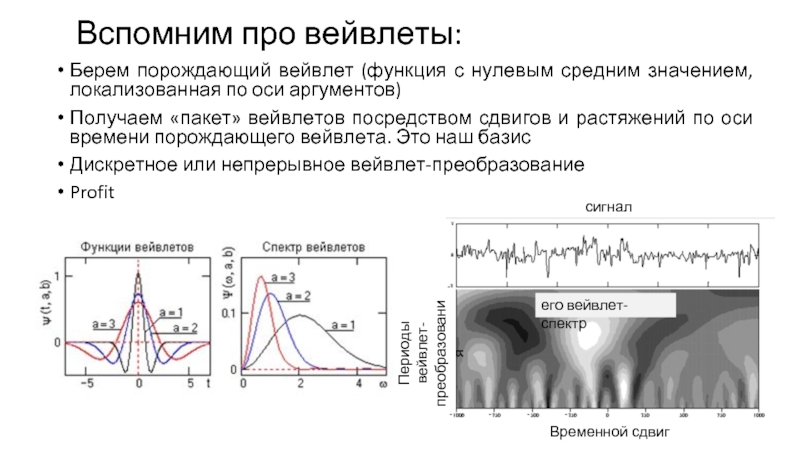
Слайд 3Вспомним про вейвлеты:
Берем порождающий вейвлет (функция с нулевым средним значением, локализованная
Получаем «пакет» вейвлетов посредством сдвигов и растяжений по оси времени порождающего вейвлета. Это наш базис
Дискретное или непрерывное вейвлет-преобразование
Profit
Периоды вейвлет-преобразования
Временной сдвиг
сигнал
его вейвлет-спектр
Слайд 4НО! И непрерывное и дискретное вейвлет-преобразования с произвольным шагом по масштабу
Достаточно знать вейвлет-преобразование на некоторой решетке частотно-временной области, густой в области высоких частот сигнала, и редкой в области низких частот. Для этого нужен кратномасштабный вейвлет-анализ (КМА).
Идея КМА - масштабировать вейвлет в постоянное число раз, и сдвигать его во времени с шагом, равным интервалу носителя масштабированного вейвлета.
Слайд 5Произвольный информационный сигнал
=
региональная функция тренда
+
циклические компоненты с определенным периодом повторения
+
локальные
флуктуации (шумы)
КМА - инструмент разделения сигнала на составляющие, анализа их порядка и реконструкции сигналов из определенных составляющих (или с исключением определенных составляющих, например шумов или малозначимых деталей)
Слайд 8Сигнал есть сумма функций, каждая из которых отражает вклад различных частотных
Основным утверждением, используемым в обработке дискретных сигналов, является существование разложения сигнала по базисным функциям разных уровней (преобразование Хаара):
Слайд 9Преобразование коэффициентов методом трешолдинга
(кратко: применяем преобразование trc к коэффициентам d, которое
Разложение сигнала по базисным функциям разных уровней
Слайд 13Подвергнем коэффициент dk,i’дополнительному преобразованию, которое зануляет все коэффициенты с индексами k
Слайд 14
Применение преобразования Хаара с удалением деталей уровня 1
(осреднение деталей характерной длиной
Слайд 15
Применение преобразования Хаара с удалением деталей уровня 4
(осреднение деталей характерной длиной
Слайд 16Выводы
1) использование вейвлет-преобразований Хаара в большинстве случаев даёт достоверную картину
2) алгоритм,
3) недостатком может являться то, что длина пласта всегда есть число, кратное 2kh , что вносит некоторую «машинную составляющую» в картину разреза. Однако для работы алгоритмов интерпретации этот фактор не является существенным, либо может быть устранён при доработке алгоритма.
Слайд 18Вопросы
Основная идея кратномасштабного вейвлет-анализа
Для решения каких задач в скважинной геофизике можно
Что такое трешолдинг коэффициентов?