- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы презентация
Содержание
- 1. Векторы
- 2. Вектором называется параллельный перенос. Для обозначения векторов
- 3. Проекцией вектора а на ось и называется
- 4. Вектор а задается координатами: а=(Ха;
- 5. Суммой векторов а; b; с называется вектор
- 6. Разность векторов а-в=АВ
- 7. Произведение вектора а на число λ
- 8. Векторы называются коллинеарными, если существует прямая, которой
- 9. Длина (модуль) вектора a = (xa; ya;
- 10. Скалярное произведение вектора а на вектор
- 11. Угол между векторами а и b определяется
- 12. Проекция вектора а на вектор b определяется
- 13. Векторное произведение векторов а и b обозначение
- 14. Формула для вычисления векторного произведения векторов а
- 15. Площадь параллелограмма, построенного на векторах а и
- 16. Смешанным произведением векторов а, b, с называется
- 17. V параллелепипеда, построенного на векторах а, b
- 18. Три вектора а, b, с называются компланарными,
- 19. Прямоугольные координаты в пространстве Если Охуz декартова
- 20. В частности, расстояние точки М (х; у;
- 21. Решение Воспользуемся формулой деления отрезка в данном
- 22. Показать, что а=2i+5j+7k;в =i+j-k; c=i+2j+2k компланарны
- 23. № 3 Найдем объем пирамиды
- 24. Задание №4 А1А2А3А4-пирамида А1(-4;-2;0) А2(-1;-2;4) А3(2;1;2) А4(3;-2;1).
- 25. 3) Найдем проекцию вектора А1А3 на вектор А1А4
- 26. Работу сделали : Ученики 11Г класса:
Слайд 2Вектором называется параллельный
перенос.
Для обозначения векторов используются символы а,b, х и т.п.
Векторы рассматриваются на плоскости
(II перенос плоскости) и в пространстве (II перенос пространства).
И в том, и другом случае вектор определяется упорядоченной парой точек, т.е. заданием точки и ее образа.
Вектор – это направленный отрезок АВ=а.
Направление луча АВ, называется направлением вектора а=АВ.
Расстояние IАВI – называется длиной или модулем а=АВ, обозначается IАВI или IаI.
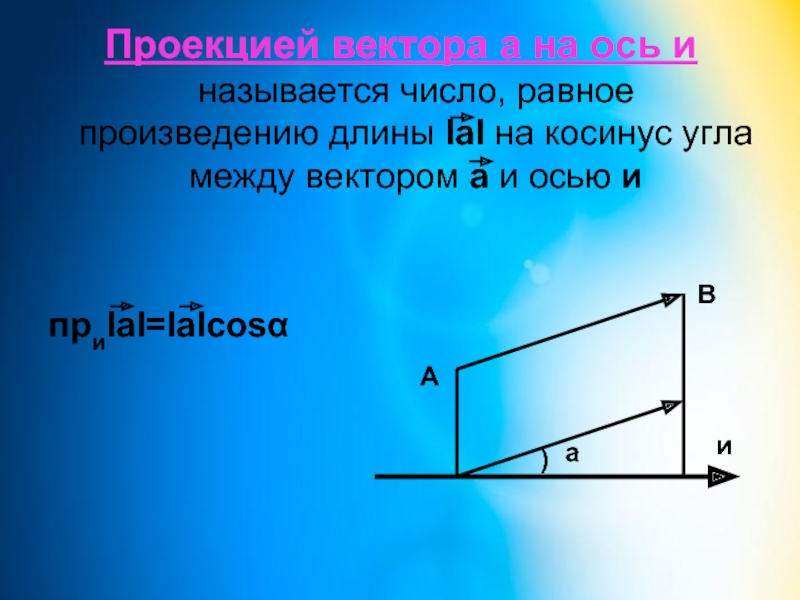
Слайд 3Проекцией вектора а на ось и называется число, равное произведению длины
приIaI=IaIcosα
Слайд 4 Вектор а задается координатами: а=(Ха; Уа; Zа), где Ха
Вектор можно задать разложением по векторам базиса i; j; k.
,где
i; j; k – единичные , т.е.
и взаимно перпендикулярные векторы.
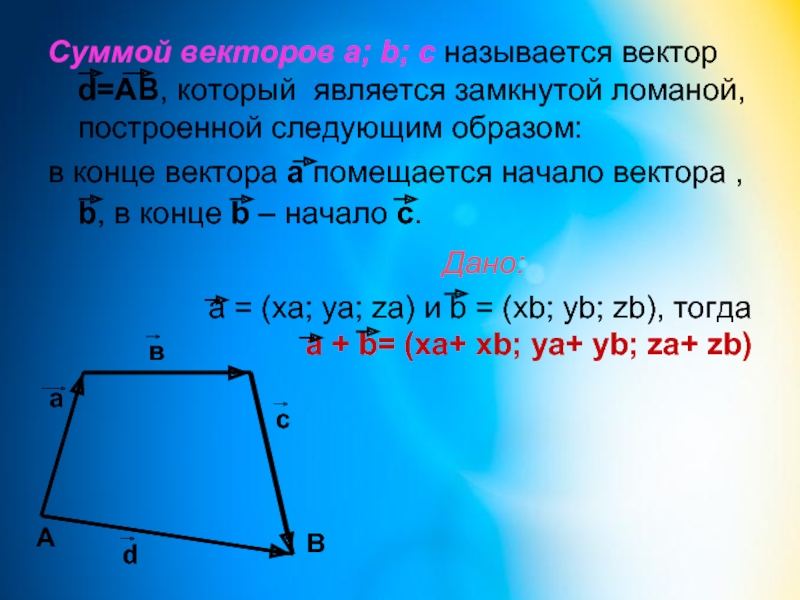
Слайд 5Суммой векторов а; b; с называется вектор d=АВ, который является замкнутой
в конце вектора а помещается начало вектора , b, в конце b – начало с.
Дано:
a = (xa; ya; za) и b = (xb; yb; zb), тогда a + b= (xa+ xb; ya+ yb; za+ zb)
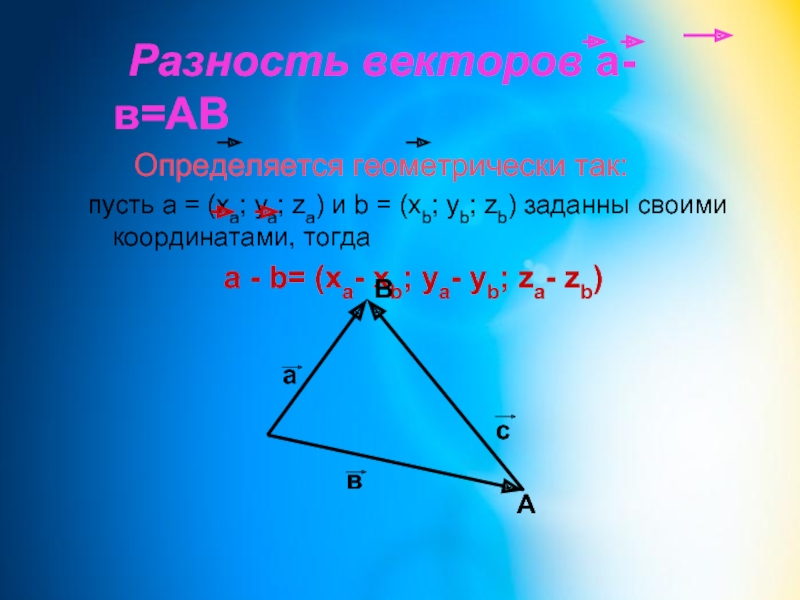
Слайд 6 Разность векторов а-в=АВ
Определяется геометрически так:
пусть a
a - b= (xa- xb; ya- yb; za- zb)
Слайд 7Произведение вектора а на число λ
Умножение вектора
λa=( λxa; λya; λza)
есть вектор с, длина которого равна IλI • IaI;
вектор с сонаправлен вектору а, если λ>0 и противоположно направлен, если λ<0.
Слайд 8Векторы называются коллинеарными, если существует прямая, которой они параллельны.
Коллинеарные векторы а
a = λb
Если известны координаты векторов, то условие коллинеарности векторов можно определить:
Слайд 9Длина (модуль) вектора a = (xa; ya; za) определяется формулой:
Если А (Х1;У1;Z1) начало и В (Х2;У2;Z2) конец
вектора АВ, то координаты АВ определяются формулой:
АВ=(Х2-Х1;У2-У1;Z2-Z1)
Слайд 10 Скалярное произведение вектора а на вектор b есть число, равное
a•b=(a,b)= IaI•IbI•cosφ
Формула для вычисления скалярного произведения векторов a = (xa; ya; za)
и b = (xb; yb; zb), заданных координатами:
a•b= xa• xb+ ya• yb+ za• zb
Слайд 11Угол между векторами а и b определяется формулой:
Если векторы a =
Слайд 12Проекция вектора а на вектор b определяется формулой:
Если векторы a =
Слайд 13Векторное произведение векторов а и b
обозначение a×b=[a,b]=[a×b] есть вектор c, удовлетворяющий
1) IcI=IaI IbI sinφ
2) c┴a и ×c┴b
3) Направление с определяется по правилу правой руки, т.е. с конца вектора с кратчайший поворот от вектора а к вектору b виден против хода часовой стрелки (правило Буравчика).
Слайд 14Формула для вычисления векторного произведения векторов а и b, заданных координатами
т.е. векторное произведение а и b – это вектор с координатами:
Слайд 15Площадь параллелограмма, построенного на векторах а и b равна модулю векторного
S= I a×b I= IaI×IbI sinφ
(φ – угол между а и b)
Площадь #, построенного на векторах, заданных координатами находится:
Слайд 16Смешанным произведением векторов а, b, с называется число, равное скалярному произведению
Формула для смешанного произведения векторов, заданных координатами:
Слайд 17V параллелепипеда, построенного на векторах а, b и с равен модулю
V пирамиды, построенной на векторах
объема параллелепипеда, построенного на этих векторах:
Слайд 18Три вектора а, b, с называются компланарными, если существует плоскость, которой
Признак компланарности трех векторов:
Три не нулевых вектора а, b, с компланарны тогда и только тогда, когда их смешанное произведение =0.
Слайд 19Прямоугольные координаты в пространстве
Если Охуz декартова система координат в пространстве, то
М (х; у; z).
Расстояние между А (х1; у1; z1) и В (х2; у2; z2) определяется:
Слайд 20В частности, расстояние точки М (х; у; z) от начала координат
Если отрезок, концами которого служат точки А (х1; у1; z1) и В (х2; у2; z2) разделен точкой С(х; у; z) в отношение λ, то координаты точки С определенности по по формуле:
В частности координаты середины отрезка определяются по формуле(т.к. λ=1)
Примечание:
Пусть на прямой заданой отрезка АВ (А начало ,В конец отрезка) Тогда всякая третья точка С этой прямой делит АВ в некотором отношении λ, где ,если АС и ВС направлены в одну строку, то λ имеет знак «+» ,если АС и ВС направлены в противоположные стороны, то λ имеет знак «-».
Слайд 21Решение
Воспользуемся формулой деления отрезка в данном отношении:
Yм =4 Z
№1
Дано:
М1(2;4;-2)
М2(-2;4;2)
На прямой М1М2
Найти М, делящую отрезок М1М2 в отношение λ=3
Слайд 23№ 3 Найдем объем пирамиды с вершинами А(2;2;2) В(4;3;3)
Решение :
Найти векторы АВ ; АС и АD совпадают с ребрами пирамиды, сходящимися в вершине А. АВ= 2i+j+k ; АС= 2i+3j+2k ; АD= 3i+3j+4k .
Слайд 24Задание №4
А1А2А3А4-пирамида А1(-4;-2;0) А2(-1;-2;4) А3(2;1;2) А4(3;-2;1).
Найти: 1) А1А2 длину ребра
2) Угол









![Векторное произведение векторов а и bобозначение a×b=[a,b]=[a×b] есть вектор c, удовлетворяющий условиям:1) IcI=IaI IbI sinφ2)](/img/tmb/1/19747/fbd93e713b51ca1b4224425d8375e66e-800x.jpg)


















