- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Устойчивость систем нелинейных дифференциальных уравнений презентация
Содержание
- 1. Устойчивость систем нелинейных дифференциальных уравнений
- 2. Цель работы Целью данной курсовой
- 3. Постановка задачи На основе изученного
- 4. Введение Анализ
- 5. Целочисленный пример Рассматриваемая система дифференциальных уравнений является
- 6. Для обработки данного примера
- 7. Затем при помощи макроса мы расшатываем начальные
- 8. Рисунок 1. Графики зависимости математического ожидания и
- 9. Рисунок 2. Графики зависимости математического ожидания и
- 10. Рисунок 3. Графики зависимости математического ожидания и
- 11. Рисунок 4. Графики зависимости математического ожидания и
- 12. Рисунок 5. Графики зависимости математического ожидания и
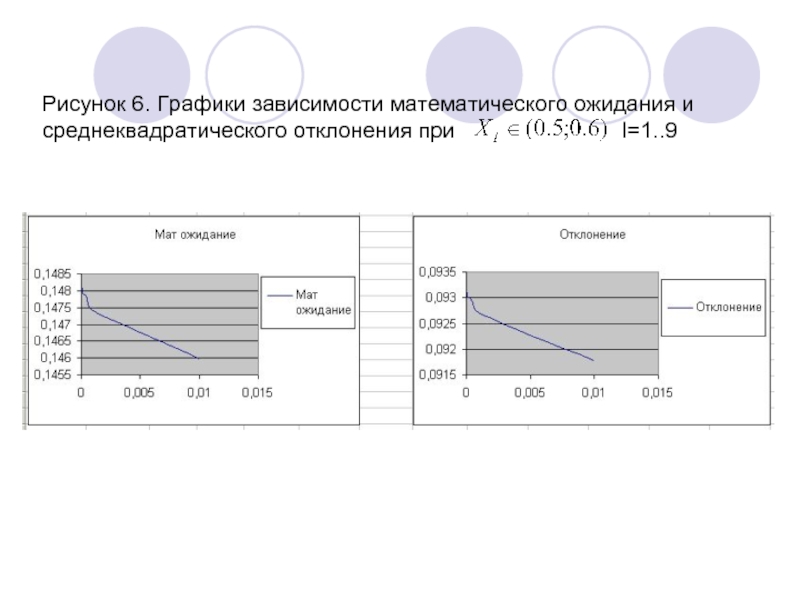
- 13. Рисунок 6. Графики зависимости математического ожидания и
- 14. Рисунок 7. Графики зависимости математического ожидания и
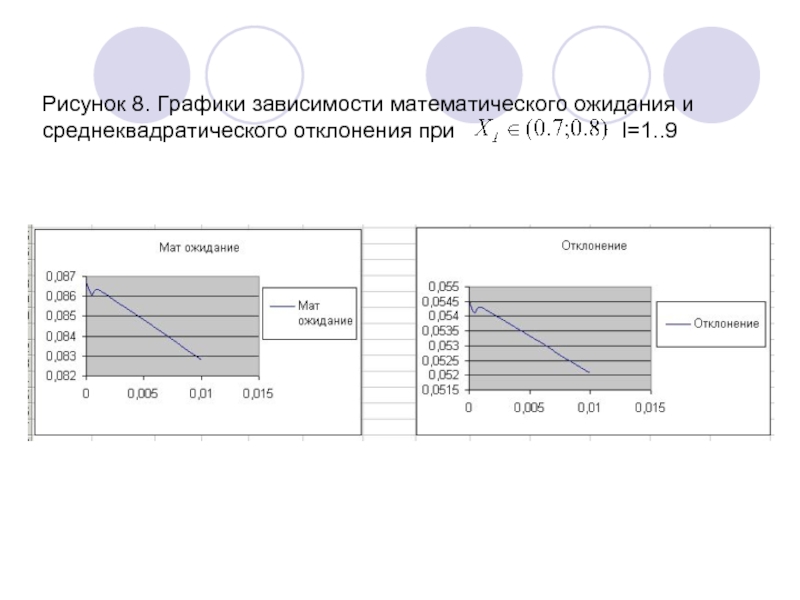
- 15. Рисунок 8. Графики зависимости математического ожидания и
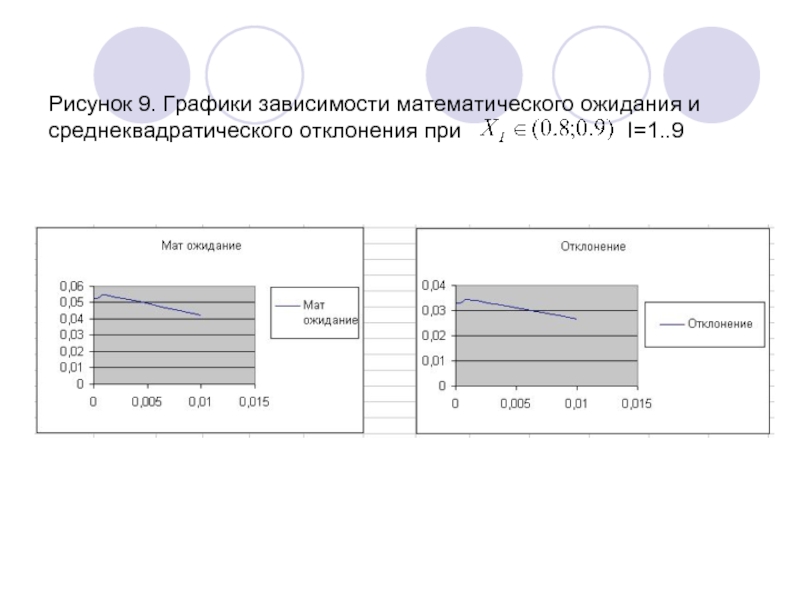
- 16. Рисунок 9. Графики зависимости математического ожидания и
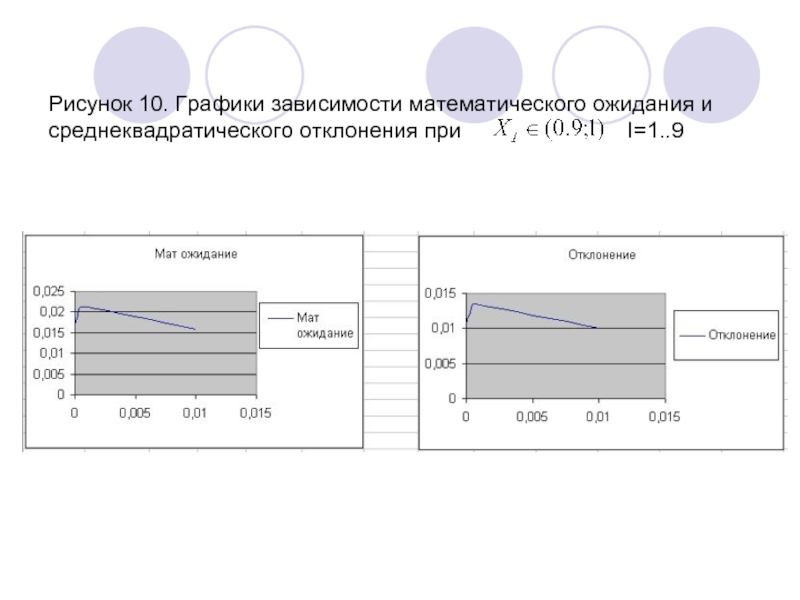
- 17. Рисунок 10. Графики зависимости математического ожидания и
- 18. Выводы Исследование системы на устойчивость показало, что
Слайд 1Устойчивость систем нелинейных дифференциальных уравнений
Выполнил студент ГИП-104
Шинкарёв Г.Г.
Научный руководитель:
Ибрагимов Т. М.
Слайд 2Цель работы
Целью данной курсовой работы является изучение устойчивости непрерывных
Слайд 3Постановка задачи
На основе изученного алгоритма проверить на устойчивость систему
Слайд 4Введение
Анализ устойчивости непосредственно связан с определением
Если достаточно малое возмущение приводит к существенному отклонению режима от исходного состояния или от невозмущенного движения, то говорят о нестабильности или неустойчивости положения равновесия или невозмущенного движения. Если же после прекращения действия возмущения система не отклоняется существенно от своего исходного состояния, то такой режим называют устойчивым.
Слайд 5Целочисленный пример
Рассматриваемая система дифференциальных уравнений является системой уравнений для оценки научной
uskor=3
I=125
U=12
Слайд 6
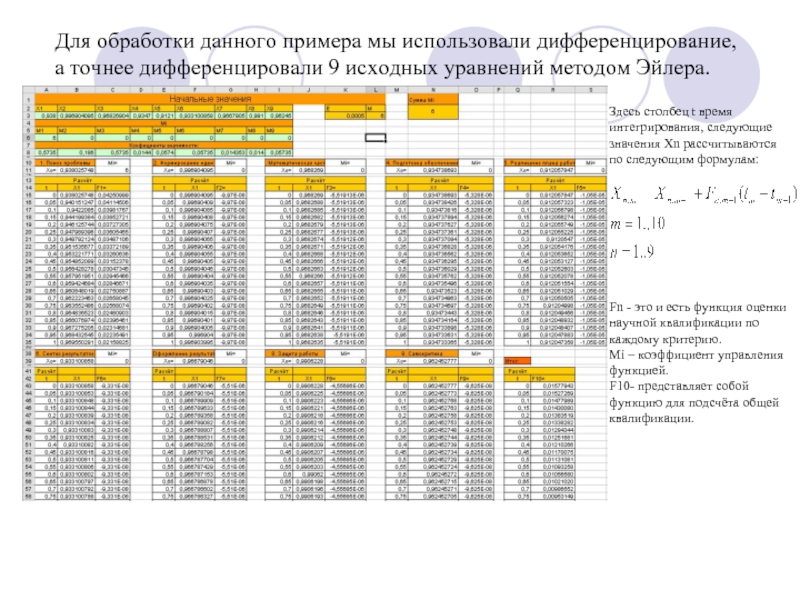
Для обработки данного примера мы использовали дифференцирование, а точнее дифференцировали 9
Дифференцирование
Здесь столбец t время интегрирования, следующие значения Хn рассчитываются по следующим формулам:
Fn - это и есть функция оценки научной квалификации по каждому критерию.
Mi – коэффициент управления функцией.
F10- представляет собой функцию для подсчёта общей квалификации.
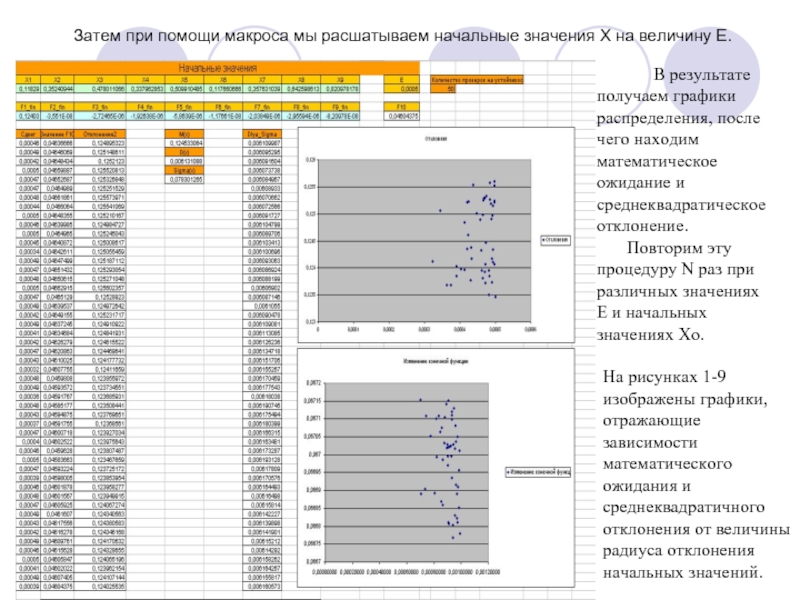
Слайд 7Затем при помощи макроса мы расшатываем начальные значения Х на величину
В результате получаем графики распределения, после чего находим математическое ожидание и среднеквадратическое отклонение.
Повторим эту процедуру N раз при различных значениях Е и начальных значениях Хо.
На рисунках 1-9 изображены графики, отражающие зависимости математического ожидания и среднеквадратичного отклонения от величины радиуса отклонения начальных значений.
Слайд 8Рисунок 1. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 9Рисунок 2. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 10Рисунок 3. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 11Рисунок 4. Графики зависимости математического ожидания и среднеквадратического отклонения при
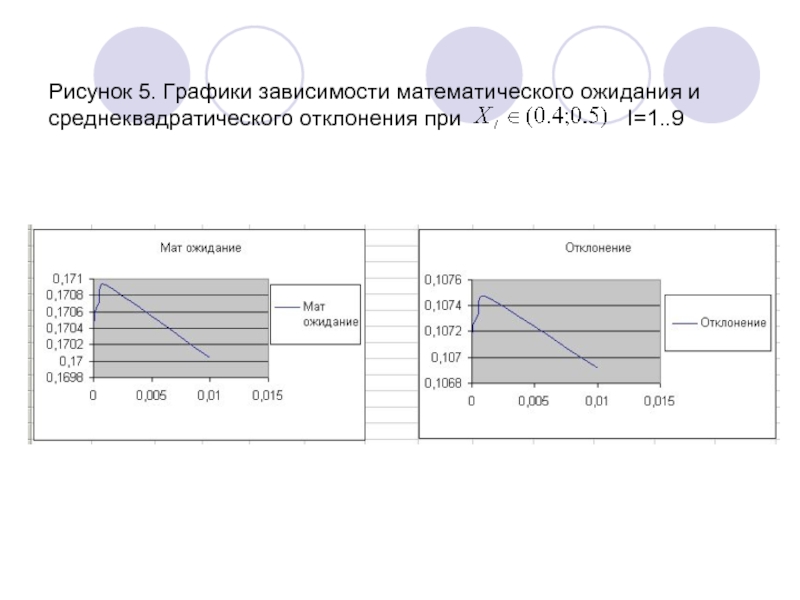
Слайд 12Рисунок 5. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 13Рисунок 6. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 14Рисунок 7. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 15Рисунок 8. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 16Рисунок 9. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 17Рисунок 10. Графики зависимости математического ожидания и среднеквадратического отклонения при
Слайд 18Выводы
Исследование системы на устойчивость показало, что при увеличении квалификации студентов устойчивость
Предположительно изменение устойчивости по грубой оценке соответствует экспоненциальному закону.
Есть и ряд факторов, которые могут, опять же предположительно, воздействовать негативно на устойчивость. Например это использование метода Эйлера. Продолжив работу в следующем семестре, я постараюсь проинтегрировать систему методом Рунге-Кутта. И оценить устойчивость системы. Я полагаю, что картина измениться. Тогда уже можно будет говорить о конкретных выводах