- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УСЛОВНО ИЗРАВНЕНИЕ НА ПЛАНОВИ/ДВУМЕРНИ МРЕЖИ. ОСНОВНИ ФИГУРИ презентация
Содержание
- 1. УСЛОВНО ИЗРАВНЕНИЕ НА ПЛАНОВИ/ДВУМЕРНИ МРЕЖИ. ОСНОВНИ ФИГУРИ
- 2. ОСНОВНИ ФИГУРИ Триъгълник Централна фигура Геодезически четириъгълник Венечна система
- 3. 1. УСЛОВНО ИЗРАВНЕНИЕ НА ОТДЕЛЕН ТРИЪГЪЛНИК
- 4. a b c β1 β2 β3
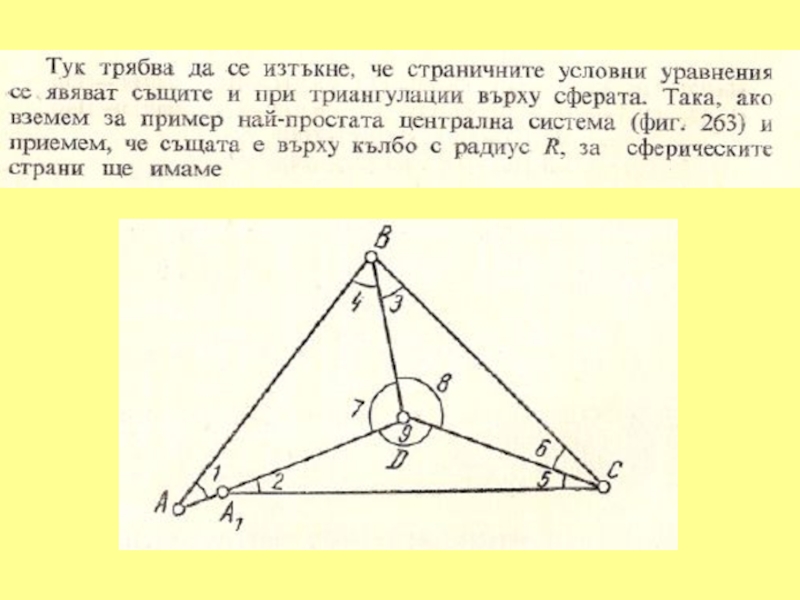
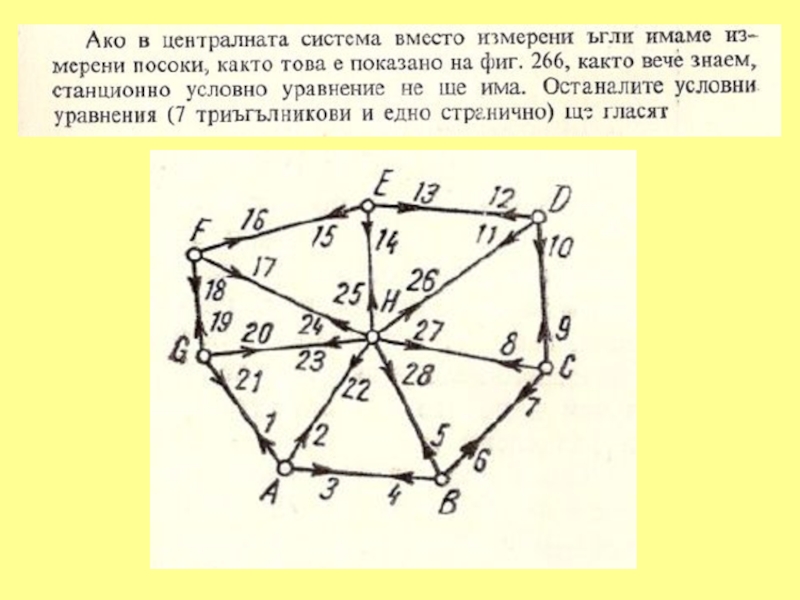
- 7. 1. УСЛОВНО ИЗРАВНЕНИЕ НА ЦЕНТРАЛНА СИСТЕМА
- 15. Развитието на една функция в Тейлоров ред
- 17. Означаваме : ctg (i) / ρcc
- 21. Общ вид на нормалните уравнения на корелатите
- 22. [aa/p]K1 + [ab/p]K2 + [ac/p]K3 +
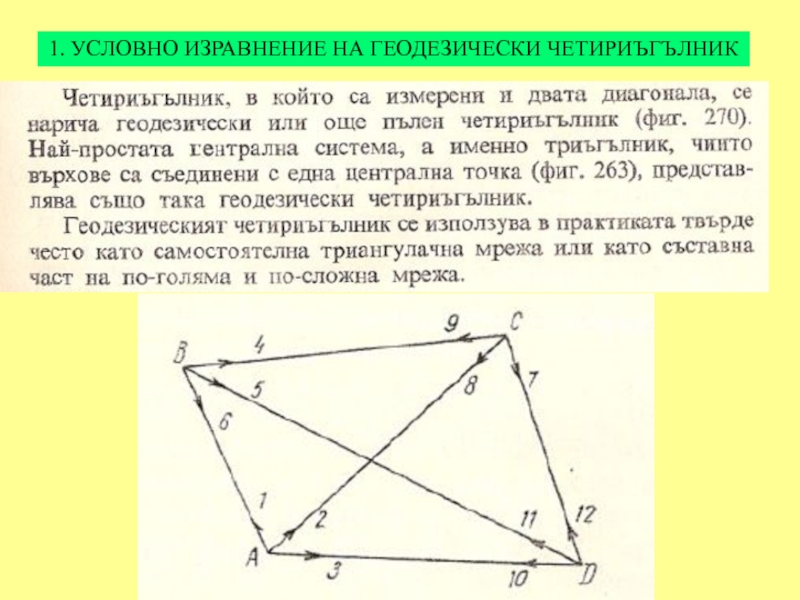
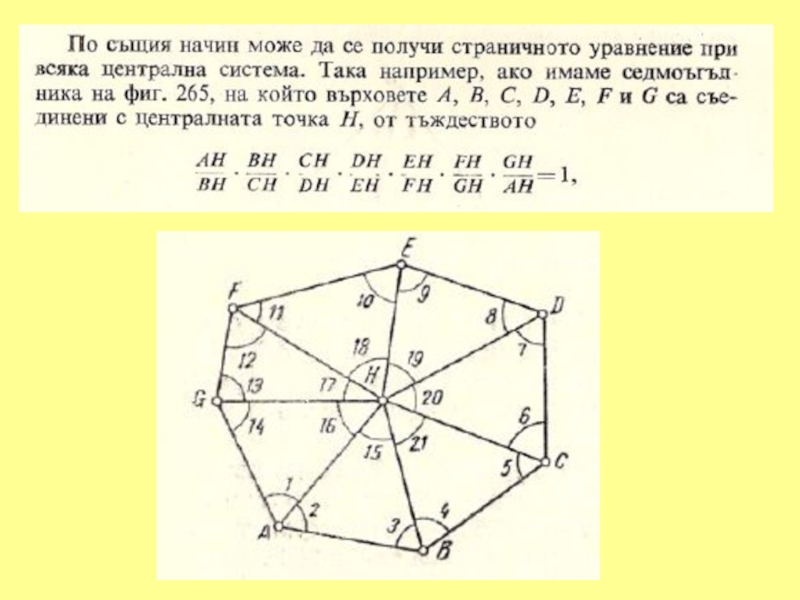
- 25. 1. УСЛОВНО ИЗРАВНЕНИЕ НА ГЕОДЕЗИЧЕСКИ ЧЕТИРИЪГЪЛНИК
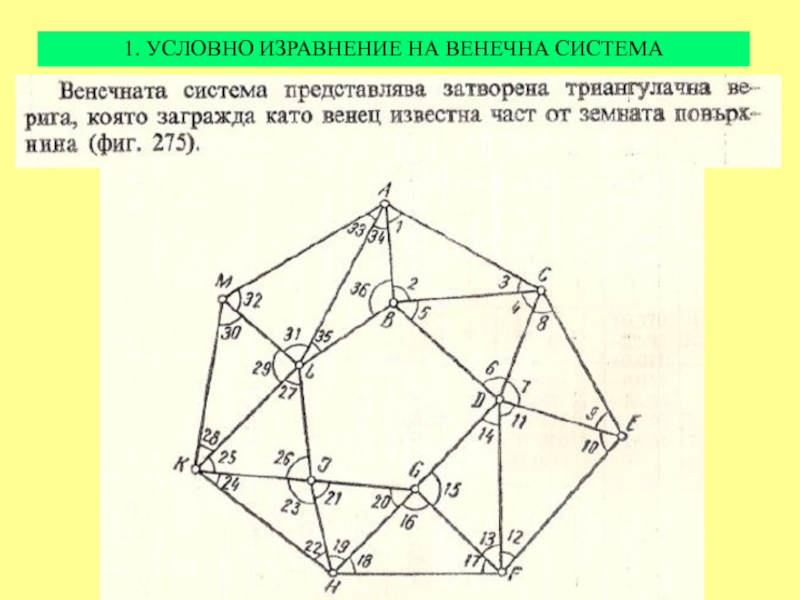
- 33. 1. УСЛОВНО ИЗРАВНЕНИЕ НА ВЕНЕЧНА СИСТЕМА
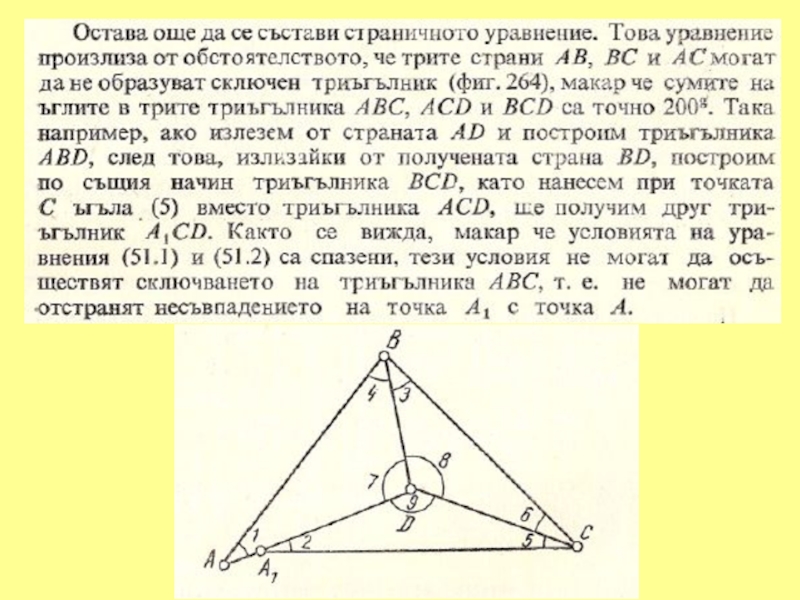
- 43. 1. УСЛОВНО ИЗРАВНЕНИЕ СВОБОДНИ ЪГЛОВИ МРЕЖИ С ПОВЕЧЕ ОТ ЕДНА БАЗА
Слайд 15Развитието на една функция в Тейлоров ред в общ вид е
F(X) = f{(x1+h1), {(x2+h2), . . ., {(xn+hn)} = f (x1, x2, . . . , xn) +
+ ∂f/∂x1.h1 + ∂f/∂x2.h2 + …+ ∂f/∂xn.hn + …
+ ∂f/∂x1.h1 + ∂f/∂x2.h2 + …+ ∂f/∂xn.hn + …
Слайд 16
sin {(1) + v1}. sin {(3) + v3}. sin {(5) + v5}
F(X) = ─────────────────────────── - 1 = 0
sin {(2) + v2}. sin {(4) + v4}. sin {(6) + v6}
cos (1). sin (1). sin (3). sin (5) cos (2). sin (1). sin (3). sin (5)
F(X) = F (0) + ───────────────── v1- ────────────────── v2 +
sin (1). sin (2) . sin (4). sin (6) sin2 (2). sin (4). sin (6)
cos (3). sin (3). sin (1). sin (5) cos (4). sin (1). sin (3). sin (5)
+ ───────────────── v3 - ────────────────── v4 + . . . = 0
sin (3). sin (2) . sin (4). sin (6) sin2 (4). sin (4). sin (6)
Където
sin (1). sin (3). sin (5)
F (0) = ─────────────
sin (2) . sin (4). sin (6)
F(X) = ─────────────────────────── - 1 = 0
sin {(2) + v2}. sin {(4) + v4}. sin {(6) + v6}
cos (1). sin (1). sin (3). sin (5) cos (2). sin (1). sin (3). sin (5)
F(X) = F (0) + ───────────────── v1- ────────────────── v2 +
sin (1). sin (2) . sin (4). sin (6) sin2 (2). sin (4). sin (6)
cos (3). sin (3). sin (1). sin (5) cos (4). sin (1). sin (3). sin (5)
+ ───────────────── v3 - ────────────────── v4 + . . . = 0
sin (3). sin (2) . sin (4). sin (6) sin2 (4). sin (4). sin (6)
Където
sin (1). sin (3). sin (5)
F (0) = ─────────────
sin (2) . sin (4). sin (6)
Слайд 17Означаваме : ctg (i) / ρcc = αi , където
ρcc = 636620
Тогава за страничното уравнение в окончателен линеен вид се получава
α1 v1 - α2v2 + α3v3 - α4v4 + α5v5 - α6v6 + w = 0
Така условните уравнения за по-голямата централна система ще бъдат
Тогава за страничното уравнение в окончателен линеен вид се получава
α1 v1 - α2v2 + α3v3 - α4v4 + α5v5 - α6v6 + w = 0
Така условните уравнения за по-голямата централна система ще бъдат
Слайд 21Общ вид на нормалните уравнения на корелатите :
[aa]K1 + [ab]K2 +
[ac]K3 + . . . . . . . . . + [ar]Kr + w1 = 0
[ab]K1 + [bb]K2 + [bc]K3 + . . . . . . . . . + [br]Kr + w2 = 0
[ac]K1 + [bc]K2 + [cc]K3 + . . . . . . . . . + [cr]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar]K1 + [br]K2 + [cr]K3 + . . . . . . . . . . + [rr]Kr +wr = 0
vi = ai K1 + bi K2 + ci K3+ . . . . . + ri Kr
me = ± √[vv] / r
[ab]K1 + [bb]K2 + [bc]K3 + . . . . . . . . . + [br]Kr + w2 = 0
[ac]K1 + [bc]K2 + [cc]K3 + . . . . . . . . . + [cr]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar]K1 + [br]K2 + [cr]K3 + . . . . . . . . . . + [rr]Kr +wr = 0
vi = ai K1 + bi K2 + ci K3+ . . . . . + ri Kr
me = ± √[vv] / r
Слайд 22
[aa/p]K1 + [ab/p]K2 + [ac/p]K3 + . . . . .
. . . . + [ar/p]Kr + w1 = 0
[ab/p]K1 + [bb/p]K2 + [bb/p]K3 + . . . . . . . . . + [br/p]Kr + w2 = 0
[ac/p]K1 + [bc/p]K2 + [cc/p]K3 + . . . . . . . . . + [cr/p]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar/p]K1 + [br/p]K2 + [cr/p]K3 + . . . . . . . . . . + [rr/p]Kr + wr = 0
vi = ai/pi K1 + bi/pi K2 + ci/pi K3+ . . . . . + ri/pi Kr
me = ± √[pvv] / r
[ab/p]K1 + [bb/p]K2 + [bb/p]K3 + . . . . . . . . . + [br/p]Kr + w2 = 0
[ac/p]K1 + [bc/p]K2 + [cc/p]K3 + . . . . . . . . . + [cr/p]Kr + w3 = 0
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
[ar/p]K1 + [br/p]K2 + [cr/p]K3 + . . . . . . . . . . + [rr/p]Kr + wr = 0
vi = ai/pi K1 + bi/pi K2 + ci/pi K3+ . . . . . + ri/pi Kr
me = ± √[pvv] / r













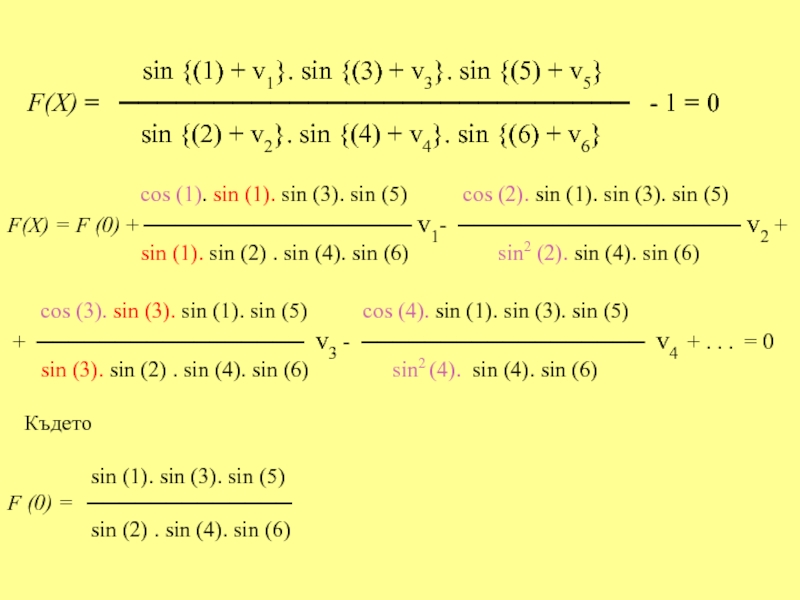



![Общ вид на нормалните уравнения на корелатите :[aa]K1 + [ab]K2 + [ac]K3 + . .](/img/tmb/3/219049/045d438756264ac7beee7bc132e1e8d2-800x.jpg)
![[aa/p]K1 + [ab/p]K2 + [ac/p]K3 + . . . . . . . . .](/img/tmb/3/219049/a9b91535db42f39c429040f9005bc33d-800x.jpg)