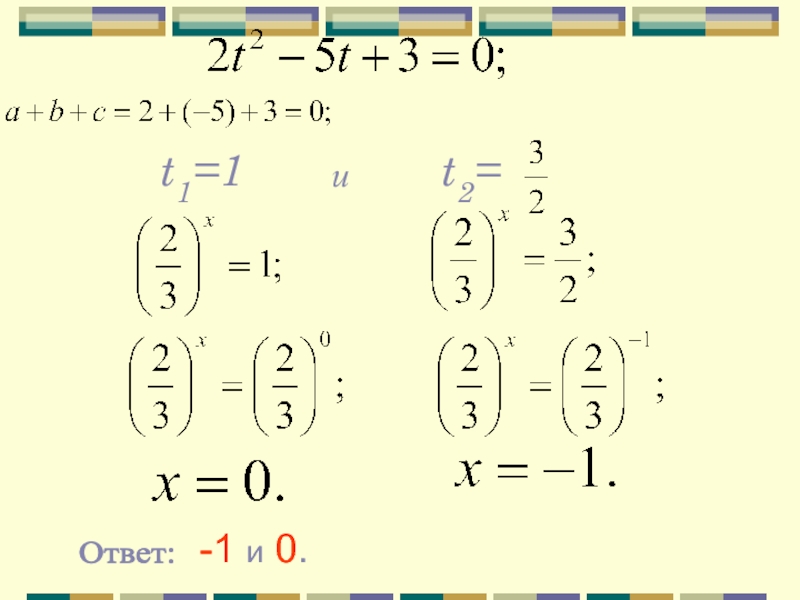«Показательные уравнения
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок по теме Показательные уравнения презентация
Содержание
- 2. 1).Представить выражение в виде степени с рациональным показателем:
- 3. 2).Вычислить: 3).Найти область определения выражения:
- 4. 4).Разложить на множители: Выносим степень с меньшим показателем!
- 5. 4).Какие из перечисленных функций показательные:
- 6. 5).Какие из перечисленных функций возрастают, какие убывают:
- 7. 6).Дана функция у=6 и
- 8. Все уравнения можно рассматривать, как равенства двух
- 9. Тема: «Решение показательных
- 10. I.Простейшие показательные уравнения вида а). D(у)=R;
- 12. 2).В уравнении
- 13. II. Показательные уравнения вида а).
- 14. Пример 1:
- 15. III. Показательные уравнения вида
- 16. Возможны три случая:
- 17. Пример 1:
- 18. IV. Трёхчленное показательное уравнение:
- 19. Пример:
- 20. б). Разделим данное
- 21. Пример:
- 23. Ответить на вопросы: Какие уравнения называются показательными?
- 24. Устно: решить показательные уравнения (по выбору):
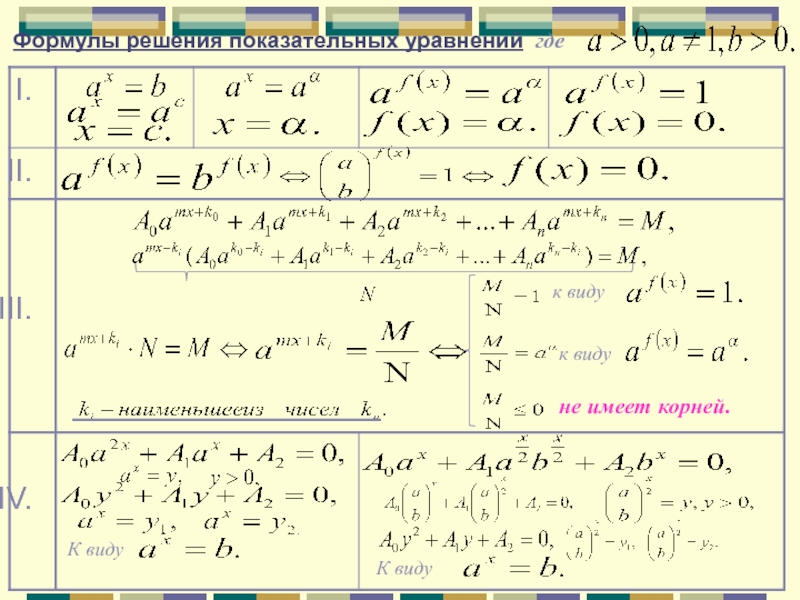
- 25. к виду к виду не
- 26. Индивидуальная работа. Из данных вариантов решить один(по
- 27. Итоги урока. Какие уравнения называются показательными?
1).Представить выражение в виде степени с рациональным показателем:
Слайд 76).Дана функция у=6 и значения у,
равные 1,5; 12; 6; .
Выбрать те значения у, при которых х<0.
7).Решить уравнения:
К какому виду уравнений относится каждое из данных?
Слайд 8Все уравнения можно рассматривать, как равенства двух функций f(x) =φ(x).
Задача решения
уравнений заключается в отыскании всех тех значений х, для каждого из которых значения функций f(x) и φ(x) равны между собой.
Областью определения уравнения называется общая часть областей определения каждой из функций.
Обычно вид уравнения определяется функцией, содержащейся в этом уравнении:
линейное, квадратичное, тригонометрическое и
показательное.
Областью определения уравнения называется общая часть областей определения каждой из функций.
Обычно вид уравнения определяется функцией, содержащейся в этом уравнении:
линейное, квадратичное, тригонометрическое и
показательное.
Слайд 9Тема: «Решение показательных
уравнений».
Задачи урока:
Познакомиться с видами показательных уравнений.
Рассмотреть способы решений показательных уравнений различных видов.
Отработать навыки и умения решения показательных уравнений.
Слайд 10I.Простейшие показательные уравнения вида
а).
D(у)=R;
Е(у)=
Монотонна на всей области определения,
при a >1
возрастает,при 0< a <1 убывает, т.е
по теореме о корне уравнение
Имеет один корень при b>0;
Не имеет корней при b 0.
Представим b в виде имеем:
по теореме о корне уравнение
Имеет один корень при b>0;
Не имеет корней при b 0.
Представим b в виде имеем:
Слайд 11
по свойству
степеней с одинаковыми основаниями
решением уравнения является равенство х = с.
Пример:
Ответ: 4.
степеней с одинаковыми основаниями
решением уравнения является равенство х = с.
Пример:
Ответ: 4.
Слайд 122).В уравнении
, левая и правая части приведены к одному основанию и решением уравнения является равенство х =
Т.к. разделим обе части уравнения на правую часть:
3).Очевидно, что уравнение
Пример:
Т.к. разделим обе части уравнения на правую часть:
3).Очевидно, что уравнение
Пример:
Ответ:
Слайд 13II. Показательные уравнения вида
а).
На основании определения о нулевом показателе имеем его решение:
Пример:
Ответ: 2 и 3.
б).
Уравнения такого вида решаются с использованием теорем о возведении в степень произведения и дроби и им обратные, рассмотрим решение на примере:
Слайд 15III. Показательные уравнения вида
где
Вынесем за скобки где -наименьшее число. Имеем:
при N≠0 получим уравнение:
Слайд 16 Возможны три случая:
, уравнение сводится к виду
, уравнение сводится к виду
, данное уравнение не имеет корней.
, уравнение сводится к виду
, данное уравнение не имеет корней.
Слайд 17 Пример 1:
Вынесем за скобки
Пример 2:
Вынесем за скобки
уравнение корней не имеет.
корней нет.
Ответ:
Ответ:
Слайд 18IV. Трёхчленное показательное уравнение:
а).
Выполним подстановку где у>0,
показательное уравнение превращается в обычное квадратное уравнение
Решением этого уравнения являются значения
Чтобы найти корни показательного уравнения нужно решить уравнения и
Если и одновременно, то данное показательное уравнение корней не имеет.
Выполним подстановку где у>0,
показательное уравнение превращается в обычное квадратное уравнение
Решением этого уравнения являются значения
Чтобы найти корни показательного уравнения нужно решить уравнения и
Если и одновременно, то данное показательное уравнение корней не имеет.
Слайд 20б).
Разделим данное уравнение на bx, ( bx≠0):
Решение
этого уравнения сводится к решению квадратного уравнения:
Чтобы найти корни показательного уравнения нужно
решить уравнения и
Чтобы найти корни показательного уравнения нужно
решить уравнения и
y>0
где
Слайд 21 Пример:
Преобразуем уравнение по свойствам степени:
Разделим уравнение на 32х, 32х≠0:
выполним подстановку
Решим уравнение
Слайд 23Ответить на вопросы:
Какие уравнения называются показательными?
Сколько корней имеет уравнение вида:
Когда показательное
уравнение не имеет корней?
Слайд 26Индивидуальная работа.
Из данных вариантов решить один(по выбору):
Дополнительно:
Дополнительно:
III уровень
+1б.
+1б.
+1б.
+1б.
+1б.
а).24х=16; б).3х=1.
а).33х=27;
б).4х=-64.
+1б.
II уровень
I уровень
Слайд 27Итоги урока.
Какие уравнения называются показательными?
К какому типу уравнений относятся показательные
уравнения? Почему?
Какие виды показательных уравнений рассмотрели?
Сколько решений может иметь показательное уравнение? Когда оно не имеет корней?
Домашнее задание:
Какие виды показательных уравнений рассмотрели?
Сколько решений может иметь показательное уравнение? Когда оно не имеет корней?
Домашнее задание:
