- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Урок конференцияО теореме Пифагора и способах её доказательств презентация
Содержание
- 1. Урок конференцияО теореме Пифагора и способах её доказательств
- 2. Цели: 1) Доказать теорему Пифагора несколькими способами;
- 3. Историческая справка За тысячелетие за Пифагора
- 4. «Пифагоровы штаны во все стороны равны» Площадь
- 5. Теорема Пифагора и способы ее доказательства
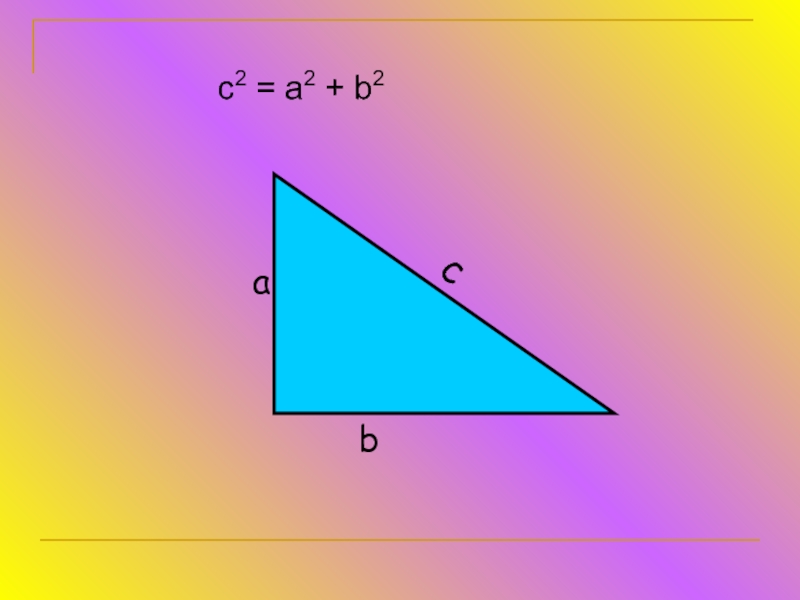
- 6. Теорема Пифагора В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин его катетов.
- 8. Аддитивный метод Этот вид доказательства основан на
- 10. Индийский Способ Доказательства
- 11. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
- 12. Рассмотрим прямоугольный треугольник с катетами
- 13. Достроим треугольник до квадрата со стороной
- 14. Доказательство Бхаскары
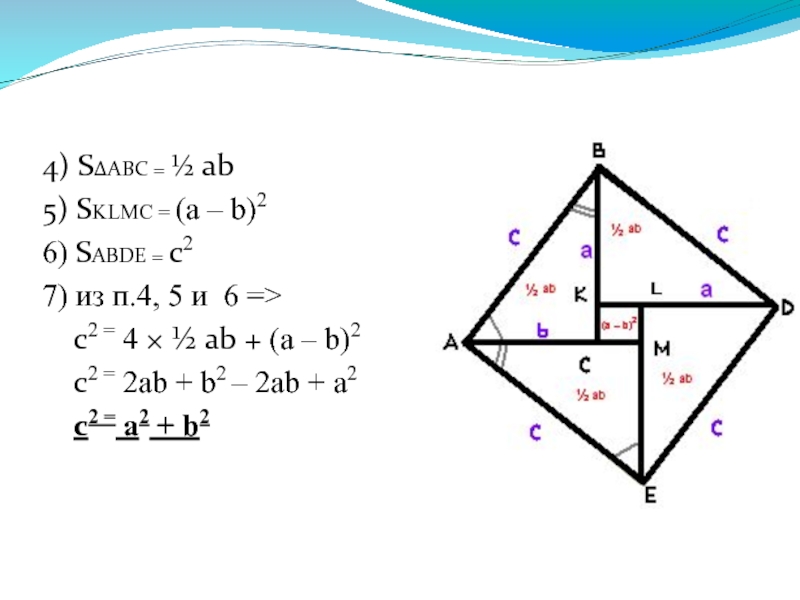
- 15. Дано: ABDE – квадрат
- 16. Доказательство: 1) ΔABC = ΔBDK = ΔDEL
- 17. 4) SΔABC = ½ ab 5)
- 18. Доказательство Гарфилда
- 19. Пусть BA=b; AС=а; BС=с Строим прямоугольный
- 20. BAED-прямоугольная трапеция BA AE; DE
- 21. ΔBCD-прямоугольный т.к
- 22. SBAED= SBAC +SCED+SBCD SBAED=½·ba+½·ba+½·c² С
- 23. Доказательство Эвклида
- 24. Пусть АВС – прямоугольный треугольник,
- 25. Проведем отрезок АМ (перпендикулярный ВС).
- 26. Проведем вспомогательные прямые DC и
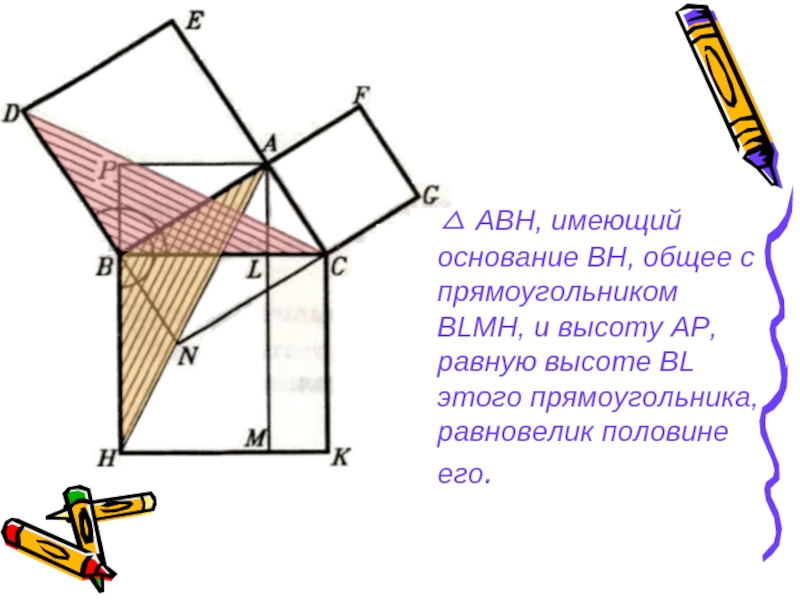
- 27. △ АВН, имеющий основание ВН,
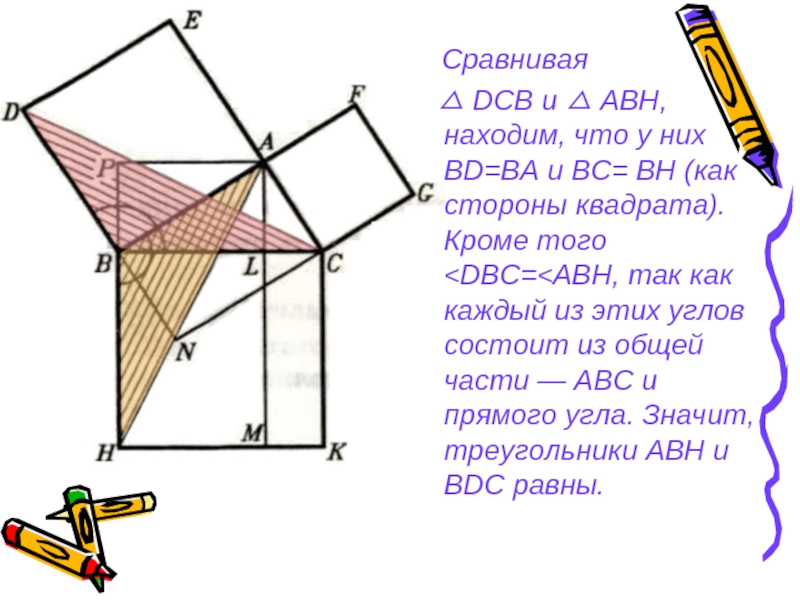
- 28. Сравнивая △
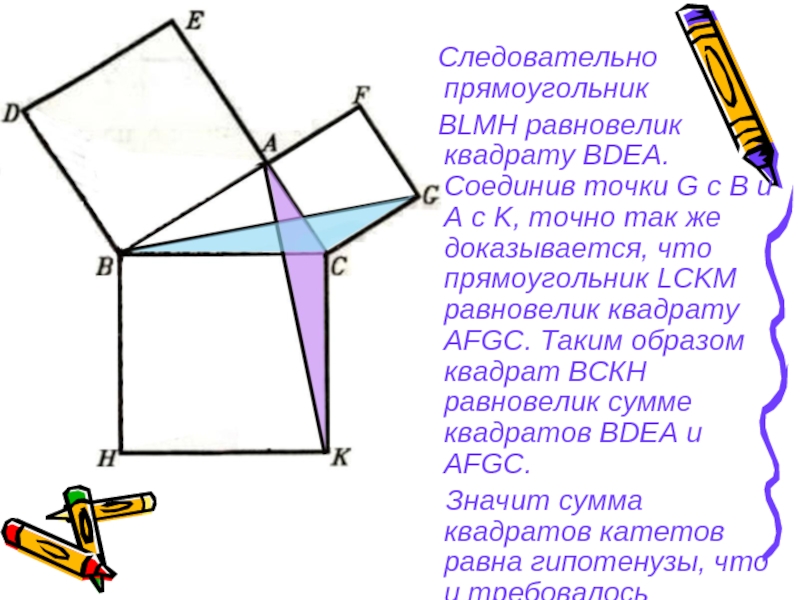
- 29. Следовательно прямоугольник
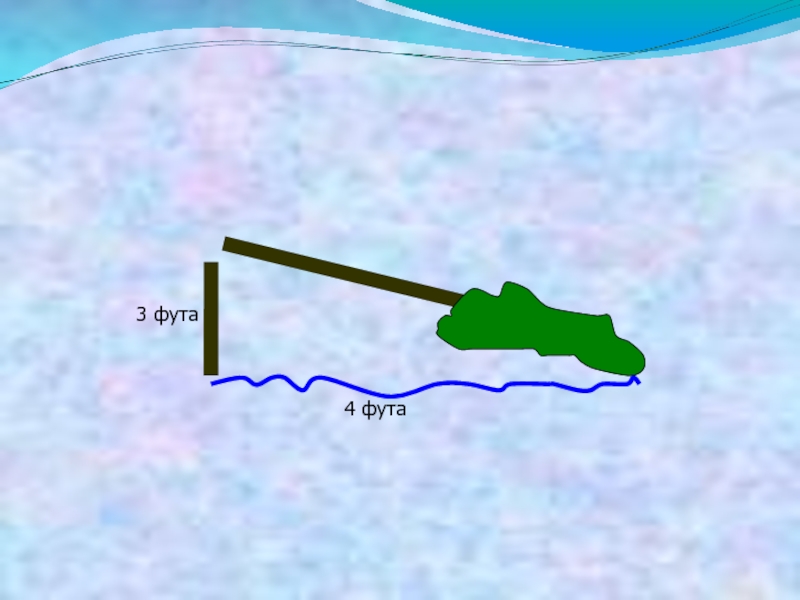
- 30. Индийская задача о тополе На
- 31. 4 фута 3 фута
- 32. 4 фута 3 фута 1 фут=30,5 см.
- 33. Решение индийской задачи о тополе Из
- 34. Задача о лотосе Над озером тихим
- 35. А В С
- 36. Решение задачи о лотосе Цветок лотоса возвышался
- 37. Задача птица у реки
- 38. В С А х 50-х 20 30
- 39. Решение задачи птица у реки Из схематического
- 40. Проект разработали учащиеся 8 «Б» класса.
Слайд 2Цели:
1) Доказать теорему Пифагора несколькими способами; добиться понимания поставленной задачи, учить
объяснять выполненное решение;
2) Создать условие для развития умения выстраивания логические цепочки, учить думать, высказывать своё мнение;
3) Познакомить с жизнедеятельностью Пифагора, воспитывать гордость за полученные знания, прививать интерес к исследованиям, истории математики.
2) Создать условие для развития умения выстраивания логические цепочки, учить думать, высказывать своё мнение;
3) Познакомить с жизнедеятельностью Пифагора, воспитывать гордость за полученные знания, прививать интерес к исследованиям, истории математики.
Слайд 3Историческая справка
За тысячелетие за Пифагора (VI в. до н. э.) было
известно утверждение: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Заслуга Пифагора является открытие доказательства этой теоремы.
Доказательство самого Пифагора до нас не дошло. В настоящее время имеется свыше 150 различных доказательств этой теоремы.
За восемь веков до нашей эры теорема Пифагора была хорошо известна индийцам под названием «Правило верёвки» и использовалось ими для построения алтарей, которые, согласно Священному писанью, должны иметь строгую геометрическую форму, ориентированную относительно четырёх сторон горизонта. Верёвочный треугольник со сторонами равными 3, 4 , 5 («египетский треугольник»), образовывался веревками, натянутыми на колышки, воткнутые в землю в вершинах треугольника. Отсюда и название древних землемеров. В практике при построении прямого угла треугольник со сторонами 3, 4 , 5 известен был уже в глубокой древности египтянам и другим народам
Востока, такие пропорции археологи
находят и в размерах тесаных плит
пирамиды Хефрена, и в царской комнате
пирамиды Хеопса.
Раньше теорема Пифагора
называлась «магистром математики»,
потому что вместо экзамена математике
студент должен был принести присягу,
что читал установленное число глав
«Начал» Евклида. Фактически никто не
прочитывал больше первой книги (главы)
«Начал». Поэтому последняя теорема
первой книги (теорема Пифагора) носила название «магистра математики».
Доказательство самого Пифагора до нас не дошло. В настоящее время имеется свыше 150 различных доказательств этой теоремы.
За восемь веков до нашей эры теорема Пифагора была хорошо известна индийцам под названием «Правило верёвки» и использовалось ими для построения алтарей, которые, согласно Священному писанью, должны иметь строгую геометрическую форму, ориентированную относительно четырёх сторон горизонта. Верёвочный треугольник со сторонами равными 3, 4 , 5 («египетский треугольник»), образовывался веревками, натянутыми на колышки, воткнутые в землю в вершинах треугольника. Отсюда и название древних землемеров. В практике при построении прямого угла треугольник со сторонами 3, 4 , 5 известен был уже в глубокой древности египтянам и другим народам
Востока, такие пропорции археологи
находят и в размерах тесаных плит
пирамиды Хефрена, и в царской комнате
пирамиды Хеопса.
Раньше теорема Пифагора
называлась «магистром математики»,
потому что вместо экзамена математике
студент должен был принести присягу,
что читал установленное число глав
«Начал» Евклида. Фактически никто не
прочитывал больше первой книги (главы)
«Начал». Поэтому последняя теорема
первой книги (теорема Пифагора) носила название «магистра математики».
Слайд 4«Пифагоровы штаны во все стороны равны»
Площадь квадрата,
построенного на гипотенузе
прямоугольного
треугольника, равна
сумме
площадей квадратов,
построенных на его катетах.
построенных на его катетах.
Слайд 6Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин
его катетов.
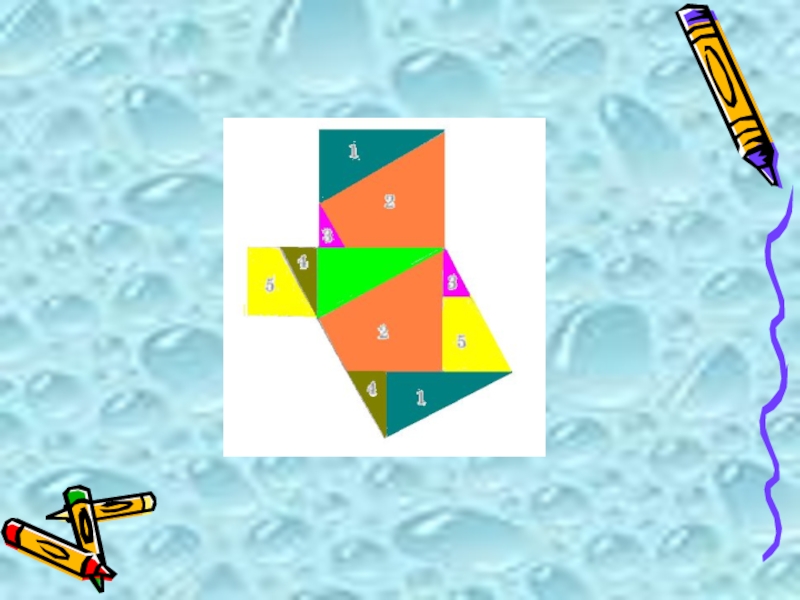
Слайд 8Аддитивный метод
Этот вид доказательства основан на разложении квадратов, построенных на катетах,
на фигуры, из которых можно сложить квадрат, построенный на гипотенузе.
Слайд 12 Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой
c. Докажем, что с2 = a2+ b2
Слайд 13Достроим треугольник
до квадрата со стороной a + b
так, как показано
на рисунке.
Площадь этого квадрата равна
(a + b)2 . С другой стороны,
этот квадрат составлен из
четырёх равных прямоугольных
треугольников , площадь каждого
из которых равна 1/2 аb , и квадрата со стороной с,
поэтому:
S=4 · 1/2 а b +с2=2аb+с2 .
Таким образом ,
(a + b)² = 2аb+с² , a²+2ab+b² =2ab+c²,
откуда с2 =а2 +b2 .
Площадь этого квадрата равна
(a + b)2 . С другой стороны,
этот квадрат составлен из
четырёх равных прямоугольных
треугольников , площадь каждого
из которых равна 1/2 аb , и квадрата со стороной с,
поэтому:
S=4 · 1/2 а b +с2=2аb+с2 .
Таким образом ,
(a + b)² = 2аb+с² , a²+2ab+b² =2ab+c²,
откуда с2 =а2 +b2 .
Слайд 15
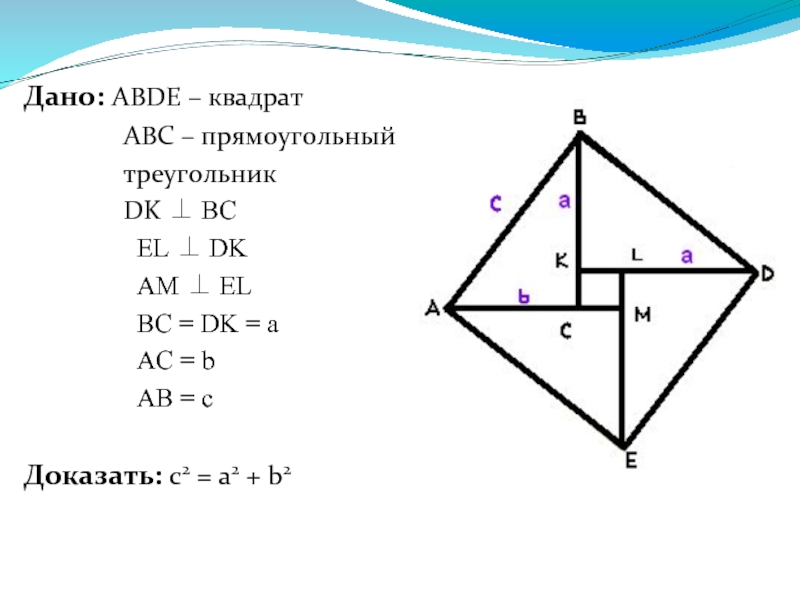
Дано: ABDE – квадрат
ABC – прямоугольный
треугольник
DK ⊥ BC
EL ⊥ DK
AM ⊥ EL
BC = DK = a
AC = b
AB = c
Доказать: c2 = a2 + b2
треугольник
DK ⊥ BC
EL ⊥ DK
AM ⊥ EL
BC = DK = a
AC = b
AB = c
Доказать: c2 = a2 + b2
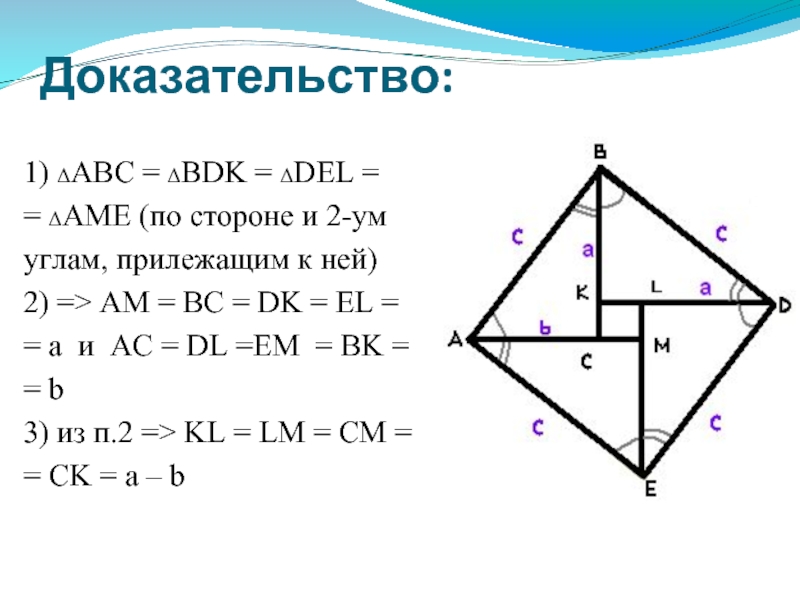
Слайд 16Доказательство:
1) ΔABC = ΔBDK = ΔDEL =
= ΔAME (по стороне и
2-ум
углам, прилежащим к ней)
2) => AM = BC = DK = EL =
= a и AC = DL =EM = BK =
= b
3) из п.2 => KL = LM = CM =
= CK = a – b
углам, прилежащим к ней)
2) => AM = BC = DK = EL =
= a и AC = DL =EM = BK =
= b
3) из п.2 => KL = LM = CM =
= CK = a – b
Слайд 17
4) SΔABC = ½ ab
5) SKLMC = (a – b)2
6)
SABDE = c2
7) из п.4, 5 и 6 =>
c2 = 4 × ½ ab + (a – b)2
c2 = 2ab + b2 – 2ab + a2
c2 = a2 + b2
7) из п.4, 5 и 6 =>
c2 = 4 × ½ ab + (a – b)2
c2 = 2ab + b2 – 2ab + a2
c2 = a2 + b2
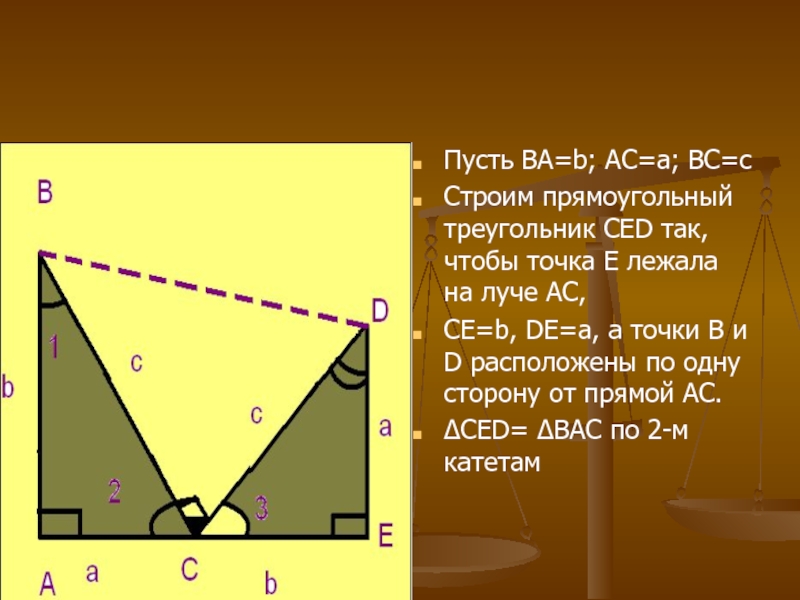
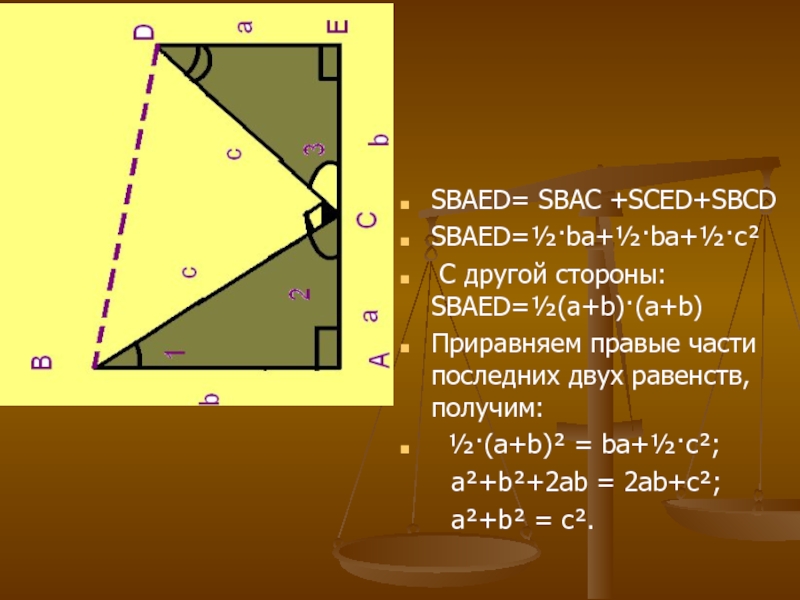
Слайд 19Пусть BA=b; AС=а; BС=с
Строим прямоугольный треугольник CED так, чтобы точка
Е лежала на луче АС,
СЕ=b, DE=a, а точки B и D расположены по одну сторону от прямой АС.
ΔCED= ΔBAC по 2-м катетам
СЕ=b, DE=a, а точки B и D расположены по одну сторону от прямой АС.
ΔCED= ΔBAC по 2-м катетам
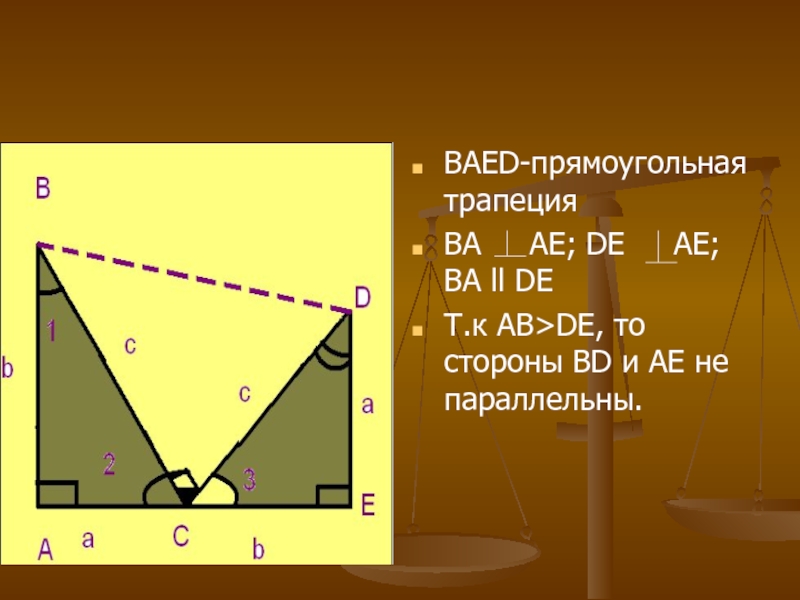
Слайд 20BAED-прямоугольная трапеция
BA AE; DE AE; BA ll
DE
Т.к АB>DE, то стороны BD и AE не параллельны.
Т.к АB>DE, то стороны BD и AE не параллельны.
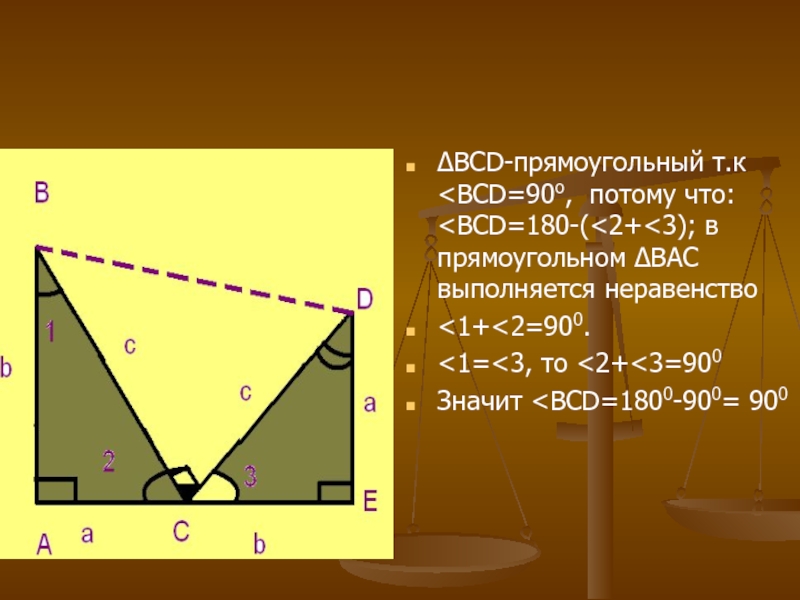
Слайд 22
SBAED= SBAC +SCED+SBCD
SBAED=½·ba+½·ba+½·c²
С другой стороны: SBAED=½(a+b)·(a+b)
Приравняем правые части последних двух
равенств, получим:
½·(a+b)² = ba+½·c²;
a²+b²+2ab = 2ab+c²;
a²+b² = c².
½·(a+b)² = ba+½·c²;
a²+b²+2ab = 2ab+c²;
a²+b² = c².
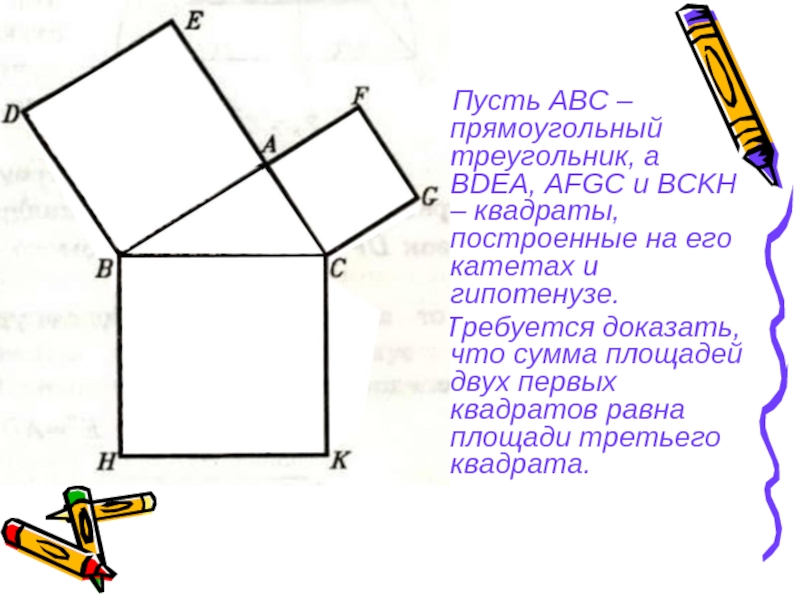
Слайд 24 Пусть АВС – прямоугольный треугольник, а BDEA, AFGC и
BCKH – квадраты, построенные на его катетах и гипотенузе.
Требуется доказать, что сумма площадей двух первых квадратов равна площади третьего квадрата.
Требуется доказать, что сумма площадей двух первых квадратов равна площади третьего квадрата.
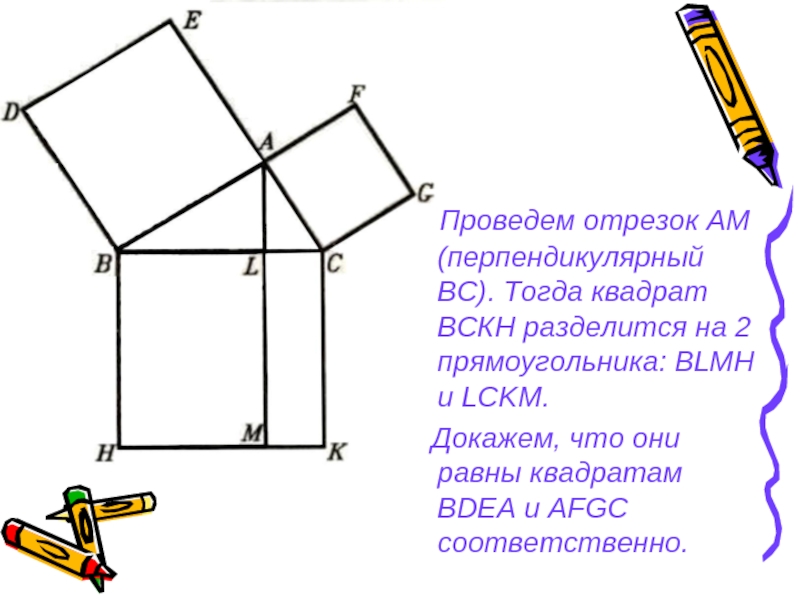
Слайд 25 Проведем отрезок АМ (перпендикулярный ВС). Тогда квадрат ВСКН разделится
на 2 прямоугольника: BLMH и LCKM.
Докажем, что они равны квадратам BDEA и AFGC соответственно.
Докажем, что они равны квадратам BDEA и AFGC соответственно.
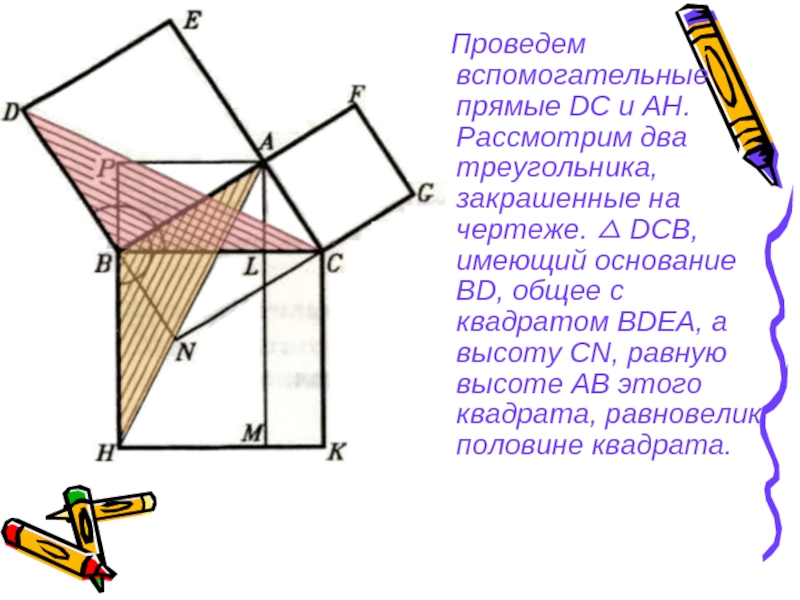
Слайд 26 Проведем вспомогательные прямые DC и AH. Рассмотрим два треугольника,
закрашенные на чертеже. △ DCB, имеющий основание BD, общее с квадратом BDЕА, а высоту CN, равную высоте АВ этого квадрата, равновелик половине квадрата.
Слайд 27 △ АВН, имеющий основание ВН, общее с прямоугольником BLMH,
и высоту AP, равную высоте BL этого прямоугольника, равновелик половине его.
Слайд 28 Сравнивая
△ DCB и △ АВН, находим,
что у них BD=ВА и BС= ВН (как стороны квадрата). Кроме того
Слайд 29 Следовательно прямоугольник
BLMH равновелик квадрату BDEA. Соединив
точки G с B и A с K, точно так же доказывается, что прямоугольник LCKM равновелик квадрату AFGC. Таким образом квадрат ВСКН равновелик сумме квадратов BDEA и AFGC.
Значит сумма квадратов катетов равна гипотенузы, что и требовалось доказать.
Значит сумма квадратов катетов равна гипотенузы, что и требовалось доказать.
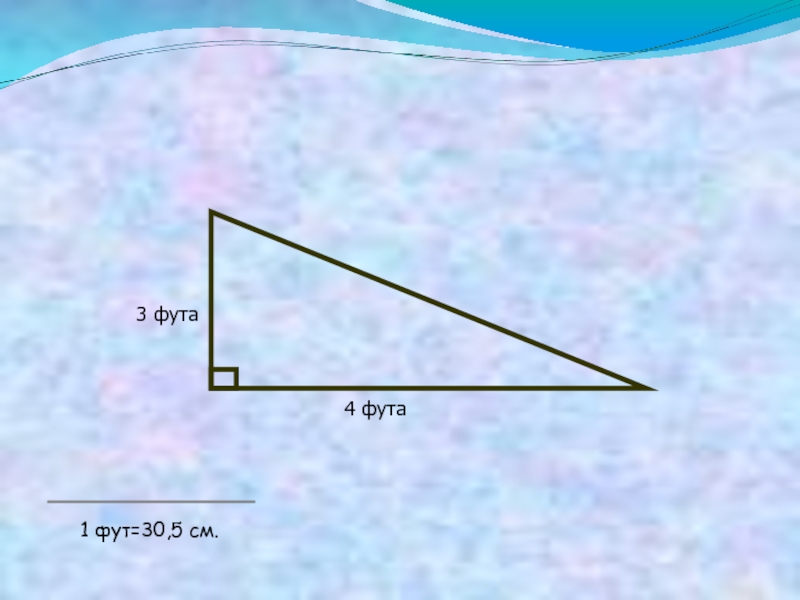
Слайд 30Индийская задача о тополе
На берегу рос тополь одинокий.
Вдруг ветра порыв
его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его составлял.
Запомни теперь, что в том месте река
Лишь в четыре фута была широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи,
У тополя как велика высота.
Бедный тополь упал. И угол прямой
С теченьем реки его составлял.
Запомни теперь, что в том месте река
Лишь в четыре фута была широка.
Верхушка склонилась у края реки,
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи,
У тополя как велика высота.
Слайд 33Решение индийской задачи о тополе
Из условия задачи следует, что
отломившееся часть
ствола является
гипотенузой прямоугольного
треугольника, катеты которого 3 и 4 фута
образованы высотой оставшейся части
ствола и шириной реки. Поэтому длинна
упавшей части ствола – 5 футов, а высота
всего дерева 8 футов.
гипотенузой прямоугольного
треугольника, катеты которого 3 и 4 фута
образованы высотой оставшейся части
ствола и шириной реки. Поэтому длинна
упавшей части ствола – 5 футов, а высота
всего дерева 8 футов.
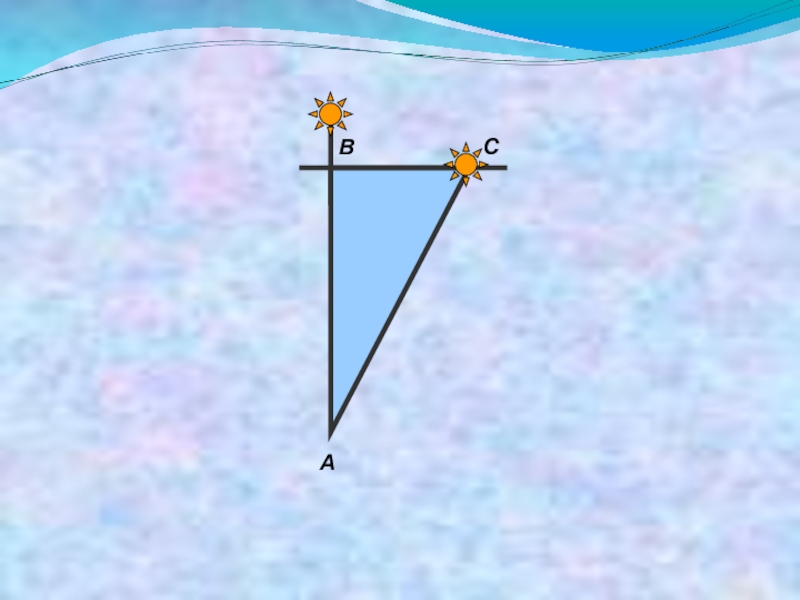
Слайд 34Задача о лотосе
Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос
одиноко,
И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак предложу я вопрос:
Как озеро вода здесь глубока?
И ветер порывом
Отнес его в сторону. Нет
Боле цветка над водой.
Нашел же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак предложу я вопрос:
Как озеро вода здесь глубока?
Слайд 36Решение задачи о лотосе
Цветок лотоса возвышался над уровнем озера на полфута.
Порыв ветра отклонил его стебель, и цветок оказался на уровне воды в двух футах от прежнего места. Задачу можно рассматривать как требование найти катет прямоугольного треугольника, длинна которого – подводный отрезок стебля, второй катет равен двум футам, а гипотенуза – отрезок, длинна которого равна всей длине стебля. Итак, глубину озера, равную длине подводной части стебля (отрезок АВ), обозначим через x, тогда гипотенуза АС будет х+1/2, отрезок ВС – 2 фута.
Составим уравнение:
Составим уравнение:
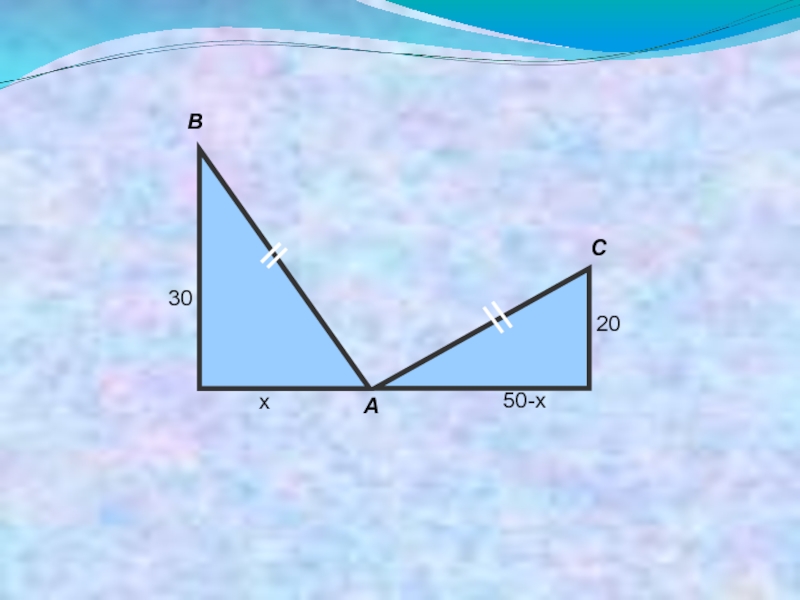
Слайд 37Задача птица у реки
На обоих берегах реки растет по пальме, одна
против другой. Высота одной – 30 локтей, другой – 20 локтей. На верхушке каждой пальмы сидит птица. Расстояние между основаниями пальм – 50 локтей. Внезапно обе птицы заметили рыбу, выплывающую на поверхность воды между пальмами. Они кинулись к ней разом и достигли её одновременно. На каком расстоянии от основания более высокой пальмы появилась рыба?
Слайд 39Решение задачи птица у реки
Из схематического чертежа, пользуясь теоремой Пифагора, устанавливаем:
АВ2=302+х2, АС2=202+(50-х)2. Но АВ=АС, так как обе птицы пролетели эти расстояния за одно и тоже время. Поэтому 302+х2=202+(50-х)2; х=20.
Ответ: рыба появилась в 20 локтях от той пальмы, высота которой 30 локтей.
Ответ: рыба появилась в 20 локтях от той пальмы, высота которой 30 локтей.
Слайд 40Проект разработали учащиеся
8 «Б» класса.
Руководитель проекта:
Давыдова Елена Александровна
2013