- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (II) презентация
Содержание
- 1. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ (II)
- 2. Одним из наиболее распространенных уравнений
- 3. Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения.
- 4. Двумерное волновое уравнение используется для исследования колебаний тонкой пластины (мембраны).
- 5. Трехмерное волновое уравнение описывает распространение волн
- 6. Рассмотрим одномерное волновое уравнение c начальными условиями
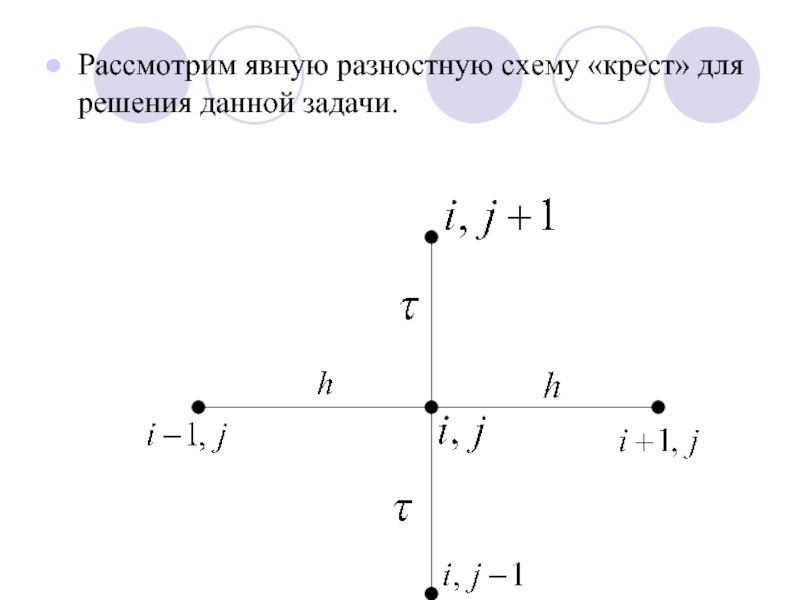
- 7. Рассмотрим явную разностную схему «крест» для решения данной задачи.
- 8. Заменим в уравнении вторые производные искомой
- 9. Отсюда можно найти явное выражение для
- 10. Здесь, для определения неизвестных значений на
- 11. решения на нулевом и первом слоях
- 12. Для получения решения на первом слое воспользуемся
- 13. Построим неявную схему. Вторую
- 15. Из этого соотношения можно получить систему уравнений
- 16. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ Интегральным уравнением называется уравнение,
- 17. Виды интегральных уравнений. Уравнения,
- 18. Одним из них является уравнение Фредгольма первого
- 19. уравнение Вольтерра первого рода: уравнение Вольтерра второго рода
- 20. Для решения линейных интегральных уравнений строится
Слайд 2
Одним из наиболее распространенных уравнений с частными производными второго порядка является
волновое уравнение, описывающее различные виды колебаний.
Слайд 3
Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные
колебательные движения.
Слайд 4
Двумерное волновое уравнение используется для исследования колебаний тонкой пластины (мембраны).
Слайд 5
Трехмерное волновое уравнение описывает распространение волн в пространстве (например, звуковых волн
в жидко- жидкости).
Слайд 8
Заменим в уравнении вторые производные искомой функции U по t и
х их конечно-разностными соотношениями.
Слайд 10
Здесь, для определения неизвестных значений на (j + 1)-м слое нужно
знать решения на j-м и (j — 1)-м слоях.
Поэтому начать счет можно лишь для второго слоя.
Поэтому начать счет можно лишь для второго слоя.
Слайд 11
решения на нулевом и первом слоях находятся с помощью начальных условий.
На
нулевом слое имеем
Слайд 12Для получения решения на первом слое воспользуемся вторым начальным условием.
Производную
заменим конечно-разностной аппроксимацией.
Из этого соотношения можно найти значения сеточной функции на первом слое:
Из этого соотношения можно найти значения сеточной функции на первом слое:
Слайд 13
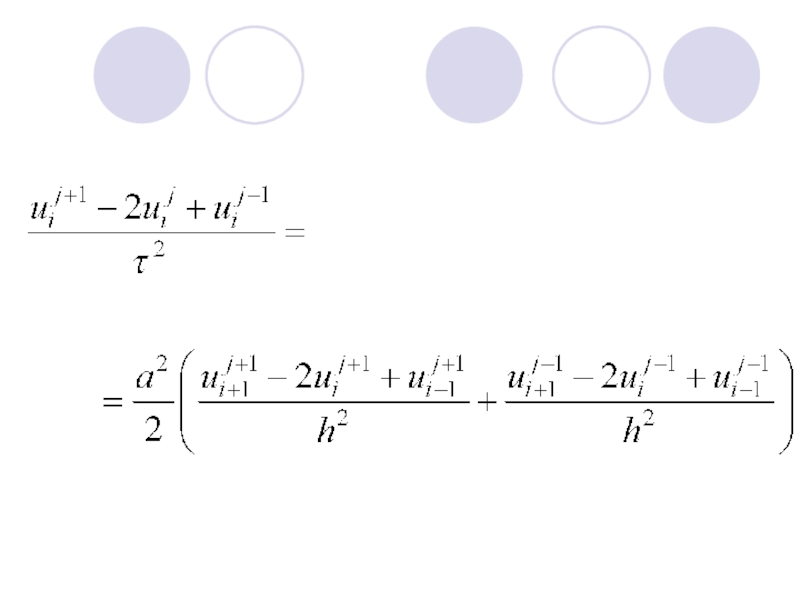
Построим неявную схему.
Вторую производную по t в уравнении аппроксимируем, как
и ранее, по трехточечному шаблону с помощью значений сеточной функции на слоях j - 1, j, j + 1.
Слайд 15Из этого соотношения можно получить систему уравнений относительно неизвестных значений сеточной
функции на (j + 1)-м слое:
Слайд 16ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Интегральным уравнением называется уравнение, неизвестная функция в котором содержится
под знаком интеграла.
В общем случае интегральное уравнение имеет вид
В общем случае интегральное уравнение имеет вид
Слайд 17Виды интегральных уравнений.
Уравнения, в которые искомая функция входит линейно, называются
линейными интегральными уравнениями.
Слайд 18Одним из них является уравнение Фредгольма первого рода
Уравнение Фредгольма второго
рода имеет вид
Слайд 20
Для решения линейных интегральных уравнений строится итерационный процесс, аналогичный методу простой
итерации для нелинейного уравнения.