- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Цифровые автоматические системы и математический аппарат их исследования презентация
Содержание
- 1. Цифровые автоматические системы и математический аппарат их исследования
- 2. Литература Бесекерский В.А., Цифровые автоматические системы, М.:
- 3. Содержание КР Введение Преобразование структурной схемы ЦСАУ
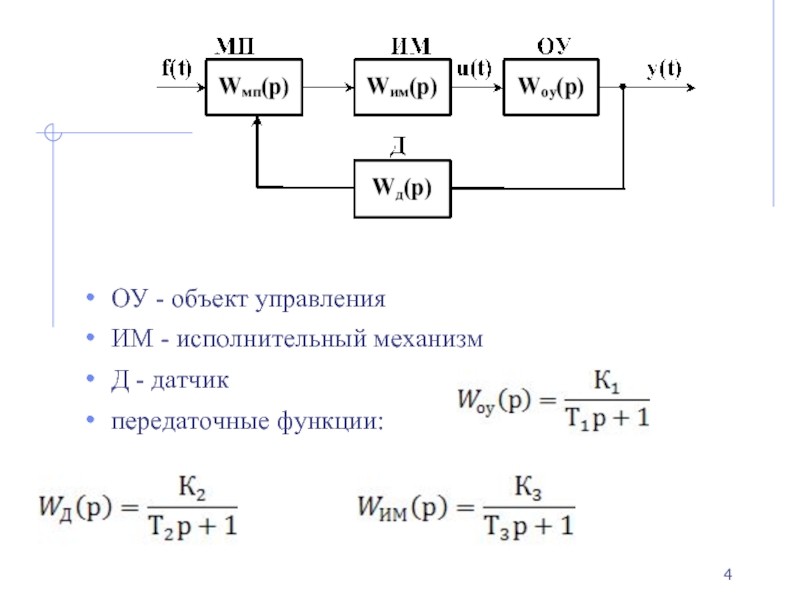
- 4. ОУ - объект управления ИМ - исполнительный
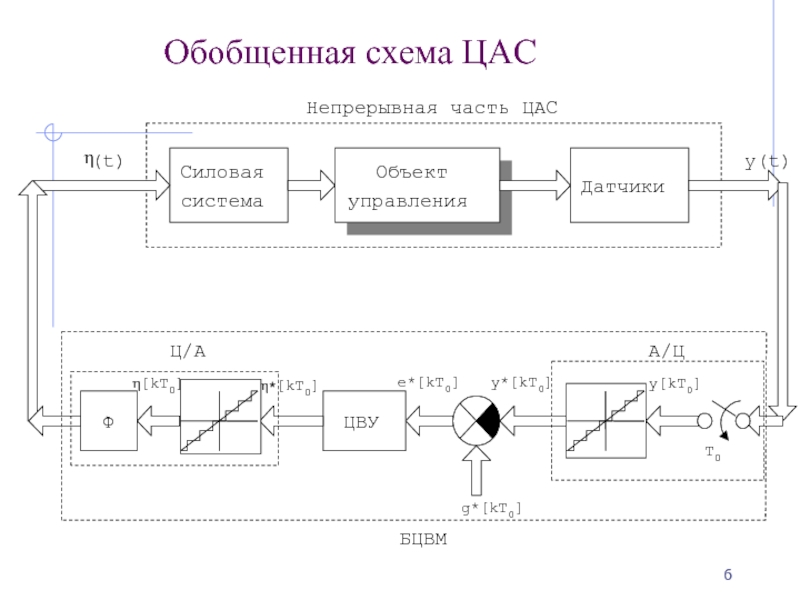
- 6. Обобщенная схема ЦАС
- 7. Цифровое вычислительное устройство Если периоды Т0i повторения
- 8. Особенности цифровых систем Достоинства реализация сложных нелинейные
- 9. Методы исследования цифровых систем 1) методы, основанные
- 10. ПРЕОБРАЗОВАНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ В ЦИФРОВОЙ КОД.
- 11. Квантование по времени – фиксация мгновенных
- 12. Виды модуляции амплитудно-импульсная модуляция — варьируется высота
- 13. Квантование по уровню – замена в
- 14. При одновременном квантовании по времени и уровню
- 15. Преобразование цифрового кода в непрерывный сигнал
- 16. Решетчатая функция – это функция,
- 17. Исследование динамики дискретных систем с использованием переменных
- 18. Преобразование Лапласа каждой преобразуемой по Лапласу функции
- 19. Дискретное преобразование Лапласа p = c+jω;
- 20. Взаимосвязь F*(p) и F(p) Si –
- 21. Z- преобразование результат применения к оригиналу
- 22. Свойства Z- преобразования самостоятельно
Слайд 1ЦИФРОВЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ И МАТЕМАТИЧЕСКИЙ АППАРАТ ИХ ИССЛЕДОВАНИЯ
Цифровые системы автоматического управления
Слайд 2Литература
Бесекерский В.А., Цифровые автоматические системы, М.: Наука, 1976.
Микропроцессорные системы автоматического управления
Структура курса
Лекции -16 часов
Практические занятия- 16 часов
Лабораторные занятия – 16 часов
Экзамен
Курсовая работа
Количество практических и лабораторных работ - 7 шт
Слайд 3Содержание КР
Введение
Преобразование структурной схемы ЦСАУ
Анализ устойчивости ЦСАУ
Анализ переходных процессов ЦСАУ
Анализ ЛАЧХ
Построение
Расчет корректирующего устройства
Заключение
Сроки выполнения КР
30% – 1-2п. – 01.03
60% – 3-4п. – 09.03
90% – 5-6п. – 15.03
Сдача готовой КР – 22.03 – 30.03
Защита КР – 29.03 – 06.04
Балл за КР – 100.
За невыполнение сроков (за каждый раздел) на 1 неделю «-10»
За невыполнение сроков (за каждый раздел) на 2 недели «-20»
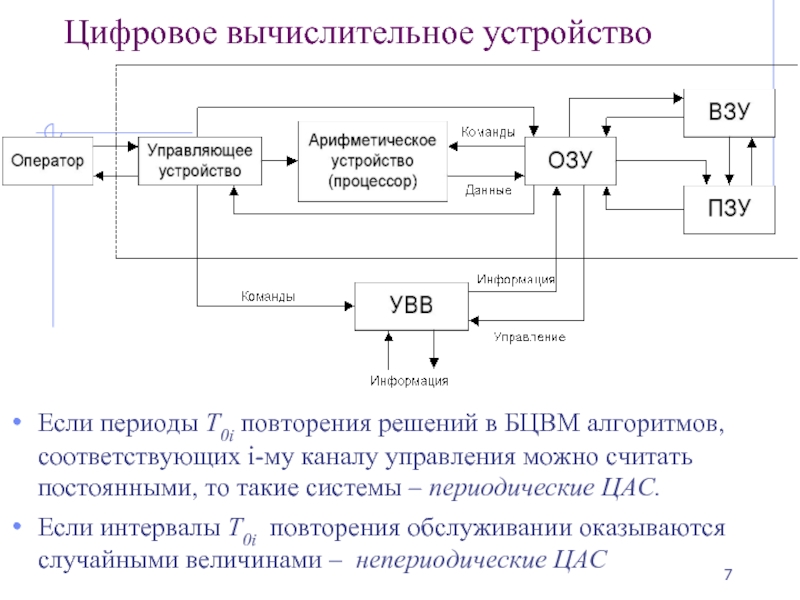
Слайд 7Цифровое вычислительное устройство
Если периоды Т0i повторения решений в БЦВМ алгоритмов, соответствующих
Если интервалы T0i повторения обслуживании оказываются случайными величинами – непериодические ЦАС
Слайд 8Особенности цифровых систем
Достоинства
реализация сложных нелинейные алгоритмов управления, оптимизирующих работу системы по
получение информации, необходимой для построения высокоточных, быстродействующих и надежных автоматических систем;
гибкость, простота перестройки алгоритма управления.
Недостатки
между моментами квантования система фактически не управляется, это может привести к потере устойчивости;
возникновение нежелательных побочных эффектов;
Дискретизация сигналов приводит к появлению явлений, которые не могут возникнуть в непрерывных системах.
Слайд 9Методы исследования цифровых систем
1) методы, основанные на приближенном сведении цифровой системы
2) методы, которые сводятся к исследованию дискретной модели цифровой системы, при этом рассматриваются только значения сигналов в моменты квантования и игнорируются все процессы между этими моментами;
3) точные методы исследования, при которых цифровая система рассматривается в непрерывном времени без каких-либо упрощений и аппроксимаций.
Слайд 10ПРЕОБРАЗОВАНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ В ЦИФРОВОЙ КОД.
КВАНТОВАНИЕ ПО ВРЕМЕНИ И УРОВНЮ
Этапы
квантование по времени,
квантование по уровню
кодирование.
Слайд 11Квантование по времени –
фиксация мгновенных значений непрерывно изменяющейся функции y(t)
Параметры немодулированной последовательности импульсов:
А – высота или амплитуда импульса,
γT0 – длительность или ширина импульса
T0 – расстояние между импульсами или период повторения
y(t), определяющая закон модуляции, называется модулирующей величиной
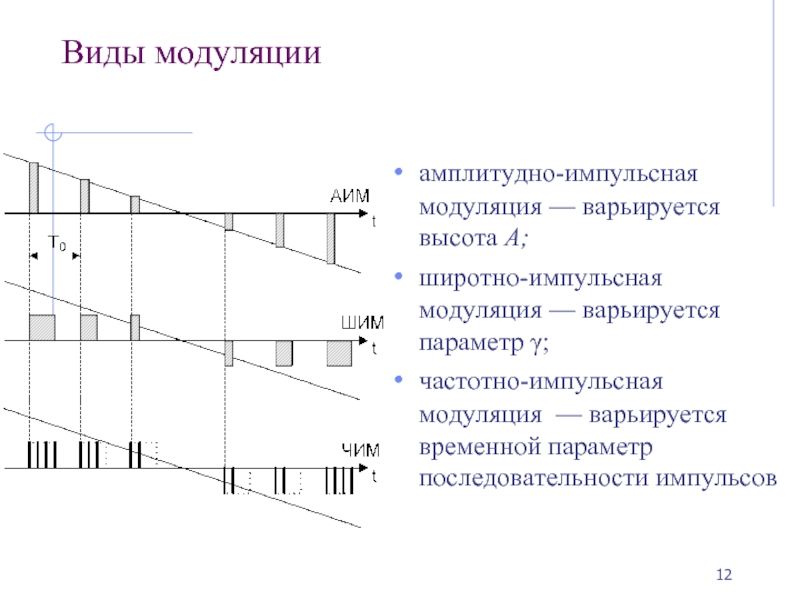
Слайд 12Виды модуляции
амплитудно-импульсная модуляция — варьируется высота А;
широтно-импульсная модуляция — варьируется параметр
частотно-импульсная модуляция — варьируется временной параметр последовательности импульсов
Слайд 13Квантование по уровню –
замена в соответствующие моменты времени мгновенных значений
Число уровней однозначно связано с числом двоичных разрядов преобразователя А/Ц
.
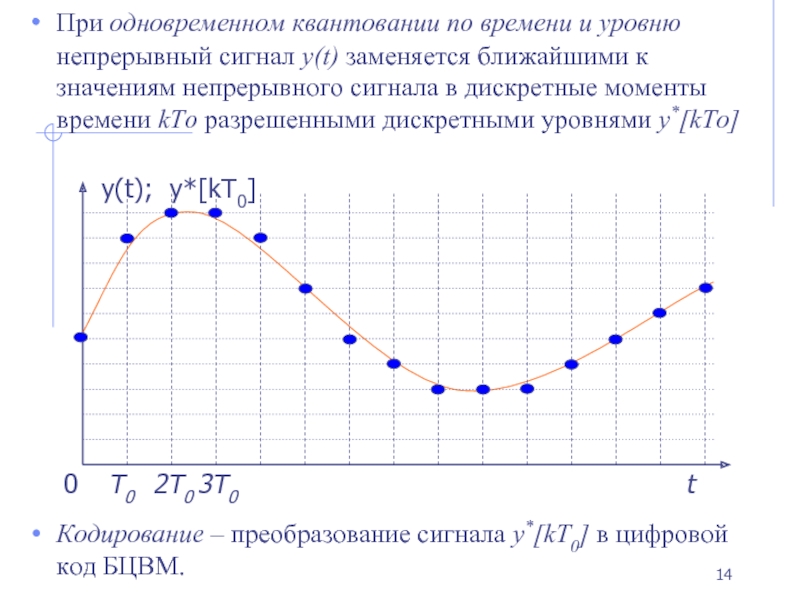
Слайд 14При одновременном квантовании по времени и уровню непрерывный сигнал y(t) заменяется
Кодирование – преобразование сигнала y*[kT0] в цифровой код БЦВМ.
y(t); y*[kT0]
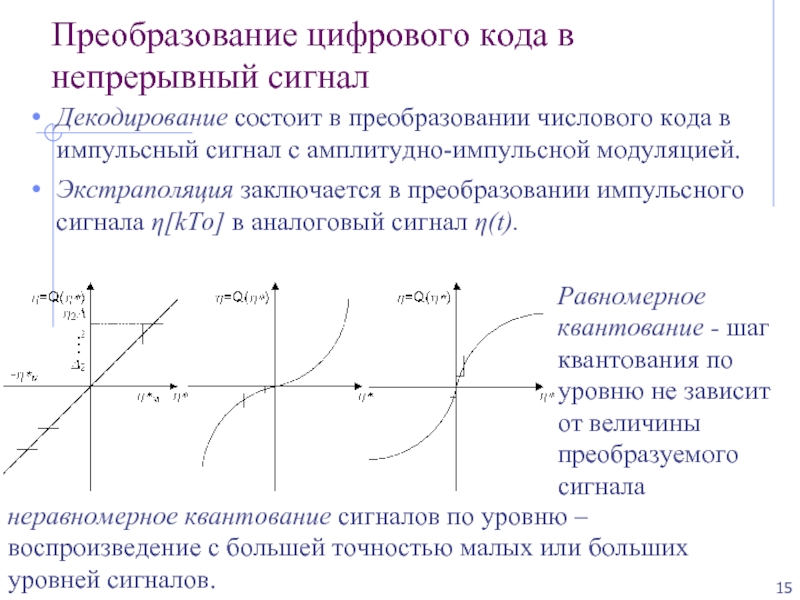
Слайд 15Преобразование цифрового кода в непрерывный сигнал
Декодирование состоит в преобразовании числового
Экстраполяция заключается в преобразовании импульсного сигнала η[kTo] в аналоговый сигнал η(t).
Равномерное квантование - шаг квантования по уровню не зависит от величины преобразуемого сигнала
неравномерное квантование сигналов по уровню – воспроизведение с большей точностью малых или больших уровней сигналов.
Слайд 16 Решетчатая функция –
это функция, значения которой определены лишь в
f [kT] = f(t); t=kT , k=0, 1, 2 ...,
Смещенная решетчатая функция
это функция, значения которой определены для смещенных моментов времени
f [kT, εТ ] = f(t); t=kT+εТ , k=0, 1, 2 ...; 0≤⎜ε⎜•1.
преобразование однозначно ⇒
⇐ преобразование неоднозначно
Слайд 17Исследование динамики дискретных систем
с использованием переменных состояния
Исследование проводят во временной области
Рассматривают
Анализируют свойства ее решений.
Позволяют
рассматривать нелинейные многомерные дискретные системы
проводить исследование их свойств
решать задачи синтеза
с использованием входных и выходных переменных системы
Исследуют поведение некоторых величин, по изменению которых и оценивается качество САУ – выходных переменных системы
Позволяют
проводить анализ зависимости выходных переменных от входных величин,
определять, как придать системе требуемые свойства по этим переменным.
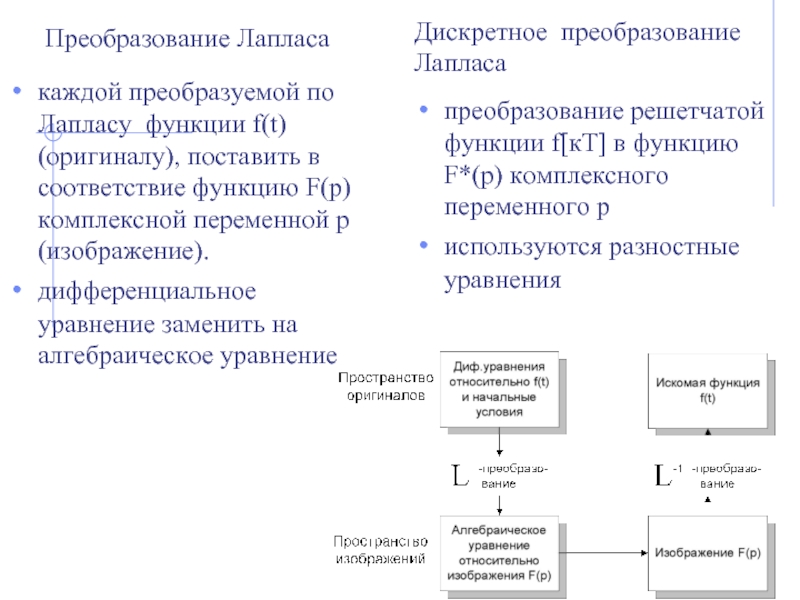
Слайд 18Преобразование Лапласа
каждой преобразуемой по Лапласу функции f(t) (оригиналу), поставить в соответствие
дифференциальное уравнение заменить на алгебраическое уравнение
Дискретное преобразование Лапласа
преобразование решетчатой функции f[кТ] в функцию F*(p) комплексного переменного р
используются разностные уравнения
Слайд 19Дискретное преобразование Лапласа
p = c+jω;
f [kT]- решетчатая функция (оригинал
F*(p)-изображение.
Для смещенной решетчатой функции f [k,ε]
Слайд 20Взаимосвязь F*(p) и F(p)
Si – полюсы изображения
Для смещенного оригинала
Z-преобразование
z=epT
Для смещенной решетчатой функции - модифицированное Z-преобразование.
Слайд 21Z- преобразование
результат применения к оригиналу f[kT] или изображению F(p), D
Z-преобразование несмещенной функции
Z-преобразование смещенной функции










![Дискретное преобразование Лапласа p = c+jω; f [kT]- решетчатая функция (оригинал ); F*(p)-изображение.Для смещенной решетчатой](/img/tmb/3/205998/cd1ce319edd90e6118ed80b3857cdbe3-800x.jpg)

![Z- преобразование результат применения к оригиналу f[kT] или изображению F(p), D или преобразования с](/img/tmb/3/205998/0566af5b8762b5eb5bd76c228709eb89-800x.jpg)






