- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ презентация
Содержание
- 1. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
- 2. Содержание Центральная симметрия Задачи Построение Центральная симметрия в окружающем мире Заключение
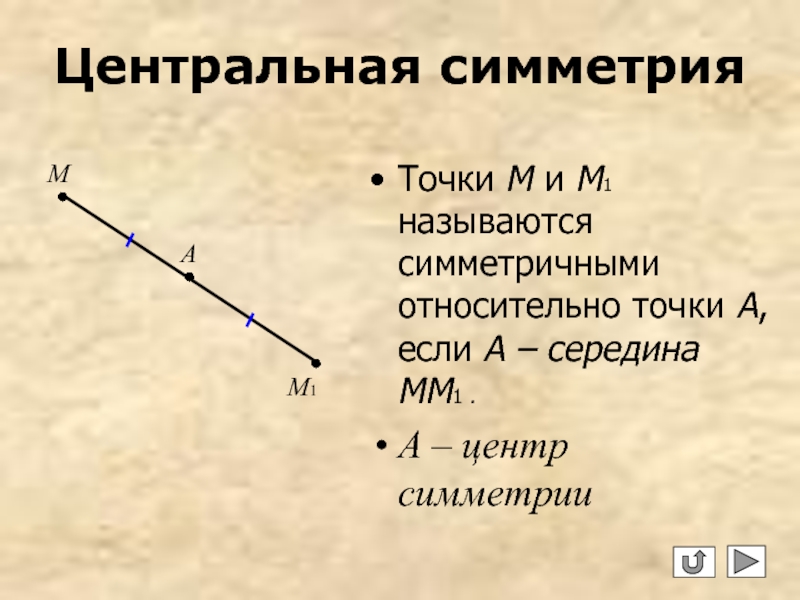
- 3. Центральная симметрия Точки М и М1 называются
- 4. Фигура называется симметричной относительно центра симметрии, если
- 5. Центральная симметрия
- 6. Фигуры, обладающие центром симметрии
- 7. Фигуры,не обладающие центральной симметрией Неправильный многоугольник Произвольный треугольник Угол трапеция
- 8. Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному
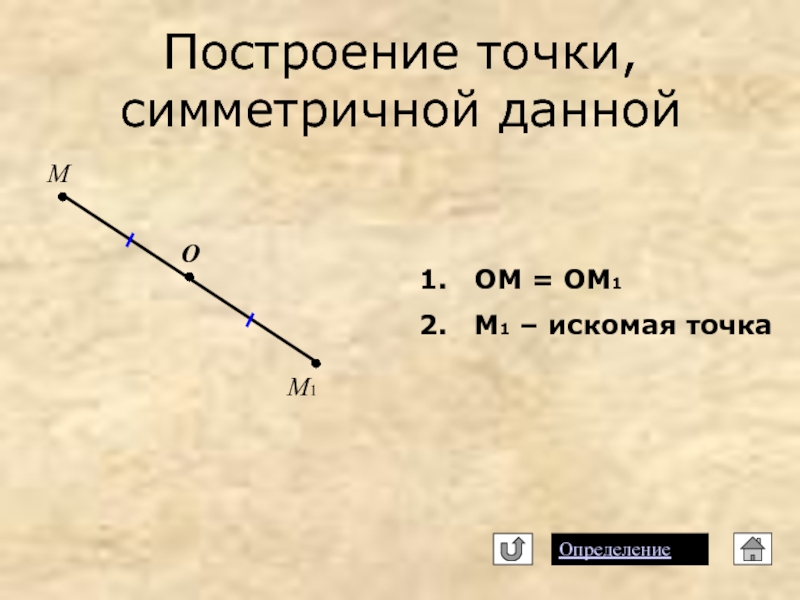
- 9. Построение точки, симметричной данной Определение
- 10. Построение отрезка, симметричного данному Определение
- 11. Построение треугольника, симметричного данному Определение
- 12. Задачи 1. Отрезок АВ, перпендикулярный прямой
- 13. 5. Для каждого из случаев, представленных
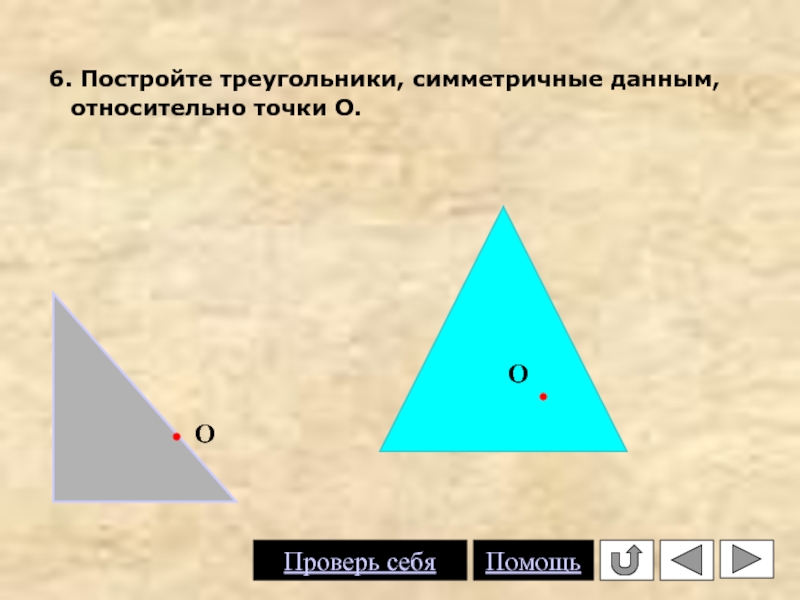
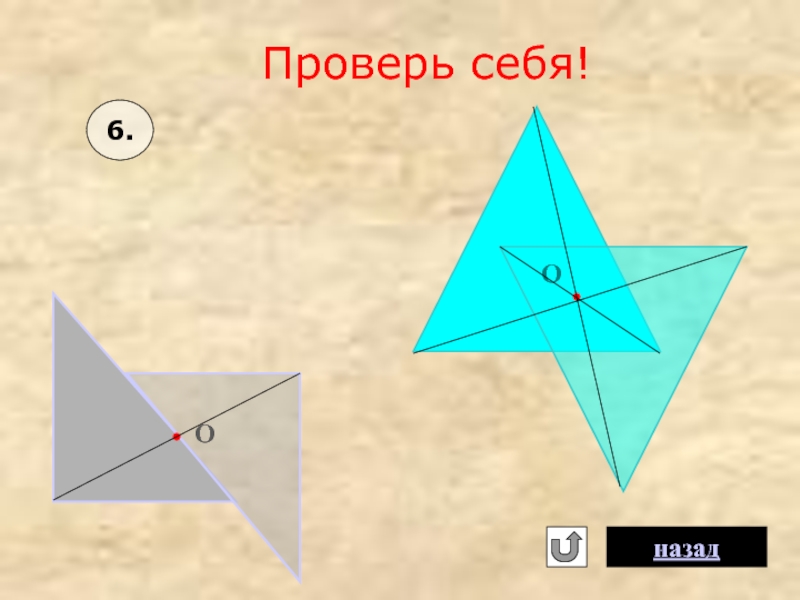
- 14. 6. Постройте треугольники, симметричные данным, относительно
- 15. 7. Постройте произвольный треугольник и его
- 16. Проверь себя! 1. Нет, т.к. по
- 17. Проверь себя! О
- 18. Проверь себя! В А О
- 19. Проверь себя! О О назад 6.
- 20. Проверь себя!
- 21. Заключение Симметрию можно обнаружить почти везде, если
Слайд 2Содержание
Центральная симметрия
Задачи
Построение
Центральная симметрия в окружающем мире
Заключение
Слайд 3Центральная симметрия
Точки М и М1 называются симметричными относительно точки А, если
A – центр симметрии
A
M
M1
Слайд 4Фигура называется симметричной относительно центра симметрии, если для каждой точки фигуры
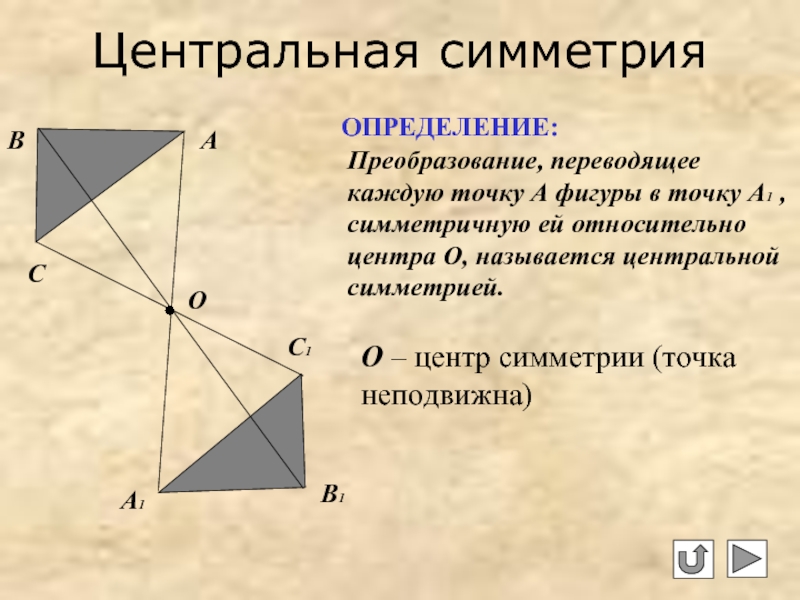
Слайд 5Центральная симметрия
Преобразование, переводящее каждую точку А фигуры в точку А1 ,
ОПРЕДЕЛЕНИЕ:
О
О – центр симметрии (точка неподвижна)
А
А1
B
B1
C
C1
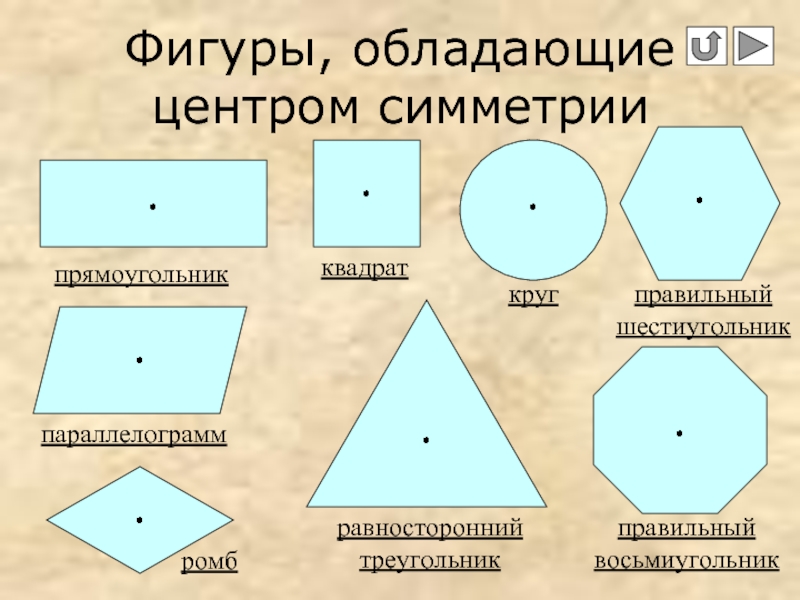
Слайд 6Фигуры, обладающие центром симметрии
прямоугольник
квадрат
круг
правильный шестиугольник
параллелограмм
ромб
равносторонний треугольник
правильный восьмиугольник
Слайд 7Фигуры,не обладающие центральной симметрией
Неправильный многоугольник
Произвольный треугольник
Угол
трапеция
Слайд 8Построение
точки, симметричной данной
отрезка, симметричного данному
треугольника, симметричного данному
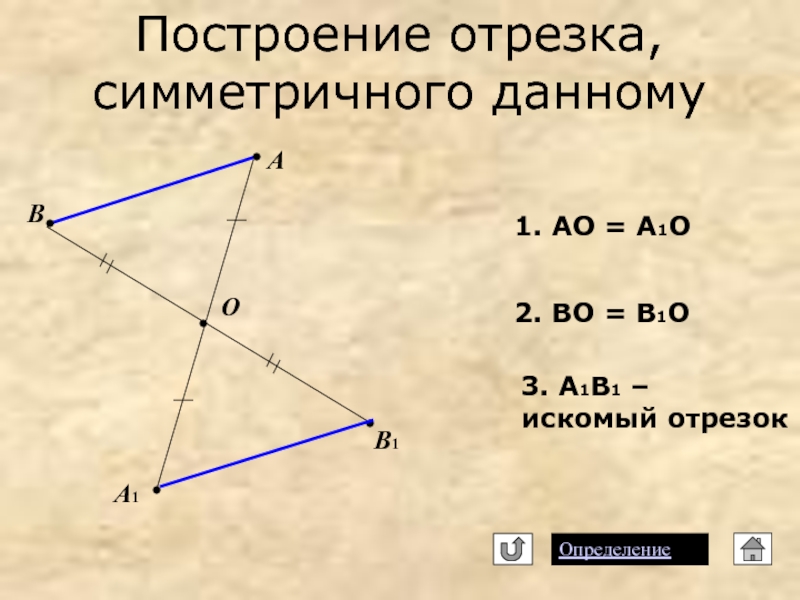
Слайд 10Построение отрезка, симметричного данному
Определение
А
А1
О
B
B1
1. АО = А1О
2. ВО = В1О
3. А1В1
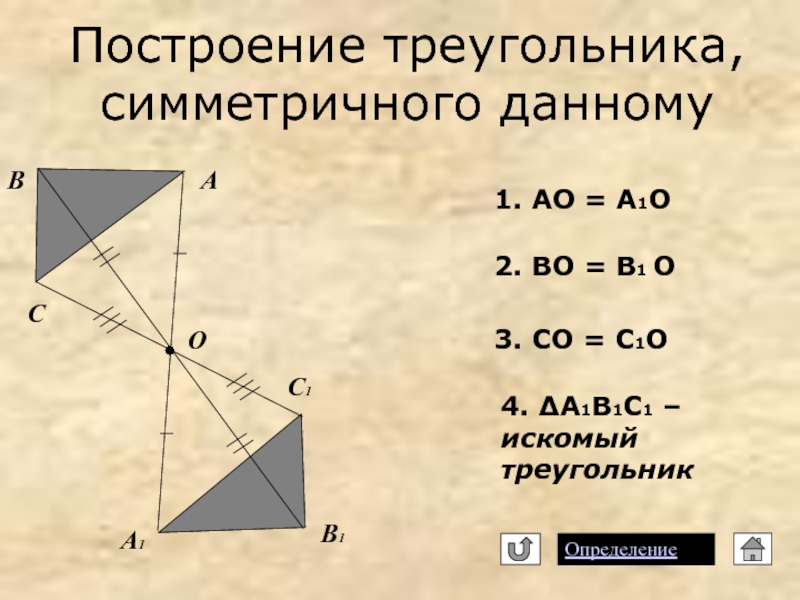
Слайд 11Построение треугольника, симметричного данному
Определение
О
А
А1
B
B1
C
C1
2. ВО = В1 О
1. АО =
3. СО = С1О
4. ΔА1В1С1 – искомый треугольник
Слайд 12Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О
2. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
А
В
С
О
3. Постройте угол, симметричный углу ABC относительно центра О.
Проверь себя
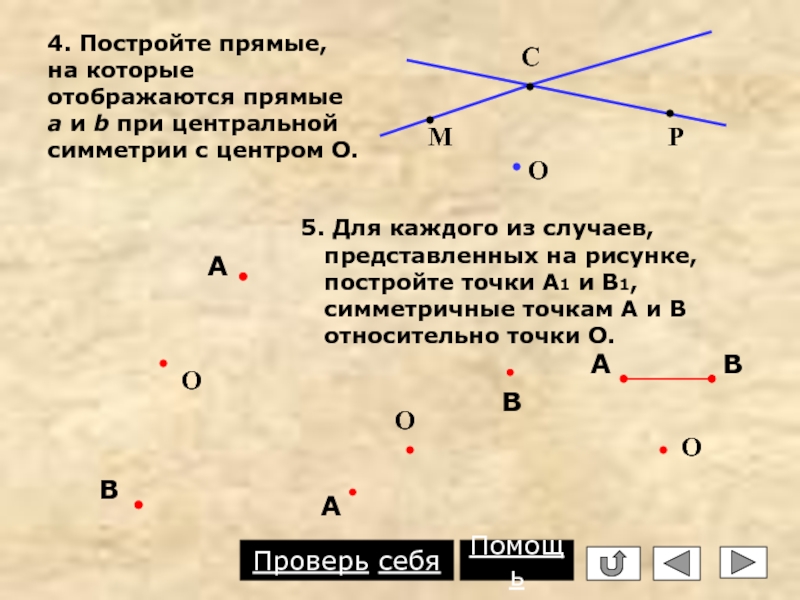
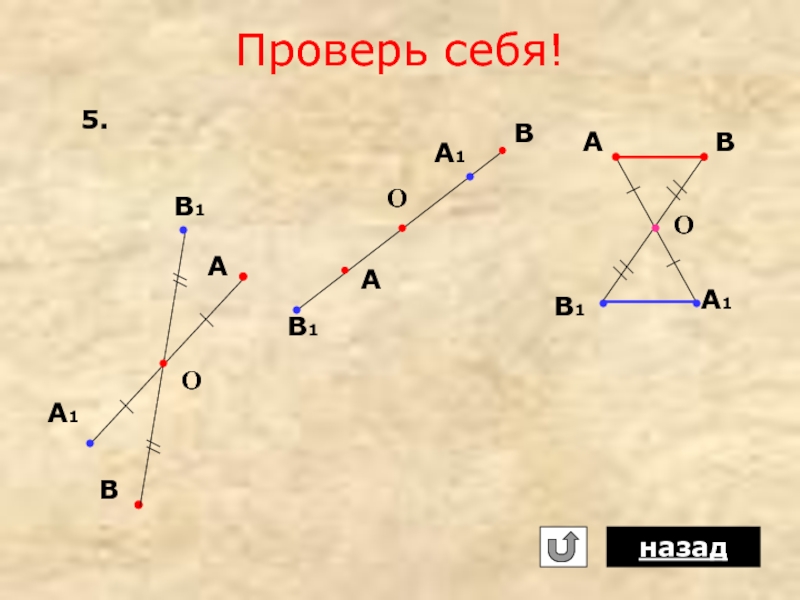
Слайд 13 5. Для каждого из случаев, представленных на рисунке, постройте точки
В
А
А
В
А
В
О
О
О
О
С
М
Р
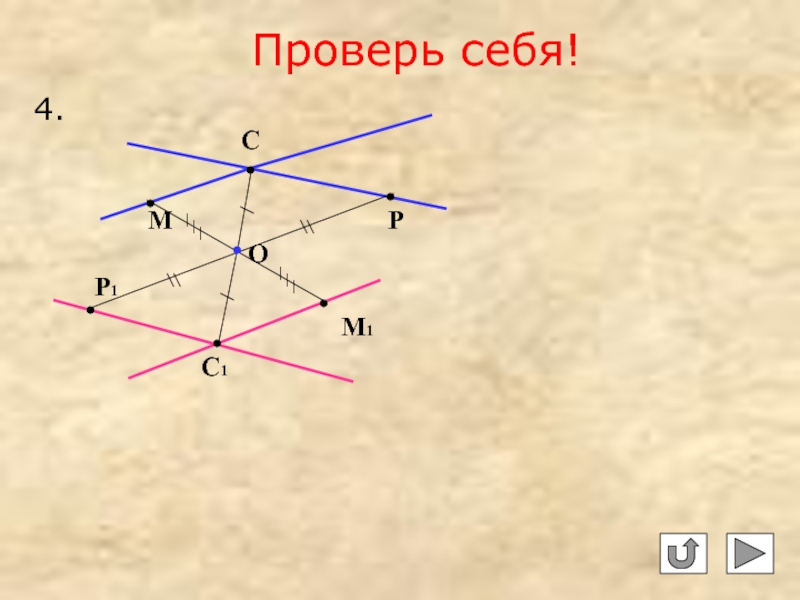
4. Постройте прямые, на которые отображаются прямые a и b при центральной симметрии с центром О.
Проверь себя
Помощь
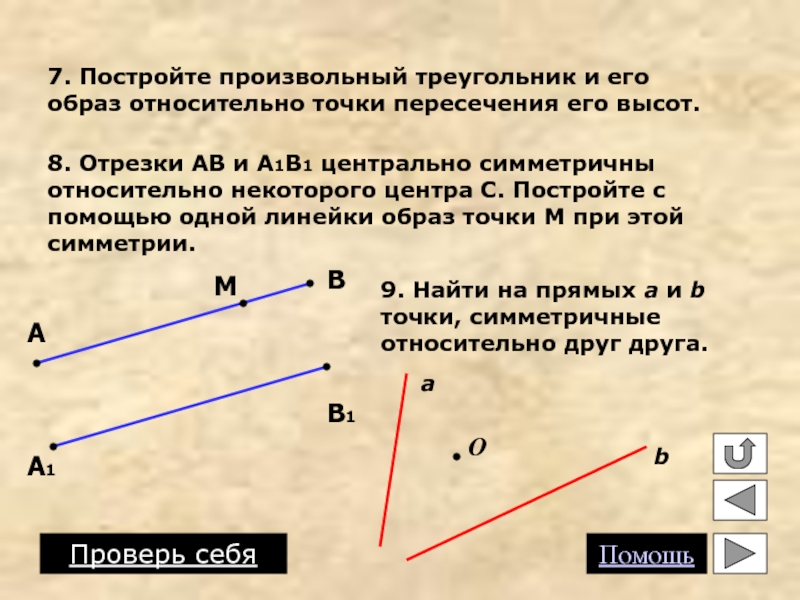
Слайд 157. Постройте произвольный треугольник и его образ относительно точки пересечения
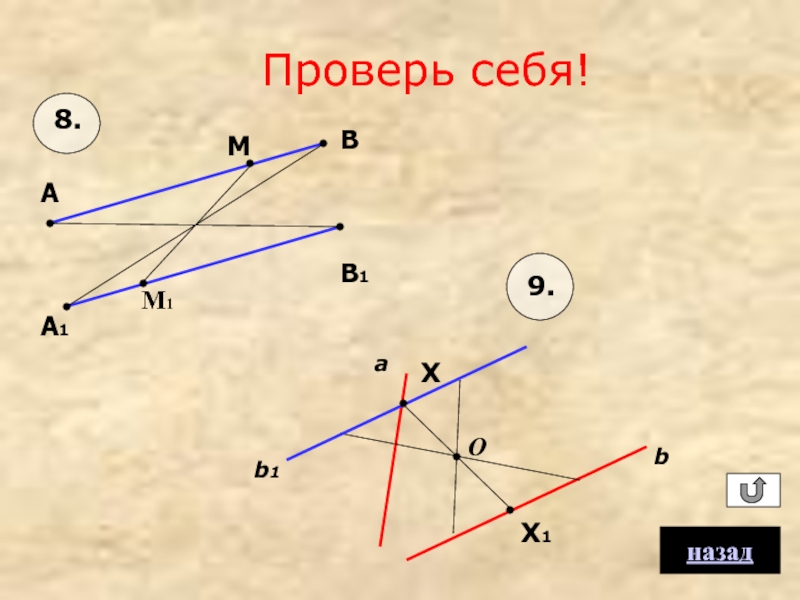
8. Отрезки АВ и А1В1 центрально симметричны относительно некоторого центра С. Постройте с помощью одной линейки образ точки М при этой симметрии.
А
В
А1
В1
М
9. Найти на прямых a и b точки, симметричные относительно друг друга.
a
b
O
Проверь себя
Помощь
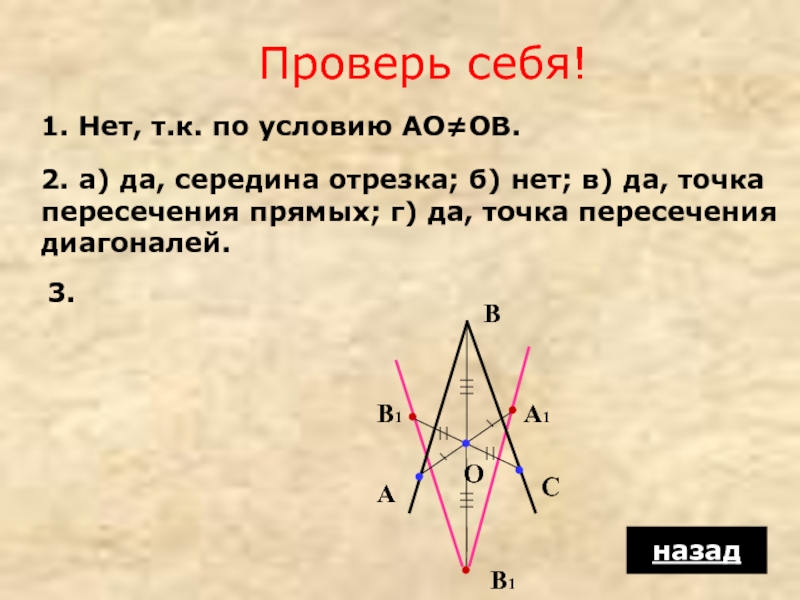
Слайд 16Проверь себя!
1. Нет, т.к. по условию АО≠ОВ.
2. а) да, середина отрезка;
3.
А
В
С
О
В1
А1
В1
назад
Слайд 21Заключение
Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие